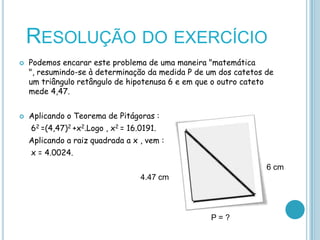
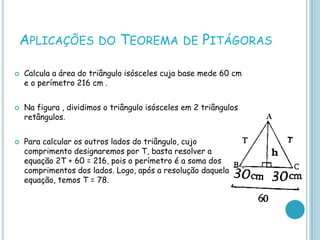
Pitágoras foi um filósofo e matemático grego que viveu entre os séculos VI-V a.C. e fundou uma escola em Crotona. Ele é conhecido por seu teorema sobre triângulos retângulos, que relaciona os lados da hipotenusa e dos catetos. O documento apresenta detalhes sobre a vida e obra de Pitágoras e exemplifica a aplicação de seu famoso teorema em problemas geométricos.

2. PITÁGORAS
 Nome completo: Ὁ Πσθαγόρας
 Data de nascimento: 580 a. C. - 572 a. C, na cidade de Samos.
 Data de falecimento: 500 a. C. - 490 a. C.
 Principais interesses:
Metafisica, Música, Matemática, Ética, Política Astronomia.
 Fundou uma escola mística e filosófica em Crotona (colônias
gregas na península itálica), cujos princípios foram determinantes
para a evolução geral da matemática e da filosofia ocidental
sendo os principais temas a harmonia matemática, a doutrina dos
números e o dualismo cósmico essencial.

3. TEOREMA DE PITÁGORAS
 Em qualquer triângulo retângulo, o quadrado do comprimento da
hipotenusa é igual à soma dos quadrados dos comprimentos dos
catetos.”Por definição, a hipotenusa é o lado oposto ao ângulo
reto, e os catetos são os dois lados que o formam.
 Em qualquer triângulo retângulo, a área do quadrado cujo lado é a
hipotenusa é igual à soma das áreas dos quadrados cujos lados são
os catetos.

4. APLICAÇÕES DO TEOREMA DE
PITÁGORAS
 1.Uma escada com 6 metros de comprimento, está encostada a
um muro com 4,47 metros de altura, de modo que uma das
extremidades da escada encostada à parte de cima do muro.
 Qual a distância da escada ao muro, medida sobre o chão?

5. RESOLUÇÃO DO EXERCÍCIO
 Podemos encarar este problema de uma maneira "matemática
", resumindo-se à determinação da medida P de um dos catetos de
um triângulo retângulo de hipotenusa 6 e em que o outro cateto
mede 4,47.
 Aplicando o Teorema de Pitágoras :
62 =(4,47)2 +x2.Logo , x2 = 16.0191.
Aplicando a raiz quadrada a x , vem :
x = 4.0024.
6 cm
4.47 cm
P=?

6. APLICAÇÕES DO TEOREMA DE PITÁGORAS
 Calcula a área do triângulo isósceles cuja base mede 60 cm
e o perímetro 216 cm .
 Na figura , dividimos o triângulo isósceles em 2 triângulos
retângulos.
 Para calcular os outros lados do triângulo, cujo
comprimento designaremos por T, basta resolver a
equação 2T + 60 = 216, pois o perímetro é a soma dos
comprimentos dos lados. Logo, após a resolução daquela
equação, temos T = 78.

7. CONTINUAÇÃO DA RESPOSTA
 Conhecidos os comprimentos dos lados iguais, vamos
determinar a altura, que designaremos por h.
 Aplicando o Teorema de Pitágoras no triângulo vem :
(78)2 = (30)2 + h2 de onde , h=72.
 Há agora que determinar a área de triângulo.
Conhecemos o comprimento da base e a altura e
como a área se calcula multiplicando a base pela
altura e dividindo por dois , temos A= (60 x 72)/2
=2160 cm 2.