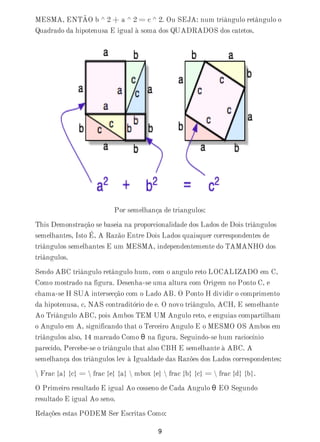
Este documento apresenta um resumo sobre o teorema de Pitágoras, incluindo sua história, demonstrações e aplicações. O autor é Linoel Batista Lanhoso, licenciado em matemática, e o documento contém 12 páginas sobre o teorema, como quem foi Pitágoras, formas de demonstrar a relação matemática e exemplos práticos de sua aplicação.

2. 3
4
5
6
7
Índice Remissivo
Sobre o Livro
Sobre o Autor
DIREITOS Autorais
Prefácio
O teorema de Pit
2

3. Sobre o Livro
Este livro tem como objetivo divulgar um pouco da história do famoso teorema de
Pitágoras, algumas aplicações e exeplos.....
Boa Leitura...
3

4. Sobre o Autor
[Linoel Batista Lanhos] Licenciado em Matemática (UEPG/2012), atualmente
tutor presencial no Polo UAB de Reserva-PR.
4

5. Copirraite
Autor
[Linoel Batista Lanhoso]
Editor
[Linoel Batista Lanhoso]
Copirraite © 2013 [ Linoel Batista Lanhoso]
Primeira Publicação usando Papyrus de 2013
ISBN: [Insira ISBN here]
Este Livro PODE Ser Educação adquirido POR, Negócios, vendas OU USO
promocional. Edição on-line also available ESTÁ parágrafo este título.
INFORMAÇÕES MAIS Pará, contacte O Nosso departamento de vendas
Corporativas / Institucionais: [Insira o Seu Número de telefone here] ou [Insira
Seu e-mail here]
Embora Toda precaução tenha Sido Tomada na PREPARACAO Deste Livro, a
editora e Os Autores NÃO assumem nenhuma Responsabilidade POR Erros UO
omissões, OU POR Danos resultantes da utilização das INFORMAÇÕES here
contidas.
5

6. Prefácio
Quem foi Pitágoras?
Onde viveu?
Perguntas como essas são uma introdução a esse tão usado teorema...
Pitágoras de Samos foi hum filósofo e matemático grego. Da vida de
Pitágoras Quase nada PODE Ser afirmado com certeza, JA Que ELE foi Objeto
de Uma série de relatos tardios e fantasiosos, Como OS referentes a Viagens e
contatos com Culturas Orientais Como. Parece Certo , contudo, que o filósofo tenha
Nascido em 570 aC Na cidade de Samos. Fundou UMA Escola Mística e
Filosófica EM Crotona (Colonias Gregas de na península Itálica), cujos Princípios
were Determinantes Pará Uma Evolução Geral da matemática e da filosofia
Ocidental, podendo Sendo OS principais temas a harmonia matemática, a
Doutrina dos Números EO dualismo Cósmico essencial. Acredita-se that
Pitágoras tenha Sido casado com Uma física e matemática grega Theano, that foi
aluna SUA. Supõe-se that Ela e As Duas Filhas tenham assumido Uma escola
pitagórica Apos Uma morte Fazer Marido.
6

7. O teorema de Pitágoras.
O é um Teorema?
Na matemática, um teorema E UMA Afirmação that PODE Ser provada Como
Verdadeira atraves de Otras afirmações Já demonstradas, página Outros Como
teoremas, juntamente com afirmações anteriormente aceitas, Como axiomas.
Prova E o Processo de Mostrar Que hum teorema ESTÁ Correto. O termo foi
introduzido teorema POR Euclides, em Elementos, parágrafo significar
"Afirmação that PODE Ser provada". Em grego, originalmente significava
"espetáculo" ou "festa". Atualmente, e Mais Comum deixar o termo "teorema"
Apenas para Certas afirmações that PODEM Ser provadas e de grande
"matemática importancia", O Que Torna a Definição hum tanto subjetiva.
È importante Notar que "teorema" E diferente de "Teoria".
O teorema de Pitágoras....
O teorema de Pitágoras: a soma das áreas dos QUADRADOS construidos Sobre
os catetos (AEB) equivale à área do Quadrado construido Sobre a hipotenusa (c).
Em QUALQUÉR triângulo retângulo, o Quadrado do comprimento da hipotenusa
E igual à soma dos QUADRADOS dos comprimentos dos catetos.
7

8. Demostrações:
Muitas são as demostrações do Teorema de Pitágoras...Vamos a algumas
Por comparação de áreas
Desenha-se um Quadrado de Lado b + a;
De um Modo de este subdividir Quadrado EM retângulos Quatro, Sendo Dois
DELES QUADRADOS de Lados, respectively, aeb: Traça-se Dois Segmentos de
reta Paralelos A Dois Lados consecutivos do Quadrado, Sendo Cada hum DELES
interno ao Quadrado e com o MESMO comprimento that o lado do Quadrado;
Divide-se Cada hum destes Dois retângulos em Dois triângulos retângulos,
traçando-se como diagonais. Chama-se co comprimento de Cada diagonal;
A área da Região Que resta Ao retirar-se triângulos retângulos Os Quatro E igual
ab ^ 2 + a ^ 2;
Desenha-se ágora o MESMO Quadrado de Lado b + a, mas coloca-se triângulos
retângulos Os Quatro noutra posição Dentro do Quadrado: a posição that Deixa
Desocupada Uma Região Que É UM Quadrado de Lado C.
ASSIM, uma área da Região formada when Os Quatro triângulos retângulos São
retirados E igual ac ^ 2.
Como b ^ 2 + a ^ 2 representação de uma área do Quadrado Maior subtraída de
da soma das áreas de dos triângulos retângulos, ec ^ 2 representação de uma área
8

9. MESMA, ENTÃO b ^ 2 + a ^ 2 = c ^ 2. Ou SEJA: num triângulo retângulo o
Quadrado da hipotenusa E igual à soma dos QUADRADOS dos catetos.
Por semelhança de triangulos:
This Demonstração se baseia na proporcionalidade dos Lados de Dois triângulos
semelhantes, Isto É, A Razão Entre Dois Lados quaisquer correspondentes de
triângulos semelhantes E um MESMA, independentemente do TAMANHO dos
triângulos.
Sendo ABC triângulo retângulo hum, com o angulo reto LOCALIZADO em C,
Como mostrado na figura. Desenha-se uma altura com Origem no Ponto C, e
chama-se H SUA intersecção com o Lado AB. O Ponto H dividir o comprimento
da hipotenusa, c, NAS contraditório de e. O novo triângulo, ACH, E semelhante
Ao Triângulo ABC, pois Ambos TEM UM Angulo reto, e enguias compartilham
o Angulo em A, significando that o Terceiro Angulo E o MESMO OS Ambos em
triângulos also, 14 marcado Como θ na figura. Seguindo-se hum raciocínio
parecido, Percebe-se o triângulo that also CBH E semelhante à ABC. A
semelhança dos triângulos lev à Igualdade das Razões dos Lados correspondentes:
Frac {a} {c} = frac {e} {a} mbox {e} frac {b} {c} = frac {d} {b}.
O Primeiro resultado E igual Ao cosseno de Cada Angulo θ EO Segundo
resultado E igual Ao seno.
Relações estas PODEM Ser Escritas Como:
9

10. a ^ 2 = c times e mbox {e} b ^ 2 = c times d.
Somando estas Duas igualdades, obtém-se
a ^ 2 + b ^ 2 = c times e + c times d = c times (D + E) = c ^ 2,
Que, rearranjada, E o teorema de Pitágoras:
a ^ 2 + b = c ^ 2 ^ 2 .
Aplicações e exemplos:
O teorema proposto POR Pitágoras ESTÁ Presente em Situações Diversas
cotidianas. Vamos atraves de Exemplos demonstrar algumas applications.
Exemplo 1
Uma escada Apoiada em Uma Parede TEM SUA distante base de cerca de 6
metros da Parede. Sabendo Que A Parede mede cerca de oito metros, determinar o
comprimento da escada.
10

11. x² = 8² + 6²
x² = 64 + 36
x² = 100
√x² = √100
x = 10
Uma escada POSSUI 10 metros de comprimento.
Exemplo 2
Um terreno retangular como POSSUI seguintes Medidas: 20 metros de
comprimento e 30 metros de Largura. Determinar uma Medida diagonal da Desse
terreno.
A divisão diagonal o retângulo em Dois triângulos retângulos, consistindo na
hipotenusa DELES. Portanto, utilizaremos o Teorema de Pitágoras Para
determinar a Medida da diagonal. Veja:
11

12. d² = 30² + 20²
d² = 900 + 400
d² = 1300
√d² = √1300
d = 36 metros (apróximadamente)
Dentre Muitos outros exemplos e aplicações
espero ter ajudado de alguma forma
...
12