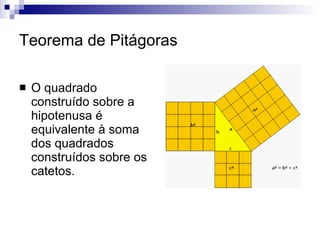
O documento descreve os ternos pitagóricos, que são triplos de números inteiros que satisfazem a equação a2 + b2 = c2, onde c é a hipotenusa e a, b são os catetos de um triângulo retângulo. Explica como encontrar esses ternos e classifica-os em primitivos, quando seus números são primos entre si, e compostos, quando não o são.

1. Ternos Pitagóricos

2. Teorema de Pitágoras O quadrado construído sobre a hipotenusa é equivalente à soma dos quadrados construídos sobre os catetos.

3. Sabe-se que o Teorema de Pitágoras não é válido apenas para o quadrado; é válido para três polígonos semelhantes cujos lados homólogos a , b e c , sejam de um triângulo retângulo.

4. A figura mostra o Teorema de Pitágoras aplicado ao triângulo equilátero: O triângulo equilátero T, construído sobre a hipotenusa, é equivalente à soma dos triângulos equiláteros T’ e T” construídos sobre os catetos.

5. Terno de números pitagóricos Quando três números inteiros a , b e c (não nulos) satisfazem à relação dizemos que esses números formam um terno de números pitagóricos , ou simplesmente, um terno pitagórico .

6. Assim os ternos: são ternos pitagóricos. O quadrado do número maior é igual à soma dos quadrados dos outros dois. 8 15 17 5 12 13 3 4 5

7. Qualquer terno pitagórico será uma solução inteira para a equação diofantina: Na qual x é a hipotenusa e y e z são os catetos de um triângulo retângulo.

8. Como obter os ternos pitagóricos? Basta tomar as expressões: e atribuir aos elementos a e b valores inteiros, positivos e diferentes, sendo a maior do que b . hipotenusa catetos

9. Exemplo : Fazendo a = 5 e b = 2, obtemos o seguinte terno pitagórico: 29 20 21

10. Terno pitagórico primitivo Um terno pitagórico é primitivo quando os elementos que o formam são primos entre si . São ternos pitagóricos primitivos: 9 40 41 8 15 17 5 12 13

11. Ternos compostos ou não-primitivos Os seus elementos não são primos entre si. Se multiplicarmos os elementos de um terno primitivo por um número inteiro m (maior do que 1) vamos obter um terno composto ou não-primitivo.

12. Exemplo : Do terno primitivo tiramos os ternos não-primitivos 36 48 60 9 12 15 6 8 10 3 4 5

13. Dado um terno pitagórico não-primitivo podemos dividir todos os elementos desse terno pelo seu m.d.c. e obtemos um terno pitagórico primitivo .

14. Tomemos por exemplo o terno pitagórico Dividindo-se os três elementos por 12 (m.d.c.), obtemos que é um terno pitagórico primitivo . 144 132 150 12 11 25

15. Acredita-se que uma lista de dois dos três números de um terno pitagórico estão na chamada Tábua de Plimton 332. A Tábua de Plimton 332 é uma tábua de barro de origem babilônica, datada de 1800 a.C., que se encontra na Universidade de Columbia. Fonte:http://www.uch.ceu.es/principal/eponimos_cientificos/pitagoras.asp

16. O terno pitagórico 5 4 3 é o mais notável de todos, pois é formado por três números consecutivos, e, nesse terno, a soma dos elementos é a menor possível. Esse terno define um triângulo retângulo denominado pelos geômetras gregos de “ triângulo nupcial”.

17. Experimente agora encontrar outros ternos pitagórios.

18. Referências Bibliográficas TAHAN, Malba. As maravilhas da Matemática . 6. ed. Rio de Janeiro: Bloch, 1987. TERNA PITAGÓRICA. Disponível em:< http://www.uch.ceu.es/principal/eponimos_cientificos/pitagoras.asp >. Acesso em: 4 dez. 2010.