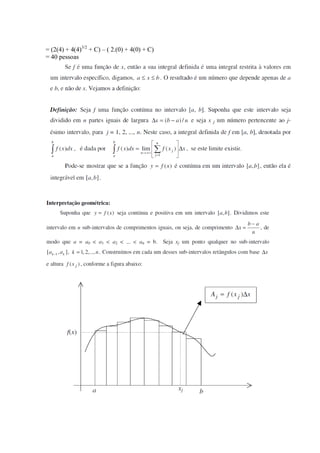
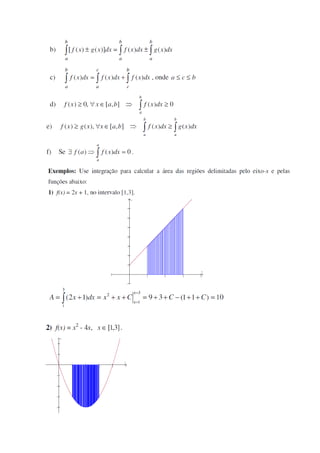
Este documento apresenta um resumo sobre integrais definidas. Explica que a integral definida representa a variação acumulada de uma grandeza entre dois limites e denota a área sob uma curva entre esses limites. Fornece um exemplo para calcular a população acumulada em um período de tempo usando uma integral definida e apresenta exercícios para cálculo de áreas limitadas por curvas.

1. UNIVERSIDAD FERMIN TORO
CABUDARE ESTADO LARA
MATEMATICA II
WILMER SEGOVIA
C.I. 21126413
Integral Definida
Suponha que você conheça a taxa f(x) = dF/dx, na qual uma certa grandeza F
está variando e deseje encontrar a quantidade pela qual a grandeza F variará entre x = a
e x = b. Você pode primeiro encontrar F por antidiferenciação, e então calcular a
diferença:
Variação em F entre
x= a e x = b = F(b) – F(a)
O resultado numérico deste cálculo é chamado de integral definida da função f e
é denotado pelo símbolo:
b
f ( x)dx
a
b
O símbolo f ( x)dx é lido como “ a integral definida de f de a até b”. Os
a
números a e b são denominados limites de integração. Nos cálculos que envolvem as
integrais definidas, é freqüentemente conveniente usar o símbolo:
F ( x) b para a diferença F(b) – F(a).
a
Ex.: Um estudo indica que, daqui a x meses a população de uma cidade estará crescendo
a uma taxa de 2 + 6 x pessoas por mês. Em quanto a população crescerá durante os
próximos 4 meses?
Solução:
P(x) = população daqui a x meses, então a taxa da variação da população em relação ao
tempo dP/dx = 2 + 6 x e a quantidade pela qual a população crescerá durante os
próximos 4 meses será a integral definida:
4
P(4) – P(0) = (2 6 x )dx
0
4 4
=2 dx + 6 ( x 1/2 dx
0 0
3/ 2
6x 4
= 2x + C 0
3/ 2
= 2x + 4x 3 / 2 + C 4
0

2. = (2(4) + 4(4)3/2 + C) – ( 2.(0) + 4(0) + C)
= 40 pessoas

6. Exercícios:
1. Calcular as integrais.
2 0
3
a) x(1 x )dx b) (x 2 4 x 7)dx
1 3
2 1
dx dy
c) d)
1 x6 0 3y 1
3
4 1
x 2 dx
e) senx cosdx f)
1 x3 9
4
3
g) ( x 1 x )dx
0
2. Encontre a área da região limitada pelas curvas y = x2 +1 e y = 2x – 2 entre
x = -1 e x = 2.
3. Encontre a área da região limitada pelas curvas y = x3 e y = x2 .
4. Encontre a área da região limitada pela curva y = -x2 + 4x – 3 e pelo eixo x.
5. Encontre a área da Região R no primeiro quadrante que se situa sob a curva
y = 1/x e é limitado por esta curva e pelas retas y = x, x=0 e x =2.
6. Encontre a área da região S, limitada pela curva y = senx e pelo eixo dos x de 0
até 2π.
7. Encontre a área limitada por y = x2 e y = x+2.
8. Encontre a área limitada pelas curvas y = x2 – 1 e y = x +1. As curvas
interceptam-se nos pontos de abscissa -1 e 2.