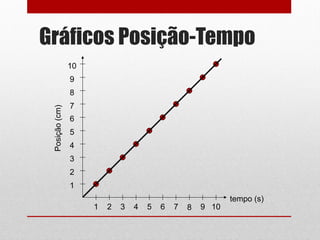
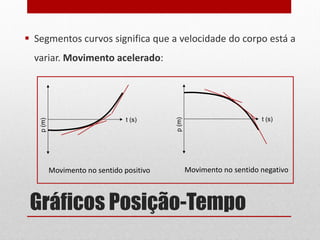
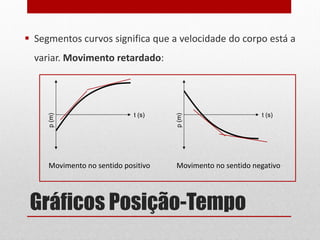
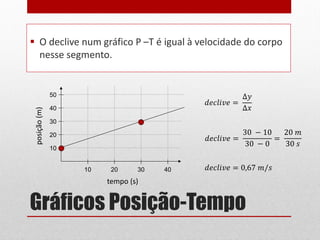
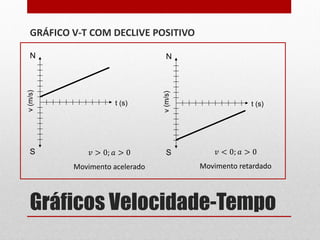
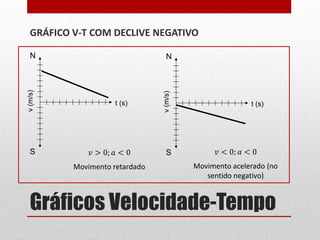
O documento discute gráficos de posição-tempo e velocidade-tempo. Gráficos de posição-tempo mostram a posição de um objeto em relação ao tempo e podem ser usados para identificar diferentes tipos de movimento com base na forma da curva, como movimento uniforme ou acelerado. Gráficos de velocidade-tempo representam a velocidade de um corpo em relação ao tempo e o declive da curva indica se há aceleração ou desaceleração. O documento fornece exemplos de como ler e construir esses tipos

1. Gráficos
 Posição – tempo
 Velocidade - tempo

2. Gráficos Posição-Tempo
GRÁFICOS POSIÇÃO-TEMPO
Mostram a posição de um objeto em função do tempo.
 Eixo do x: tempo (variável independente)
 Eixo do y: posição (variável dependente)

3. Gráficos Posição-Tempo
 Imagine uma bola a rolar ao longo de uma mesa, iluminada
por uma lâmpada estroboscópica a cada segundo.
• Pode-se marcar a posição da bola a cada segundo.
0 s 1 s 2 s 3 s 4 s 5 s 6 s 7 s 8 s 9 s 10 s

4. Gráficos Posição-Tempo
1 2 3 4 5 6 7 8 9 10
1
2
3
4
5
6
7
8
9
10
tempo (s)
Posição(cm)

5. Gráficos Posição-Tempo
 Quais são as características
deste gráfico?
o Linha reta, declive positivo
 Que tipo de movimento se
obteve no gráfico?
o Movimento uniforme 1 2 3 4 5 6 7 8 9 10
1
2
3
4
5
6
7
8
9
10
time (s)
position(cm)

6. Gráficos Posição-tempo
CADA TIPO DE MOVIMENTO TEM UMA REPRESENTAÇÃO
ESPECÍFICA NOS GRÁFICOS POSIÇÃO – TEMPO:
 O movimento uniforme é representado por uma linha reta.
t (s)
p(m)
Movimento em sentido positivo
t (s)
p(m)
Movimento em sentido negativo

7. Gráficos Posição-Tempo
t (s)
p(m)
Um segmento horizontal significa que
o corpo está em repouso

8. Gráficos Posição-Tempo
 Segmentos curvos significa que a velocidade do corpo está a
variar. Movimento acelerado:
t (s)
p(m)
Movimento no sentido positivo
t (s)
p(m)
Movimento no sentido negativo

9. Gráficos Posição-Tempo
 Segmentos curvos significa que a velocidade do corpo está a
variar. Movimento retardado:
t (s)
p(m)
Movimento no sentido positivo
t (s)
p(m)
Movimento no sentido negativo

10. Gráficos Posição-Tempo
 O declive num gráfico P –T é igual à velocidade do corpo
nesse segmento.
tempo (s)
posição(m)
10 20 30 40
10
20
30
40
50
𝑑𝑒𝑐𝑙𝑖𝑣𝑒 =
∆𝑦
∆𝑥
𝑑𝑒𝑐𝑙𝑖𝑣𝑒 =
30 − 10
30 − 0
=
20 𝑚
30 𝑠
𝑑𝑒𝑐𝑙𝑖𝑣𝑒 = 0,67 𝑚/𝑠

11. Gráficos Velocidade-Tempo
Um gráfico velocidade-tempo (V-T) representa a
velocidade de um corpo em função do tempo.
 Linha horizontal = velocidade constante.
Uma linha reta inclinada = aceleração constante.
 Declive positivo = aceleração positiva.
(Nao é necessariamente movimento acelerado!)
 Declive negativo = aceleração negativa.
(Nao é necessariamente movimento retardado!)

12. Gráficos Velocidade-Tempo
Uma linha horizontal num gráfico V-T significa velocidade
constante.
t (s)
v(m/s)
N
S
O corpo está a mover-se
com velocidade
constante a Norte
O corpo está a mover-se
com velocidade
constante a Sul

13. Gráficos Velocidade-Tempo
Se a linha no gráfico V-T tiver um declive positivo, o corpo
está sujeito a uma aceleração positiva.
 Se a velocidade é positiva o corpo está em movimento
uniformemente acelerado.
 Se a velocidade é negativa o corpo está em movimento
uniformemente retardado.

14. Gráficos Velocidade-Tempo
GRÁFICO V-T COM DECLIVE POSITIVO
t (s)
v(m/s)
N
S 𝑣 < 0; 𝑎 > 0
Movimento retardado
t (s)
v(m/s)
N
S𝑣 > 0; 𝑎 > 0
Movimento acelerado

15. Gráficos Velocidade-Tempo
Se a linha no gráfico V-T tiver um declive negativo, o corpo
está sujeito a uma aceleração negativa.
 Se a velocidade é positiva o corpo está em movimento
uniformemente retardado.
 Se a velocidade é negativa o corpo está em movimento
uniformemente acelerado.

16. Gráficos Velocidade-Tempo
GRÁFICO V-T COM DECLIVE NEGATIVO
t (s)
v(m/s)
N
S 𝑣 < 0; 𝑎 < 0
Movimento acelerado (no
sentido negativo)
t (s)
v(m/s)
N
S𝑣 > 0; 𝑎 < 0
Movimento retardado

17. Construção de gráficos
 Para construir um gráfico, utiliza-se um sistema de eixos cartesianos
ortogonais que são dois eixos perpendiculares entre si, sendo o ponto de
intersecção denominado origem.
 Os valores das grandezas envolvidas são colocados utilizando uma escala
adequada para cada eixo.
 O eixo na horizontal (por convenção) é denominado eixo das abcissas e
nele são colocadas os valores da variável independente (por exemplo,
tempo).
 O eixo na vertical é denominado eixo das ordenadas e nele são colocados
os valores da variável dependente (por exemplo, espaço).
17

18. Construção de gráficos
Para construir qualquer gráfico envolvendo grandezas físicas, deve-se
observar as seguintes regras:
 Coloque título e legenda.
 Escolha escalas adequadas para colocar os valores nos eixos.
 Coloque, de forma clara, as grandezas a serem representadas nos eixos com
as suas respetivas unidades.
 Coloque os valores das grandezas apenas com os números necessários à
leitura; não coloque valores especiais.
 Quando houver diversas séries de medidas, é conveniente distingui-las com
diferentes símbolos.
18

19. Relacionar grandezas 19
Fazendo a leitura de um gráfico podem retirar-se algumas
informações:
Vertical : Δs (variação da posição)
Horizontal: Δt (intervalo de tempo)
Declive (
𝚫𝒚
𝚫𝒙
):
Δ𝑠
Δ𝑡
= 𝑣 ou relacionando as unidades
𝑚
𝑠
(que é
a unidade de velocidade)
Área do gráfico: Δs x Δt ou m x s – neste exemplo não tem
significado físico!