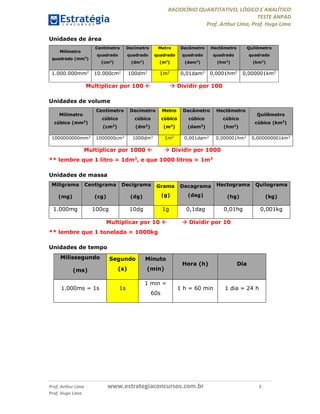
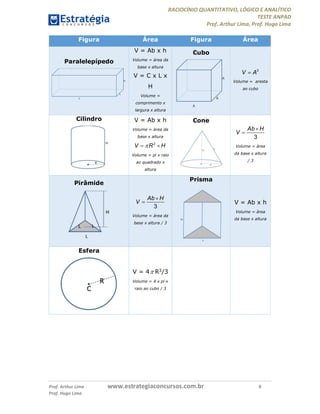
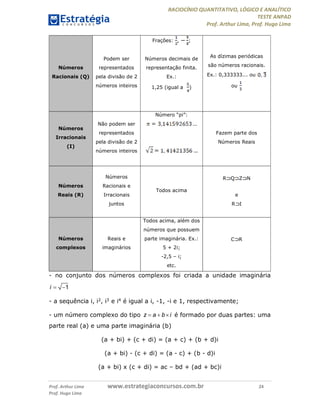
O documento resume os principais tópicos de raciocínio quantitativo, lógico e analítico para o teste ANPAD, incluindo fórmulas de combinações, arranjos e permutações, probabilidade, unidades de medida, porcentagem, progressões aritmética e geométrica, proporções, geometria e trigonometria.