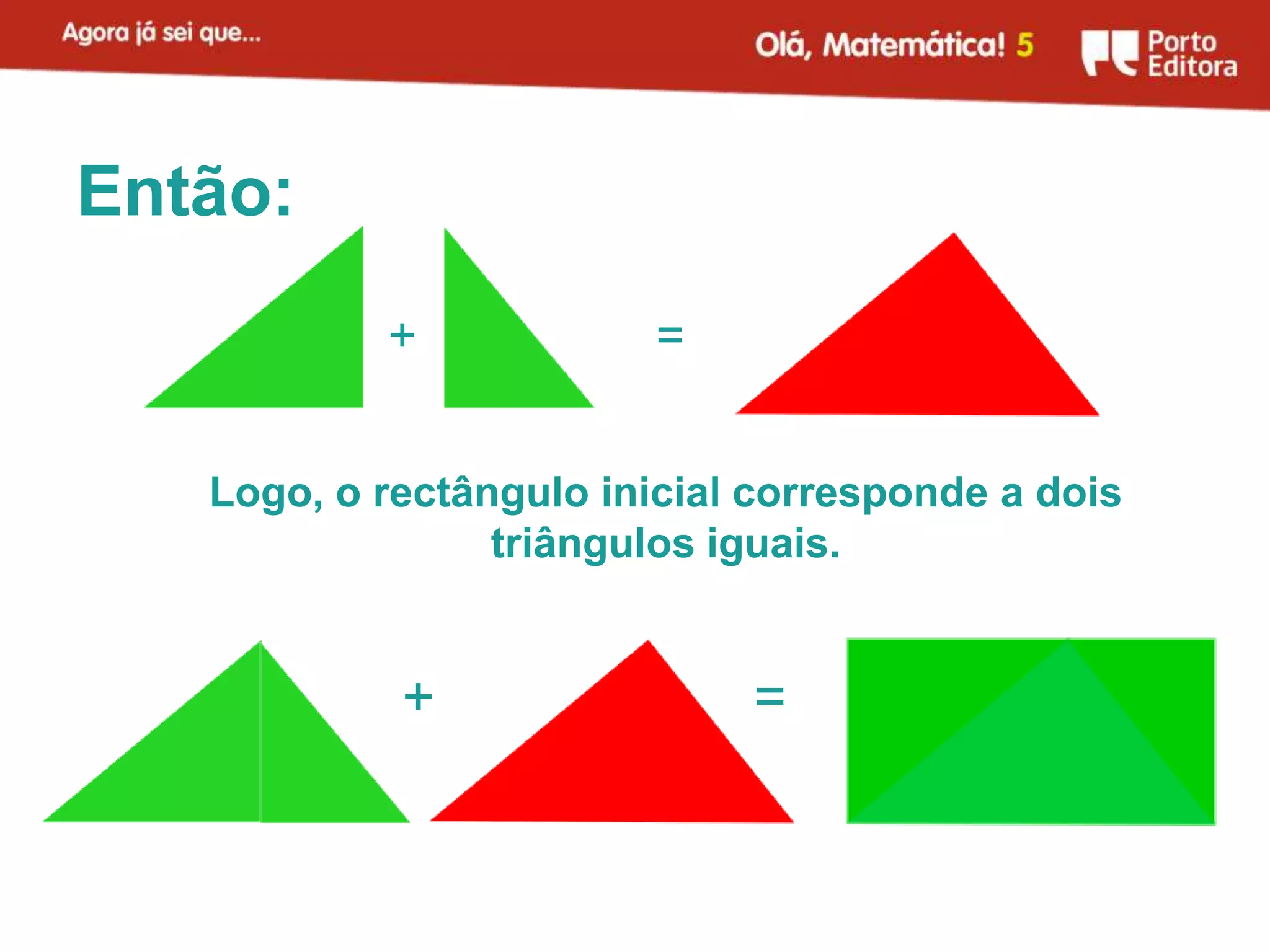
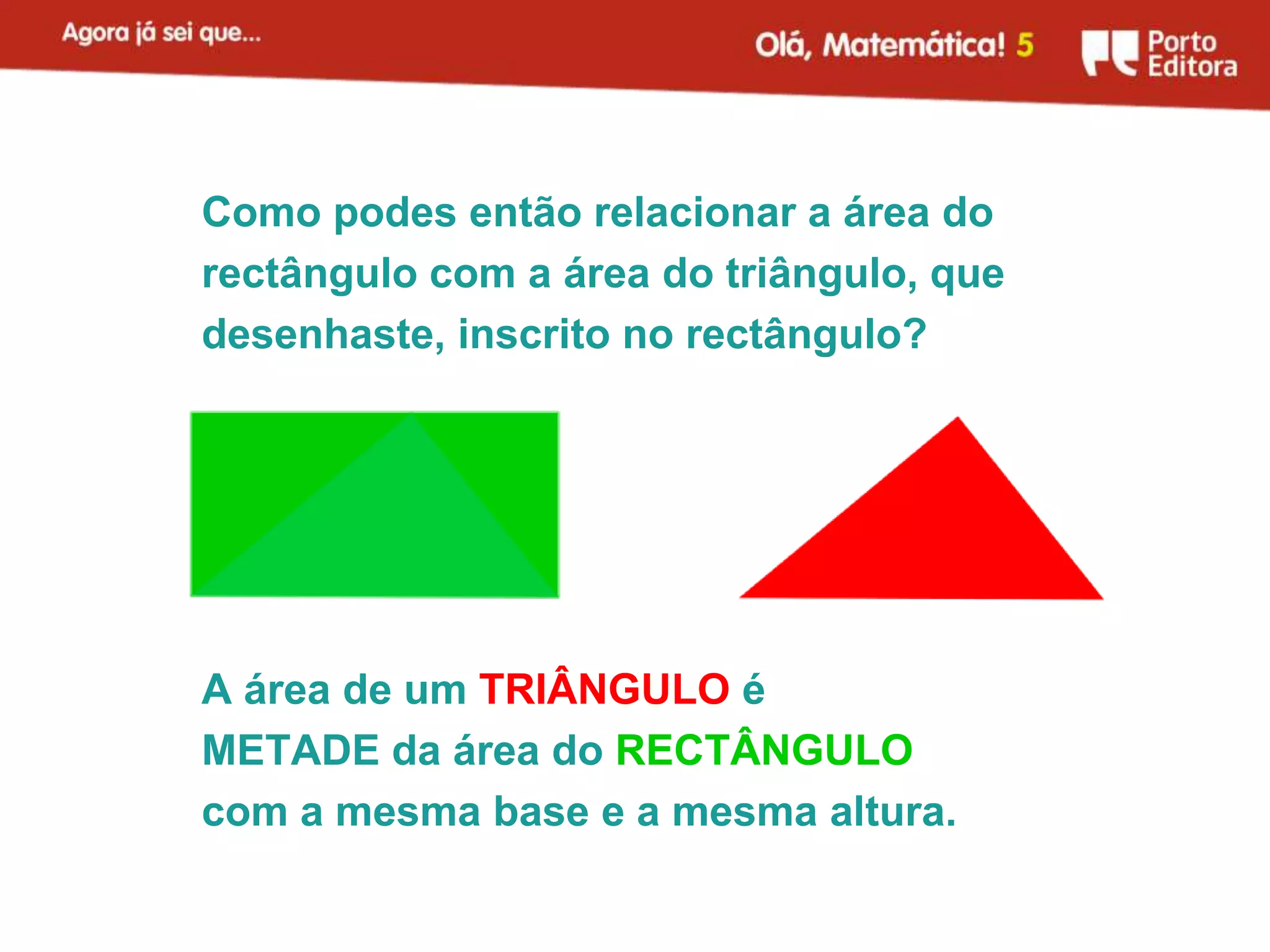
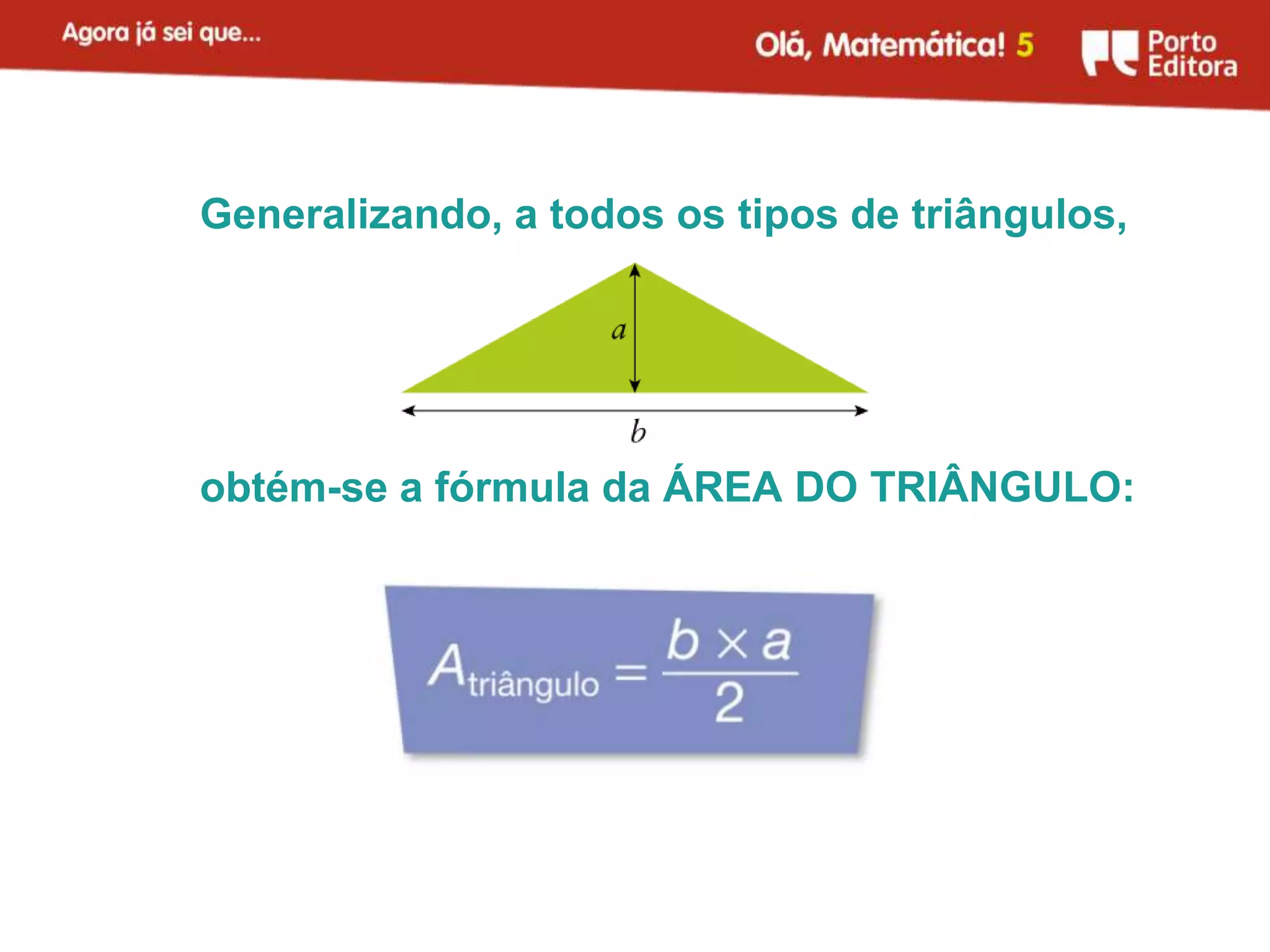
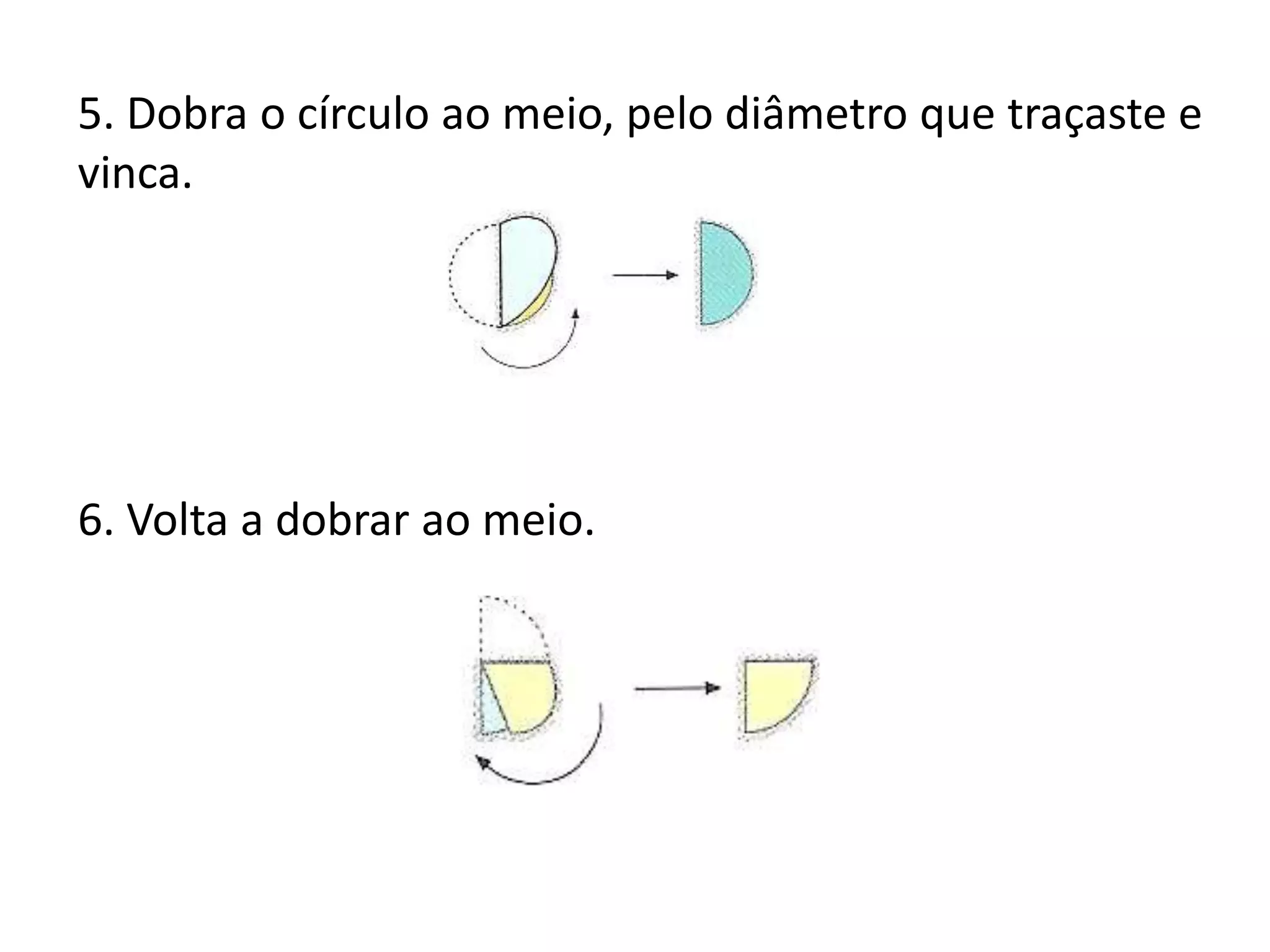
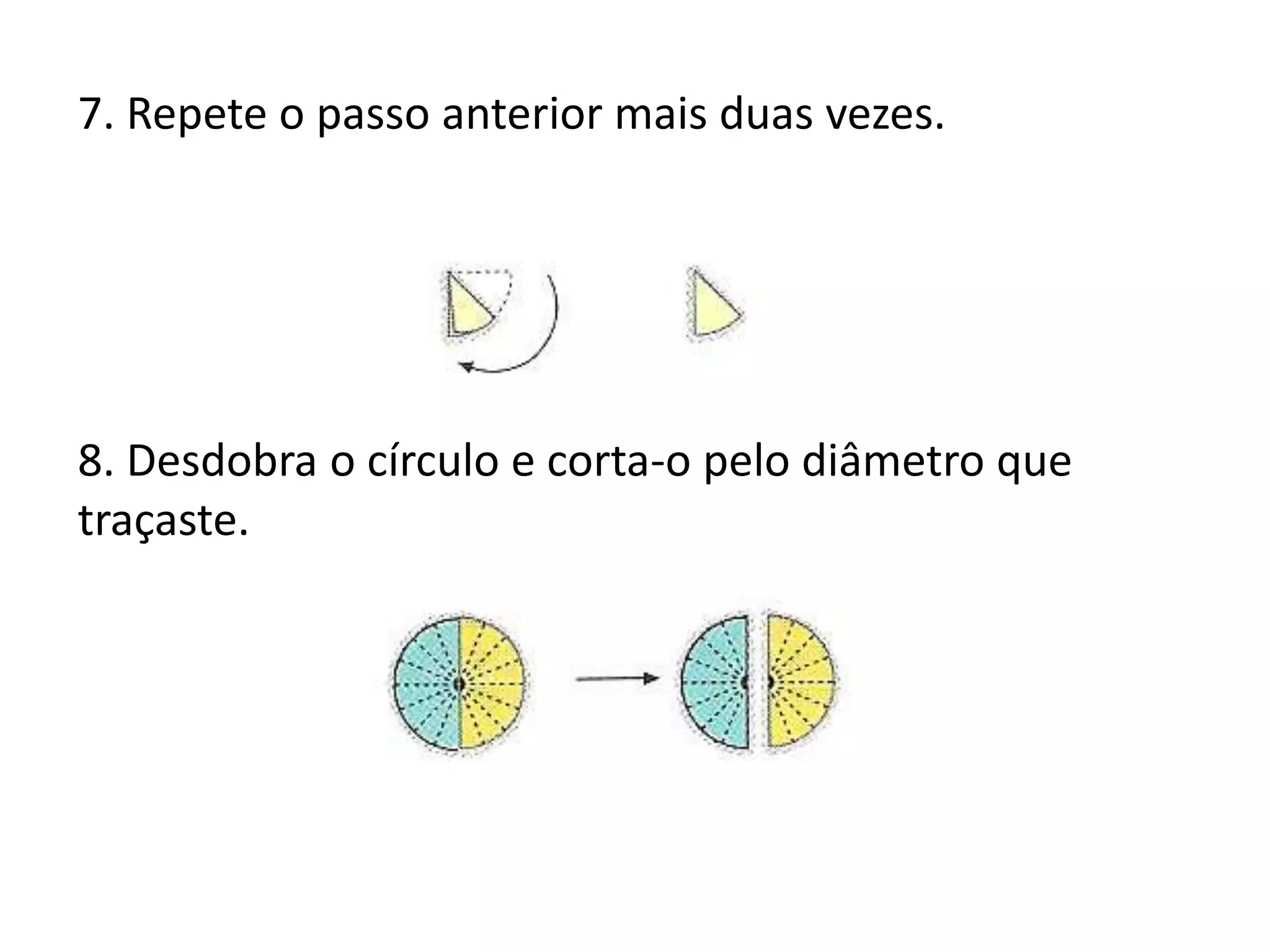
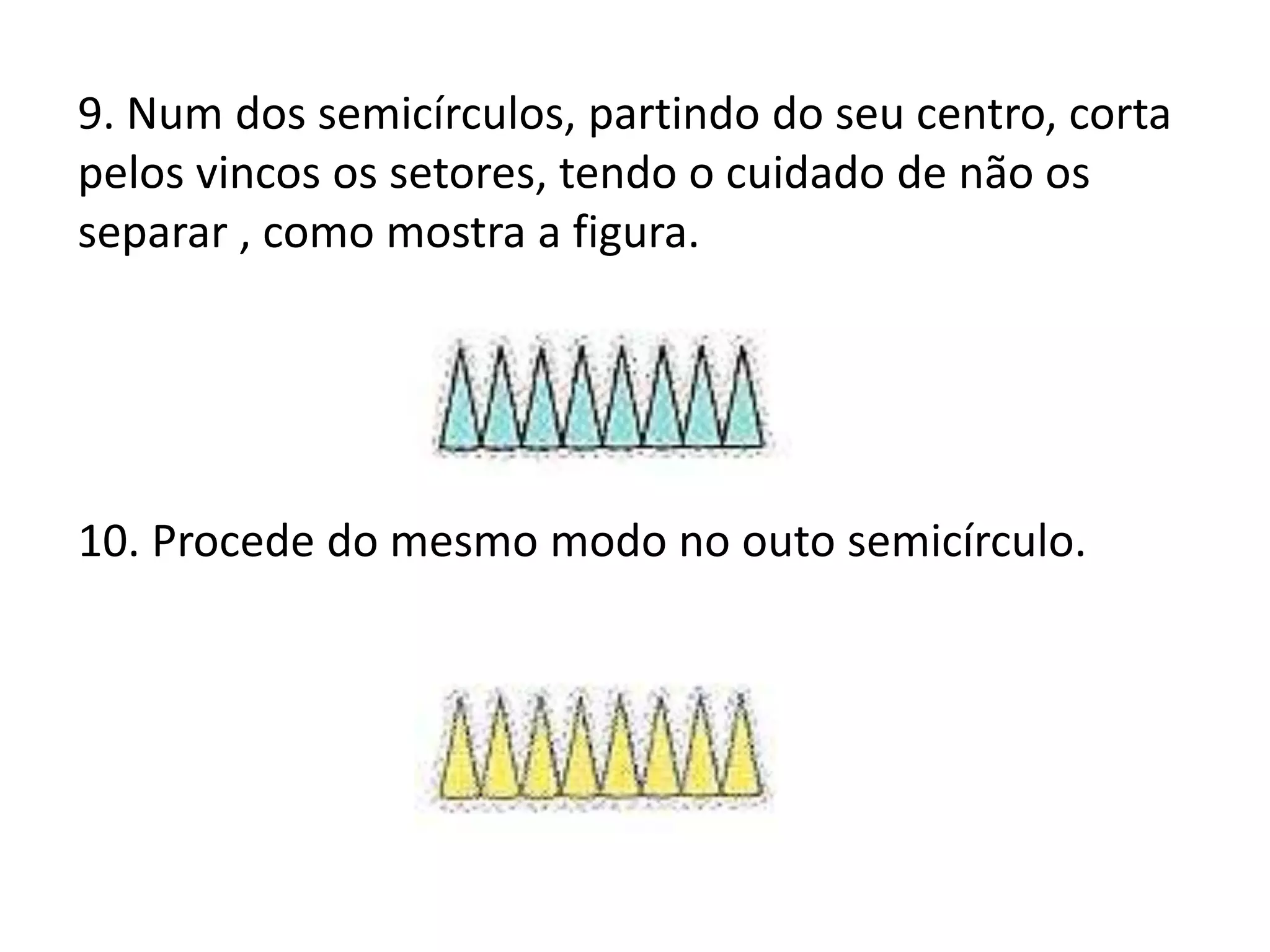
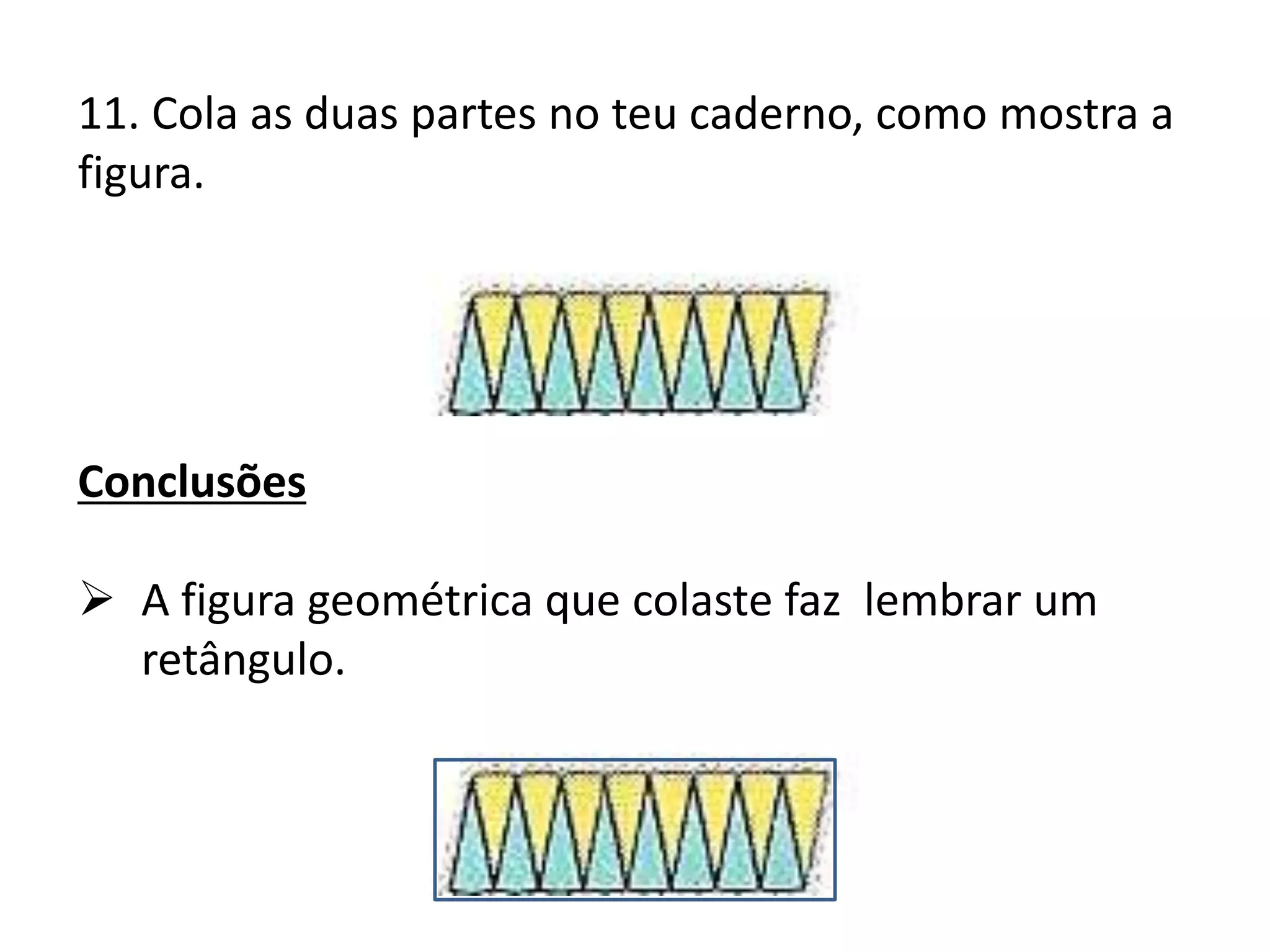
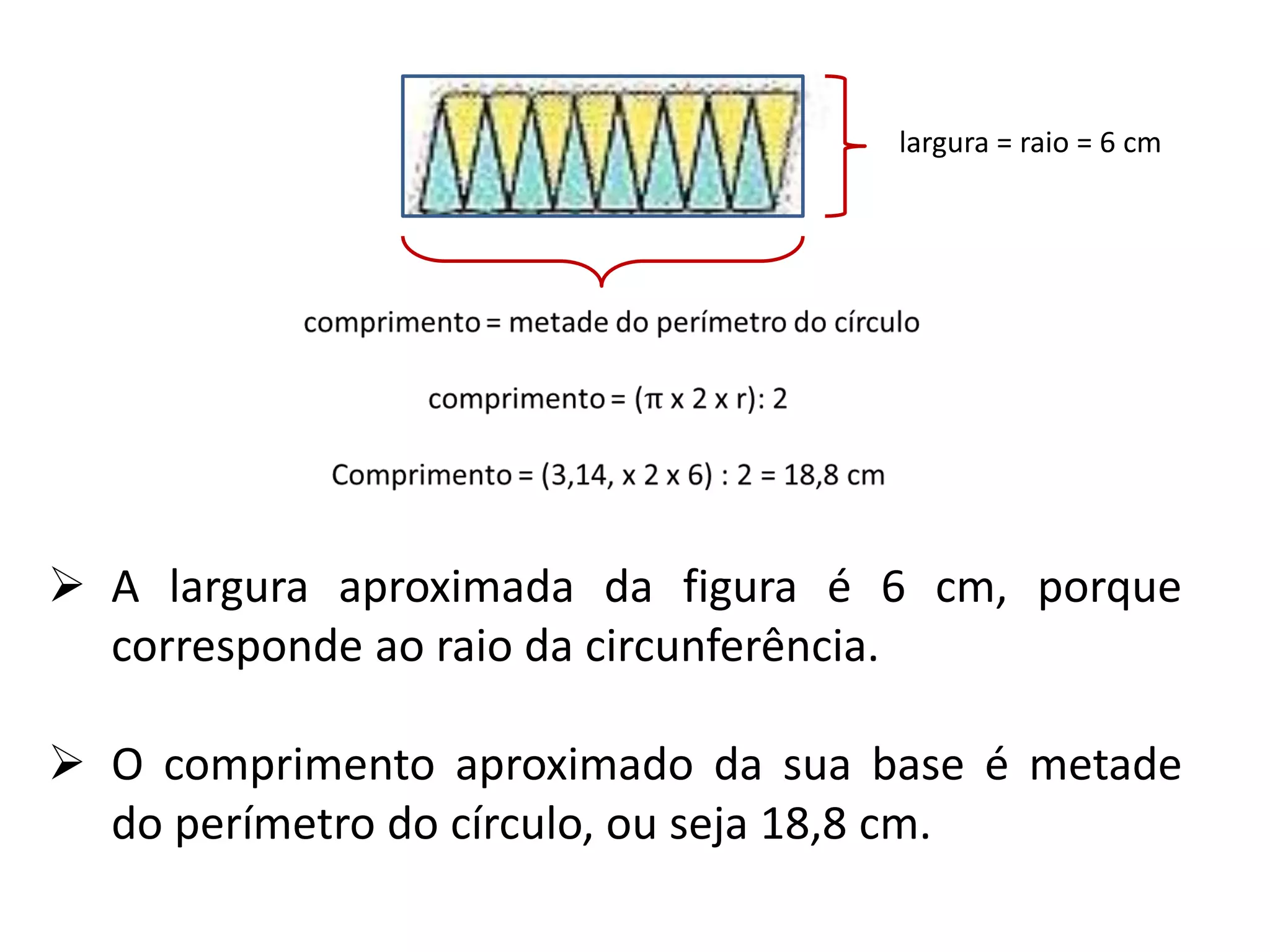
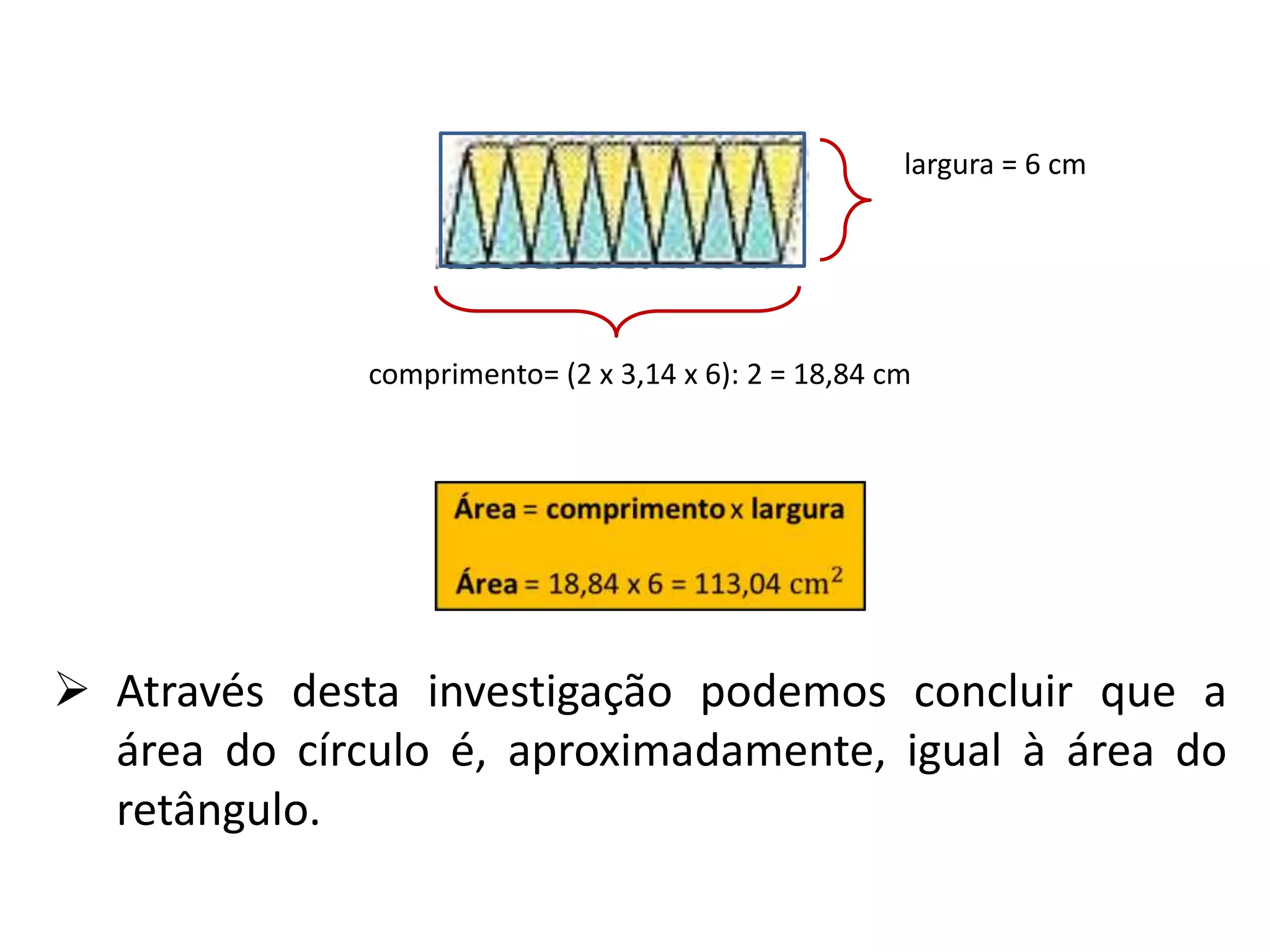
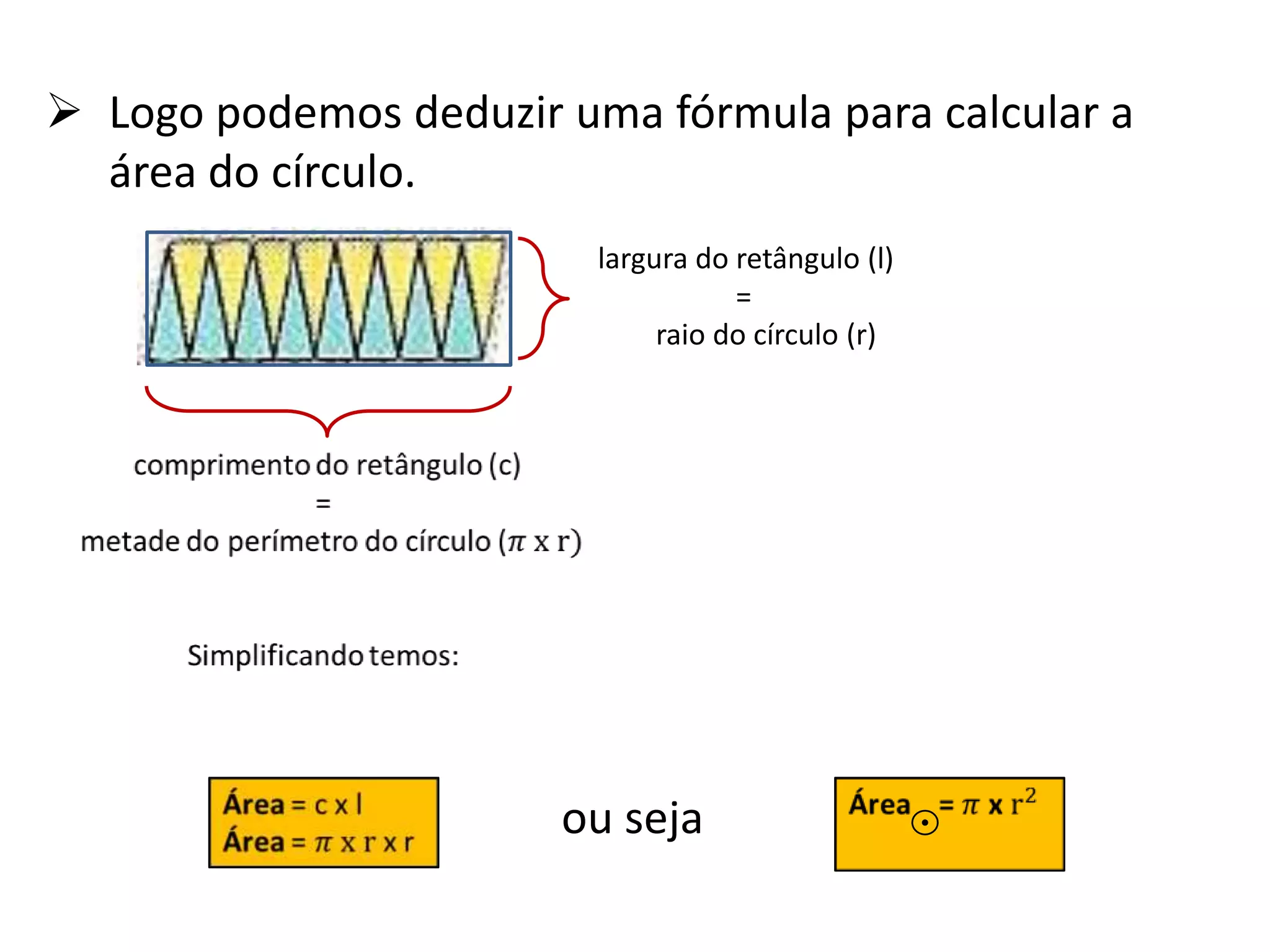
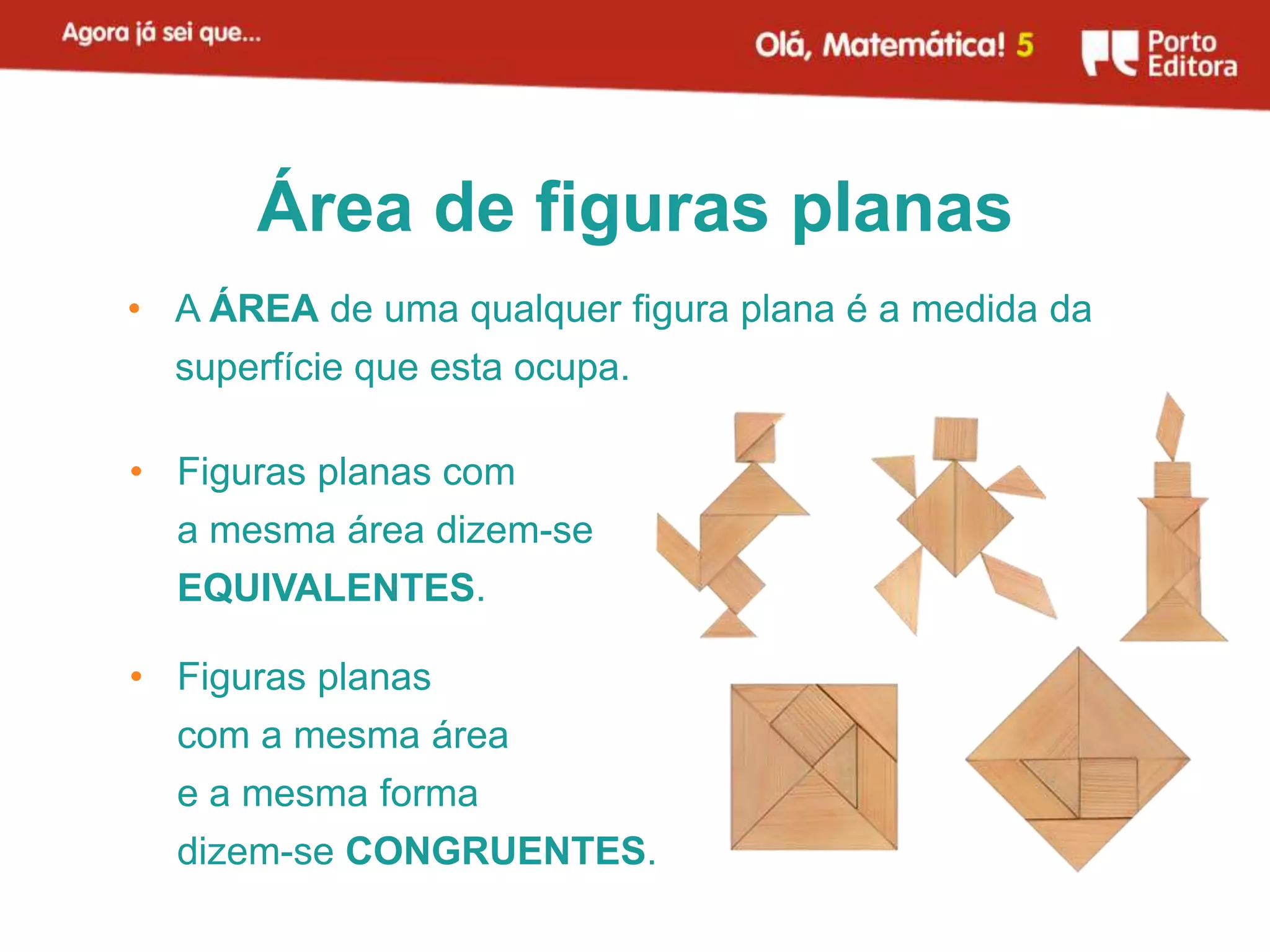
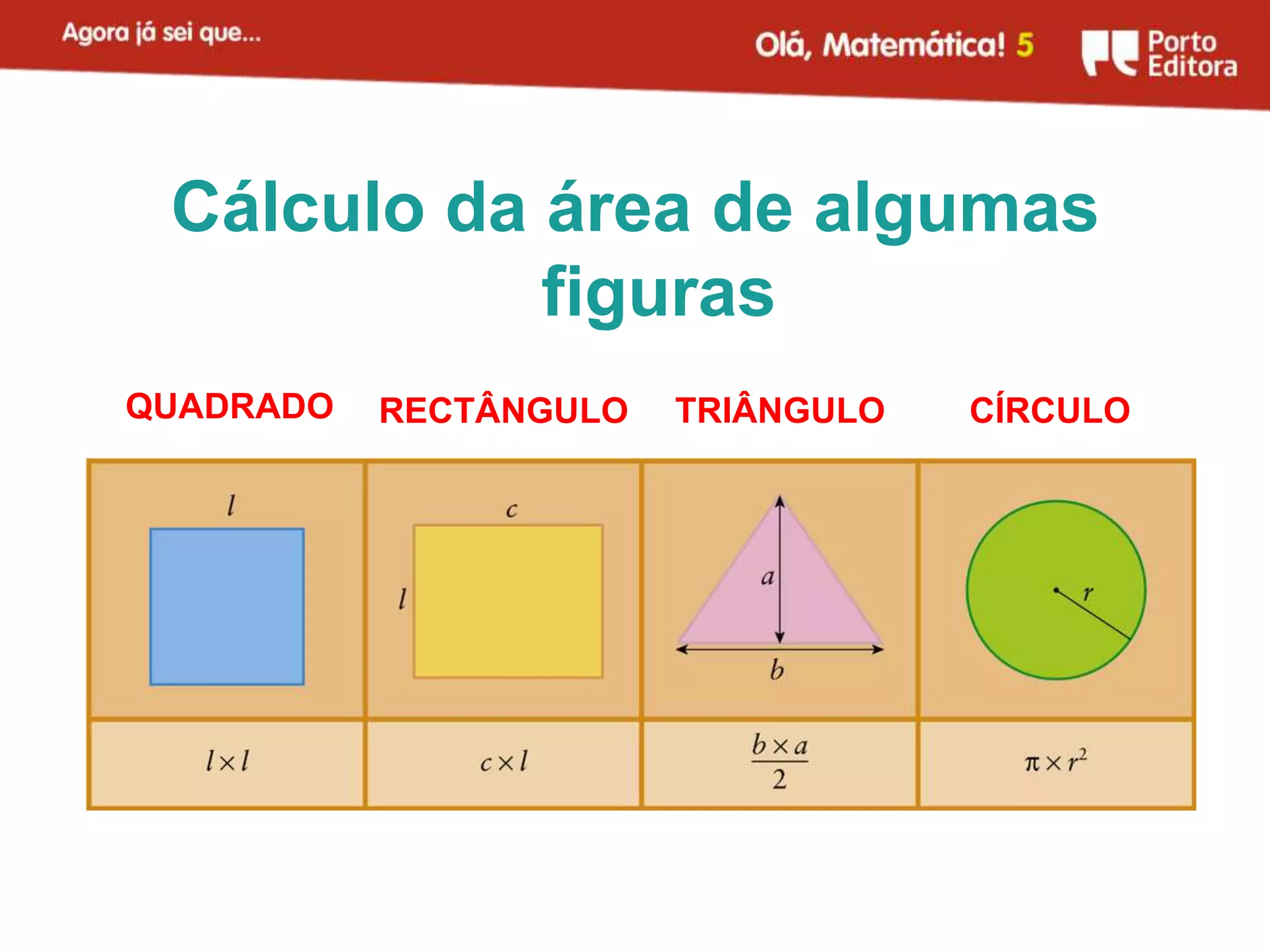
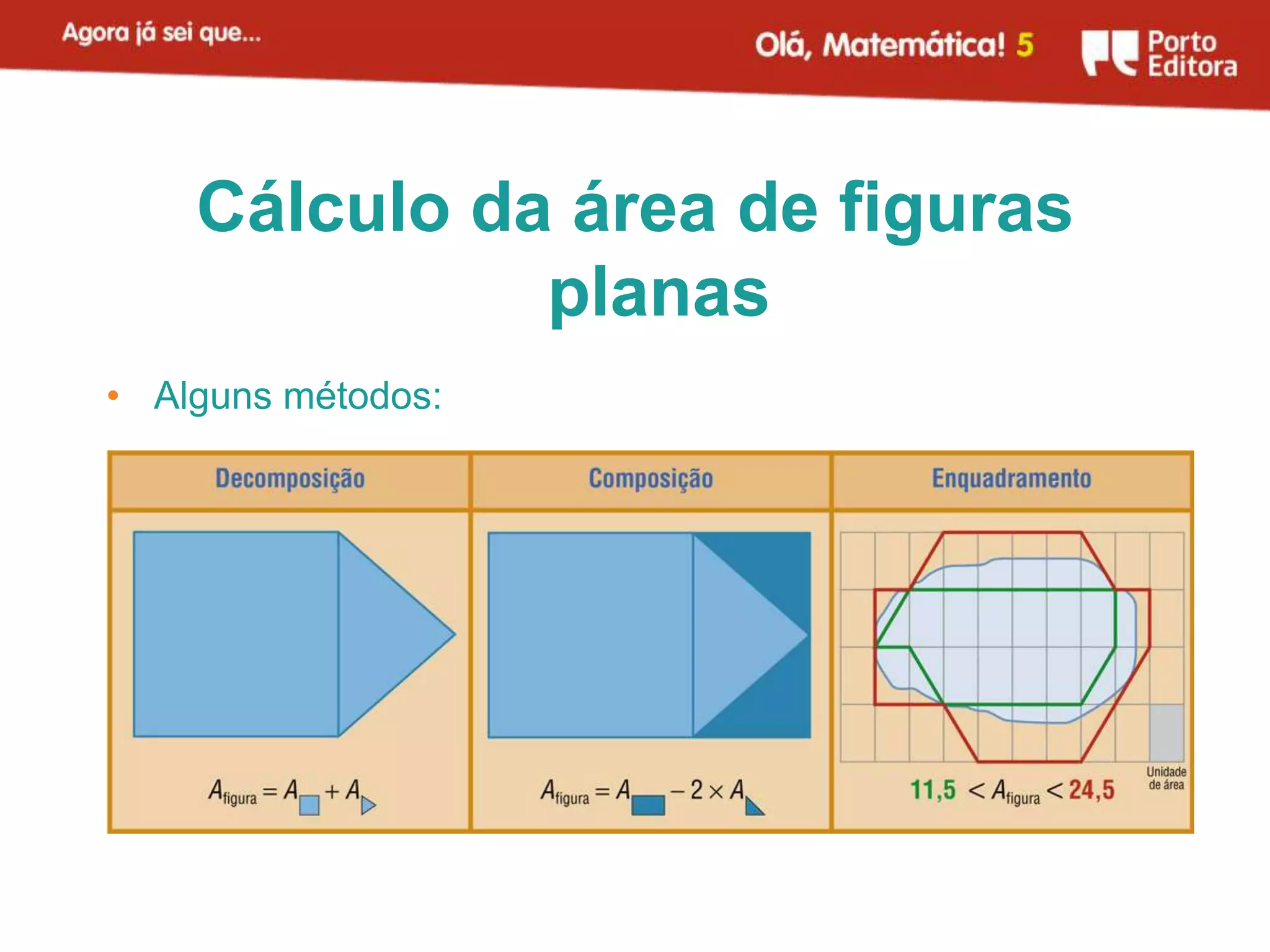
O documento apresenta métodos para calcular a área de triângulos e círculos. Explica-se que a área de um triângulo é metade da área de um retângulo com a mesma base e altura. Para o círculo, mostra-se que sua área é aproximadamente igual à de um retângulo com largura igual ao raio do círculo e comprimento igual à metade do perímetro. Apresenta-se também a fórmula para calcular a área do círculo.

2. Área do triângulo

3. Recorda:
• a forma de calcular
a área de um QUADRADO:
• a forma de calcular
a área de um RECTÂNGULO:

4. Qual será a relação entre a área de um TRIÂNGULO …
… e a área do RECTÂNGULO COM A MESMA BASE
E A MESMA ALTURA?

5. • Constrói um rectângulo em papel de cor verde e
um triângulo (inscrito no rectângulo), em papel
vermelho, com a mesma base e a mesma altura.

6. • Recorta o triângulo obtendo dois triângulos mais
pequenos em papel verde como se vê na figura:

7. • Sobrepõe os dois triângulos novos, ao triângulo
inicial e repara que, com os dois triângulos
novos, podes formar um triângulo igual ao inicial.

8. Então:
+ =
Logo, o rectângulo inicial corresponde a dois
triângulos iguais.
+ =

9. Como podes então relacionar a área do
rectângulo com a área do triângulo, que
desenhaste, inscrito no rectângulo?
A área de um TRIÂNGULO é
METADE da área do RECTÂNGULO
com a mesma base e a mesma altura.

10. Generalizando, a todos os tipos de triângulos,
obtém-se a fórmula da ÁREA DO TRIÂNGULO:

11. Área do círculo

12. 1. Desenha, numa folha branca, uma circunferência
com 6 cm de raio.
6 cm

13. 2. Traça um dos seus diâmetros.

14. 3. Contorna a preto uma das semicircunferências e a
azul-escura a outra.

15. 4. Pinta de azul claro um dos semicírculos e de amarelo
o outro.

16. 5. Dobra o círculo ao meio, pelo diâmetro que traçaste e
vinca.
6. Volta a dobrar ao meio.

17. 7. Repete o passo anterior mais duas vezes.
8. Desdobra o círculo e corta-o pelo diâmetro que
traçaste.

18. 9. Num dos semicírculos, partindo do seu centro, corta
pelos vincos os setores, tendo o cuidado de não os
separar , como mostra a figura.
10. Procede do mesmo modo no outo semicírculo.

19. 11. Cola as duas partes no teu caderno, como mostra a
figura.
Conclusões
 A figura geométrica que colaste faz lembrar um
retângulo.

20. largura = raio = 6 cm
 A largura aproximada da figura é 6 cm, porque
corresponde ao raio da circunferência.
 O comprimento aproximado da sua base é metade
do perímetro do círculo, ou seja 18,8 cm.

21. largura = 6 cm
comprimento= (2 x 3,14 x 6): 2 = 18,84 cm
 Através desta investigação podemos concluir que a
área do círculo é, aproximadamente, igual à área do
retângulo.

22.  Logo podemos deduzir uma fórmula para calcular a
área do círculo.
largura do retângulo (l)
=
raio do círculo (r)
ou seja

23. O que aprendi neste capítulo…
Agora já sei que...

24. Perímetro de figuras planas
• O PERÍMETRO de um polígono ou de uma qualquer
figura plana é o comprimento da linha que o delimita.
• Em particular, o perímetro do círculo é dado por:
P=×d ou P=2××r
(em que d e r representam, respectivamente,
o diâmetro e o raio do círculo e  = 3,141 592 65…)

25. Área de figuras planas
• A ÁREA de uma qualquer figura plana é a medida da
superfície que esta ocupa.
• Figuras planas com
a mesma área dizem-se
EQUIVALENTES.
• Figuras planas
com a mesma área
e a mesma forma
dizem-se CONGRUENTES.

26. Medidas de área
• Unidades do SISTEMA MÉTRICO:
• Correspondência entre unidades de MEDIDA DE ÁREA:
• MEDIDAS AGRÁRIAS:
1 a = 100 m2
1 ha = 10 000 m2

27. Cálculo da área de algumas
figuras
QUADRADO RECTÂNGULO TRIÂNGULO CÍRCULO

28. Cálculo da área de figuras
planas
• Alguns métodos: