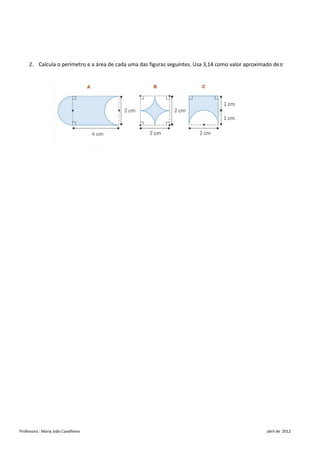
Este documento fornece informações sobre geometria e cálculo de áreas para alunos do 6o ano. Ele explica como calcular o perímetro de polígonos e círculos e como determinar se figuras planas são congruentes ou equivalentes. Além disso, fornece fórmulas e exemplos para calcular a área de triângulos, círculos, retângulos e outras figuras.

1. Escola Básica 2,3 de Ruy Belo
Ficha informativa de matemática 6º ano
Nome:______________________________________________ nº_____ data:__/___/____
Perímetro
• O perímetro de uma figura plana é o comprimento da linha que é sua fronteira.
• Calculamos o perímetro de um polígono somando todos os seus lados.
Exemplo:
Aplica:
1. Calcula o perímetro de cada terreno representado.
2. Utilizando os comprimentos indicados na figura calcula com comprimento desconhecido, sabendo que o
triângulo representado tem 19 m de perímetro.
Professora : Maria João Cavalheiro abril de 2012

2. 3. O Sr. Silva comprou um terreno como vês na figura.
3.1. De quantos metros de rede vai precisar?
3.2. Quanto pagou, em euros, pela rede, se cada metro custou 3€?
Perímetro do círculo
• Calcular o perímetro do círculo é determinar o comprimento da circunferência que o limita.
O perímetro do círculo é igual ao produto do diâmetro por
(pi, que tem um valor aproximado a 3,14).
• P=dx
• Sabendo que o diâmetro é o dobro do raio, também se pode calcular o perímetro do círculo a
partir do raio. Desta forma, o perímetro é igual ao produto do dobro do raio por .
• P=2xrx
Aplica
Professora : Maria João Cavalheiro abril de 2012

3. 1. Completa os quadros seguintes. Utiliza 3,14 como valor aproximado de
Diâmetro Perímetro do círculo Raio Perímetro do círculo
9 cm 7 cm
25 mm 4,5 dm
2. Calcula o comprimento das linhas escuras em cada uma das figuras.
Equivalência de figuras planas
• Duas figuras são congruentes se sobrepuserem ponto por ponto.
• Os triângulos da figura são congruentes.
• Com estes quatro triângulos construíram-se outros polígonos.
Observa:
Estas três figuras planas não são congruentes, não têm a mesma forma, mas foram construídas com as mesmas
quatros peças.
Dizemos que são figuras planas equivalentes. De duas figuras planas equivalentes, dizemos têm a mesma área.
Em resumo:
• Figuras planas congruentes são sempre equivalentes.
• Figuras planas equivalentes têm sempre a mesma área, mas podem ser, ou não, congruentes.
Professora : Maria João Cavalheiro abril de 2012

4. Aplica:
1. Observa as figuras.
1.1. Identifica duas figuras congruentes. Justifica a tua resposta.
________________________________________________________________________________________
1.2. Indica duas figuras equivalentes, mas não congruentes.
_________________________________________________________________________________________
1.3. Desenha um retângulo equivalente à figura E.
Unidades de área
Professora : Maria João Cavalheiro abril de 2012

5. Aplica:
1.
2. Completa
225 dm2= ________cm2 0,006 hm2= ________m2
Área do triângulo
Professora : Maria João Cavalheiro abril de 2012

6. Em resumo:
Aplica:
1. Calcula a área, em centímetros quadrados, de cada uma dos triângulos seguintes.
Professora : Maria João Cavalheiro abril de 2012

7. Área do círculo
Em resumo:
Aplica:
1. Calcula a área de um círculo com 14 cm de diâmetro. Utiliza 3,14 como valor aproximado de
Professora : Maria João Cavalheiro abril de 2012

8. 2. Calcula o perímetro e a área de cada uma das figuras seguintes. Usa 3,14 como valor aproximado de
Professora : Maria João Cavalheiro abril de 2012