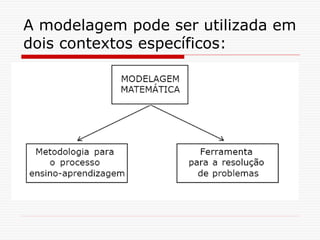
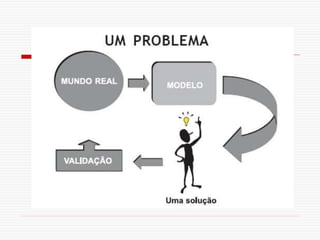
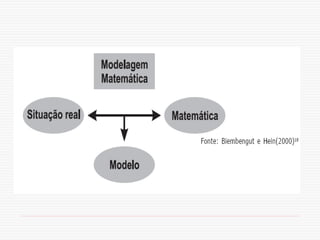
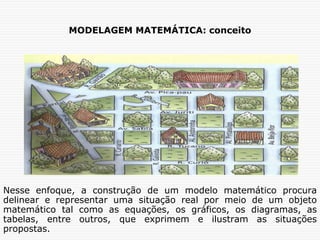
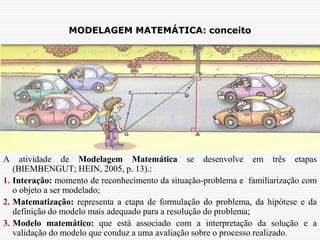
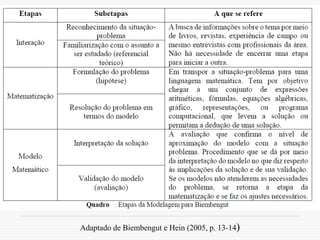
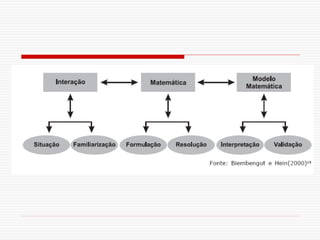
O documento discute a modelagem matemática como uma alternativa de ensino e aprendizagem em matemática. A modelagem matemática envolve transformar problemas do mundo real em problemas matemáticos e interpretar suas soluções na linguagem do mundo real. Ela ocorre em três etapas: interação, matematização e modelo matemático. A modelagem pode ser usada para promover a articulação entre conhecimento matemático e a realidade, exigindo diálogo interdisciplinar.

2. A MODELAGEM MATEMÁTICA COMO
ALTERNATIVA DE ENSINO E
APRENDIZAGEM EM MATEMÁTICA

3. MODELAGEM MATEMÁTICA: conceito
Cada dia mais e mais, as pessoas tentam mostrar o
conhecimento matemático voltado ao dia a dia das pessoas,
procurando sempre e sempre novas metodologias de Ensino
que possam proporcionar Aprendizagem ....

4. MODELAGEM MATEMÁTICA: conceito
“[...] a Modelagem Matemática consiste na arte de
transformar problemas da realidade em problemas
matemáticos e resolvê-los interpretando suas soluções na
linguagem do mundo real.”
Bassanezi (2002, p.16),

5. MODELAGEM MATEMÁTICA: conceito
Nesse enfoque, a construção de um modelo matemático procura
delinear e representar uma situação real por meio de um objeto
matemático tal como as equações, os gráficos, os diagramas, as
tabelas, entre outros, que exprimem e ilustram as situações
propostas.

6. MODELAGEM MATEMÁTICA: conceito
A atividade de Modelagem Matemática se desenvolve em três etapas
(BIEMBENGUT; HEIN, 2005, p. 13).:
1. Interação: momento de reconhecimento da situação-problema e familiarização com
o objeto a ser modelado;
2. Matematização: representa a etapa de formulação do problema, da hipótese e da
definição do modelo mais adequado para a resolução do problema;
3. Modelo matemático: que está associado com a interpretação da solução e a
validação do modelo que conduz a uma avaliação sobre o processo realizado.

7. Interação
Num primeiro momento é importante que se
reconheça a situação-problema, bem como se
levante o referencial teórico relativo ao assunto
que será modelado. Esta etapa não termina com o
início da próxima, visto que a situação-problema
torna-se mais clara à medida que se interage com
os dados.

8. Matematização
É uma etapa desafiante e complexa pois é nela que se
expressa o problema em linguagem matemática. Nesta etapa
identificamos os fatos envolvidos, classificando as
informações como relevantes ou não. Levantamos as
hipóteses, selecionamos variáveis e constantes envolvidas e
descrevemos as relações em termos matemáticos. Após a
formulação do problema, passamos à resolução ou à análise
com as ferramentas matemáticas disponíveis.
Esta etapa exige um conhecimento considerável dos objetos
matemáticos e muitas vezes o uso do computador pode-se
tornar imprescindível.

9. Modelo Matemático
Para concluir e validar o modelo é necessário
avaliar e definir o quanto ele se aproxima da
situação-problema representada, bem como o
grau de confiabilidade de sua utilização.

10. Adaptado de Biembengut e Hein (2005, p. 13-14)

12. MODELAGEM MATEMÁTICA: conceito
O essencial, na Modelagem empregada na educação, é
o processo realizado pelo aluno para chegar à solução
de um problema, além da análise crítica dos resultados
alcançados. Dessa forma, ele se prepara para
participar, como elemento ativo, na sociedade em que
vive.

13. Modelagem Matemática como alternativa metodológica
Argumentos:
Argumento formativo
Argumento de competência crítica
Argumento de utilidade
Argumento intrínseco
Argumento de aprendizagem
Argumento de alternativa epistemológica
Bassanezi (2002, p.36)

14. Modelagem Matemática como alternativa metodológica
Obstáculos:
Obstáculo institucional
Obstáculo para o aluno
Obstáculo para o professor
Bassanezi (2002)

15. Modelagem Matemática como
alternativa metodológica
Para BIEMBENGUT; HEIN, 2005 :
Os argumentos que alicerçam o uso da Modelagem como metodologia de ensino
e de aprendizagem em Matemática, propõe alternativas com o intuito de superar
obstáculos, promovendo a articulação entre o conhecimento matemática e a
realidade vivida , exigindo também dialogo constante entre áreas do saber
de forma interdisciplinar tendo em vista um novo olhar diante do estudo de
matemática.
“[...] a adoção da Modelagem demanda maiores
qualificações do professor, como por exemplo,
disposição para adquirir conhecimentos
interdisciplinares. Mas ele necessita, sobretudo, do
espírito inovador, aumentando sua iniciativa para a
pesquisa e de flexibilidade perante os obstáculos”.
Barbosa (1999, p.79)

16. A modelagem pode ser utilizada em
dois contextos específicos:

17. O que é um modelo matemático?
 De forma geral, podemos dizer que um
modelo é uma representação simplificada
de algum fenômeno ou situação real.
 O modelo matemático é uma representação
simplificada, porém tendo como
característica o uso de um conjunto de
símbolos e relações matemáticas. Desta
forma, representa o objeto ou fenômeno
estudado, ou ainda, o problema
proveniente de uma situação real.

18. Um modelo matemático pode ser formulado a
partir de expressões numéricas ou fórmulas,
diagramas ou tabelas, expressões algébricas ou
ainda representações gráficas. Os programas
computacionais podem ajudar muito na
apresentação e obtenção de um modelo. É
importante, porém, que tenha uma linguagem
concisa e que expresse as idéias de maneira clara
e sem ambigüidades.

19. Veja alguns modelos de
aeronaves.
 Observe que, a partir de cada modelo
podemos delinear somente algumas
características do objeto real.
 Perceba que estes não são modelos
matemáticos.

20.  Agora veja um modelo matemático.
 Trata-se de um modelo para a
dinâmica populacional de uma nova
colméia de abelhas. É descrito da
seguinte forma: o crescimento
populacional de uma colméia é
proporcional à diferença entre a
população máxima sustentável e a
população dada em cada instante.

22. No contexto da modelagem
matemática, um modelo fica inserido
num processo de decisão, na solução
de um problema real, permitindo
relacionar os diversos elementos de
forma mais simples que o real.

24. Etapas da modelagem matemática
 Na construção de um modelo são
necessárias criatividade e intuição,
além do conhecimento de
Matemática, visto que é importante
interpretar o contexto, identificar as
variáveis e o conteúdo matemático
que melhor se adapte a determinada
situação.

26. Atividade: “Tamanho do pé”.
Biembengut e Hein (2005):
Etapas da Modelagem Matemática e o Ensino da Matemática
1ª etapa: Interação com o assunto
a) reconhecimento da situação problema e
b) familiarização com o assunto a ser modelo-pesquisa
Fonte da Atividade: Dente; Rehfeldt; Quartieri, 2016

39. Referências