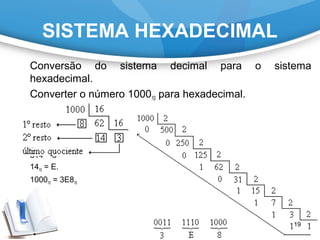
O documento discute os sistemas de numeração binário, octal, hexadecimal e suas conversões. Explica que o sistema binário usa apenas 0 e 1, e como representar números maiores. Também mostra como converter entre esses sistemas numéricos e o sistema decimal.

1. Sistema deSistema de
NumeraçãoNumeração
Aula 3Aula 3
1

2. INTRODUÇÃO
2

3. SISTEMA BINÁRIO
O sistema binário de numeração é um sistema no
qual existem apenas dois algarismos:
Algarismo “0” (zero) e
Algarismo “1” (um).
3

4. SISTEMA BINÁRIO
Para representarmos a quantidade zero,
utilizamos o algarismo (0), para representarmos a
quantidade um utilizamos o algarismo (1).
E para representarmos a quantidade dois, se nós
não possuímos o algarismo (2) nesse sistema?
4

5. SISTEMA BINÁRIO
Conversão do sistema binário para o sistema
decimal.
5

6. SISTEMA BINÁRIO
Conversão do sistema decimal para o sistema
binário.
1011112 = 4710
6

7. SISTEMA BINÁRIO
Números binários e decimais fracionários e suas
conversões.
Até agora tratamos de números inteiros. Mas, se
tivéssemos de converter o número 101,1012 para a
base dez, qual seria o nosso procedimento?
7

8. SISTEMA BINÁRIO
1 x 22
+ 0 x 21
+ 1 x 20
+ 1 x 2-1
+0 x 2-2
+ 1 x 2-3
=
1 x 4 + 0 x 2 + 1 x 1 + 1 x +0 x + 1 x =
4 + 0 + 1 + 0,5 + 0 + 0,125 =
5 + 0,5 + 0,125 = 5,62510
Portanto: 101,1012 = 5,62510
8

9. SISTEMA BINÁRIO
Conversão de um número decimal fracionário em
binário.
Por exemplo, para transformarmos o número
8,375 em binário.
Temos, então: 810 = 10002
9

10. SISTEMA BINÁRIO
Isso feito, o passo a seguir é transformar a parte
fracionária, para tal utilizamos a seguinte
sequência:
10

11. SISTEMA BINÁRIO
Logo o número 8,37510, em binário ficará:
11

12. SISTEMA OCTAL
O sistema octal de numeração é um sistema no
qual existem oito algarismos que são:
0, 1, 2, 3, 4, 5, 6 e 7.
12

13. SISTEMA OCTAL
Para convertermos um número octal em decimal,
utilizamos os conceitos básicos de formação de um
número.
Vamos, por exemplo, converter o número 1448 em decimal:
13

14. SISTEMA OCTAL
Conversão do sistema octal para o sistema binário
o número octal 278. Desmembremos esse número
em dois algarismos e transformemos cada
algarismo no seu correspondente binário.
Portanto: 278 = 101112
14

15. SISTEMA OCTAL
Conversão do sistema binário para o sistema octal
o número 1100102. Para transformarmos esse
número em octal, dividimos em grupos de três
algarismos a partir da direita: 110 010
Podemos notar que o maior número que se pode
formar com três algarismos binários é o número 7.
Então: 1100102 = 628
15

16. SISTEMA HEXADECIMAL
Conversão do sistema hexadecimal para o
sistema decimal.
Tomemos, por exemplo, o número hexadecimal
3F16 e vamos convertê-lo em decimal:
16

17. SISTEMA HEXADECIMAL
Conversão do sistema hexadecimal para o
sistema binário.
Vamos, então, converter o número C1316 para o
sistema binário.
Portanto: C1316 = 1100000100112
17

18. SISTEMA HEXADECIMAL
Conversão do sistema binário para o sistema
hexadecimal.
Converter o número 100110002 para hexadecimal
Então: 100110002 = 9816
18

19. SISTEMA HEXADECIMAL
Conversão do sistema decimal para o sistema
hexadecimal.
Converter o número 100010 para hexadecimal.
314 8
1410 = E.
100010 = 3E816
19

20. MATEMÁTICA
FIM DA
AULA 3
20