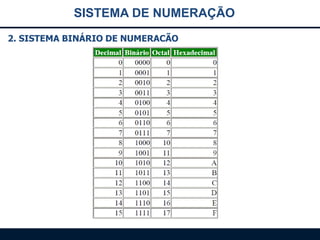
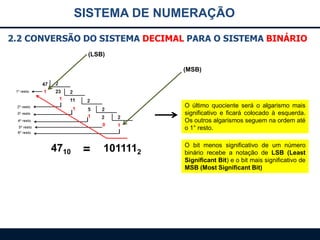
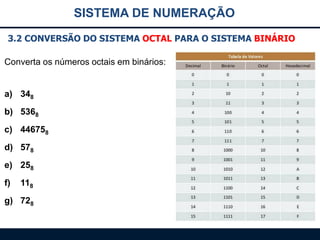
Este documento apresenta os principais sistemas de numeração, incluindo o sistema decimal, binário, octal e hexadecimal. O conteúdo inclui: 1) introdução aos sistemas de numeração; 2) detalhes sobre o sistema binário, incluindo conversões entre binário e decimal; 3) detalhes sobre o sistema octal, incluindo conversões.

1. Professor:
Marcelo Vianello (MsC.)
AULA 2
Organização e Arquitetura de
Computadores

2. Objetivo da Aula
Apresentar os conceitos dos Sistema de Numeração,
destacando o sistema decimal, binário, octal e
hexadecimal

3. Conteúdo Geral da Aula
1. Introdução
2. O Sistema Binário de Numeração
3. O Sistema Octal de Numeração
4. O Sistema Hexadecimal de Numeração

4. 1. Introdução

5. SISTEMA DE NUMERAÇÃO
1. INTRODUÇÃO
O homem, através dos tempos, sentiu a necessidade da utilização de
sistemas numéricos.
Existem vários sistemas numéricos, dentre os quais se destacam:
 O sistema decimal;
 O sistema binário;
 O sistema octal;
 E o sistema hexadecimal.

6. SISTEMA DE NUMERAÇÃO
1. INTRODUÇÃO
O sistema decimal é utilizado por nós no dia-a-dia e é, sem dúvida, o mais
importante dos sistemas numéricos. Trata-se de um sistema que possui 10
(dez) algarismos, com os quais podemos formar qualquer número através da
lei da formação.
Os outros sistemas (binário, octal e hexadecimal) são importantes nas áreas
de técnicas digitais e informática.

7. 2. O Sistema Binário de Numeração

8. SISTEMA DE NUMERAÇÃO
2. SISTEMA BINÁRIO DE NUMERACÃO
No sistema binário de numeração, existem apenas dois (02) algarismos. São
eles:
 O algarismos “0” (zero) e
 O algarismo “1” (um)

9. SISTEMA DE NUMERAÇÃO
2. SISTEMA BINÁRIO DE NUMERACÃO
Informação Importante. Se não possuímos o algarismo 2 nesse sistema,
como devemos representá-lo?
No sistema decimal, não possuímos o algarismo “dez”, e representamos a
quantidade de uma dezena utilizando o algarismo “1”, seguido do algarismo
“0”. Neste caso, significará que temos um grupo de uma dezena e o
algarismo “0” nenhuma unidade, o que significa “dez”.
No sistema binário é a mesma coisa. Agimos da mesma forma. Para
representarmos a quantidade “dois”, utilizamos o algarismo “1” seguido do
algarismo “0”. O algarismo 1 significará que temos um grupo de “dois”
elementos e o “0” o grupo de nenhuma unidade, representando assim o
número “dois”.

10. SISTEMA DE NUMERAÇÃO
2. SISTEMA BINÁRIO DE NUMERACÃO

11. SISTEMA DE NUMERAÇÃO
2. SISTEMA BINÁRIO DE NUMERACÃO
Cada dígito binário recebe a denominação de bit (binary digit). O conjunto de
4 bits é denominado de nibble e um conjunto de 8 bits corresponde a um
byte ou octeto (Binary Term – muito utilizado para especificar o tamanho ou
a quantidade de memória e a capacidade de armazenamento de um
determinado dispositivo). Termo bastante utilizado na área de informática.

12. SISTEMA DE NUMERAÇÃO
2.1 CONVERSÃO DO SISTEMA BINÁRIO PARA O SISTEMA DECIMAL
Para explicar a conversão, vamos utilizar como exemplo, o número decimal
594.
Este número significa o seguinte:
(5 x 100) + (9 x 10) + (4 x 1) = 594
Esquematicamente, temos:
dezena
101)
100)
1
9
4
unidade
102)
10
5
centena
100
(5 x
+ (9 x
+ (4 x
= 594
102
5
101 100
9
4
Utilizando o conceito básico de formação de um número, podemos obter a
mesma equivalência, convertendo assim o número binário para o sistema
decimal.

13. SISTEMA DE NUMERAÇÃO
2.1 CONVERSÃO DO SISTEMA BINÁRIO PARA O SISTEMA DECIMAL
Para explicar a conversão do sistema binário para o sistema decimal,
vamos utilizar como exemplo, o número binário 1012.
22
21
20
1
0
1
=
(1 x 22) + (0 x 21) + (1 x 20) = 5
Portanto, o número 101 na base 2 é igual ao número 5 na base 10.
Para melhor identificação do número, colocaremos como índice, a
base do sistema ao qual o número pertence. Para o nosso exemplo,
podemos escrever: 510 = 1012

14. SISTEMA DE NUMERAÇÃO
2.1 CONVERSÃO DO SISTEMA BINÁRIO PARA O SISTEMA DECIMAL
Exemplo:
22
21
20
1
0
1
=
(1 x 22) + (0 x 21) + (1 x 20) = 5
Seguindo o exemplo acima, façam a conversão do sistema binário para o
sistema decimal:
a)
10012
b)
011102
c)
10102
d)
11001100012
e)
10112
f)
111112

15. SISTEMA DE NUMERAÇÃO
2.1 CONVERSÃO DO SISTEMA BINÁRIO PARA O SISTEMA DECIMAL
a)
10012
(1 x 23) + (0 x 22) + (0 x 21) (1 x 20) = 910
b)
011102
(1 x 23) + (1 x 22) + (1 x 21) (0 x 20) = 1410
c)
10102
(1 x 23) + (0 x 22) + (1 x 21) + (0 x 20) = 1010
d)
11001100012
(1 x 29) + (1 x 28) + (1 x 25) + (1 x 24) + (1 x 20) = 512+256+32+16+1 = 81710
e)
10112
(1 x 23) + (0 x 22) + (1 x 21) + (1 x 20) = 1110
f)
111112
(1 x 24) + (1 x 23) + (1 x 22) + (1 x 21) + (1 x 20) = 3110

16. SISTEMA DE NUMERAÇÃO
2.2 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA BINÁRIO
Veremos agora a conversão do Sistema Decimal para o Sistema Binário.
Para este tipo de conversão, basta você dividir o número decimal por 2,
conforme demonstrado no exemplo a seguir, com o número decimal 47.
47
1º resto
2
1
23
1
2º resto
3º resto
4º resto
5º resto
6º resto
4710 = 1011112
2
11
2
1
5
1
2
2
2
0
1

17. SISTEMA DE NUMERAÇÃO
2.2 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA BINÁRIO
(LSB)
(MSB)
O último quociente será o algarismo mais
significativo e ficará colocado à esquerda.
Os outros algarismos seguem na ordem até
o 1° resto.
4710
=
1011112
O bit menos significativo de um número
binário recebe a notação de LSB (Least
Significant Bit) e o bit mais significativo de
MSB (Most Significant Bit)

18. SISTEMA DE NUMERAÇÃO
2.2 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA BINÁRIO
Façam as conversões dos números decimais mencionados abaixo, para o
para o sistema binário, utilizando o método das divisões sucessivas.
a)
400
b)
21
c)
552
d)
715
e)
27
f)
45
g)
28

19. SISTEMA DE NUMERAÇÃO
2.3 CONVERSÃO NÚMEROS BINÁRIO FRACIONÁRIOS EM DECIMAIS
Seguindo o mesmo método apresentado anteriormente, só que agora, utilizando um
número decimal fracionário qualquer, por exemplo, o número 10,5 e, aplicando a regra
básica de formação de um número, temos:
101 100 10-1
1
0
5
=
(1 x 101) + (0 x 100) + (5 x 10-1) = 10,5
Para números binários, agimos da mesma forma. Vamos transformar em decimal o
número 101,1012.
22 21 20
2-1 2-2 2-3
1
0
1
1
0
1
=
(1 x 22) + (0 x 21) + (1 x 20) + (1 x 2-1) + (0 x 2-2) + (1 x 2-3) =
= x 1/8) = 5,625
4 + 0 + 1 + 0,5 + (0 x ¼) + (1
10
=
101,1012

20. SISTEMA DE NUMERAÇÃO
2.3 CONVERSÃO NÚMEROS BINÁRIO FRACIONÁRIOS EM DECIMAIS
Façam a conversão dos números binários mencionados abaixo, para o
sistema decimal.
a) 1010,11012
b) 111,0012
c) 100,110012

21. SISTEMA DE NUMERAÇÃO
2.4 CONVERSÃO NÚMEROS DECIMAIS FRACIONÁRIOS EM BINÁRIOS
Vamos tomar como exemplo, o número decimal fracionário 8,375 e convertêlo para binário.
Este número significa: 8 + 0,375 = 8,375
1º Passo: Transformar a parte inteira do número, como já vimos
anteriormente:
8
LSB
2
0
4
2
0
2
2
0
1
MSB
810 = 10002

22. SISTEMA DE NUMERAÇÃO
2.4 CONVERSÃO NÚMEROS DECIMAIS FRACIONÁRIOS EM BINÁRIOS
2º Passo: Transformar a parte fracionária, que consiste na multiplicação
sucessiva das partes fracionárias resultantes pela base, até atingir zero. O
número fracionário convertido será composto pelos algarismos inteiros
resultantes tomados na ordem das multiplicações. Teremos então:
1° algarismo
2° algarismo
3° algarismo
0,375
x2
------0,75
x2
------1,5
0,5
x2
------1
Parte fracionária
Base do sistema
Quando atingirmos o número 1, e a parte após a virgula não for nula,
separamos esta última e reiniciamos o processo:
O processo para aqui, pois a parte do número depois da vírgula é nula.

23. SISTEMA DE NUMERAÇÃO
2.4 CONVERSÃO NÚMEROS DECIMAIS FRACIONÁRIOS EM BINÁRIOS
Para finalizar a conversão, efetuamos a composição da parte inteira com a fracionária,
ficando da seguinte forma:
8,37510 = 1000,0112
Exercícios
Façam a conversão dos números decimais fracionários abaixo para o sistema
binário:
a) 4,810
b) 0,62510
c) 3,38010

24. SISTEMA DE NUMERAÇÃO
Faça a conversão do número decimal fracionário 4,810, para o sistema binário.
1. Passo: Transformar a parte inteira do número 410
410 = 1002
2. Passo: Converter a parte fracionária utilizando a regra já aplicada.
a)
b)
c)
d)
0,8 x 2 = 1,6
0,6 x 2 = 1,2
0,2 x 2 = 0,4
0,4 x 2 = 0,8
0,810 = (0,1100 1100 1100...)2
Sequência
calculada
Repetições
Podemos notar que o número 0,8 tornou a aparecer. Se continuarmos o processo,
teremos a mesma sequência já vista até aqui. Um caso equivalente a uma dízima. Temos
então:
Logo: 4,810 = (100,1100110011001100...)2

25. SISTEMA DE NUMERAÇÃO
Faça a conversão do número decimal fracionário 0,62510, para o sistema binário.
a) 0,625 x 2 = 1,250
b) 0,250 x 2 = 0,5
c) 0,5 x 2 = 1 (verdadeiro)
Logo, dizemos que (0,625)10 = (0,101)2

26. SISTEMA DE NUMERAÇÃO
Faça a conversão do número decimal fracionário 3,38010, para o sistema binário.
1. Passo: Transformar a parte inteira do número 310
310 = 112
2. Passo: Converter a parte fracionária utilizando a regra já aplicada.
1)
2)
3)
4)
5)
6)
7)
8)
9)
0,38 x 2 = 0,76
0,76 x 2 = 1,52
0,52 x 2 = 1,04
0,04 x 2 = 0,08
0,08 x 2 = 0,16
0,16 x 2 = 0,32
0,32 x 2 = 0,64
0,64 x 2 = 1,28
0,28 x 2 = 0,56
Neste caso, temos:
0,0110000102 = 1 x 2-2 + 1 x 2-3 + 1 x 2-8 = 0,3789062510
Observação: Se aproximarmos o número decimal em duas casas,
teremos 0,38, logo, para uma precisão de duas casas decimais é
suficiente que tenhamos seguido o método até aí.
0,3810 = 0,011000012 .: 3,3810 = 11,0110000102

27. 3. O Sistema Octal de Numeração

28. SISTEMA DE NUMERAÇÃO
3.1 O SISTEMA OCTAL DE NUMERAÇÃO
O sistema octal de numeração é um sistema de base 8 no qual existem 8 algarismos
assim enumerados:
0, 1, 2, 3, 4 ,5 6 e 7

29. SISTEMA DE NUMERAÇÃO
3.2 CONVERSÃO DO SISTEMA OCTAL PARA O SISTEMA DECIMAL
Para convertermos um número octal em decimal, utilizamos o conceito básico de
formação de um número, conforme já visto.
Vamos converter o número 1448 em decimal:
82
81
80
1
4
4
=
(1 x 82) + (4 x 81) + (4 x 80) = 64 + 32 + 4 = 10010
.: 1448 = 10010

30. SISTEMA DE NUMERAÇÃO
3.2 CONVERSÃO DO SISTEMA OCTAL PARA O SISTEMA DECIMAL
Converta os números abaixo em decimal.
a) 778
b) 1008
c) 4768
d) 218
e) 358

31. SISTEMA DE NUMERAÇÃO
3.3 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA OCTAL
O processo é análogo do sistema decimal do sistema binário. Só que neste
caso utilizaremos a divisão por 8, por ser o sistema octal, sua base é igual a
8.
Exemplo: Convertendo o número 9210 para o sistema octal.
92
4
8
11
8
3
1
9210 = 1348

32. SISTEMA DE NUMERAÇÃO
3.3 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA OCTAL
Converta os números decimais abaixo para o sistema octal.
a) 7410
b) 51210
c) 71910

33. SISTEMA DE NUMERAÇÃO
3.2 CONVERSÃO DO SISTEMA OCTAL PARA O SISTEMA BINÁRIO
Trata-se de uma conversão extremamente simples, podendo-se utilizar a
regra prática descrita abaixo.
Tomemos como exemplo o número octal 278. A regra consiste em transformar
cada algarismo diretamente no seu correspondente em binário, respeitando o
número padrão de bits do sistema, sendo para o octal igual a três (23 = 8.
Desta forma, teremos:
2
010
7
111

34. SISTEMA DE NUMERAÇÃO
3.2 CONVERSÃO DO SISTEMA OCTAL PARA O SISTEMA BINÁRIO
Trata-se de uma conversão extremamente simples, podendo-se utilizar a regra prática
descrita abaixo.
Tomemos como exemplo o número octal 278. A regra consiste em transformar cada
algarismo diretamente no seu correspondente em binário, respeitando o número
padrão de bits do sistema, sendo para o octal igual a três (23 = 8. Desta forma,
teremos:
2
010
7
111

35. SISTEMA DE NUMERAÇÃO
3.2 CONVERSÃO DO SISTEMA OCTAL PARA O SISTEMA BINÁRIO
Converta os números octais em binários:
a) 348
b) 5368
c) 446758
d) 578
e) 258
f)
118
g) 728

36. 4. O Sistema Hexadecimal de
Numeração

37. SISTEMA DE NUMERAÇÃO
4.1 O SISTEMA HEXADECIMAL DE NUMERAÇÃO
O Sistema hexadecimal possui 16 algarismos, sendo sua base igual a 16. Os
algarismos são assim enumerados:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E e F
Notamos que a letra “A” por sua vez representa a quantidade dez. A letra “B”
que representa a quantidade onze, e assim sucede até a letra F, que
representa a quantidade quinze.
Este sistema é muito usado na área de microprocessadores e também no
mapeamento de memoria em sistemas digitais, sendo aplicado em projetos
de software e hardware.

38. SISTEMA DE NUMERAÇÃO
4.1 CONVERSÃO DO SISTEMA HEXADECIMAL PARA O SISTEMA
DECIMAL
A regra de conversão é análoga à de outros sistemas, somente que neste
caso a base é 16.
Exemplo: Converta o número 3F16 em decimal.
161 160
3
F
=
(3 x 161)+ (15 x 160) = 6310
Sendo F16 = 1510

39. SISTEMA DE NUMERAÇÃO
4.1 CONVERSÃO DO SISTEMA HEXADECIMAL PARA O SISTEMA
DECIMAL
Converta os números hexadecimal para decimal:
a) 1C316
b) 23816
c) 1FC916

40. SISTEMA DE NUMERAÇÃO
4.3 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA
HEXADECIMAL
Da mesma forma como nos casos anteriores, esta conversão se faz através
de divisões sucessivas pela base do sistema a ser convertido.
Exemplo: transformar o número 100010 em hexadecimal.
1000
16
8
62
14
16
3
Sendo 1410 = E16
100010 = 3E816

41. SISTEMA DE NUMERAÇÃO
4.3 CONVERSÃO DO SISTEMA DECIMAL PARA O SISTEMA
HEXADECIMAL
Convertam os números decimais abaixo para o sistema hexadecimal.
a) 13410
b) 38410
c) 388210

42. SISTEMA DE NUMERAÇÃO
4.4 CONVERSÃO DO SISTEMA BINÁRIO PARA O SISTEMA
HEXADECIMAL
É análoga à conversão do sistema binário para octal, só que neste caso,
agrupamos de 4 em 4 bits para a esquerda.
Exemplo: Transforme o número 100110002 em hexadecimal.
1001 1000
9
8
.: 100110002 = 9816

43. SISTEMA DE NUMERAÇÃO
4.4 CONVERSÃO DO SISTEMA BINÁRIO PARA O SISTEMA
HEXADECIMAL
Converta para o sistema hexadecimal os números binários:
a) 11000112
b) 110001111000111002

44. SISTEMA DE NUMERAÇÃO
4.5 CONVERSÃO DO SISTEMA HEXA PARA O SISTEMA BINÁRIO
É análoga à conversão do sistema octal para binário, só que neste caso,
necessita-se de 4 bits para representar cada hexadecimal
Exemplo: Converter o número C1316 para o sistema binário:
C  C16 = 1210
C = 1100
1 = 0001
3 = 0011
C1316 = 1100000100112

45. SISTEMA DE NUMERAÇÃO
4.5 CONVERSÃO DO SISTEMA HEXA PARA O SISTEMA BINÁRIO
Exercícios: Convertam os números abaixo para o sistema decima:
a) 1ED16
b) 6CF916