Aula de Logaritmos
- 1. Logaritmos
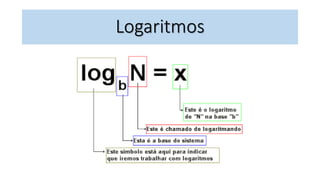
- 2. 3 4 = 81 log3 81 = 4 • 4 é logaritmo (expoente) de 81 na base 3 log 𝑎 𝑏 = 𝑥 Logaritmo logaritmando base • Logaritmo é um número (expoente) a que deve elevar um número tomado como base para se obter outro número.
- 3. Exemplos log5 25 = 𝑥 log2 1 16 = 𝑥 log2 32 = 𝑥 5 𝑥 = 25 5 𝑥 = 52 X = 2 2 𝑥 = 1 16 2 𝑥 = 1 24 2 𝑥 = 2−4 x = -4 2 𝑥 = 32 2 𝑥 = 25 X = 5 log√3 81 = 𝑥 3 𝑥 = 81 3 𝑥 2 = 34 𝑥 2 = 4 x = 4.2 x = 8 Quando as bases estão iguais, pode cortar. Quando invertemos um número, seu expoente fica negativo. Para deixarmos as bases iguais, basta fatorar o outro número e deixar a base dos dois iguais. Toda raiz quadrada, vale dois (√ = 2) e todo número que não tem expoente, tem 1 em cima. (3 = 31 ). Para tirar um número da raiz, colocamos o expoente de dentro para fora. 3 𝑥 3 𝑥 2
- 4. log5 0,000064 (0,000064) = 5 𝑥 64 1.000.000 = 5 𝑥 26 106 = 5 𝑥 ( 2 10 ) = 5 𝑥 1 5 = 5 𝑥 5−6 = 5 𝑥 x = -6 6 6 Contar os números depois da vírgula e transformar em fração. Fatorar Como os dois números estão elevados a 6, basta colocar apenas um expoente 6 fora do parêntese. Simplificar a fração e inverter a fração para as bases ficarem iguais. log2 0,25 = x 2 𝑥 =0,25 2 𝑥 = 25 100 2 𝑥 = 1 4 2 𝑥 = 4−1 2 𝑥 = (2²)−1 X = -2 Transformar 0,25 em fração (dois números depois da vírgula = 100). Simplificar e inverter. fatorar o 4 para ficar igual a base 2 do lado esquerdo. Multiplica-se os expoentes. Exemplos
- 5. Dicas log√3 𝑁 = 2 N = (√3) ² N = 3 Quando há raiz quadrada e expoente dois, pode cortar. log423421 1 = x 423421 𝑥 = 1 x = 0 423421 elevado a 0 vai dar 1. Todo número elevado a zero é 1. log 100 = 𝑥 log10 100 = 𝑥 10 𝑥 = 100 x = 2 Quando a base não aparecer, será sempre 10. 0,0025 = 4 números depois da vírgula = 25 10.000 0,02 = 2 números depois da vírgula = 2 100 O x do log sempre estará depois da igualdade. log2 4 = 𝑥 elevado a
- 6. Exercícios a) log16 64 = 𝑥 b) log5(0,000064) c) log49∛7 d) log 𝑥 9 4 = 2 e) log 10.000 = 𝑥 f) log2 128 = 𝑥 g) log9 81 h) log 𝑏 1 = 𝑥 i) log10 100 = 𝑥 j) log2 1 32 a) log2 8 b) log8 32 c) log4 64 d) log8 32 e) log9 27 f) log8(4 2) g) log27( 9√3) O valor de log1 4 32 é: a) 4 5 b) −2 5 c) 1 5 d) −5 2 e) -1 O resultado de log2 16 − log4 32 é: a) 1 2 b) 3 2 c) 4 d) 1 a) log5 𝑁 = 3 B) log√3 𝑁 = 2 c) log3 𝑁 = 9 d) log 𝑎 81 = 4 e) log 𝑎 10 = 2 f) log9𝑎 27 = 1 2
- 7. Exercícios - Respostas a) 3/2 b) -6 c) 1/6 d) 3/2 e) 4 f) 7 g) 2 h) 0 i) 2 j) -5 a) 3 b) 4 c) 3 d) 5/3 e) 3/2 f) 5/6 g) 5/6 Alternativa: D Alternativa B a) 125 b) 3 c) 27 d) 3 e) √2.5 f) 3
- 8. Propriedades dos logaritmos a) log 𝑎 𝑏. 𝑐 = log 𝑎 𝑏 + log 𝑎 𝑐 b) log 𝑎 𝑏 𝑐 = log 𝑎 𝑏 − log 𝑎 𝑐 c)log √𝑥 𝑎 = log 𝑥 𝑎 2 d) log 𝑎( 𝑏) 𝑐 = C. log 𝑎 𝑏 Multiplicação = adição Divisão = subtração Raiz = fração Expoente = multiplicador
- 9. Exemplos log 0,02 log 2 100 log 2 − log 100 log10 2 − 2 log2 ( 4.16.64 ) log2 4 + log2 16 + log2 64 2 + 4 + 6 12 Sendo log 3 = 1 e log 2 = 5, calcule: log10 1,5 log10 15 10 log10 3 2 log 3 - log 2 1 – 5 -4 log3 92 2. log3 9 2. 3 𝑥 = 9 2.2 4 Sendo: log 𝑏 𝑦 = 3 𝑒 log 𝑏 𝑥 = −4 Calcule: log 𝑏 𝑦. 𝑥2 2log 𝑏 𝑦. 𝑥 2log 𝑏 𝑦 + log 𝑏 𝑥 2.3 + (-4) 6 – 4 2
- 10. Exercícios Sendo log 𝑎 𝑏 = 2 𝑒 log 𝑎 𝑐 = 3, 𝑐𝑎𝑙𝑐𝑢𝑙𝑒 a) log 𝑎 𝑎. 𝑏. 𝑐 b) log 𝑎 ( 𝑎.𝑏 𝑐 ) Assinale a propriedade que está correta: a) log 𝑎. 𝑏 = log 𝑎 . log 𝑏 b) log 𝑎 + 𝑏 = log 𝑎 + log 𝑏 c) log 𝑚. 𝑎 = 𝑚. log 𝑎 d) log 𝑎 𝑚 = log 𝑚. 𝑎 e) log 𝑎 𝑚 = m. log 𝑎 Dado log 2x = 2,4 e log 2 = 0,3, calcule x. Calcular: a)2.log 𝑥 = log 3 + log 4 b) Log a + log b + log c c) Log 6 d) log 𝑎𝑏² 𝑐 e) Log 100 100 f) log4√16
- 11. Exercícios - Respostas a) 6 b) 0 Alternativa E x = 8 a) √12 b) Log (a.b.c) c) Log 2 + log 3 d) 2. log ab – log c e) 0 f)1
- 12. Mudança de base log 𝑐 𝑎 log 𝑏 𝑎 log 𝑏 𝑐 Nova base A nova base aparece em cima e em baixo da divisão. Acompanhado da nova base, aparecem os dois termos que estavam no antigo log. Deixando a velha base por último, em baixo. C > 0 e C ≠ 0
- 13. Exemplos Transformar log4 64 em base 2 log4 64 = log2 64 log2 4 = 6 2 = 3 log2 64 = 2 𝑥 = 26 x = 6 log2 4 = 2 𝑥 = 22 x = 2 Sabendo que log25 = 20 e log27 = 10, resolva log25 . Log72. 20 10 =2
- 14. Exercícios Determine o valor de log50 100, sabendo que log10 5 = a. Se log3 a = x, então log9 a² é igual a: a) 2x² b) x² c) x + 2 d) 2x e) x Calcule log27 z, sabendo que log3 z = w. Supondo que uma máquina de calcular apenas possa determinar logaritmos na base 10, por exemplo, temos log2 = 0,30. Calcular log2 10 .
- 15. Exercícios - Respostas log2 10= 10/3
- 16. Equações logarítmicas log2 𝑥2 + 𝑥 − 4 = 3 Elevado a Igual a log3 3 − 𝑥 = log3(3𝑥 + 7) Cortar apenas quando são dois log, um de cada lado da igualdade. Soma ou subtração: aplicamos as propriedades. 2. log 𝑥 = log 2𝑥 − 3 − log(𝑥 + 2) log 𝑥² = log 2𝑥 − 3 𝑥 + 2 log4 𝑥 + log 𝑥 4 = 2 log4 𝑥 + log 𝑥 log4 4 log4 𝑥 = 2 Trocar de base para poder resolver. Sempre verificar, ou seja, substituir no x.
- 17. Exemplos log x–16 = 1 log x – 1 6 = 1 (x – 1)¹ = 6 x – 1 = 6 x = 6 + 1 x = 7 x – 1 > 0 7 – 1 = 6. S {7} Sempre tem que dar um número maior que zero para entrar na solução. log 5 (x + 2) = 2 log 5 (x + 2) = 2 x + 2 = 5² x + 2 = 25 x = 25 – 2 x = 23 x + 2 > 0 23 - 2 = 21 S {23} log2x + log2 (x – 2) = log28 log2x + log2 (x – 2) = log28 log2 x . (x – 2) = log28 x . (x – 2) = 8 x² – 2x – 8 = 0 ∆ = -2² - 4. 1. -8 = 36 x = -2² +/- 6 2. 1 X-2 > 0 x-2 > 0 4-2 = 2 -2 -2 = 0 S { 4} 4 -2 V VV F
- 18. Exercícios a) log 3 (x + 5) = 2 b) log (3+x) (x2 – x) = 1 c) log 2 (4x + 5) = log 2 (2x + 11) 01) O conjunto solução da equação logarítmica é: (A) {-1; 2} (B) {-2; 1} (C) {-2} (D) {1} (E) { } 4) (UFRGS) A solução da equação está no intervalo: (A) [-2; -1] (B) (-1; 0] (C) (0; 1] (D) (1; 2] (E) (2; 3]
- 19. Exercícios - Respostas a) S = {4} b) S = {-1,3} c) S = {-4, 3} (B) {-2; 1} (C) (0; 1]
- 20. •FIM
