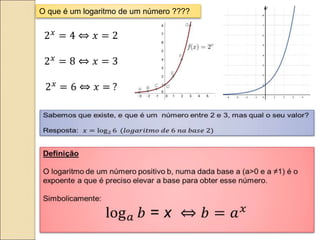
O documento explica o que é um logaritmo e como calculá-lo. Apresenta exemplos de como calcular logaritmos de números, utilizando as propriedades do logaritmo do produto, quociente e potência. Demonstra também como resolver problemas financeiros utilizando logaritmos.

1. O que é um logaritmo de um número ????

7. 1º Exemplo – Matemática Financeira
Uma pessoa aplicou a importância de R$ 500,00 em uma instituição
bancária, que paga juros mensais de 3,5%, no regime de juros
compostos. Quanto tempo após a aplicação o montante será de R$ 3
500,00?
Fórmula para o cálculo dos juros
compostos: M = C·(1 + i)t. De
acordo com a situação-problema,
temos:
Aplicando o logaritmo:
t·0,0149 = 0,8451
t = 0,8451 /
0,0149
t = 56,7
log 1,035t = log 7
t·log 1,035 = log
7 utilize tecla log da
calculadora científica
O montante de R$ 3
500,00 será originado
após 56 meses de
aplicação.

8. Logaritmo
Definição de logaritmo
Lê-se logaritmo de b na base a.
Condição de existência :
a > 0 a ≠ 1 b > 0
Quando a base de um logaritmo for omitida, significa que seu
valor é igual a 10. Este tipo de logaritmo é chamado de
logaritmo decimal.

9. Exemplos
Qual o valor do log3 81?
Solução
Neste exemplo, queremos descobrir qual expoente devemos elevar o 3
para que o resultado seja igual a 81.
Usando a definição, temos: log3 81 = x ⇔ 3x = 81
Para encontrar esse valor, podemos fatorar o
número 81, conforme indicado abaixo:
Substituindo o 81 por sua forma fatorada, na equação anterior, temos:
3x = 34
Como as bases são iguais, chegamos a conclusão que x = 4.

10. Exemplos

11. Exemplos

12. Consequências da definição
O logaritmo de qualquer base, cujo logaritmando seja igual a 1, o
resultado será igual a 0, ou seja, loga 1 = 0.
Exemplo, log9 1 = 0, pois 90 =1.
Quando o logaritmando é igual a base, o logaritmo será igual a 1,
assim, loga a = 1.
Exemplo, log5 5 = 1, pois 51= 5
Quando o logaritmo de a na base a possui uma potência m, ele
será igual ao expoente m, ou seja loga am = m, pois usando a
definição am = am.
Exemplo, log3 35 = 5.

13. Propriedades dos logaritmos

14. Logaritmo do Produto
Exemplo: Dados log2 = 0,301 e log3 = 0,477, determine o log12.
log12 → log12 = log (2·2·3) Reescrevendo 12
Log12 = log2 + log2 + log3
0,301 + 0,301 + 0,477 Substituindo pelos valores conhecidos
log 12 = 1,079

15. Logaritmo do Produto
Exemplo : Determine o valor de log2 (8·32)
Log2(8·32) = log28 + log232 Calculando os logs
3 5
Log2(8·32) = 3 + 5 = 8

16. Logaritmo do Quociente
Exemplo :
Sabendo que log30 = 1,477 e log5 = 0,699, determine log 6.
log6 = (30/5) Reescrevendo 6
log30 – log5 = 1,477 – 0,699 Substituindo pelos valores conhecidos
log6 = 0,778

17. Logaritmo do Quociente
Exemplo :
Assumindo que log2=0,3 e log10=1 . Calcule log5
log5= log10 / log2 Reescrevendo 5
Log5 = log10 – log 2 Aplicando a propriedade
Log 5 = 1 – 0,3 Substituindo pelos valores conhecidos
Log 5 = 0,7

18. Logaritmo da Potência
Exemplo:
Sabendo que log 2 = 0,3010 . Calcule o valor de log 64.
log 64 = log 26 Reescrevendo 64
log 64 = 6·log 2 Aplicando a propriedade
log64 = 6·0,3010 Substituindo pelos valores conhecidos
log64= 1,806

19. Logaritmo da Potência
Exemplo:
Considerando log 3 = 0,48, determine o valor do log 81.
Podemos escrever o número 81 como sendo 34. Neste caso,
vamos aplicar a propriedade do logaritmo de uma potência, ou
seja:
log 81 = log 34
log 81 = 4 . log 3
log 81 = 4 . 0,48
log 81 = 1,92