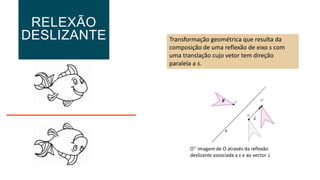
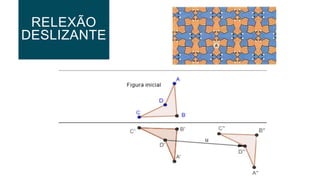
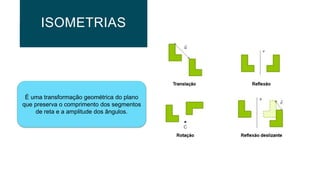
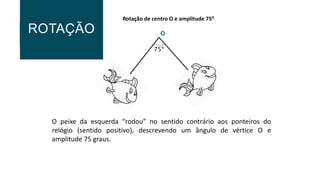
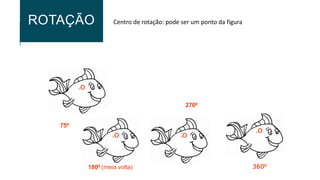
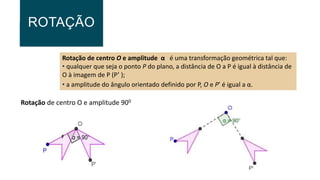
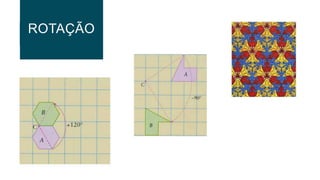
O documento descreve três tipos de isometrias geométricas: rotação, reflexão e translação. Rotação preserva comprimentos e ângulos e envolve girar uma figura em torno de um ponto. Reflexão envolve refletir uma figura sobre uma reta. Translação envolve deslocar uma figura na mesma direção e distância, preservando comprimentos e ângulos.

1. ISOMETRIAS TIPOS DE ISOMETRIAS

2. ISOMETRIAS
É uma transformação geométrica do plano
que preserva o comprimento dos segmentos
de reta e a amplitude dos ângulos.

3. ROTAÇÃO
75º
O peixe da esquerda “rodou” no sentido contrário aos ponteiros do
relógio (sentido positivo), descrevendo um ângulo de vértice O e
amplitude 75 graus.
Rotação de centro O e amplitude 750
O

4. ROTAÇÃO
.O
750
.O
3600
Centro de rotação: pode ser um ponto da figura
1800 (meia volta)
.O
.O
2700

5. ROTAÇÃO
Rotação de centro O e amplitude α é uma transformação geométrica tal que:
• qualquer que seja o ponto P do plano, a distância de O a P é igual à distância de
O à imagem de P (P’ );
• a amplitude do ângulo orientado definido por P, O e P’ é igual a α.
Rotação de centro O e amplitude 900
F

6. ROTAÇÃO

7. REFLEXÃO
Cada ponto de uma figura e a sua imagem estão sobre uma reta
perpendicular ao eixo de reflexão e a igual distância desse eixo.
É como se o peixe e a estrela se estivessem “a ver ao espelho”...
Os eixos de reflexão podem, ou não ter pontos em comum com
a(s) figura(s)
eixo de reflexão

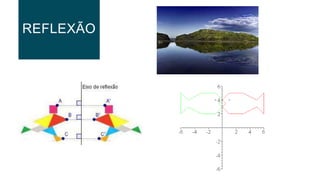
8. REFLEXÃO
Reflexão de eixo s é a transformação geométrica que faz corresponder a cada
ponto O do plano o ponto O’ (imagem de O) de tal modo que:
•a reta s é perpendicular a [O O’] e passa pelo ponto médio de [O O’] (ou s é a
mediatriz de [O O’];
•se O pertence a s, a sua imagem coincide com O.
 Reflexão da figura F de de eixo s
s
F

9. REFLEXÃO

10. TRANSLAÇÃO
Numa translação todos os pontos de uma figura se “deslocam” na
mesma direção, no mesmo sentido e a mesma distância.

u

v
Translação associada ao vetor

u
Translação associada ao vetor

v

11. TRANSLAÇÃO
Translação associada ao vetor é uma transformação geométrica em que cada
ponto O do plano é transformado num outro ponto O’ (imagem de O) em que
O’ = O +
u

u

F
 Translação da figura F associada ao
vetor u

u


12. TRANSLAÇÃO

13. RELEXÃO
DESLIZANTE Transformação geométrica que resulta da
composição de uma reflexão de eixo s com
uma translação cujo vetor tem direção
paralela a s.
O’’ imagem de O através da reflexão
deslizante associada a s e ao vector
s
u

u

F

14. RELEXÃO
DESLIZANTE

15. APLICAR
-Resolver:
• os exercícios das páginas
34 e 35, do volume 1