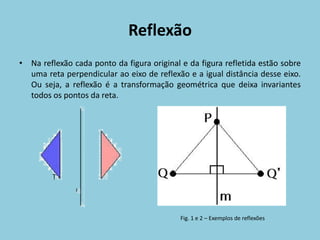
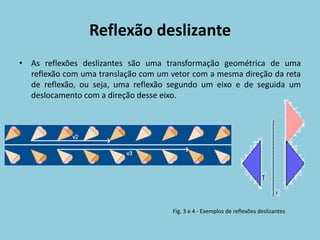
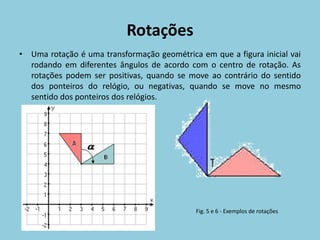
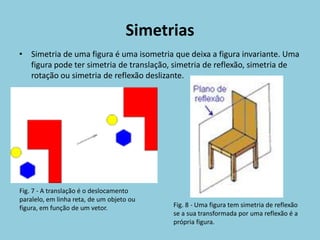
O documento discute os conceitos de isometrias, incluindo reflexão, reflexão deslizante, rotação, simetrias e padrões. Exemplos ilustram como essas transformações geométricas preservam distâncias e ângulos. Rosáceas, frisos e pavimentações são discutidos como aplicações dessas isometrias.

1. Isometrias
Trabalho realizado por: Catarina Soares, Filipe
Machado, Filipe Gordinho e Francisco Fernandes

2. Isometrias
• Isometria é uma transformação geométrica que mantém a distância entre
pontos e preserva ângulos, isto é, a figura inicial e a transformada são
congruentes. Existem 4 isometrias: a translação, a rotação, a reflexão e a
reflexão deslizante.

3. Reflexão
• Na reflexão cada ponto da figura original e da figura refletida estão sobre
uma reta perpendicular ao eixo de reflexão e a igual distância desse eixo.
Ou seja, a reflexão é a transformação geométrica que deixa invariantes
todos os pontos da reta.
Fig. 1 e 2 – Exemplos de reflexões

4. Reflexão deslizante
• As reflexões deslizantes são uma transformação geométrica de uma
reflexão com uma translação com um vetor com a mesma direção da reta
de reflexão, ou seja, uma reflexão segundo um eixo e de seguida um
deslocamento com a direção desse eixo.
Fig. 3 e 4 - Exemplos de reflexões deslizantes

5. Rotações
• Uma rotação é uma transformação geométrica em que a figura inicial vai
rodando em diferentes ângulos de acordo com o centro de rotação. As
rotações podem ser positivas, quando se move ao contrário do sentido
dos ponteiros do relógio, ou negativas, quando se move no mesmo
sentido dos ponteiros dos relógios.
Fig. 5 e 6 - Exemplos de rotações

6. Simetrias
• Simetria de uma figura é uma isometria que deixa a figura invariante. Uma
figura pode ter simetria de translação, simetria de reflexão, simetria de
rotação ou simetria de reflexão deslizante.
Fig. 7 - A translação é o deslocamento
paralelo, em linha reta, de um objeto ou
figura, em função de um vetor. Fig. 8 - Uma figura tem simetria de reflexão
se a sua transformada por uma reflexão é a
própria figura.

7. Rosáceas
• A rosácea é um elemento arquitetónico plano que possui um número
finito de simetrias de rotação e de reflexão.
Fig. 9 e 10 - Exemplos de rosáceas

8. Frisos
• Um friso é uma figura plana que possui uma infinidade de simetrias de
translação. Os vetores associados a essas translações possuem todos a
mesma direção e são múltiplos inteiros de um dado vetor não nulo.
Fig. 11 – Exemplo de um friso

9. Padrões
• Um padrão é a repetição regular de uma figura inicial obedecendo a uma
determinada disposição que caracteriza esse padrão.
Fig. 12 e 13 – Exemplos de padrões

10. Classificação de padrões
• Os padrões classificam-se em dezassete tipos diferentes, cada um deles
relacionado com um grupo de simetria. Esta classificação é feita através de
tipos de simetria que cada padrão contém.
Fig. 14 - Contém reflexões deslizantes e rotações de
180º. Os centros de rotação não se encontram nos
eixos de reflexão que são perpendiculares.
Fig. 15 - Contém rotações de 90º e de 180º. Os
centros de rotação de 180º estão entre os centros de
rotação de 90º.

11. Pavimentações
• É um conjunto de mosaicos ou ladrilhos que cobrem o plano sem espaços
intermédios nem sobreposições.
Fig. 16 - Exemplo de pavimentações
típicas portuguesas

12. Referências Bibliográficas
• http://blogmatematic.blogspot.pt/2012/01/isometrias-reflexao-rotacao-e.html
• http://www.educ.fc.ul.pt/icm/icm99/icm12/introducao.htm
• http://catiaosorio.wordpress.com/2011/02/22/um-pouco-de-matematica-frisos/