1. O documento descreve métodos para determinar a interseção de uma reta com sólidos como cones, cilindros e esferas. 2. Para cones e cilindros, é necessário definir um plano auxiliar que produza uma seção triangular ou paralelográmica para determinar os pontos de interseção. 3. Para esferas, basta lembrar que qualquer plano secante produz uma circunferência de interseção.

1. GEOMETRIA
DESCRITIVA-A
Interseção de retas com Sólidos
_Cones, Cilindros e Esferas
11º Ano
E@D

2. Interseção de uma Reta com um Sólidos - Cones
GEOMETRIA
DESCRITIVA-A
V
X
A interseção de uma reta com o
Cone é o segmento de reta [XY].
Ou seja, os pontos designados por
X e Y, que correspondem aos
pontos de interseção da reta com
o sólido.
s
Y
Excetuando algumas situações
particulares, nos problemas de
interseção de uma retas com cone
não é aconselhável utilizar como
plano auxiliar um dos o planos
projetantes da reta.
Assim deve recorrer-se a um
plano auxiliar que produza no
cone uma secção triangular. Para
que tal possa acontecer esse
plano contém a reta e o vértice

3. Método geral para determinar a Interseção de uma Reta com um Cone
GEOMETRIA
DESCRITIVA-A
1. Definir um plano auxiliar que contenha
a reta dada e o vértice do cone – este
plano produzirá uma secção triangular no
sólido, sendo o vértice do cone um dos
vértices do triângulo. Assim, por um ponto P de s
traçar uma reta p que contenha o vértice do cone V ou
que contenha V e seja paralela a s;
V
p
i
N
α
s
I
g’
Y
g
I’
P
X
M
2. Determinar a reta i de interseção do plano
auxiliar com o plano da base do cone. Para tal
determina-se o ponto de intersecção da reta s com o
plano da base do cone – o ponto I, e, determina-se o
ponto de intersecção da reta p com o plano da base do
cone – o ponto I’, a reta i fica definida pelos pontos I e I’;
4. Os pontos de interseção da reta dada com
figura da secção [MVN] – pontos X e Y são
os pontos de entrada e de saída da reta
dada no sólido.
3. A reta i intersecta a circunferência que
limita a base do cone em dois pontos M e
N – estes serão os outros dois vértices do triângulo
da secção [MVN].

4. Método geral para determinar a Interseção de uma Reta com um - Cone
GEOMETRIA
DESCRITIVA-A
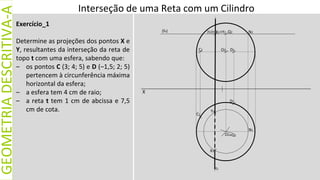
Exercício_1
Determine as projeções dos pontos X
e Y, resultantes da interseção da reta
r com o cone de revolução e base
contida num plano frontal, sabendo
que:
– o ponto O (0; 2; 4) é o centro da
base que é tangente ao plano
horizontal de projeção;
– o cone tem 7 cm de altura;
– a reta r contém o ponto R (0; 5; 6)
e é paralela ao β2.4;
– a projeção horizontal da reta r faz
um ângulo de 30º, de abertura
para a direita, com o eixo x.
X
O2
O1
V1
≡V2
I’1
(hϕ)
P2
r2
P1
s2
s1
r1
I’2
R2
N2
M2
i2
I2
I1
X1
Y1
M1 N1
R1
Y2
X2
≡i1
P + V = s
I + I’= i
ꓵ de r com [VM]= X
ꓵ de r com [VN]= Y

5. Método geral para determinar a Interseção de uma Reta com um - Cone
GEOMETRIA
DESCRITIVA-A
Exercício_2
É dado um cone obliquo, situado no
1º Diedro e com a base contida no
Plano Frontal de Projeção.
– O (3; 0; 4) é o centro da
circunferência que limita a base,
que tem 3,5 cm de raio.
– V (–2; 7; 7) é o vértice do cone.
– É dada uma reta r, oblíqua, que
contém o ponto T (5; 4; 5). A reta
r é paralela ao β1.3 e a sua
projeção frontal faz um ângulo de
30º (a.e.) com o eixo X.
Determine as projeções dos pontos
de intersecção da reta com o sólido e
assinale convenientemente as
visibilidades/invisibilidades da reta.

6. Método geral para determinar a Interseção de uma Reta com um - Cone
GEOMETRIA
DESCRITIVA-A
Exercício_3
É dado um cone reto situado no 1º
Diedro e com a base contida no plano
XY (ν0).
– o cone tem 6 cm de altura e a sua
base tem 3 cm de raio;
– o centro da base é o ponto O (0;
4; 0).
– é dada ainda uma reta horizontal
(de nível) h que contém o ponto A
(– 4; 7; 3) e que faz um ângulo de
45º (a.d.) com o plano XZ (ϕ0).
Determine os pontos E e S,
respetivamente, pontos de entrada e
de saída da reta h, no sólido e
assinale convenientemente as
visibilidades/invisibilidades da reta.

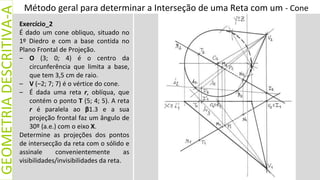
7. A interseção de uma reta com um
Cilindro é o segmento de reta
[XY]. Ou seja, os pontos
designados por X e Y, que
correspondem aos pontos de
interseção da reta com o sólido.
À semelhança dos cones também
no caso dos cilindros é
fundamental que escolha do um
plano auxiliar que produza uma
secção de construção rigorosa.
Interseção de uma Reta com um Cilindro
GEOMETRIA
DESCRITIVA-A
Assim o plano auxiliar deve
produzir no cilindro uma
circunferência ou paralelogramo.
N
M
M’
N’
e
g
X
Y
g’
r

8. GEOMETRIA
DESCRITIVA-A
i
N
I
I’
M
M’
N’
p
e
g
Y
r
1. Definir um plano auxiliar que contenha
a reta dada e a direção do eixo do
cilindro (direção das geratrizes) – a
secção que este plano produzirá no sólido
será um paralelogramo. Assim, por um ponto P de
r traçar uma reta p paralela ao eixo e;
2. Determinar a reta i de interseção do plano
auxiliar com o plano de uma das bases do
cilindro. Para tal determina-se o ponto de intersecção
da reta r com o plano da base – o ponto I, e, determina-
se o ponto de intersecção da reta p com o plano da base
do cilindro – o ponto I’. A reta i fica definida pelos pontos
I e I’;
4. Os pontos de interseção da reta dada com
figura da secção [MM´NN’] – pontos X e Y
são os pontos de entrada e de saída da
reta dada no cilindro.
3. A reta i intersecta a circunferência que
limita a base do cilindro em dois pontos
M e N – estes serão dois vértices do
paralelogramo (figura da secção) e pelas geratrizes
correspondestes [MM’NN’].
P
α
g’
X
Método geral para determinar a Interseção de uma Reta com um - Cilindro

9. X
GEOMETRIA
DESCRITIVA-A
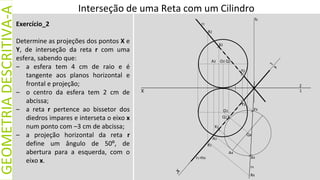
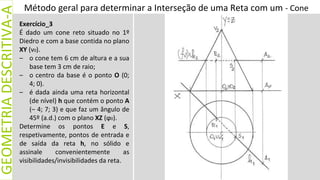
Exercício_1
Determine as projeções dos pontos X
e Y, resultantes da interseção da reta
r com o cilindro de revolução,
sabendo que:
– as bases do cilindro têm 4 cm de
raio e estão contidas em planos
horizontais;
– o ponto O (–1; 6; 2) é o centro da
base de menor cota;
– o centro da outra base pertence
ao bissetor dos diedros impares;
– a reta r contém o ponto A (1; 5; 4)
e B do eixo x, com 7 cm de
abcissa.
(fν)
(f’ν)
O1
r2
M1
N1≡N’1
≡M’1
M’2 N’2
N2
M2
A1
A2
X2
Y2
P1
X1≡
Y1
O2
O’2
≡O’1
B2≡B1
(p1)≡
p2
I’1≡
I’2
P2
I2
I1
r1≡i1
≡i2
P + // [OO’] = p
ꓵ de r c/. (fν) = I
ꓵ de r2 c/. [M’2N’2] = Y2
ꓵ de r2 c/. [M’2M2] = X2
ꓵ de p c/. (fν) = I’
Interseção de uma Reta com um Cilindro
I + I’ = i

10. GEOMETRIA
DESCRITIVA-A
Exercício_2
É dado um cilindro oblíquo, situado
no 1º Diedro e com 8 cm de altura.
Uma das bases está contida no Plano
Horizontal de Projeção, é tangente
ao Plano Frontal de Projeção e o seu
centro é o ponto O (2; 3; 0). As
projeções do eixo do cilindro fazem,
com o eixo X, ângulos de 70º (a.d.) e
30º (a.d.), respetivamente a projeção
frontal e a horizontal.
Determine as projeções dos pontos E
e S de entrada e de saída de uma
reta f, frontal, no sólido, sabendo
que f contém o ponto A (–3; 5; 2) e
faz, com o plano XY (ν0), um ângulo
de 30º (a.e.). Assinale as
invisibilidades da reta.
Interseção de uma Reta com um Cilindro

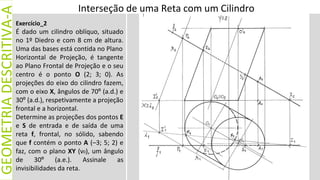
11. A interseção de uma reta com
uma Esfera é o segmento de reta
[XY]. Ou seja, os pontos
designados por X e Y, que
correspondem aos pontos de
interseção da reta com o sólido.
Contudo, é bastante mais simples
do que nas situações anteriores.
Interseção de uma Reta com uma Esfera
GEOMETRIA
DESCRITIVA-A
Assim, na resolução de problemas
de intersecção de retas com
esferas é basta ter sempre
presente que qualquer plano
secante à esfera secciona o
sólido segundo uma
circunferência.
r
X
Y
O

12. X
GEOMETRIA
DESCRITIVA-A
Exercício_1
Determine as projeções dos pontos X e
Y, resultantes da interseção da reta de
topo t com uma esfera, sabendo que:
– os pontos C (3; 4; 5) e D (–1,5; 2; 5)
pertencem à circunferência máxima
horizontal da esfera;
– a esfera tem 4 cm de raio;
– a reta t tem 1 cm de abcissa e 7,5
cm de cota.
(fν) N2
N1
Y1
Q2
O2
O1
X2
(t2)≡
t1
Interseção de uma Reta com um Cilindro
D1
C1
C2
X1
≡Y2
D2
≡Q1

13. X
GEOMETRIA
DESCRITIVA-A
Exercício_2
Determine as projeções dos pontos X e
Y, de interseção da reta r com uma
esfera, sabendo que:
– a esfera tem 4 cm de raio e é
tangente aos planos horizontal e
frontal e projeção;
– o centro da esfera tem 2 cm de
abcissa;
– a reta r pertence ao bissetor dos
diedros impares e interseta o eixo x
num ponto com –3 cm de abcissa;
– a projeção horizontal da reta r
define um ângulo de 50º, de
abertura para a esquerda, com o
eixo x.
Interseção de uma Reta com um Cilindro
O2
O1
r2
A2
X2
Q2
Y2
R2
Q1
Y1
X1
R1
A1
r1≡hδ
r4
X4
R4
Q4
Y4
1
2
fδ
A4

14. GEOMETRIA
DESCRITIVA-A
Exercício_3
Determine as projeções dos pontos
X e Y, de interseção da reta de perfil
p com uma esfera, sabendo que:
– o ponto O (2; 4; 5) é o centro da
esfera;
– a esfera é tangente a ao plano
frontal de projeção;
– a reta p é definida pelo ponto R
(0; 5; 3,5) e pelo seu traço
horizontal com 9 cm de
afastamento.
Interseção de uma Reta com um Cilindro