O documento descreve diferentes tipos de isometrias geométricas como reflexões, reflexões deslizantes, rotações e simetrias. Também explica conceitos como frisos, rosáceas e diferentes tipos de pavimentações como puras, regulares, semi-regulares e periódicas.

2. Isometrias ……………………………………………………………………… Slide
4;5
Reflexões…………………………………………………………………………..
Slide 6
Reflexões deslizantes…...………………………………………………………....
Slide 7
Rotações………………………………………………………………………… Slide
8;9
Simetrias…............................................................................................................
........ Slide 10;11
Frisos……………………………………………………………....…....……….. Slide
12
Rosáceas……………………………………………………………..........Slide 13,
14, 15

3. Índice
Pavimentações……………………………………………Slide
17;18;19;20;21;22;23

4. Isometria – é uma transformação em que o comprimento dos segmentos
de reta e a amplitude dos ângulos que se mantêm.
Fonte - http://www.slideshare.net/jorpereira/rotaoes-isometrias

5.  Rotações  Reflexão
 Translação  Reflexão deslizante
Fonte - http://baudamatematica.wordpress.com/2011/09/30/isometrias/

6. Uma reflexão deslizante é uma transformação geométrica que consiste:
• Numa reflexão seguida de uma translação na direção do eixo de reflexão;
OU
• Numa translação seguida de uma reflexão com eixo paralelo à direção da
translação.
Fonte - https://sites.google.com/site/desmatematicos/videos/8o-ano/translacao-
rotacao-reflexao-reflexao-deslizante-e-simetrias

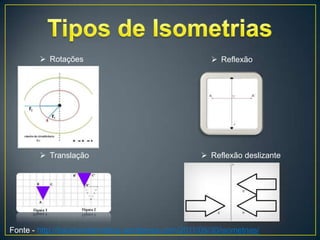
7. Reflexões - Reflexão de eixo r, Rr , é a transformação geométrica que
deixa invariantes todos os pontos da letra r e que, a cada ponto P que
não pertença a r faz corresponder a um ponto P’, chamado transformado
de P tal que:
• A distância de P ao eixo r é igual à distância de P’ ao eixo r,
• [PP’] é perpendicular ao eixo r.
Fonte - https://sites.google.com/site/desmatematicos/videos/8o-ano/translacao-
rotacao-reflexao-reflexao-deslizante-e-simetrias

8. Rotações – rotação de centro O e amplitude é a α, RO,α
transformação geométrica que, ao ponto O faz corresponder o próprio O e a
cada ponto P, diferente de O, faz corresponder um ponto P’, a que se chama
transformado de P, tal que:
Fonte – Matematicamente Falando 8 – págs. 8

9. Se a rotação for feita no sentido contrário aos ponteiros do relógio
(esquerda), define-se sentido positivo.
Se a rotação for feita no sentido dos
ponteiros do relógio (direita), define-se
sentido negativo.
Se uma rotação tiver uma amplitude de
180º, define-se meia-volta.
Fonte – Matematicamente Falando 8 – págs. 9

10. Simetria - A simetria de uma figura é um tipo de isometria que deixa a
figura invariante.
Com a simetria se obtém uma forma de outra preservando suas
características tais como ângulos, comprimento dos lados, distância,
tipos e tamanhos.
Fonte - Matematicamente Falando 8- pág.9;
http://belasimetrias.wordpress.com/2008/02/20/a-simetria-na-matematica/

11.  Simetria de  Simetria de reflexão
translação
 Simetria de rotação
 Simetria de reflexão
deslizante
Fonte – Matematicamente Falando 8 pág. 9

12. Friso - é uma banda com um padrão que se repete
indefinidamente e onde existem simetrias de translação,
todas com uma única direção (geralmente horizontal).
Fonte - http://catiaosorio.wordpress.com/2011/02/22/um-pouco-de-matematica-
frisos/

13. As rosáceas são elementos como os frisos e os
padrões, com a particular diferença de serem figuras
limitadas com a forma de circunferência.
Fonte - http://pt.scribd.com/doc/14999346/rosaceas

14. Existem dois tipos de rosáceas - as
Cíclicas e as Diedrais.
As rosáceas cíclicas não têm eixos de
simetria.
Fonte - http://pt.scribd.com/doc/14999346/rosaceas

15. As rosáceas diedrais têm pelo menos um eixo.
Normalmente são simetrias d rotação.
Fonte - http://pt.scribd.com/doc/14999346/rosaceas

16. Padrão (ou mosaico) - em matemática utiliza-se a palavra padrão
para indicar um desenho plano que se repete periodicamente mais
do que uma direção (ou seja: um desenho para o qual existem
duas translações, em direções diferentes, que mantêm invariante
a estrutura do padrão).
Fonte - http://www.atractor.pt/simetria/matematica/caixas/

17. Uma pavimentação dum plano é um conjunto numerável da ladrilhos que
cobrem o plano sem espaços intermédios nem sobreposições.
Imagem tirada por um elemento do
grupo
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm

18. • Pavimentações puras
• Pavimentações regulares
• As que não são consideradas regulares
• Pavimentações semi-regulares
• Pavimentações periódicas
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm

19. • As pavimentações puras são formadas por um único
ladrilho.
NOTA:
Um Ladrilho é uma lajota
geralmente de forma retangular, feita
em barro, ou de cimento e areia
prensada e é usada em
Pavimentações.
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm

20. • São Pavimentações em que os ladrilhos são polígonos
regulares e congruentes, ou seja, com o mesmo
tamanho e forma.
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm

21. • Estas não são consideradas pavimentações regulares
porque todas elas têm em que cada vértice um que
concorre pelos menos a um dos lados do polígono.
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm

22. • São Pavimentações constituídas por dois ou mais
polígonos regulares em que os vértices da sua
pavimentação são todos do mesmo tipo.
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm

23. • São pavimentações que quando sofrem uma translação
permanecem invariáveis, isto é, podem deslocar-se
sobre si própria, continuando os ladrilhos perfeitamente
alinhados.
Fonte - http://www.educ.fc.ul.pt/icm/icm2003/icm22/tiposdepavimentacao1.htm