1) O documento discute movimentos de translação, propriedades geométricas de translações e representação de translações por vetores.
2) Uma translação é definida como o deslocamento paralelo de todos os pontos de uma figura em uma direção e sentido específicos.
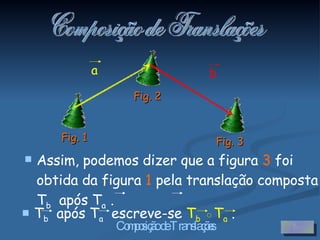
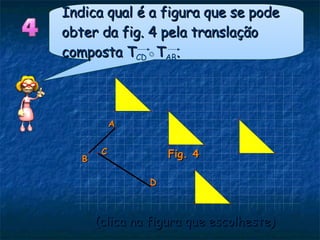
3) A composição de duas translações pode ser representada por uma única translação, onde o vetor resultante é a soma dos vetores individuais.