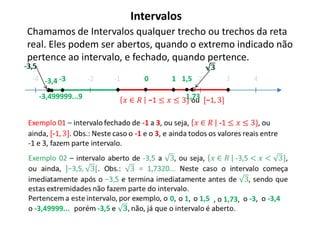
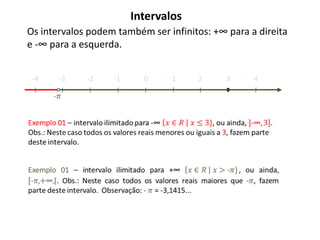
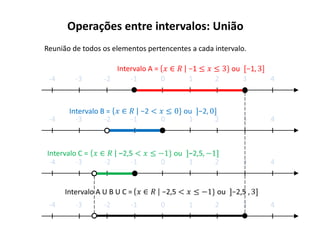
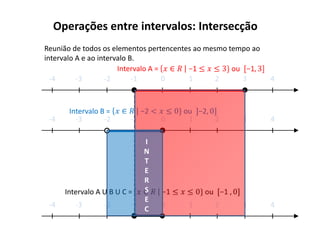
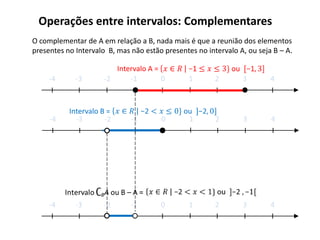
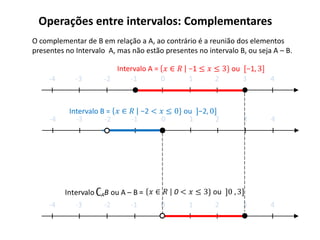
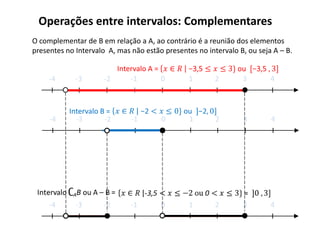
O documento descreve os intervalos reais, incluindo a representação gráfica dos números reais na reta real de forma crescente da esquerda para a direita, e define intervalos como trechos da reta real que podem ser abertos ou fechados. Também apresenta operações entre intervalos como união, interseção e complementares.

1. Intervalos Reais
Prof. Glauber

2. Reta Real
• A reta real é uma representação gráfica do conjunto
dos números reais de forma crescente da esquerda
para a direita.
-4 -2,8888... -2 0 1 3,1 4,22222...
• O zero é chamado de origem. Quanto mais os valores
se distanciam à direita, mais crescem e à esquerda
diminuem.
• Todos os valores pertencentes a este conjunto (IR),
podem ser representados na reta.

3. Intervalos
Chamamos de Intervalos qualquer trecho ou trechos da reta
real. Eles podem ser abertos, quando o extremo indicado não
pertence ao intervalo, e fechado, quando pertence.
-3,5
-4 -3,4 -3 -2 -1 0 1 1,5 2 3 4
-3,499999...9 1,73
0, o 1, o 1,5 , o 1,73, o -3, o -3,4
o -3,49999...

4. Intervalos
Os intervalos podem também ser infinitos: +∞ para a direita
e -∞ para a esquerda.
-4 -3 -2 -1 0 1 2 3 4

5. Operações entre intervalos: União
Reunião de todos os elementos pertencentes a cada intervalo.
Intervalo A =
-4 -3 -2 -1 0 1 2 3 4
Intervalo B =
-4 -3 -2 -1 0 1 2 3 4
Intervalo C =
-4 -3 -2 -1 0 1 2 3 4
Intervalo A U B U C =
-4 -3 -2 -1 0 1 2 3 4

6. Operações entre intervalos: Intersecção
Reunião de todos os elementos pertencentes ao mesmo tempo ao
intervalo A e ao intervalo B.
Intervalo A =
-4 -3 -2 -1 0 1 2 3 4
Intervalo B =
-4 -3 -2 -1 0 1 2 3 4
I
N
T
E
R
Intervalo A U B U C = S
E
-4 -3 -2 -1 0 1 2 3 4
C

7. Operações entre intervalos: Complementares
O complementar de A em relação a B, nada mais é que a reunião dos elementos
presentes no Intervalo B, mas não estão presentes no intervalo A, ou seja B – A.
Intervalo A =
-4 -3 -2 -1 0 1 2 3 4
Intervalo B =
-4 -3 -2 -1 0 1 2 3 4
-4 -3 -2 -1 0 1 2 3 4

8. Operações entre intervalos: Complementares
O complementar de B em relação a A, ao contrário é a reunião dos elementos
presentes no Intervalo A, mas não estão presentes no intervalo B, ou seja A – B.
Intervalo A =
-4 -3 -2 -1 0 1 2 3 4
Intervalo B =
-4 -3 -2 -1 0 1 2 3 4
-4 -3 -2 -1 0 1 2 3 4

9. Operações entre intervalos: Complementares
O complementar de B em relação a A, ao contrário é a reunião dos elementos
presentes no Intervalo A, mas não estão presentes no intervalo B, ou seja A – B.
Intervalo A =
-4 -3 -2 -1 0 1 2 3 4
Intervalo B =
-4 -3 -2 -1 0 1 2 3 4
-4 -3 -2 -1 0 1 2 3 4

10. FUIZZZZ!!