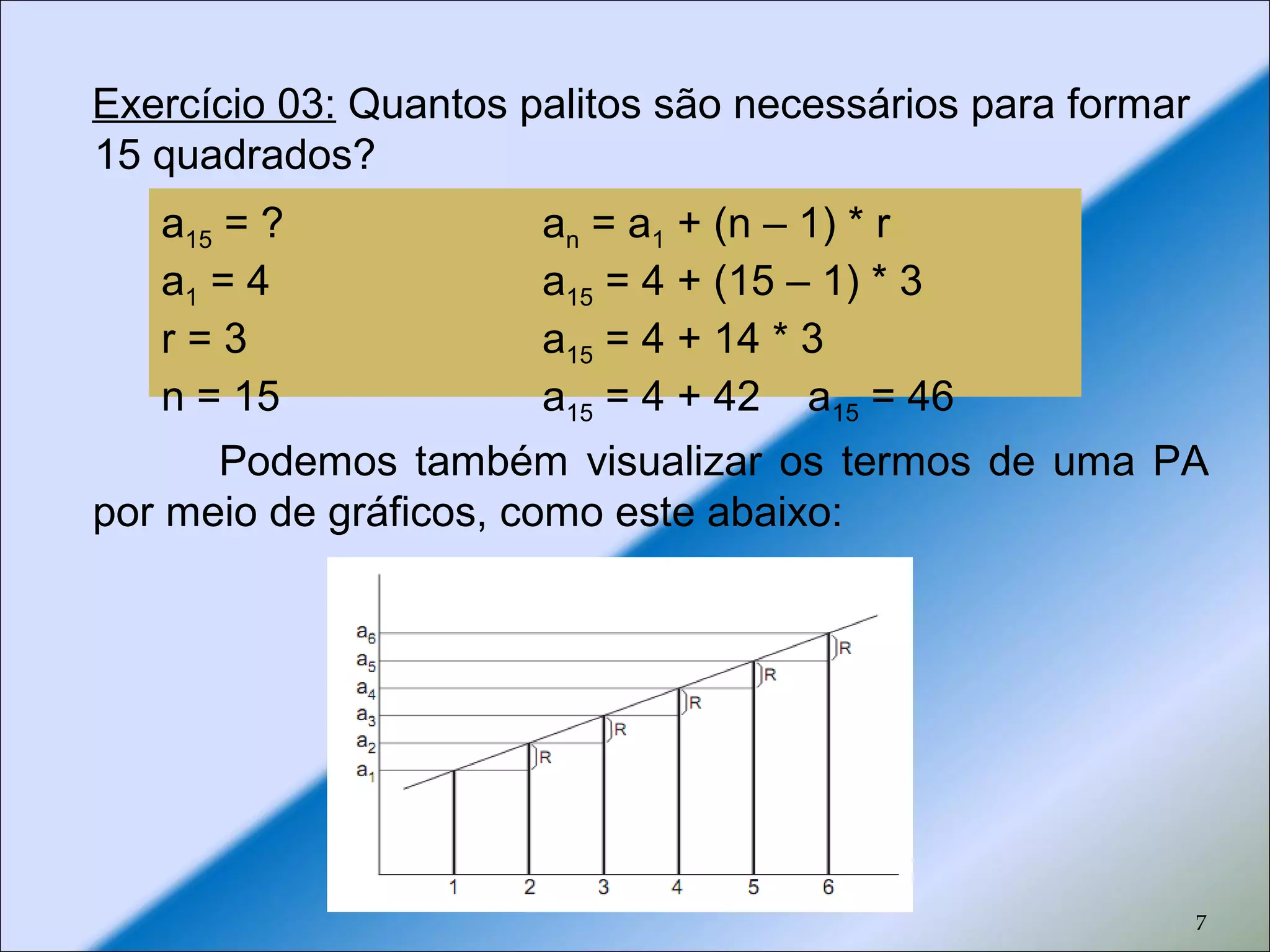
1. Um grupo de amigos se reuniu para um almoço e foram chegando mais pessoas, preenchendo as mesas. Primeiro chegaram 4 pessoas, depois 6 e então 8. 2. Explica como calcular quantas pessoas estavam presentes com base na disposição das mesas e quantas mesas seriam necessárias para 60 pessoas. 3. Apresenta uma fórmula para calcular quantos palitos são necessários para formar um determinado número de quadrados.

1. ARITMÉTICAARITMÉTICA
LUCIENE LIMALUCIENE LIMALUCIENE LIMALUCIENE LIMA

2. 1 – Um grupo de amigos se reuniu para um almoço de
confraternização em um restaurante. Sendo que, a
disposição das mesas irá ser modificada de acordo com
a chegada das pessoas. De primeira chegaram 04
pessoas, depois foram chegando os demais, ficando
assim a distribuição.
2
1ª arrumação 2ª arrumação 3ª arrumação

3. 1ª arrumação a1= n, onde n é o número de lugares
ocupados da mesa
2ª arrumação = a2 ∴
3ª arrumação = a3∴
3
a1 = 4
a2 = 6
a3 = 8
PA (4, 6, 8,...)
PA (a1, a2, a3,...)

4. Quantas pessoas tem nessa Confraternização?
De a2 (segunda arrumação) para a a1 (primeira
arrumação), chegaram 2 pessoas. Essa diferença entre as
arrumações chama-se razão, e podemos representar
assim: a3 – a2 = a2 – a1 = r.
4
+ r - r
PA (a1, a2, a3,..., an-1, an)
a2 = a1 + r
a3 = a2 + r
.
. n – 1 igualdades
.
an = an-1 + r
Fórmula do Termo
Geral da PA
an = a1 + (n – 1) * r

5. Exercício 01: Usando esta arrumação, se foram colocadas
6 mesas e todos os lugares ocupados,
quantas pessoas estavam presente?
5
an = ? an = a1 + (n – 1) * r
n = 6 a6 = 4 + (6 – 1) * 2
r = 2 a6 = 4 + 5 * 2
a1 = 4 a6 = 4 + 10
a6 = 14
Exercício 02:E se comparecerem à confraternização 60
pessoas, quantas mesas serão necessárias?
a60 = ? an = a1 + (n – 1) * r
n = 60 a60 = 4 + (60 – 1) * 2
r = 2 a60 = 4 + 59 * 2
a1 = 4 a60 = 4 + 118 a60= 122

6. 2 – O que você pode observar nas figuras abaixo?
Complete a tabela:
6
Número de quadrados Número de palitos
1 4
Número de quadrados Número de palitos
1 4
2 7
3 10
... ...

7. Exercício 03: Quantos palitos são necessários para formar
15 quadrados?
7
a15 = ? an = a1 + (n – 1) * r
a1 = 4 a15 = 4 + (15 – 1) * 3
r = 3 a15 = 4 + 14 * 3
n = 15 a15 = 4 + 42 a15 = 46
Podemos também visualizar os termos de uma PA
por meio de gráficos, como este abaixo:

8. De modo geral, se estamos no degrau de número
m, devemos subir m – n degraus. A nossa nova fórmula,
que relaciona dois termos quaisquer, é então:
8
am = an + (m – n) * r
Se você está no 6º degrau de uma escada e deseja
chegar ao 10º degrau, quantos degraus deve subir? A
resposta é simples: 04 degraus. Podemos escrever isso
em linguagem matemática: a10 = a6 + 4 * r

9.  PA crescente quando r > 0
Ex: (3, 4, 5, 6, 7)
a2 = a1 + r
4 = 3 + r
4 – 3 = r r = 1
 PA decrescente quando r < 0
Ex: (10, 8, 6,...)
 PA constante ou estacionária quando r = 0
Ex: (5, 5, 5, 5)
9

10. 10
1. Qualquer termo de uma PA, a partir do segundo, é média aritmética
entre o anterior e o seu posterior.
an = an-1 + an + 1
________
2
2. A soma de dois termos eqüidistantes dos extremos é igual à soma
dos extremos.
PA (1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23)
3 + 21 = 1 + 23 = 24
5 + 19 = 1 + 23 = 24
7 + 17 = 1 + 23 = 24
9 + 15 = 1 + 23 = 24
11 +13 = 1 + 23 = 24

11. 11
A soma Sn dos n termos de uma PA é a média aritmética dos
extremos, multiplicada pelo número de termos.
Sn = (a1 + an) * r
________
2

12. 12
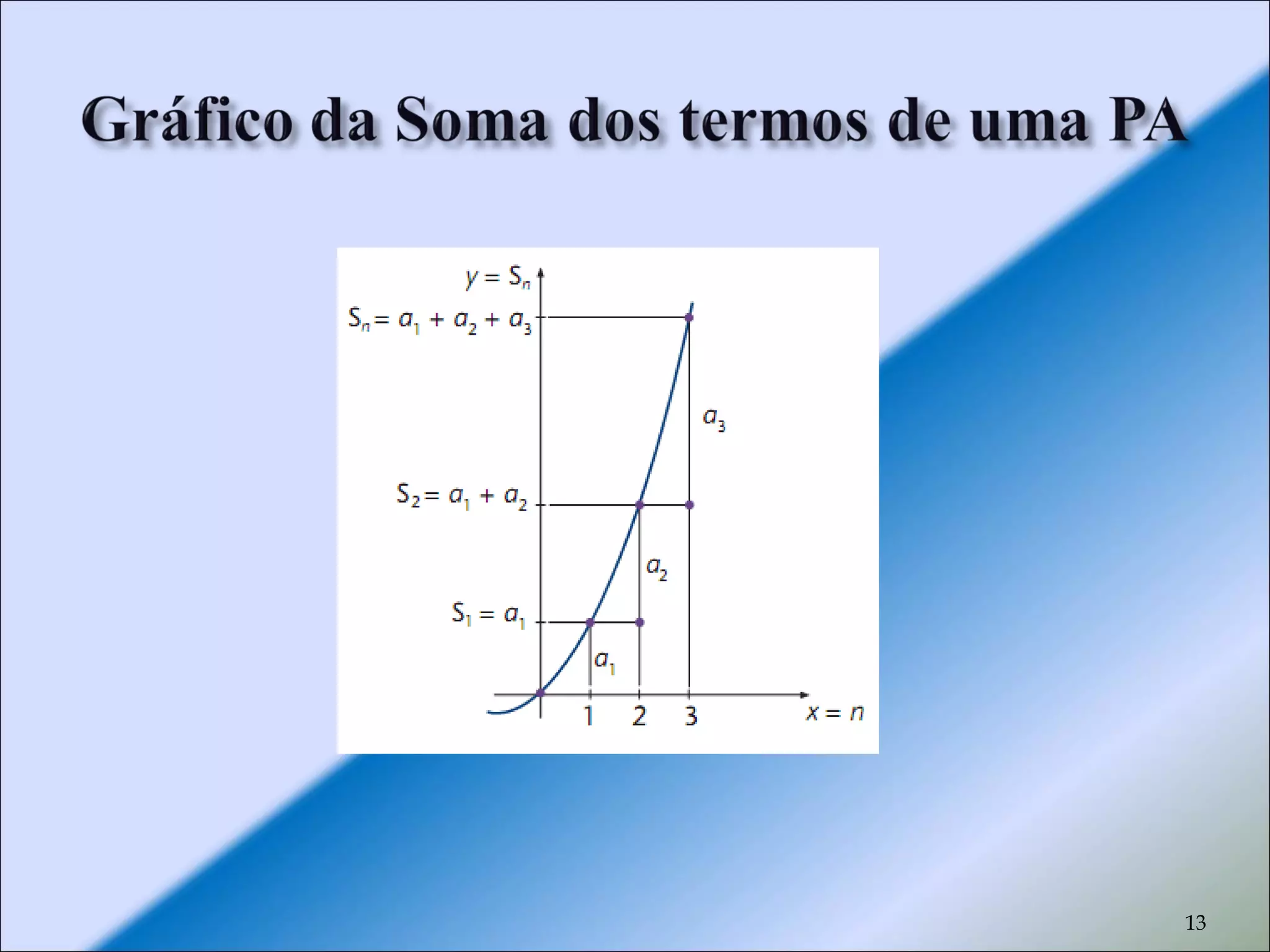
Temos uma função quadrática onde o gráfico é uma
parábola.
Os pontos (n1Sn) são tais que Sn – Sn-1 = an.
As diferenças dos valores assumidos pelas somas
estão em progressão aritmética.
(S1, S2 – S1, S3 – S2, ...., Sn – Sn-1) é uma PA.
Sn = (a1 + an) * n
2
= 1 [ a1 + a1 + (n – 1) * r ] * n
2
= 1 (2 a1 + r n – r) * n
2
Sn = r n2
= ( a1 – r ) * n
2 2

13. 13

14.  YOUSSEF, Antonio Nicolau; FERNANDEZ, Vicente Paz;
SOARES, Elizabeth. Matemática para o 2º grau –
Curso Completo. 2ª edição - Ed. Scipione, 1997.
 DANTE, Luiz Roberto. Matemática Contexto &
Aplicações Ensino Médio. Ed. Àtica.
 GIOVANNI, José Ruy; BONJORNO, José Roberto; JR.,
JoséRuy GIOVANNI. 2º Grau Matemática. Ed. FTD,
1988.
14