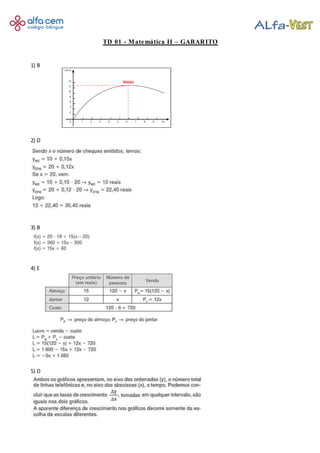
1) Resumo de um teste de Matemática II com 13 questões e gabarito. 2) A questão 10 pede para calcular o valor a ser pago por um cliente que utilizou 74 minutos em uma ligação, considerando que os primeiros 50 minutos são gratuitos. 3) A questão 12 trata de domínio e conjunto imagem de uma função racional.

1. TD 01 - Matemática II – GABARITO
1) B
2) D
3) B
4) E
5) D

2. 6) D
7) E
8) C
9)
a) [-3 6] b) [-1 5]
c) f(f(-1)) = f(2) = 5 d) 2 (o gráfico intercepta o eixo X por duas vezes neste intervalo).
e) {-3, -1, 5} f) f(5) = 2
g) [-2 2] h) g(5) = f(5 + 1) = f(6) = 0.

3. 10)
a) Se o cliente utilizou 74 minutos, então foram ultrapassados (74 – 50) = 24 minutos. Logo o cliente
pagará: 00,76$00,36$00,40$50,1$2400,40$ RRRRR  .
b) Considerando“t”o númerode minutos além dos 50 minutos, a equação que representa esta situação é
R$101,50 = R$40,00 + t x R$1,50.
Resolvendo, temos: min41
5,1
5,61
405,1015,1.5,1405,101  ttt .
Logo, foram utilizados no total (50 + 41) = 91 minutos.
11) D
Preço de venda = 1,60x
Preço de custo = 0,72x
Lucro = 1,60x − 0,72x , ou seja, lucro = 0,88x
Para ter lucro de 1 320 reais, temos:
320 = 0,88x, isto é, x = 1 500 bem-casados
12) Não há restrições no numerador. O denominador apresenta uma raiz. Temos: 303  xx .
Logo,  3/)(  xIRxyD ou  3,)(  IRyD ou   ,3)(yD .
13)
a)
5.3 + 1
5.3 − 1
=
16
14
=
8
7
b)
5𝑥 + 1
5𝑥 − 1
=2
Fazendo a multiplicação cruzada, temos:
5x + 1 = 10x – 2
1 + 2 = 10x – 5x
3 = 5x
X =
3
5
c) 5x – 1 ≠ 0
5x ≠ 1
X ≠
1
5