1. O documento apresenta os conceitos de progressão geométrica e função exponencial, incluindo suas definições e propriedades.
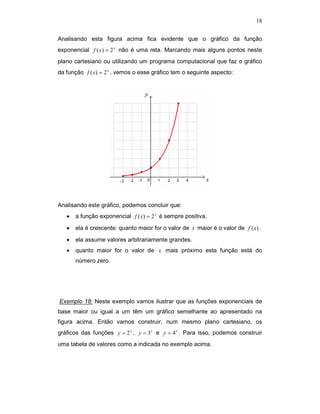
2. Exemplos ilustram como progressões geométricas e funções exponenciais podem ser usadas para modelar situações financeiras, crescimento populacional e outros problemas.
3. O termo geral de uma progressão geométrica é apresentado como uma forma eficiente de determinar qualquer termo da sequência a partir do primeiro termo e da razão.