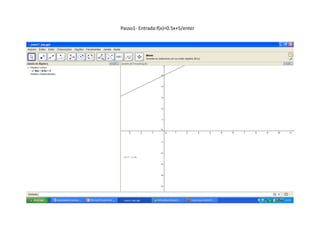
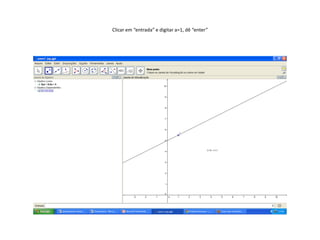
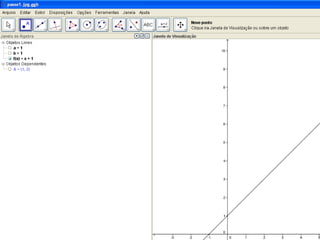
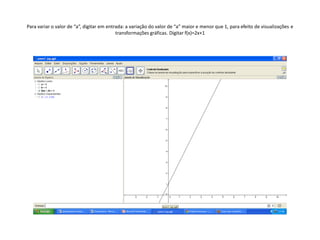
Este documento apresenta um plano de aula sobre funções do 1o grau. Os objetivos são interpretar situações reais em linguagem simbólica e gráfica, construir tabelas e gráficos de funções lineares usando o software Geogebra, e variar os coeficientes angulares e lineares para analisar como isso afeta a inclinação da reta.

1. Planejamento-aula (função 1º grau)
Matemática
1ª série – Ensino Médio

2. Justificativa:
Determinar no aluno, a
correlação entre situações reais
e construções geométricas
artesanais e virtuais.

3. Objetivos gerais e específicos:
#Interpretar uma situação supostamente real e transportá-la para uma linguagem
simbólica e gráfica.
#Construir uma reta a partir de uma tabela que condiciona os valores de y aos
valores de x.
#Utilizar a fórmula que representa a função do 1º grau para encontrar, através de
cálculos de substituição, valores de y que o relacionam respectivamente aos de x.
#Verificar que os coeficientes lineares e angulares assumem valores reais
quaisquer, mudando o comportamento da inclinação da reta, que é a representação
gráfica da função.

4. Etapas e suas estratégias de realização:
Os alunos dispostos em duplas são desafiados a
desvendar uma situação-problema que será exposta
no Projetor digital do Laboratório de Informática
da escola e serão distribuídas apostilas a cada
aluno, na intenção de acompanharem os exercícios
propostos, além de realizarem anotações
necessárias no decorrer da aula.
A situação-problema é a seguinte:
Para a confecção de revistinhas educativas, uma
gráfica cobra um valor de R$ 5,00 referentes ao
custo da capa, contra-capa e da encadernação, mais
um valor de R$ 0,50 para cada página da revista.

5. Pergunta-se:
1)Qual seria a expressão mais apropriada para colocarmos uma
relação de dependência entre duas grandezas, o número de
páginas da revista e o seu custo total? (Sugerir que o número de
páginas seja representado por x e que o custo total seja
representado por f(x).
2)Calcule, na sua apostila, qual seria o custo total a ser gasto, se
a revista tivesse 100 páginas.
3)Calcule, agora, com quantas páginas, o custo total ficaria por
R$900,00 ?
4)Construa uma tabela com os valores correspondentes a x e
f(x) encontrados nas questões 2 e 3.
5)Construa o gráfico correspondente à função formada, com os
pontos listados na tabela.

6. 6)Com o auxílio do professor em relação às ferramentas que o
software Geogebra apresenta, reproduza esse gráfico,
utilizando os mesmos pontos da questão 5.
Instruções para o uso do geogebra no item 6:
No campo Entrada, digitar: f(x)=0.5x+5, depois clicar
enter. (passo 1 na imagem geogebra)
Nesse momento, é importante fazer o aluno comparar a
construção tradicional, (lápis/papel) com a nova realidade
disponível na atualidade, que é a informática.
Ele precisa perceber que há uma valiosa contribuição da
tecnologia na praticidade das construções, mas ele não pode se
desvincular das construções artesanais que são aplicadas
normalmente nas aulas.

7. Passo1- Entrada:f(x)=0.5x+5/enter

8. O próximo item será a confirmação de outros pontos na
mesma reta, ou seja, na mesma função.
7) Introduza mais um ponto que você queira à tabela,
estipulando valores a variável x, para que seja encontrada sua
imagem correspondente. Calcule na sua própria folha de
atividade.
8) Verifique se esse ponto realmente está presente na reta
construída no Geogebra.
Ao confirmar que o ponto realmente está na mesma função, é
necessário que o professor enfatize o fato da reta ser a
representação fiel dos seus cálculos, seja qual for o valor dado
a x, mostrando uma continuidade sequencial.

9. Clicar em “entrada” e digitar a=1, dê “enter”

10. 9)Faça o aluno variar os coeficientes, usando
números reais, para visualizar o
comportamento da reta que representa a função
em cada uma dessas variações.
Instruções para a utilização do Geogebra
(desdobramento dos itens 8 e 9):
i)Clicar em ferramentas/ponto/novo
ponto/deslizar o cursor sobre a reta que
representa a função. Aparecerão vários pontos
pertencentes à reta., até que se conclua sua
previsão do ponto escolhido.(passo2 na
imagem geogebra)

11. iii) Clicar em “entrada” , mantendo a= 1 e
digitar b=1, dê “enter”(passo4)
O gráfico que aparece é referente à função
y=x+1
Observe também que na janela “álgebra” (lado
esquerdo da janela), estão os valores de “a” e
de “b” da função.

13. iv) Para variar o valor de “a”,
digitar em entrada: a variação do
valor de “a” maior e menor que
1, para efeito de visualizações e
transformações gráficas.(passo 5
e 6)

14. Para variar o valor de “a”, digitar em entrada: a variação do valor de “a” maior e menor que 1, para efeito de visualizações e
transformações gráficas. Digitar f(x)=2x+1

15. Para variar o valor de “a”, digitar em entrada: a variação do valor de “a” maior e menor que 1, para efeito de visualizações e
transformações gráficas. Digitar f(x)=-2x+1

16. v) Depois, fazer o mesmo
procedimento feito anteriormente,
dessa vez com o coeficiente linear
b.(passo 7 e 8)

17. Para variar o valor de “b”, digitar em entrada: a variação do valor de “b” maior e menor que 1, para efeito de visualizações e
transformações gráficas. Digitar f(x)=x+2

18. Para variar o valor de “b”, digitar em entrada: a variação do valor de “b” maior e menor que 1, para efeito de visualizações e
transformações gráficas. Digitar f(x)=x-2

19. Avaliação:
O aluno será avaliado em duplas na aula
subsequente às explicações do conteúdos, onde
irá trazer uma situação-problema, expô-la à
turma (um grupo por vez) através do Projetor
Multimídia.
Os colegas da turma deverão encontrar a
expressão algébrica que expressa a lei da
função, em seguida formarão uma tabela que
corresponda à função formada, e depois
reproduzirão seu gráfico no geogebra com os
colegas.

20. Cronograma:
Duas aulas(100 minutos) para
responderem às perguntas da apostila e
realizarem as construções no geogebra.
Duas aulas (100 minutos) para realizarem
a avaliação conforme o item anterior
expõe.