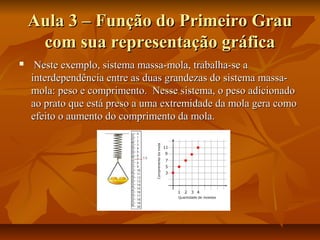
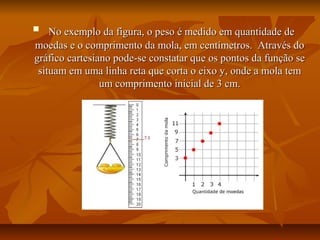
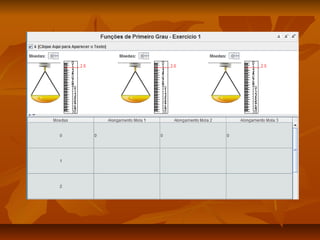
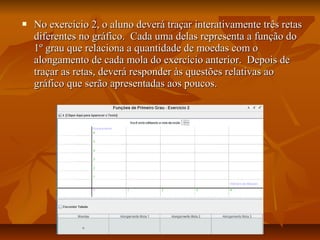
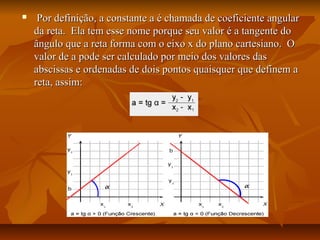
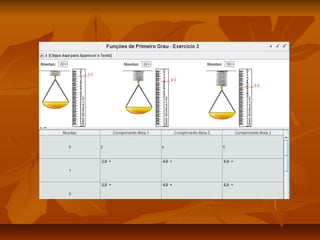
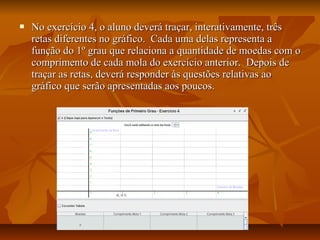
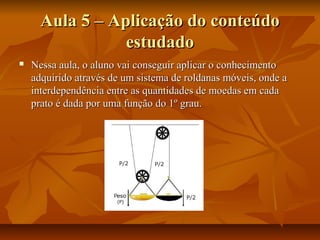
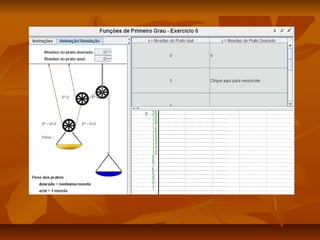
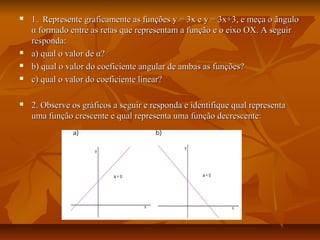
Este documento apresenta um plano de aula para ensinar sobre funções do primeiro grau. A aula introduz o tema através de exemplos do mundo real e vídeos. As aulas subsequentes ensinam sobre representações gráficas, tabelas, analíticas e generalização da função. Atividades práticas no laboratório de informática reforçam os conceitos e uma avaliação final é aplicada.