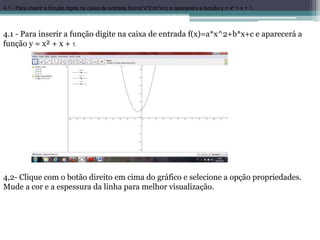
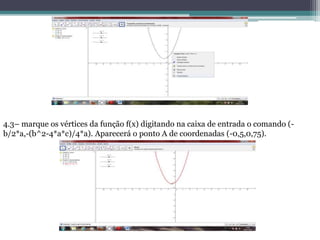
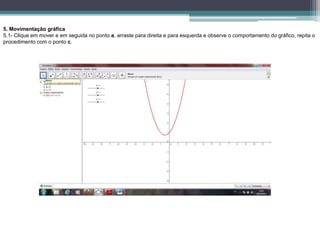
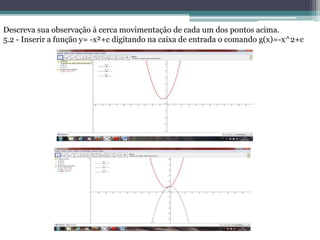
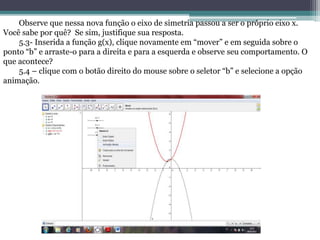
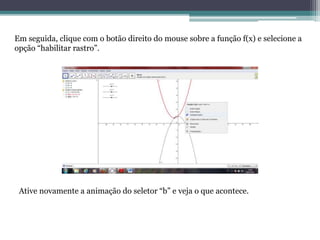
O projeto tem como objetivo avaliar a eficácia do software Geogebra no ensino da função quadrática para alunos do 1º ano do ensino médio. A metodologia envolve a introdução de conceitos matemáticos através de simulações gráficas, promovendo a construção do conhecimento de forma interativa. O Geogebra serve como um recurso didático que facilita a compreensão e investigação matemática, permitindo que os alunos desenvolvam uma aprendizagem ativa e mediada pelo professor.

1. GEOGEBRA COMO RECURSO
DIDÁTICO

2. INFORMATICA EDUCATIVA
Celso Eduardo de Souza Freire

3. PROJETO DE INTERVENÇÃO
FUNÇÃO QUADRÁTICA COM O
USO DO SOFTWARE GEOGEBRA

4. OBJETIVOS:
O presente trabalho tem como objetivo verificar se o
software Geogebra auxiliará no ensino e aprendizagem da
Função Quadrática. Nosso objetivo principal é abordar o
estudo da Função Quadrática com o auxilio desse software de
forma a contribuir para uma melhor compreensão do cotidiano
escolar e mostrando-o como um potente recurso auxiliar da
prática docente.

5. METODOLOGIA
Introduzir o conteúdo de Equação do 2° grau,
turmas de 1° ano do Ensino Médio, com o
auxilio do software GEOGEBRA tendo como
base conduzir os alunos a aprendizagem a partir
da construção gráfica. A partir das observações
desenvolvidas pelos alunos leva-los a perceber
as relações existentes no conteúdo e a dedução
de formulas.

6. •Definição do projeto: Função Quadrática no geogebra e construção de
gráficos.
. Objetivos e metas do projeto: Este projeto tem por objetivo verificar se o
software Geogebra auxiliará no ensino e aprendizagem da Função Quadrática
. Público alvo: Alunos do 1º ano do ensino Médio, faixa etária: 15 anos.
. Quando utilizar: O software será utilizado no momento final do conteúdo,
como mecanismo de sanar dúvidas quanto a construção dos gráficos,
características e fixação do mesmo.
. Local a usar: A atividade ocorrerá no laboratório de informática da escola,
mas os alunos serão orientados a baixar o software e exercitar em casa.
. Custo do projeto:O projeto não terá custo, pois o software é gratuito e de
fácil acesso

7. . Descrição da forma de emprego do projeto:
1. Alunos serão instruídos a “entrar” no software instalado na área
de trabalho do computador.
2. A tela já abre com os eixos “x” e “y”. O aluno deverá clicar com
o botão direito próximos aos eixo e selecionar a opção “malha”. A
malha auxiliara na compreensão de marcação dos pontos.
3. Deixá-los explorar o software por 10 minutos.
4. Representação gráfica Com o programa aberto selecione a
opção “seletor”, clique uma vez na zona gráfica e aparecerá o
intervalo real do coeficiente a. No segundo e terceiro clique
aparecerão os coeficientes b e c. você pode aumentar ou diminuir
o intervalo modificando os valores mínimo e máximo.

9. 4.1 - Para inserir a função digite na caixa de entrada f(x)=a*x^2+b*x+c e aparecerá a função y = x² + x + 1.
4.1 - Para inserir a função digite na caixa de entrada f(x)=a*x^2+b*x+c e aparecerá a
função y = x² + x + 1.
4,2- Clique com o botão direito em cima do gráfico e selecione a opção propriedades.
Mude a cor e a espessura da linha para melhor visualização.

10. 4.3– marque os vértices da função f(x) digitando na caixa de entrada o comando (-
b/2*a,-(b^2-4*a*c)/4*a). Aparecerá o ponto A de coordenadas (-0,5,0,75).

11. 5. Movimentação gráfica
5.1- Clique em mover e em seguida no ponto a, arraste para direita e para esquerda e observe o comportamento do gráfico, repita o
procedimento com o ponto c.

12. Descreva sua observação à cerca movimentação de cada um dos pontos acima.
5.2 - Inserir a função y= -x²+c digitando na caixa de entrada o comando g(x)=-x^2+c

13. Observe que nessa nova função o eixo de simetria passou a ser o próprio eixo x.
Você sabe por quê? Se sim, justifique sua resposta.
5.3- Inserida a função g(x), clique novamente em “mover” e em seguida sobre o
ponto “b” e arraste-o para a direita e para a esquerda e observe seu comportamento. O
que acontece?
5.4 – clique com o botão direito do mouse sobre o seletor “b” e selecione a opção
animação.

14. Em seguida, clique com o botão direito do mouse sobre a função f(x) e selecione a
opção “habilitar rastro”.
Ative novamente a animação do seletor “b” e veja o que acontece.

15. 6. Atividades de Aprendizagem:
6.1 movimentando os pontos a, b e c, representem as funções y = x² - 5x + 6; y = -x²
e y = -2x² + x + 3.
6.2 com relação ao coeficiente a da função o que podemos afirmar segundo o
comportamento do gráfico quando ele for positivo, quando for negativo e quando for
nulo?
6.3 porque é atribuído ao coeficiente c o significado de termo independente?
6.4 – Trace, no mesmo sistema coordenado, os gráficos das seguintes funções
definidas de IR em IR:
y=x² y=x²+2 y=x²-2
a-) determine as coordenadas dos vértices dessas parábolas.
b-) as concavidades das parábolas estão voltadas para cima ou para baixo? Por que?
c-) todas as parábolas que você desenho tem o mesmo eixo de simetria? Se sua
resposta for afirmativa diga qual é esse eixo.
d-) como você pode obter os gráficos de y=x²+2 e y=x²-2 conhecendo o gráfico
y=x²?
6.5 – determine a função quadrática cujo gráfico passa pelos pontos A=(1,8),
B=(0,3) e C=(2,-1).

16. A ESCOLHA DO SOFTWARE

17. O SOFTWARE GEOGEBRA É UM PROGRAMA LIVRE COM
ALTO POTENCIAL DIDÁTICO E PEDAGÓGICO E QUE FACILITA A
INVESTIGAÇÃO DOS ALUNOS, QUE PODEM MOVIMENTAR OS
OBJETOS E ACOMPANHAR AS VARIAÇÕES OCORRIDAS, FAZER
CONJECTURAS E TESTÁ-LAS, ALÉM DE RELACIONAR OS
CONTEÚDOS ALGÉBRICOS E GEOMÉTRICOS.

18. IDENTIFICAÇÃO DO SOFTWARE

19. GEOGEBRA
O GEOGEBRA É UM SOFTWARE CRIADO POR
MARKUS HOHENWARTER DE
RESPONSABILIDADE DA EMPRESA
INTERNATIONAL GEOGEBRA
INSTITUTES

20. O GEOGEBRA É UM SOFTWARE DO TIPO
LIVRE E DE CÓDIGO ABERTO COM UM
PÚBLICO VARIANDO DA ESCOLA PRIMÁRIA
ATÉ O NÍVEL UNIVERSITÁRIO.

21. CONFIGURAÇÕES DO EQUIPAMENTO:
MODELO MÍNIMO DO COMPUTADOR:
WINDOWS 95 E JAVA.
MÉMORIA RAM: 128 MB
ESPAÇO NECESSÁRIO EM DISCO: 4.0 KB
TIPO DE VIDEO: É NECESSÁRIO UM
MONITOR SUPER VGA COM RESOLUÇÃO DE
NO MÍNIMO 800X600 E 256 CORES.
TIPO DE DISCOS: CD, INTERNET, PEN-DRIVE

22. AVALIAÇÃO QUALITATIVA

23. O OBJETIVO É AUXILIAR OS ALUNOS NA
COMPREENSÃO E NA RESOLUÇÃO DE
PROBLEMAS ENVOLVENDO ÁLGEBRA,
GEOMETRIA E CÁLCULO ATRAVÉS DE
VISUALIZAÇÃO E INVESTIGAÇÃO.

24. NÃO HÁ PRÉ-REQUISITOS PARA
UTILIZAÇÃO DO GEOGEBRA. ELE É INDICADO
PARA UTILIZAÇÃO NAS DISCIPLINAS DE
ÁLGEBRA, GEOMETRIA E CÁLCULO.

25. PODEMOS REALIZAR ATIVIDADES TAIS
COMO: CONSTRUÇÕES COM PONTOS,
VETORES, SEGMENTOS, RETAS, SEÇÕES
CÔNICAS, FUNÇÕES, INSERIR EQUAÇÕES E
COORDENADAS DIRETAMENTE.

26. DURANTE A REALIZAÇÃO DE TAIS
ATIVIDADES, OS USUÁRIOS ENCONTRAM
VARIOS NÍVEIS DE DIFICULDADES QUE
VARIAM DE ACORDO COMO SEU DOMÍNIO
DO PROGRAMA.

27. O GEOGEBRA OFERECE FEEDBACK. SEU
RETORNO É SATISFATÓRIO UMA VEZ QUE
PERMITE AO SEU USUÁRIO UMA INTERAÇÃO
COM O OBJETO DE TRABALHO O QUE NA
MAIORIA DAS VEZES NÃO É POSSÍVEL
UTILIZANDO OUTRO RECURSO.

28. O TEMPO PARA A UTILIZAÇÃO É
INDETERMINADO, PORÉM É GERADA UMA GRANDE
ECONOMIA DE TEMPO SE COMPARADO A OUTROS
RECURSOS DIDÁTICOS.
SUAS TELAS E TEXTOS SÃO BEM ADEQUADOS
VISTO QUE OS COMANDOS SÃO BEM FACEIS DE
REALIZAR E A VISUALIZAÇÃO PERMITE UMA
EXCELENTE COMPREENSÃO DO QUE ACONTECE
COM O OBJETO ESTUDADO.

29. O GEOGEBRA É UM SOFTWARE QUE POSSIBILITA
UMA DINAMICIDADE EM QUE SE PODE FAZER
EXPERIMENTAÇÕES POR MEIO DE UM TRABALHO COM
CARACTERÍSTICAS INVESTIGATIVAS. ASSIM, AO INVÉS
DE ALUNOS QUE ESPERAM AS RESPOSTAS E OS
ENCAMINHAMENTOS DO PROFESSOR, TEMOS ALUNOS
QUE LEVANTAM CONJECTURAS E BUSCAM JUSTIFICÁ-
LAS MATEMATICAMENTE. TAL AÇÃO POSSIBILITA QUE
O PROFESSOR ATUE COMO UM MEDIADOR DO
CONHECIMENTO E NÃO COMO UM MERO
TRANSMISSOR.

30. CONCLUSÃO
Através desse projeto foi elaborar atividades
relacionadas ao conteúdo de Equações do 2° grau,
utilizando o software educacional GeoGebra, como
recurso facilitador para a compreensão dos gráficos
e seus movimento.com esse tipo de apoio,os alunos
será auxiliado no processo de abstração,
generalização e permitindo a estes o
desenvolvimento e aprimoramento do pensamento
matemático. É dever do professor buscar aprimorar
suas estratégias de ensino e estar disposto a permitir
que estes se apropriem dos conhecimentos de forma
relevante.

31. REFERENCIAS BIBLIOGRAFICAS:
PONTE, J. P. e Canavarro, A. P. (1997).
Matemática e novas tecnologias. Universidade
Aberta, 95 – 129