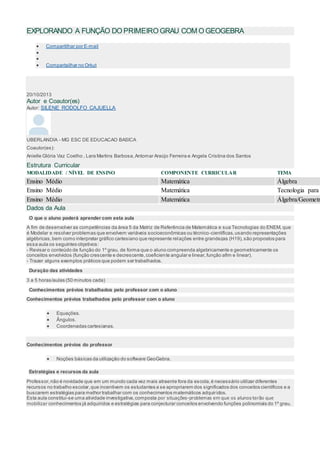
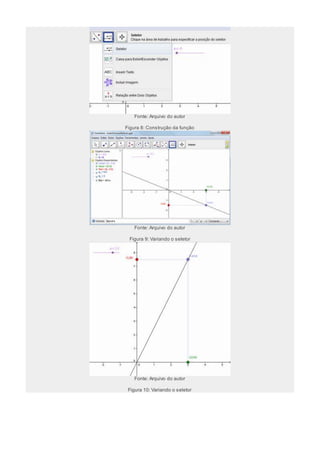
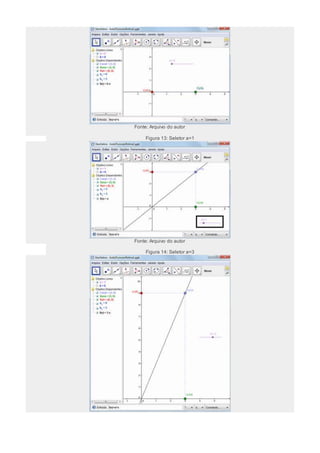
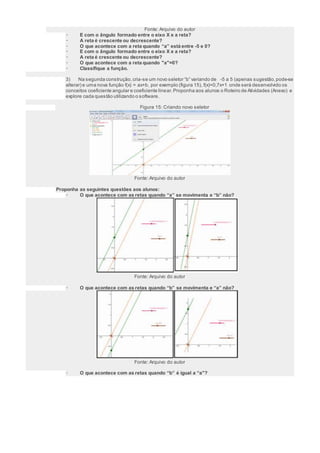
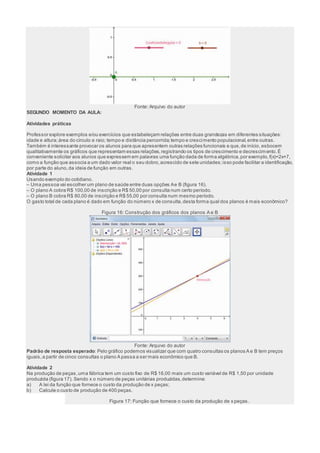
O documento apresenta uma aula sobre a função do primeiro grau utilizando o software GeoGebra. A aula é dividida em dois momentos: no primeiro, os alunos exploram comandos básicos do GeoGebra para construir gráficos de funções; no segundo, realizam atividades práticas com exemplos do mundo real modelados matematicamente. O objetivo é revisar conceitos algébricos e geométricos de função do primeiro grau de forma dinâmica e interativa.

1. EXPLORANDO A FUNÇÃO DO PRIMEIRO GRAU COM O GEOGEBRA
 Compartilhar por E-mail


 Compartailhar no Orkut
20/10/2013
Autor e Coautor(es)
Autor: SILENE RODOLFO CAJUELLA
UBERLANDIA - MG ESC DE EDUCACAO BASICA
Coautor(es):
Anielle Glória Vaz Coelho , Lara Martins Barbosa, Antomar Araújo Ferreira e Angela Cristina dos Santos
Estrutura Curricular
MODALIDADE / NÍVEL DE ENSINO COMPONENTE CURRICULAR TEMA
Ensino Médio Matemática Álgebra
Ensino Médio Matemática Tecnologia para Ensino Médio Matemática Álgebra/Geometria
Dados da Aula
O que o aluno poderá aprender com esta aula
A fim de desenvolver as competências da área 5 da Matriz de Referência de Matemática e sua Tecnologias do ENEM, que
é Modelar e resolver problemas que envolvem variáveis socioeconômicas ou técnico-científicas, usando representações
algébricas, bem como interpretar gráfico cartesiano que represente relações entre grandezas (H19), são propostos para
essa aula os seguintes objetivos:
- Revisar o conteúdo de função do 1º grau, de forma que o aluno compreenda algebricamente e geometricamente os
conceitos envolvidos (função crescente e decrescente, coeficiente angular e linear, função afim e linear).
- Trazer alguns exemplos práticos que podem ser trabalhados.
Duração das atividades
3 a 5 horas/aulas (50 minutos cada)
Conhecimentos prévios trabalhados pelo professor com o aluno
Conhecimentos prévios trabalhados pelo professor com o aluno
 Equações.
 Ângulos.
 Coordenadas cartesianas.
Conhecimentos prévios do professor
 Noções básicas da utilização do software GeoGebra.
Estratégias e recursos da aula
Professor, não é novidade que em um mundo cada vez mais atraente fora da escola, é necessário utilizar diferentes
recursos no trabalho escolar, que incentivem os estudantes a se apropriarem dos significados dos conceitos científicos e a
buscarem estratégias para melhor trabalhar com os conhecimentos matemáticos adquir idos.
Esta aula constitui-se uma atividade investigativa, composta por situações-problemas em que os alunos terão que
mobilizar conhecimentos já adquiridos e estratégias para conjecturar conceitos envolvendo funções polinomiais do 1º grau.

2. Sugere-se, ao final, uma proposta de roteiro para que os alunos respondam no decorrer da execução das
atividades propostas.
Professor, para o desenvolvimento das atividades propostas nessa aula utiliza-se o software GeoGebra para auxiliar a
visualização do plano cartesiano e compreensão de conceitos geométricos. Além disso, deve-se dispor de um projetor
multimídia conectado ao computador com o referido software citado.
Vale lembrar que o software GeoGebra é um programa gratuito e o seu download está disponível em:
<http://www.baixaki.com.br/download/geogebra.htm> (Acesso em 05 out. 2013). Também é possível utilizar este software
online, ou seja, sem realizar sua instalação. Para isso, acesse o
link http://www.geogebra.org/webstart/geogebra.html(Acesso em 05 out 2013).
Comentário: Caso seja possível, aconselha-se que a aula seja desenvolvida em um laboratório de informática com um
computador por aluno ou em dupla para possibilitar a interação e acompanhamento das atividades pelos alunos.
O software GeoGebra - Apresentação
Segundo Humberto José Bortolossi (s.d.), o GeoGebra, criado por Markus Hohenwarter, é um software gratuito de
matemática dinâmica desenvolvido para o ensino e aprendizagem da matemática nos vários níveis de ensino (do básico ao
universitário). O GeoGebra reúne recursos de geometria, álgebra, tabelas, gráficos, probabilidade, estatística e cálculos
simbólicos em um único ambiente. Assim, o GeoGebra tem a vantagem didática de apresentar, ao mesmo tempo,
representações diferentes de um mesmo objeto que interagem entre si. Além dos aspectos didáticos, o GeoGebra é uma
excelente ferramenta para se criar ilustrações profissionais para serem usadas em outros programas, como no Microsoft
Word, no Open Office, no LaTeX, entre outros. Escrito em JAVA e disponível em português, o GeoGebra é multiplataforma
e, portanto, ele pode ser instalado em computadores com Windows, Linux ou Mac OS. (Disponível no
site http://www.geogebra.im-uff.mat.br/. Acesso em 08 out. 2013)
A utilização de softwares de geometria dinâmica pode favorecer a verificação de hipóteses e conjecturas levantadas pelos
alunos de maneira mais dinâmica, permitindo-lhes escolher seus próprios caminhos, interagir com outros espaços e seguir
o seu próprio ritmo de aprendizagem, o que nem sempre é possibilitado na escola.
Sobre softwares de geometria dinâmica, Baldin (2003), defende que estes possuem qualidades de visualização e de
interatividade para explorar propriedades e podem ser utilizados para auxiliar a construção dos conhecimentos, assim como
podem auxiliar na modelagem de problemas e nas simulações. Esses programas permitem manipulação fácil e
especulação de conceitos pelo próprio aluno, o que aumenta seu prazer em interagir com a tecnologia para construir
conhecimentos matemáticos.
Ainda sobre esta questão, as orientações dos PCN (BRASIL, 1998), afirmam que o uso de computadores pode trazer
significativas contribuições para repensar o processo de ens ino e aprendizagem de matemática, pois “relativiza a
importância do cálculo mecânico e da simples manipulação simbólica, uma vez que por meio de instrumentos
esses cálculos podem ser realizados de modo mais rápido e eficiente; possibilita o desenvolvimento, nos alunos,
de um crescente interesse pela realização de projetos e atividades de investigação e exploração como parte
fundamental de sua aprendizagem; permite que os alunos construam uma visão mais completa da verdadeira
natureza da atividade matemática e desenvolvam atitudes positivas diante de seu estudo” (BRASIL, 1998, pp.43-4).
PRIMEIRO MOMENTO DA AULA:
O software GeoGebra: fazendo construções simples
Ao instalar o GeoGebra, um atalho será criado na sua área de trabalho. Para começar a utilizá -lo, basta dar um duplo clique
sobre o atalho.
Após abrir o programa, permita que os alunos se familiarizem com a estrutura do software, em seguida, solicite que os
alunos explorem comandos básicos do software, conforme as ilustrações a seguir (Figuras 1, 2, 3, 4 e 5):
Figura 1: Tela inicial do GeoGebra
Fonte: Disponível em: <http://www.geogebra.org/help/docupt_PT.pdf>. Acesso em 05 out 2013.
Figura 2: Ícones da Barra de Ferramentas

3. Fonte: Disponível em: <http://www.geogebra.org/help/docupt_PT.pdf>. Acesso em 05 out 2013.
Figura 3: Ícones da Barra de Ferramentas
Fonte: Disponível em: <http://www.geogebra.org/help/docupt_PT.pdf>. Acesso em 05 out 2013.
Figura 4: Ícones da Barra de Ferramentas
Fonte: Disponível em: <http://www.geogebra.org/help/docupt_PT.pdf>. Acesso em 05 out 2013.
Figura 5: Ícones da Barra de Ferramentas

4. Fonte: Disponível em: <http://www.geogebra.org/help/docupt_PT.pdf>. Acesso em 05 out 2013.
Caso deseje explorar todos os comandos, solicite que os alunos acessem o Manual Oficial do programa da Versão 3.2. O
manual está disponível em: <http://www.geogebra.org/help/docupt_PT.pdf>. Acesso em 05 out 2013.
1) Na primeira construção solicite a criação de um canal (x,y) de tal forma que o aluno
compreenda a relação existente entre as abscissas e as coordenadas (figura 6).
Figura 6: Construção das coordenadas no GeoGebra
Fonte: Arquivo do autor
Comentário: Nomeie as coordenadas de maneira não convencional (Como exemplo, usaremos: Xuxa, Yuri) relacionando-as
(Canal). Desta forma, o aluno des prenderá de alguns conceitos form ais impostos a eles , tais como a letra “x” es tará s empre
relacionada ao eixo das abs cis sas e a letra “y” ao eixo das coordenadas.
1) Cria-se (figura 7) um seletor "a" variando de -5 a 5 (figuras 9, 10 e 11). Logo após, no campo
“Entrada” cria-se a função f(x) = ax, de tal forma que o aluno perceba a relação entre Xuxa (x) e
Yuri (y) (figura 8).
Figura 7: Construção do seletor

5. Fonte: Arquivo do autor
Figura 8: Construção da função
Fonte: Arquivo do autor
Figura 9: Variando o seletor
Fonte: Arquivo do autor
Figura 10: Variando o seletor

6. Fonte: Arquivo do autor
Figura 11: Variando o seletor
Fonte: Arquivo do autor
2) Para o desenvolvimento dos conceitos de função crescente, decrescente e constante
proponha as seguintes questões aos alunos:
· O que acontece com a reta quando "a" está entre 0 e 5?
Comentário: Mostre aos alunos, através do software, a variação do seletor (figuras 12, 13 e 14). Segue alguns exemplos:
Figura 12: Seletor a=0

7. Fonte: Arquivo do autor
Figura 13: Seletor a=1
Fonte: Arquivo do autor
Figura 14: Seletor a=3

8. Fonte: Arquivo do autor
· E com o ângulo formado entre o eixo X e a reta?
· A reta é crescente ou decrescente?
· O que acontece com a reta quando “a” está entre -5 e 0?
· E com o ângulo formado entre o eixo X e a reta?
· A reta é crescente ou decrescente?
· O que acontece com a reta quando "a"=0?
· Classifique a função.
3) Na segunda construção, cria-s e um novo s eletor “b” variando de -5 a 5 (apenas sugestão, pode-se
alterar) e uma nova função f(x) = ax+b, por exemplo (figura 15), f(x)=0,7x+1 onde será desenvolvido os
conceitos coeficiente angular e coeficiente linear. Proponha aos alunos o Roteiro de Atividades (Anexo) e
explore cada questão utilizando o software.
Figura 15: Criando novo seletor
Fonte: Arquivo do autor
Proponha as seguintes questões aos alunos:
· O que acontece com as retas quando “a” se movimenta e “b” não?
Fonte: Arquivo do autor
· O que acontece com as retas quando “b” se movimenta e “a” não?
Fonte: Arquivo do autor
· O que acontece com as retas quando “b” é igual a “a"?

9. Fonte: Arquivo do autor
SEGUNDO MOMENTO DA AULA:
Atividades práticas
Professor explore exemplos e/ou exercícios que estabeleçam relações entre duas grandezas em diferentes situações:
idade e altura; área do círculo e raio; tempo e distância percorrida; tempo e crescimento populacional, entre outras.
Também é interessante provocar os alunos para que apresentem outras relações funcionais e que, de início, esbocem
qualitativamente os gráficos que representam essas relações, registrando os tipos de crescimento e decrescimento. É
conveniente solicitar aos alunos que expressem em palavras uma função dada de forma algébrica, por exemplo, f(x)=2x+7,
como a função que associa a um dado valor real o seu dobro, acrescido de sete unidades; isso pode facilitar a identificação,
por parte do aluno, da ideia de função em outras.
Atividade 1
Usando exemplo do cotidiano.
– Uma pessoa vai escolher um plano de saúde entre duas opções A e B (figura 16).
– O plano A cobra R$ 100,00 de inscrição e R$ 50,00 por consulta num certo período.
– O plano B cobra R$ 80,00 de inscrição e R$ 55,00 por consulta num mesmo período.
O gasto total de cada plano é dado em função do número x de consulta, desta forma qual dos planos é mais econômico?
Figura 16: Construção dos gráficos dos planos A e B
Fonte: Arquivo do autor
Padrão de resposta esperado: Pelo gráfico podemos visualizar que com quatro consultas os planos A e B tem preços
iguais, a partir de cinco consultas o plano A passa a ser mais econômico que B.
Atividade 2
Na produção de peças, uma fábrica tem um custo fixo de R$ 16,00 mais um custo variável de R$ 1,50 por unidade
produzida (figura 17). Sendo x o número de peças unitárias produzidas, determine:
a) A lei da função que fornece o custo da produção de x peças;
b) Calcule o custo de produção de 400 peças.
Figura 17: Função que fornece o custo da produção de x peças.

10. Fonte: Arquivo do autor
Padrão de respostas esperadas:
a) f(x) = 1,5x + 16
b) f(x) = 1,5x + 16
f(400) = 1,5*400 + 16
f(400) = 600 + 16
f(400) = 616
Comentário: O custo para produzir 400 peças será de R$ 616,00.
BALDIN, Yuriko Yamamoto. Utilizações diferenciadas de recursos computacionais no ensino de matemática (CAS, DGS e
Calculadoras Gráficas). In: CARVALHO, Luiz M.; GUIMARÃES, Luiz C. (Org.). História e tecnologia no ensino de
Matemática. Rio de Janeiro: IME-UERJ, 2003. p. 27-36. v. 1.
BRASIL. Ministério da Educação. Secretaria de Ensino Fundamental. Referenciais para a formação de professores.
Brasília: MEC/SEF, Brasília, 1997.
______. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais: Matemática. Brasília: MEC/SEF,
Brasília, 1998.
ORIENTAÇÕES CURRICULARES PARA O ENSINO MÉDIO. Ciências da Natureza Matemática e suas Tecnologias.
Disponível em: <http://portal.mec.gov.br/seb/arquivos/pdf/book_volume_02_internet.pdf>. Acesso em 12 ago 2013.
ROTEIRO DE ATIVIDADES
· O que acontece com a reta quando a está entre 0 e 5? E o ângulo formado entre o eixo X e a reta? A reta é
crescente ou decrescente?
___________________________________________________________________________________________________
___________________________________________________________________________________________________
________________________________
· O que acontece com a reta quando a está entre -5 e 0? E o ângulo formado entre o eixo X e a reta? A reta é
crescente ou decrescente?
___________________________________________________________________________________________________
___________________________________________________________________________________________________
________________________________
· O que acontece com a reta quando a=0? Classifique a função.
___________________________________________________________________________________________________
___________________________________________________________________________________________________
________________________________
· O que acontece com as retas quando a se movimenta e b não?
___________________________________________________________________________________________________
___________________________________________________________________________________________________
________________________________
· O que acontece com as retas quando b se movimenta e a não?

11. ___________________________________________________________________________________________________
___________________________________________________________________________________________________
_________________________________
Recursos Complementares
Como recurso complementar o professor pode consultar:
1. SOARES, L.H.; Contribuições do uso do GeoGebra no estudo de funções. Apresentação disponível em:
<http://www4.pucsp.br/geogebrala/submissao/pdfs/20LUISHAVELANGE_APRES.pdf> Acesso em 12 ago 2013.
2. FARIAS, C. B. L; ALVES, E. L.. O ensino da função afim com o auxílio do software geogebra. XI Encontro Nacional
de Educação Matemática. Disponível em: <http://sbem.bruc.com.br/XIENEM/pdf/1905_1672_ID.pdf> Acesso em 12 ago
2013.
3. O Site “Dia a dia educação” abordando exemplos práticos. Disponível
em:< http://www.matematica.seed.pr.gov.br/modules/conteudo/conteudo.php?conteudo=130> Acesso em 12 ago 2013.
4. Um vídeo (Função a fim no GeoGebra) disponível em: <http://www.youtube.com/watch?v=NEc1_nEQKDM>. Acesso
em 12 ago 2013.
5. ORIENTAÇÕES CURRICULARES PARA O ENSINO MÉDIO. Ciências da Natureza, Matemática e suas Tecnologias.
Disponível em: <http://portal.mec.gov.br/seb/arquivos/pdf/book_volume_02_internet.pdf>. Acesso em 12 ago 2013.
Avaliação
Avalie o aluno durante a aula investigativa e através do roteiro de atividade (Anexo). A avaliação também poderá ser feita a
partir de uma lista de exercícios práticos propostos no decorrer da aula. Além di sso, as construções dos alunos podem ser
salvas para serem avaliadas pelo professor, posteriormente.
Opinião de quem acessou
Cinco estrelas 2 classificações
 Cinco estrelas2/2 - 100%
 Quatro estrelas0/2 - 0%
 Três estrelas0/2 - 0%
 Duas estrelas0/2 - 0%
 Uma estrela0/2 - 0%
Denuncie opiniões ou materiais indevidos!
Opiniões
 Telma, Colégio Estadual Hélio Rangel , Rio de Janeiro - disse:
telmateacher@ig.com.br
23/04/2014
Cinco estrelas
Parabéns, professor, por utilizar outros meios didáticos, que com certeza levarão os alunos a uma apendizagem
mais significtiva e prazerosa. Gostei muito da aula e estarei aproveitando-a em minhas aulas.
 JESSE OLIVEIRA NOLASCO, ESC ANTONIO OLIVEIRA DANTAS , Acre - disse:
jessenolasco@gmail.com
11/02/2014
Cinco estrelas

12. O uso das Tics onde o ambiente escolar possibilitar ate 2 alunos por maquina, muito contribuirá para a
aprendizagem do aluno, neste caso o trabalho acima é um excelente material por ser muito bem elaborado,
parabéns, inclusive vou usa-lo este ano.
http://portaldoprofessor.mec.gov.br/fichaTecnicaAula.html?aula=52998