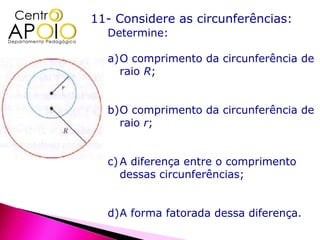
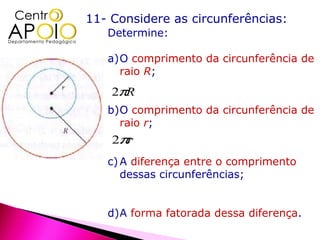
O documento aborda a fatoração de polinômios e expressões algébricas, apresentando exemplos de como encontrar fatores comuns e fatorar binômios. Além disso, inclui questões sobre a resolução de equações e a comparação de áreas de figuras geométricas. O conteúdo é direcionado a estudantes do ensino fundamental, com foco em práticas de matemática.