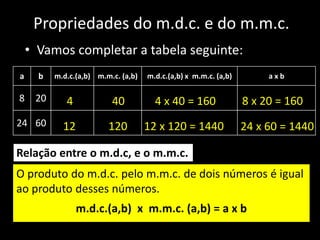
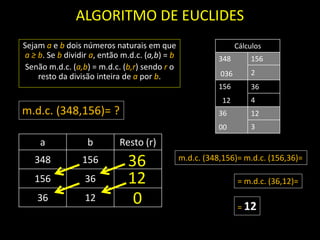
O documento descreve propriedades e algoritmos para calcular o máximo divisor comum (m.d.c.) e mínimo múltiplo comum (m.m.c.) de números. Apresenta a relação entre m.d.c. e m.m.c., onde o produto deles é igual ao produto dos números. Também explica o Algoritmo de Euclides para calcular m.d.c. de forma iterativa, subtraindo o resto das divisões sucessivas.

2. Propriedades do m.d.c. e do m.m.c.
• Vamos completar a tabela seguinte:
a b m.d.c.(a,b) m.m.c. (a,b) m.d.c.(a,b) x m.m.c. (a,b) a x b
8 20
24 60
4 40 4 x 40 = 160 8 x 20 = 160
12 120 12 x 120 = 1440 24 x 60 = 1440
Relação entre o m.d.c, e o m.m.c.
O produto do m.d.c. pelo m.m.c. de dois números é igual
ao produto desses números.
m.d.c.(a,b) x m.m.c. (a,b) = a x b

3. Propriedades do m.d.c. e do m.m.c.
Considera os números: 24 e 60
• m.d.c. (24,60) =
Relação entre o m.d.c, e o m.m.c.
Dividindo dois números pelo seu m.d.c.
obtêm-se dois números primos entre si
12
24 : 12 = 2 60 : 12 = 5
m.d.c. (2,5) = 1 (2 e 5 são números primos entre si)

4. ALGORITMO DE EUCLIDES
Método simples para determinar o m.d.c. de dois
números naturais
Este método foi
apresentado no Livro VII dos
Elementos (+ ou – 300 a. C.)
Este algoritmo é um dos
mais antigos ainda utilizados Euclides 360 a 295 a. C.

5. ALGORITMO DE EUCLIDES
Método simples para determinar o m.d.c. de dois
números naturais
Sejam a e b dois números naturais em que a ≥
b. Se b dividir a, então m.d.c. (a,b) = b
Senão m.d.c. (a,b) = m.d.c. (b,r) sendo r o resto
da divisão inteira de a por b.

6. ALGORITMO DE EUCLIDES
Sejam a e b dois números naturais em que a ≥ b. Se b dividir a,
então m.d.c. (a,b) = b
Senão m.d.c. (a,b) = m.d.c. (b,r) sendo r o resto da divisão inteira
de a por b.
a b Resto (r)
2250 450
Aplicação do Algoritmo de Euclides
Cálculos
2250
000
450
5
m.d.c. (2250,450)= ?
o
m.d.c. (2250,450)= 450

7. ALGORITMO DE EUCLIDES
Sejam a e b dois números naturais em que
a ≥ b. Se b dividir a, então m.d.c. (a,b) = b
Senão m.d.c. (a,b) = m.d.c. (b,r) sendo r o
resto da divisão inteira de a por b.
a b Resto (r)
348 156
156 36
36 12
Cálculos
348
036
156
2
156
12
36
4
36
00
12
3
m.d.c. (348,156)= ?
36 m.d.c. (348,156)= m.d.c. (156,36)=
12
0
= m.d.c. (36,12)=
= 12