O documento apresenta uma revisão de operações fundamentais, incluindo sinais, ordem de cálculo, adição, subtração, multiplicação, divisão, frações, números decimais, potência, radiciação. As principais propriedades e regras de cada operação são descritas de forma concisa.
![REVISÃO: OPERAÇÕES FUNDAMENTAIS
Estudo dos Sinais
)
(
)
(
)
( +
=
+
⋅
+
)
(
)
(
)
( +
=
−
⋅
−
)
(
)
(
)
( −
=
−
⋅
+
)
(
)
(
)
( −
=
+
⋅
−
Ordem de Cálculo
Primeiro são resolvidas as operações que estiverem dentro de:
PARÊNTESES ( ) → COLCHETES [ ] → CHAVES { }
Antes de serem efetuadas adições e subtrações, são resolvidas:
DIVISÕES E MULTIPLICAÇÕES
Adição
Soma
Parcelas
c
b
a
↓
↓
↓
=
+
Propriedades
Comutativa → a
b
b
a +
=
+ 8
3
5
5
3 =
+
=
+
⇒
Associativa → )
c
b
(
a
c
)
b
a
( +
+
=
+
+ 10
)
5
2
(
3
5
)
2
3
( =
+
+
=
+
+
⇒
Elemento Neutro (0) → a
0
a =
+ 3
0
3 =
+
⇒
→ Subtração é a Adição de parcelas negativas
O resultado tem o sinal da maior parcela:
13
15
3
20
5
10
5
5
10
5
5
10 −
=
+
−
−
+
−
−
=
+
−
+
=
−
+
Subtração
Soma
Parcelas
c
b
a
)
b
(
a
↓
↓
↓
=
−
=
−
+
Multiplicação
Produtos
Fatores
c
b
a
↓
↓
↓
=
⋅
Multiplicação é a Adição de parcelas iguais: 15
5
5
5
5
3
5
fator
o
vezes
3
=
+
+
=
⋅ 4
3
4
2
1
Propriedades
Comutativa → a
b
b
a ⋅
=
⋅ 15
3
5
5
3 =
⋅
=
⋅
⇒
Associativa → )
c
b
(
a
c
)
b
a
( ⋅
⋅
=
⋅
⋅ 30
)
5
2
(
3
5
)
2
3
( =
⋅
⋅
=
⋅
⋅
⇒
Elemento Neutro (1) → a
1
a =
⋅ 3
1
3 =
⋅
⇒
Distributiva → c
a
b
a
)
c
b
(
a ⋅
+
⋅
=
+
⋅ 16
5
2
3
2
)
5
3
(
2 =
⋅
+
⋅
=
+
⋅
⇒
a
c
a
b
a
)
c
b
( ⋅
+
⋅
=
⋅
+ 9
)
3
(
2
)
3
(
1
)
3
(
)
2
1
( −
=
−
⋅
+
−
⋅
=
−
⋅
+
⇒
Divisão
c
b
a
=
Numerador = Denominador × Quociente + Resto
Lembre-se: Não existe divisão por zero → b ≠ 0 !
1](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/75/Mapa-mental-todas-as-materias-1-2048.jpg)






![PORCENTAGEM
Porcentagem ou percentagem é uma razão centesimal representada pelo símbolo (%) e indica a
divisão de um número por cem.
Exemplo: Um carro popular valia em 1994 8 mil reais. Em 2006, um carro similar custa o
equivalente a 13 mil reais. Qual o aumento de preço percentual ao longo do período?
O resultado pode ser obtido através de uma regra de três simples:
Ano Valor do Carro (R$) Valor correspondente em (%)
1994 8000 100
2006 13000 x
↑ ↑
%
5
,
62
1
x
8
1300
x
8000
13000
100
x
=
⇒
=
⇒
= O aumento percentual de preço no período foi de 62,7%
SISTEMA INTERNACIONAL DE UNIDADES DE MEDIDA
U
Un
ni
id
da
ad
de
es
s F
Fu
un
nd
da
am
me
en
nt
ta
ai
is
s d
do
o S
SI
I
N
No
om
me
e S
Sí
ím
mb
bo
ol
lo
o
C
Co
om
mp
pr
ri
im
me
en
nt
to
o m
me
et
tr
ro
o ]
m
[
M
Ma
as
ss
sa
a q
qu
ui
il
lo
og
gr
ra
am
ma
a ]
kg
[
T
Te
em
mp
po
o s
se
eg
gu
un
nd
do
os
s ]
s
[
I
In
nt
te
en
ns
si
id
da
ad
de
e d
de
e C
Co
or
rr
re
en
nt
te
e E
El
lé
ét
tr
ri
ic
ca
aaa a
am
mp
pè
èr
re
e ]
A
[
T
Te
em
mp
pe
er
ra
at
tu
ur
ra
a T
Te
er
rm
mo
od
di
in
nâ
âm
mi
ic
ca
a K
Ke
el
lv
vi
in
n ]
K
[
I
In
nt
te
en
ns
si
id
da
ad
de
e L
Lu
um
mi
in
no
os
sa
a c
ca
an
nd
de
el
la
a ]
cd
[
A
Al
lg
gu
un
ns
s P
Pr
re
ef
fi
ix
xo
os
s d
do
o S
SI
I
F
Fa
at
to
or
r P
Pr
re
ef
fi
ix
xo
o S
Sí
ím
mb
bo
ol
lo
o
1
10− d
de
ec
ci
i d
2
10− c
ce
en
nt
ti
i c
3
10− m
mi
il
li
i m
6
10− m
mi
ic
cr
ro
o μ
9
10− n
na
an
no
o n
3
10 k
ki
il
lo
o k
6
10 m
me
eg
ga
a M
Exemplos de conversão de unidades
Sistema Internacional de Medidas (SI) Conjunto de unidades utilizada para medir e comparar
todas as espécies de grandezas, possibilitando ainda a operação com seus múltiplos e submúltiplos.
Conversão de m
30 em m
μ , mm, cm, dm e km
m
μ mm cm dm km
Conversãoa 3
2
1
m
6
6
m
10
10
30
μ
−
×
× 3
2
1
mm
3
3
m
10
10
30 −
×
× 3
2
1
cm
2
2
m
10
10
30 −
×
× 3
2
1
dm
1
1
m
10
10
30 −
×
× 3
2
1
km
3
3
m
10
10
30 ×
× −
Valor m
10
.
3 7
μ mm
000
.
30 cm
000
.
3 dm
300 km
03
,
0
Outras Grandezas
Massa Tempo Velocidade Área Volume
Valor original kg
5 h
3 h
/
km
60 2
cm
120 3
7
mm
10
Converter para ]
g
[ ]
s
[ ]
s
/
m
[ 2
]
m
[ 3
]
m
[
Conversão g
10
5 3
× s
3600
3×
s
3600
m
10
60 3
× 2
2
)
m
10
(
120 −
× 3
3
7
)
m
10
(
10 −
×
Valor convertidovv g
000
.
5 s
800
.
10 s
/
m
67
,
16 2
m
012
,
0 3
m
01
,
0
8](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-8-320.jpg)


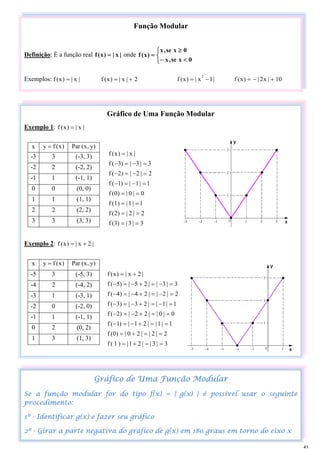
![Sistema Cartesiano Ortogonal
O sistema cartesiano pode ser utilizado para representar os pares ordenados de uma relação. Este sistema
divide o plano em quatro quadrantes:
Gráfico de Uma Relação
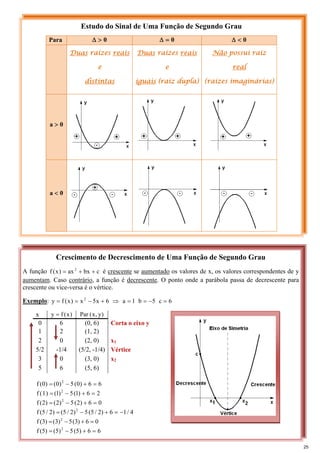
Crescimento e Decrescimento de Uma Função
x aumenta e y aumenta: a função é crescente ⇒ [0, 2] e [7, 10]
x aumenta e y diminui: a função é decrescente ⇒ [2, 7]
Raiz ou Zero da Função
São os pontos onde o gráfico corta o eixo x. São chamados raízes ou zero da
função, este último pelo fato de suas ordenadas serem nulas
São raízes ou zeros da função ⇒ 0, 4 e 10
Sinal de Uma Função
Se o gráfico estiver acima do eixo x: a função é positiva ⇒ ]0, 4[
Se o gráfico estiver abaixo do eixo x: a função é negativa ⇒ ]4, 10[
⇒ O ponto de interseção dos eixos é a origem do sistema
⇒ O ponto (x, y) são números reais e representam as ordenadas do ponto
⇒ Onde x é a abscissa e y a ordenada desse ponto
16](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-16-320.jpg)














![Gráfico de Uma Função Logarítmica
Outros Exemplos
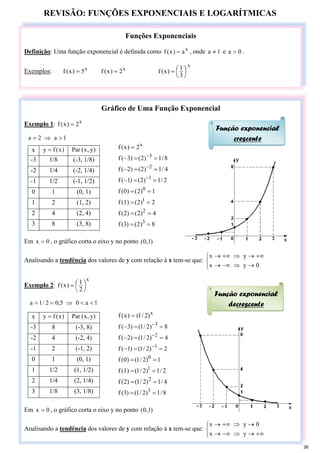
Exemplo 1: Faça o gráfico da função )
x
1
(
log
)
x
(
f 5
+
=
Em 0
y = , o gráfico corta o eixo x no ponto )
0
,
0
( :
0
x
x
1
1
x
1
5
)
x
1
(
log
0
)
x
1
(
log
)
x
(
f
y 0
5
5
=
⇒
+
=
⇒
+
=
⇒
+
=
⇒
+
=
=
Na função dada, o logaritmando é diferente de x ( x
b ≠ ). Para avaliar os valores que x pode assumir na
função, utiliza-se a condição de que b é positivo ( 0
b > ). Assim: 1
x
0
x
1 −
>
⇒
>
+
Desta forma, tem-se que x pode assumir valores dentro do intervalo: [
,
1
] ∞
+
−
Analisando a tendência dos valores de y em relação à x tem-se que:
⎩
⎨
⎧
−∞
→
⇒
−
→
+∞
→
⇒
+∞
→
y
1
x
y
x
)
x
1
(
log
y
5
+
=
⎪
⎩
⎪
⎨
⎧
−∞
→
⇒
=
⇒
=
⇒
=
⇒
−
=
−
+
=
−
→
+∞
→
⇒
=
⇒
+∞
=
⇒
+∞
=
⇒
∞
+
=
+∞
→
∞
−
∞
+
y
5
5
0
5
)
0
(
log
y
)
1
1
(
log
)]
1
(
1
[
log
y
:
1
x
Para
y
5
5
5
)
(
log
y
)
1
(
log
y
:
x
Para
y
y
5
5
5
y
y
5
5
Se 0 < a < 1 ⇒ Função
logarítmica decrescente
Para x
log
)
x
(
f
a
=
Para x
log
)
x
(
f
a
=
Se a > 1 ⇒ Função
logarítmica crescente
37](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-37-320.jpg)
![Gráfico de Uma Função Logarítmica
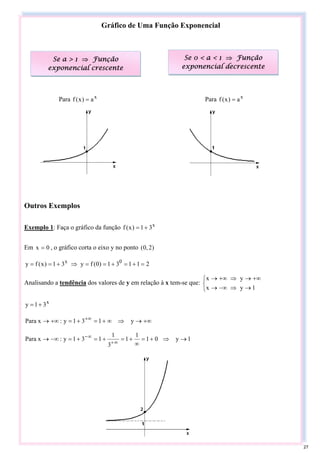
Exemplo 2: Faça o gráfico da função x
log
1
)
x
(
f 3
+
=
Rearranjando a função:
)
x
3
(
log
)
x
(
f
x
log
3
log
x
log
1
)
x
(
f 3
3
3
3
=
⇒
+
=
+
=
Em 0
y = , o gráfico corta o eixo x no ponto )
0
,
3
/
1
( :
3
/
1
x
x
3
1
x
3
3
)
x
3
(
log
0
)
x
3
(
log
)
x
(
f
y 0
3
3
=
⇒
=
⇒
=
⇒
=
⇒
=
=
Como 0
b > , tem-se: 0
x
0
x
3 >
⇒
> . Assim, o intervalo de valores que x pode assumir é [
,
0
] ∞
+ .
Analisando a tendência dos valores de y em relação à x tem-se que:
⎩
⎨
⎧
−∞
→
⇒
→
+∞
→
⇒
+∞
→
y
0
x
y
x
)
x
3
(
log
y
3
=
+∞
→
⇒
=
⇒
+∞
=
⇒
+∞
=
+∞
×
=
=
+∞
→ +∞
y
3
3
3
)
(
log
)]
(
3
[
log
)
x
3
(
log
y
:
x
Para y
y
3
3
3
−∞
→
⇒
=
⇒
=
⇒
=
⇒
=
×
=
→ −∞
y
3
3
0
3
)
0
(
log
y
)
0
(
log
)
0
3
(
log
y
:
0
x
Para y
y
3
3
3
Exemplo 3: Faça o gráfico da função )
x
2
(
log
)
x
(
f 4
/
1
+
=
Em 0
y = , o gráfico corta o eixo x no ponto )
0
,
1
(−
1
x
x
2
1
x
2
)
4
/
1
(
)
x
2
(
log
0
)
x
2
(
log
)
x
(
f
y 0
4
/
1
4
/
1
−
=
⇒
+
=
⇒
+
=
⇒
+
=
⇒
+
=
=
Como 0
b > , tem-se: 2
x
0
x
2 −
>
⇒
>
+ . O intervalo de valores que x pode assumir é [
,
2
] ∞
+
− .
Analisando a tendência dos valores de y em relação à x tem-se que:
⎩
⎨
⎧
+∞
→
⇒
−
→
−∞
→
⇒
+∞
→
y
2
x
y
x
)
x
2
(
log
y
4
/
1
+
=
−∞
→
⇒
=
⇒
+∞
=
⇒
+∞
=
⇒
∞
+
=
+∞
→ +∞
−
y
4
4
)
4
/
1
(
)
(
log
y
)
2
(
log
y
:
x
Para y
y
4
/
1
4
/
1
+∞
→
⇒
=
⇒
=
⇒
=
⇒
=
⇒
−
+
=
−
→ −∞
−
−
y
4
4
0
4
0
)
4
/
1
(
)
0
(
log
y
)]
2
(
2
[(
log
y
:
2
x
Para y
y
y
4
/
1
4
/
1
38](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-38-320.jpg)
![Gráfico de Uma Função Logarítmica
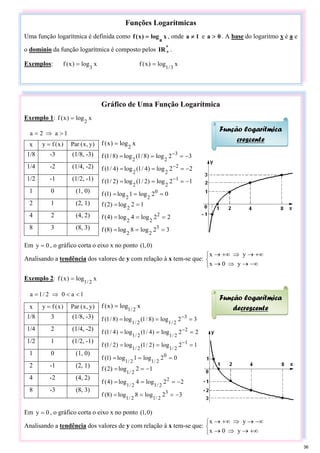
Exemplo 4: Faça o gráfico da função x
log
1
)
x
(
f 3
−
=
Rearranjando a função:
x
3
log
x
log
3
log
x
log
1
)
x
(
f 3
3
3
3
=
−
=
−
=
)
x
/
3
(
log
x
log
3
log
x
log
1
)
x
(
f 3
3
3
3
=
−
=
−
=
)
3
/
x
(
log
)
1
(
)
3
/
x
(
log
)
x
/
3
(
log
)
x
(
f 3
1
3
3
×
−
=
=
= −
Fazendo uma mudança de base:
3
log
)
3
/
x
(
log
)
1
(
)
3
/
x
(
log
)
1
(
)
x
(
f 3
×
−
=
×
−
=
1
3
log
)
3
/
x
(
log
3
log
)
1
(
)
3
/
x
(
log
3
log
)
3
/
x
(
log
)
1
(
)
x
(
f
−
=
×
−
=
×
−
=
)
3
/
x
(
log
3
log
)
3
/
x
(
log
)
x
(
f 1
3
1 −
=
= −
)
3
/
x
(
log
)
x
(
f 3
/
1
=
Em 0
y = , o gráfico corta o eixo x no ponto )
0
,
3
(
3
x
3
/
x
1
3
/
x
)
3
/
1
(
)
3
/
x
(
log
0
)
3
/
x
(
log
)
x
(
f
y 0
3
/
1
3
/
1
=
⇒
=
⇒
=
⇒
=
⇒
=
=
Para 0
x
0
3
/
x >
⇒
> . O intervalo de valores que x pode assumir é [
,
0
] ∞
+ .
Analisando a tendência dos valores de y em relação à x tem-se que:
⎩
⎨
⎧
+∞
→
⇒
→
−∞
→
⇒
+∞
→
y
0
x
y
x
)
3
/
x
(
log
y
3
/
1
=
−∞
→
⇒
=
⇒
+∞
=
⇒
+∞
=
⇒
+∞
=
+∞
→ +∞
−
y
3
3
)
3
/
1
(
)
(
log
y
)
3
/
(
log
y
:
x
Para y
y
3
/
1
3
/
1
+∞
→
⇒
=
⇒
=
⇒
=
⇒
=
⇒
=
→ −∞
−
−
y
3
3
0
3
0
)
3
/
1
(
)
0
(
log
y
)
3
/
0
(
log
y
:
0
x
Para y
y
y
3
/
1
3
/
1
39](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-39-320.jpg)








![Inequações Produto e Quociente e Sistemas de Inequações
Exemplo 6: Resolva a inequação 0
)
5
x
( 3
<
+
Para que a função 3
)
5
x
(
)
x
(
f +
= seja negativa, é necessário que a valor de )
5
x
( + seja negativo, pois
essa soma tem expoente ímpar. Bases negativas de expoente ímpar resultam em valores negativos.
Assim:
5
x
0
5
x
−
<
<
+
Exemplo 7: Resolva a inequação 13
7
x
2
1 ≤
+
<
−
Para se resolver inequações do primeiro grau do tipo simultânea (com duas desigualdades) deve-se
isolar x na desigualdade:
3
x
4
2
6
x
2
8
6
x
2
8
7
13
x
2
7
1
13
7
x
2
1
≤
<
−
≤
<
−
≤
<
−
−
≤
<
−
−
≤
+
<
−
Exemplo 8: Resolva a inequação 5
3
x
1 ≤
+
−
<
Isolando x na desigualdade:
2
x
2
3
5
x
3
1
5
3
x
1
≤
−
<
−
−
≤
−
<
−
≤
+
−
<
Exemplo 9: Resolva o sistema
⎩
⎨
⎧
+
≤
−
+
>
+
5
x
1
x
2
7
x
10
x
2
Cada inequação é resolvida separadamente:
3
x
10
7
x
x
2
7
x
10
x
2
)
x
(
f 1
−
>
−
>
−
+
>
+
=
6
x
1
5
x
x
2
5
x
1
x
2
)
x
(
f 2
≤
+
≤
−
+
≤
−
=
Os valores de x que satisfazem a inequação 0
)
5
x
( 3
≥
+ , fazendo com
que seu resultado seja menor que zero, são: }
5
x
/
IR
x
{
S −
<
∈
= .
Os valores de x que satisfazem a inequação simultânea, fazendo
com que a substituição de “x” em 7
x
2 + resulte em um valor
pertencente ao intervalo ] ]
13
,
1
− , são: }
3
x
4
/
IR
x
{
S ≤
<
−
∈
= .
O sentido da desigualdade é
invertido quando a inequação
é multiplicada por (-1).
Os valores de x que satisfazem a inequação simultânea 5
3
x
1 ≤
+
−
< , fazendo
com que seu resultado pertença ao intervalo ] ]
5
,
1 , são: }
2
x
2
/
IR
x
{
S <
≤
−
∈
= .
Multiplicando por 1)
(− :
2
x
2
ou
2
x
2
<
≤
−
−
≥
>
+
Os valores de x devem satisfazer as
duas inequações do sistema. Para tal,
é feita uma intersecção das soluções
encontradas para cada inequação.
Os valores de x que satisfazem o sistema de
inequações, fazendo com que 7
x
10
x
2 +
>
+ e
5
x
1
x
2 +
≤
− , são: }
6
x
3
/
IR
x
{
S ≤
<
−
∈
= .
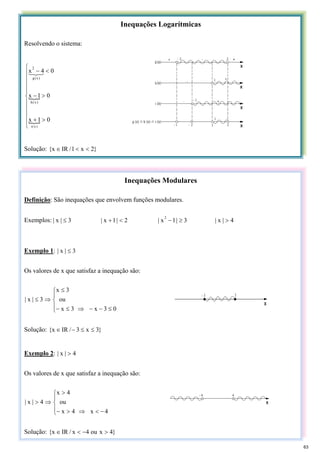
50](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-50-320.jpg)

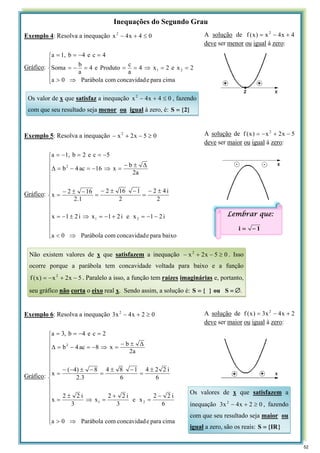
![Inequações do Segundo Grau
Exemplo 7: Resolva a inequação 14
x
5
x
0 2
≤
−
<
Primeiramente, resolve-se o sistema:
⎩
⎨
⎧
−
−
=
−
=
⇒
⎩
⎨
⎧
≤
−
−
>
−
⇒
⎩
⎨
⎧
≤
−
>
−
14
x
5
x
)
x
(
f
x
5
x
)
x
(
f
0
14
x
5
x
0
x
5
x
14
x
5
x
0
x
5
x
2
2
2
1
2
2
2
2
Solução de 1
)
x
(
f : x
5
x
)
x
(
f 2
1 −
=
Gráfico:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⇒
>
=
=
⇒
=
=
=
−
=
=
−
=
=
cima
para
e
concavidad
com
Parábola
0
a
5
x
e
0
x
0
a
c
Produto
e
5
a
b
Soma
0
c
e
5
b
1,
a
2
1
Solução de 2
)
x
(
f : 14
x
5
x
)
x
(
f 2
2 −
−
=
Gráfico:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
⇒
>
=
−
=
⇒
−
=
=
−
=
−
=
−
=
=
cima
para
e
concavidad
com
Parábola
0
a
7
x
e
2
x
14
Produto
e
5
a
b
Soma
14
c
e
5
b
1,
a
2
1
Na reta dos reais e fazendo a intersecção:
Exemplo 8: Resolva a inequação ( )( ) 0
6
x
7
x
7
x
2
x 2
2
≤
+
−
+
+
Estudam-se os sinais de cada função ( ) ( ) 0
6
x
7
x
7
x
2
x
2
2
1
2
)
x
(
f
)
x
(
f
≤
+
−
+
+ 4
43
4
42
1
4
43
4
42
1
separadamente:
Solução de 1
)
x
(
f : 7
x
2
x
)
x
(
f 2
1 +
+
=
Gráfico:
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎨
⎧
⇒
>
−
=
+
=
⇒
±
=
±
=
×
±
−
=
−
±
−
=
−
±
−
=
Δ
±
−
=
⇒
−
=
−
=
Δ
=
=
=
cima
para
e
concavidad
com
Parábola
0
a
i
6
1
x
e
i
6
1
x
i
6
1
x
2
i
6
2
2
2
i
6
4
2
x
2
1
24
2
1
.
2
24
2
x
a
2
b
x
24
ac
4
b
7
c
e
2
b
,
1
a
2
1
2
A solução de x
5
x
)
x
(
f 2
1 −
=
deve ser maior que zero:
A solução de 14
x
5
x
)
x
(
f 2
2 −
−
=
deve ser maior que zero:
Os valores de x que satisfazem a
inequação 14
x
5
x
0 2
≤
−
< , fazendo com
que o resultado da função x
5
x
)
x
(
f 2
−
=
pertença ao intervalo ] ]
14
,
0 , são:
}
7
x
5
ou
0
x
2
/
IR
x
{
S ≤
<
<
≤
−
∈
=
A solução de 7
x
2
x
)
x
(
f 2
1 +
+
=
deve ser menor ou igual à zero:
53](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-53-320.jpg)



![Inequações Exponenciais
Outros exemplos:
Exemplo 3: 1
9 2
x
x
2
≥
−
[ ] 0
x
x
3
3
3
)
3
(
1
9
2
0
x
x
0
2
x
x
2
2
x
x
2
2
2
≥
−
⇒
≥
⇒
≥
⇒
≥
−
−
−
⎩
⎨
⎧
=
=
⇒
−
=
1
x
0
x
raízes
com
grau
º
2
do
Função
x
x
)
x
(
g
2
1
2
Solução: }
1
x
ou
0
x
/
IR
x
{ ≥
≤
∈
Exemplo 4:
x
4
x
x
2
64
2
2
2
−
−
⋅
>
⋅
0
6
x
5
x
x
4
6
x
x
2
2
2
2
2
2
64
2
2
2
2
x
4
6
x
x
x
4
6
x
x
x
4
x
x
2
2
2
>
−
+
−
⇒
−
>
+
−
⇒
>
⇒
⋅
>
⇒
⋅
>
⋅
−
+
−
−
+
−
−
−
⎩
⎨
⎧
=
=
⇒
−
+
−
=
3
x
2
x
raízes
com
grau
º
2
do
função
6
x
5
x
)
x
(
g
2
1
2
Solução: }
3
x
2
/
IR
x
{ <
<
∈
Exemplo 5: 90
3
3
x
2
x
≤
+
+
0
2
x
2
x
3
3
3
10
10
3
3
10
)
1
9
(
3
3
10
3
9
3
9
10
3
3
3
90
3
3
2
x
2
x
2
x
2
x
x
x
2
x
x
2
x
≤
−
⇒
≤
⇒
≤
⋅
≤
⋅
⇒
⋅
≤
+
⇒
⋅
≤
+
⋅
⇒
⋅
≤
+
⋅
⇒
≤
+
+
{ 2
x
raiz
com
grau
1º
do
Função
2
x
g(x) =
⇒
−
=
Solução: }
2
x
/
IR
x
{ ≤
∈
Exemplo 6:
4
x
2
x
4
27
8
2
3
+
+
⎟
⎠
⎞
⎜
⎝
⎛
>
⎟
⎠
⎞
⎜
⎝
⎛
0
2
x
2
x
14
x
7
12
x
3
2
x
4
2
3
2
3
2
3
2
3
3
2
2
3
27
8
2
3
12
x
3
2
x
4
4
x
3
2
x
4
4
x
3
2
x
4
4
x
2
x
4
>
+
⇒
−
>
⇒
−
>
⇒
−
−
>
+
⎟
⎠
⎞
⎜
⎝
⎛
>
⎟
⎠
⎞
⎜
⎝
⎛
⇒
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
>
⎟
⎠
⎞
⎜
⎝
⎛
⇒
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
>
⎟
⎠
⎞
⎜
⎝
⎛
⇒
⎟
⎠
⎞
⎜
⎝
⎛
>
⎟
⎠
⎞
⎜
⎝
⎛
−
−
+
+
−
+
+
+
+
+
{ 2
x
raiz
com
grau
1º
do
Função
2
x
g(x) −
=
⇒
+
=
Solução: }
2
x
/
IR
x
{ −
>
∈
58](https://image.slidesharecdn.com/mapamentaltodasasmaterias-211008201843/85/Mapa-mental-todas-as-materias-58-320.jpg)