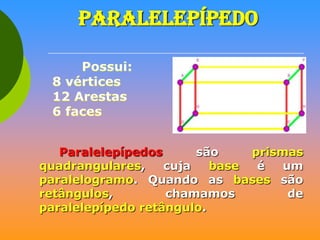
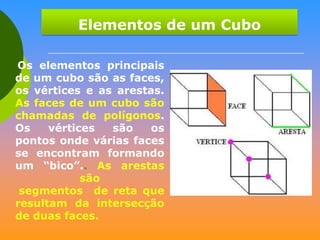
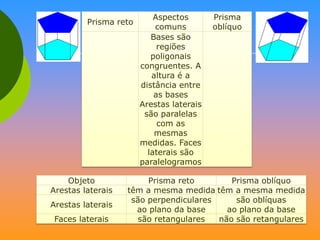
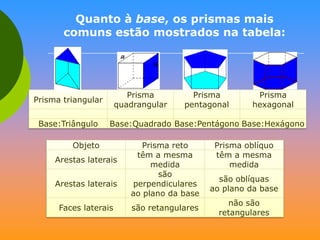
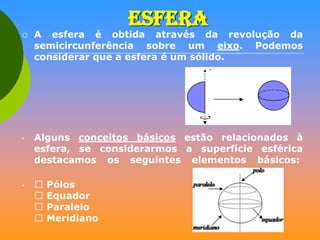
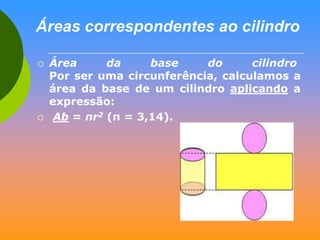
O documento discute vários sólidos geométricos como cubos, paralelepípedos, prismas, pirâmides, cilindros, cones e esferas. Ele fornece definições e exemplos de cada um destes sólidos, destacando suas propriedades geométricas e aplicações na arquitetura, engenharia e outros campos.