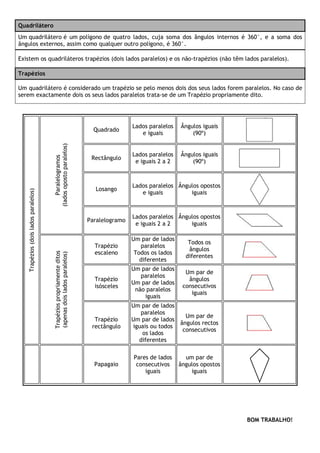
(1) O documento discute os conceitos de quadriláteros, incluindo suas propriedades e tipos. (2) Quadriláteros podem ser côncavos ou convexos e têm quatro lados. (3) Existem diferentes tipos de quadriláteros definidos por suas propriedades geométricas, como trapézios, paralelogramos, losangos, retângulos e quadrados.

1. ESCOLA SECUNDÁRIA COM 2º E 3º CICLOS ANSELMO DE ANDRADE
ANO LECTIVO 2009-2010
MATEMÁTICA 7º ANO DE ESCOLARIDADE
NOME: ___________________________________________ Nº: ____ DATA: ___/___/___
Quadriláteros
(1) Um quadrilátero é um polígono com ___________ lados.
(2) Nas figuras ao lado estão representados dois
quadriláteros: - um côncavo e um convexo.
(2.1) A Figura 1 representa um
quadrilátero ____________.
(2.2) A Figura 2 representa um
quadrilátero ____________.
(3) Na Figura 3 está representado um quadrilátero [ABCD].
(3.1) Os lados [AB] e [BC] têm um vértice comum. Chamam-se, por
isso, lados consecutivos. São também consecutivos os lados _____ e
_____; _____ e _____; _____ e _____.
(3.2) Os lados [AD] e [BC] não têm nenhum vértice comum. Por isso,
chamam-se lados opostos. São também lados opostos _____ e _____.
(4) Observa as figuras.
(4.1) Os ângulos BAD e ADC dizem-se
ângulos adjacentes ao lado [AD] do
quadrilátero da Figura 4. Os ângulos
ABC e BCD são adjacentes ao lado
_____ , os ângulos ________ e ________
são adjacentes ao lado [AB] e os
ângulos BCD e ________ são
adjacentes ao lado [DC].
(4.2) Os ângulos EFG e EHD assinalados no quadrilátero representado na Figura 5,
dizem-se ângulos opostos. São também ângulos opostos os ângulos ________ e ________.
(5) Observa a figura.
(5.1) Os segmentos de recta que unem dois vértices não
consecutivos chamam-se diagonais. As diagonais do
quadrilátero representado na Figura 6 são os segmentos de
recta _____ e _____.

2. (6) Observa os seguintes quadriláteros.
(6.1) Traça as diagonais em cada um dos quadriláteros representados.
(6.2) Num quadrilátero podem traçar-se, no máximo, ______ diagonais.
(7) Na Figura 8 estão representados um quadrilátero e duas rectas r e s.
Se conseguirmos dobrar uma figura segundo uma
recta e as duas partes ficarem exactamente
coincidentes, diz-se que essa recta é um eixo de
simetria da figura.
Os eixos de simetria do quadrilátero representado são as rectas ____ e ____.
(8) Na figura abaixo encontram-se representados quatro quadriláteros. Em cada um deles traça os
possíveis eixos de simetria.
(9) Observa a resposta à pergunta anterior e preenche o seguinte quadro:
Quadrilátero Número de eixos de simetria
Quadrado
Losango
Paralelogramo
Trapézio isósceles
(10) Qualquer quadrilátero pode ser decomposto em dois triângulos traçando-se uma das suas
diagonais. Observa a Figura 9, como exemplo.
Sabes que a soma das amplitudes dos ângulos internos de
um triângulo é igual a 180º. Como podemos decompor
qualquer quadrilátero em dois triângulos, através de
uma das suas diagonais, então a soma de todos os
ângulos internos de um quadrilátero é igual a ______.

3. (11) Considera os polígonos seguintes.
Indica:
(11.1) os quadriláteros;
(11.2) os trapézios;
(11.3) os paralelogramos;
(11.4) os losangos;
(11.5) os rectângulos;
(11.6) os quadrados.
(12) Observa os polígonos representados na figura seguinte.
(13.1) Traça as diagonais para cada um dos polígonos.
(13.2) Completa o quadro com V (verdadeiro) ou F (falso).
Polígono As minhas diagonais
bissectam-se
As minhas diagonais
são perpendiculares
As minhas diagonais
têm o mesmo comprimento
A
B
C
D
E
F
(13.3) Identifica cada um dos polígonos:
A____________________ B____________________ C____________________
D____________________ E____________________ F____________________

4. Quadrilátero
Um quadrilátero é um polígono de quatro lados, cuja soma dos ângulos internos é 360°, e a soma dos
ângulos externos, assim como qualquer outro polígono, é 360°.
Existem os quadriláteros trapézios (dois lados paralelos) e os não-trapézios (não têm lados paralelos).
Trapézios
Um quadrilátero é considerado um trapézio se pelo menos dois dos seus lados forem paralelos. No caso de
serem exactamente dois os seus lados paralelos trata-se de um Trapézio propriamente dito.
Quadrado
Lados paralelos
e iguais
Ângulos iguais
(90º)
Rectângulo
Lados paralelos
e iguais 2 a 2
Ângulos iguais
(90º)
Losango
Lados paralelos
e iguais
Ângulos opostos
iguais
Paralelogramos
(ladosopostoparalelos)
Paralelogramo
Lados paralelos
e iguais 2 a 2
Ângulos opostos
iguais
Trapézio
escaleno
Um par de lados
paralelos
Todos os lados
diferentes
Todos os
ângulos
diferentes
Trapézio
isósceles
Um par de lados
paralelos
Um par de lados
não paralelos
iguais
Um par de
ângulos
consecutivos
iguais
Trapézios(doisladosparalelos)
Trapéziospropriamenteditos
(apenasdoisladosparalelos)
Trapézio
rectângulo
Um par de lados
paralelos
Um par de lados
iguais ou todos
os lados
diferentes
Um par de
ângulos rectos
consecutivos
Papagaio
Pares de lados
consecutivos
iguais
um par de
ângulos opostos
iguais
BOM TRABALHO!