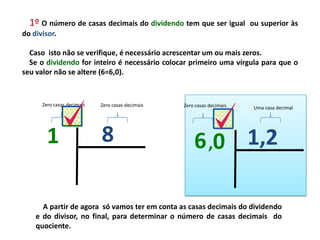
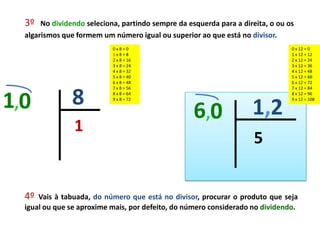
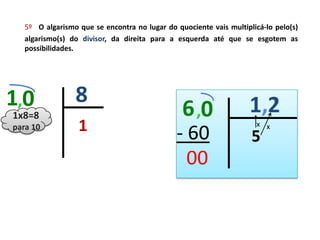
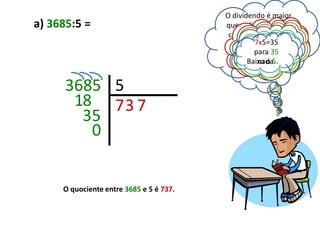
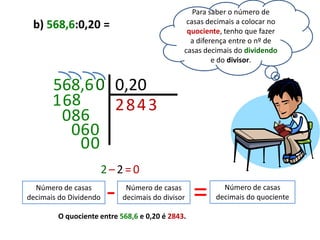
Este documento fornece instruções para realizar divisões, explicando os passos: 1) garantir que o dividendo tenha casas decimais iguais ou superiores ao divisor, 2) garantir que o dividendo seja maior ou igual ao divisor, 3) selecionar algarismos do dividendo para formar um número maior ou igual ao divisor e encontrar o quociente correspondente na tabuada, repetindo o processo com os restos até zerar.

1. Algoritmo
da DIVISÃO

2. Antes de pensar no algoritmo da divisão
é necessário saber a tabuada.
Sem saber multiplicar, é impossível saber
dividir.
Precisas de saber a tabuada do número
que está no divisor desde o 0 até 9.

3.  56 é o Dividendo
 14 é o divisor
 4 é o quociente
 0 é o resto

4. 1º O número de casas decimais do dividendo tem que ser igual ou superior às
do divisor.
Caso isto não se verifique, é necessário acrescentar um ou mais zeros.
Se o dividendo for inteiro é necessário colocar primeiro uma vírgula para que o
seu valor não se altere (6=6,0).
Zero casas decimais Zero casas decimais Zero casas decimais Uma casa decimal
1 8 6 ,0 1,2
A partir de agora só vamos ter em conta as casas decimais do dividendo
e do divisor, no final, para determinar o número de casas decimais do
quociente.

5. Esquece as virgulas!
2º O dividendo tem que ser maior ou igual que o divisor, se não for, é necessário
acrescentar zero(s).
Para o cálculo
considera-se 10.
Para o cálculo Para o cálculo
consideras 60. consideras 12.
1 ,0 8
6 ,0 1,2

6. 3º No dividendo seleciona, partindo sempre da esquerda para a direita, o ou os
algarismos que formem um número igual ou superior ao que está no divisor.
0x8=0 0 x 12 = 0
1x8=8 1 x 12 = 12
2 x 8 = 16 2 x 12 = 24
3 x 8 = 24 3 x 12 = 36
4 x 8 = 32 4 x 12 = 48
5 x 8 = 40 5 x 12 = 60
6 x 8 = 48 6 x 12 = 72
7 x 8 = 56 7 x 12 = 84
1,0 8 8 x 8 = 64
9 x 8 = 72
1,2
8 x 12 = 96
9 x 12 = 108
6,0
1
5
4º Vais à tabuada, do número que está no divisor, procurar o produto que seja
igual ou que se aproxime mais, por defeito, do número considerado no dividendo.

7. 5º O algarismo que se encontra no lugar do quociente vais multiplicá-lo pelo(s)
algarismo(s) do divisor, da direita para a esquerda até que se esgotem as
possibilidades.
1,0 8
1x8=8
para 10 1 x x

8. 1,00 0 8 6 ,0 1,2
20 1 25 - 60 5
40 00
0
6º - A seguir subtrais esse número ao número com que estás a trabalhar
no dividendo.
A diferença nunca pode ser igual ou superior ao número que está no
divisor.
De cada vez que baixas um algarismo do dividendo obténs
um novo número e começas a pensar tudo como da primeira
vez.

9. 7º- O número de casas decimais a colocar no quociente determina-se da
seguinte forma:
Número de casas
decimais do dividendo - Número de casas
decimais do divisor
1,00 0 8 6 ,0 1,2
20 0, 125 - 60 5
40
0 00

10. Calcula os seguintes
quocientes e confirma
a seguir os resultados.
a) 3685:5 = b) 568,6:0,20 = c) 34230:35 =

11. O dividendo é maior
a) 3685:5 = que o divisor, posso
Em 18
começarEm 35
a divisão.
7x5=35
Então, em para
7x5=35 36,
quantas
3x5=15 para
quantas
Baixo 1 8.
36 é o
vezes355?
parahá
vezes há 35?
quantas 18 sãohá 5?
vezes 5.
Baixo o3.
nada.
Há
HáHá 7x.
7x.
3685 5
18 7 3 7
35
0
O quociente entre 3685 e 5 é 737.

12. Para saber o número de
casas decimais a colocar no
b) 568,6:0,20 = quociente, tenho que fazer
a diferença entre o nº de
casas decimais do dividendo
e do divisor.
568,6 0 0,20
1 68 2843
0 86
06 0
00
2–2=0
Número de casas
decimais do Dividendo - Número de casas
decimais do divisor = Número de casas
decimais do quociente
O quociente entre 568,6 e 0,20 é 2843.

13. c) 34230:35 =
34230 35
27 3 9 7 8
2 80
00
O quociente entre 34230 e 35 é 978.