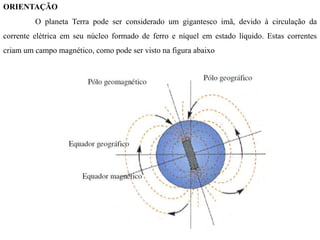
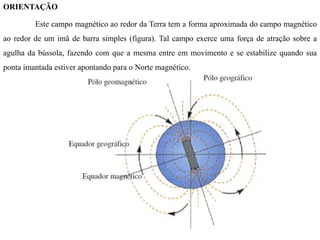
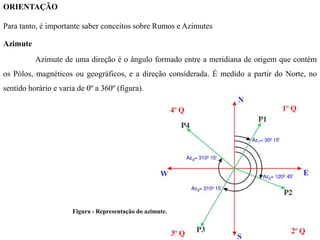
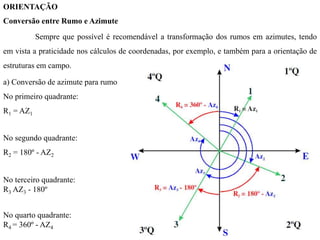
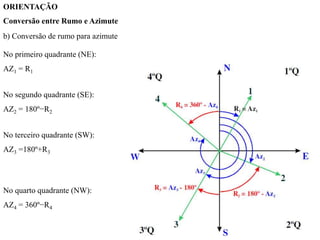
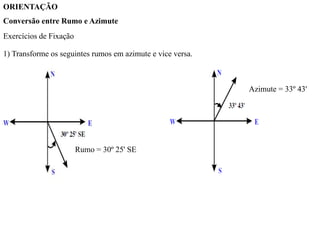
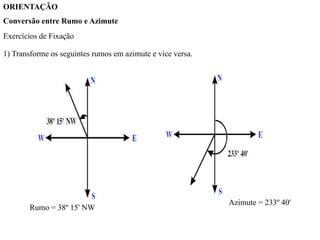
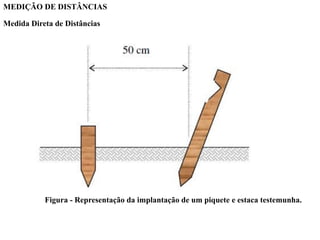
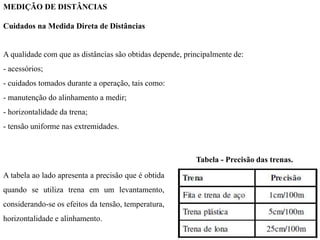
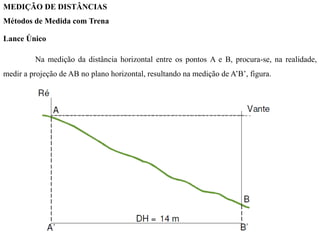
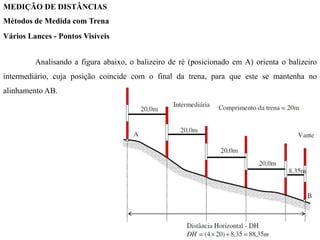
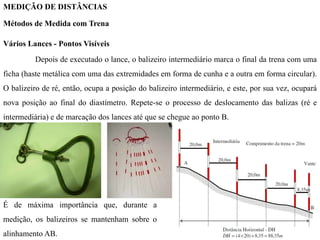
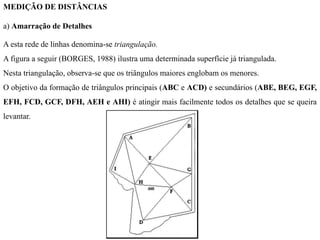
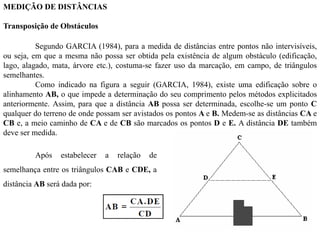
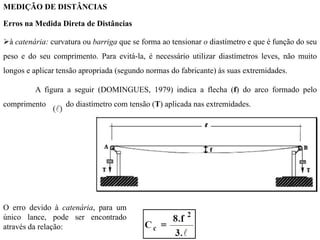
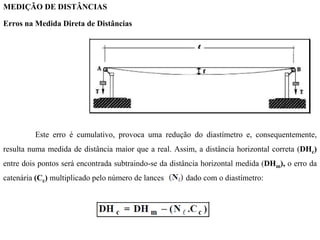
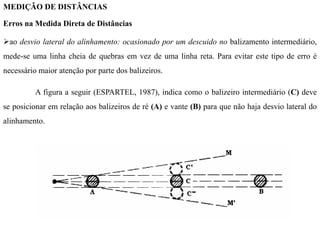
O documento discute conceitos de orientação, azimute e rumo, e medição de distâncias em topografia. Explica que a orientação na topografia se refere aos sistemas geográfico e magnético, e como converter entre azimute e rumo. Também descreve métodos de medição de distâncias diretas utilizando trenas, incluindo cuidados, precisão e uso de acessórios como piquetes e balizas.