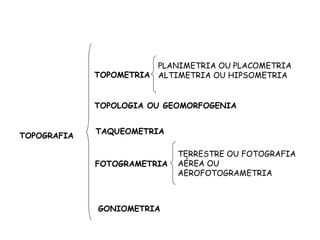
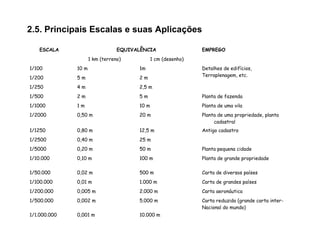
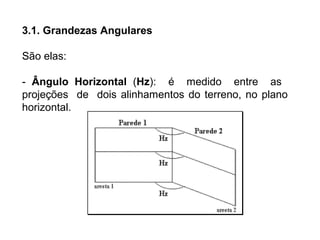
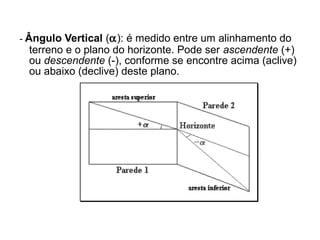
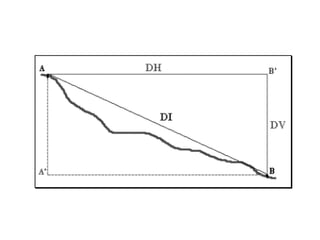
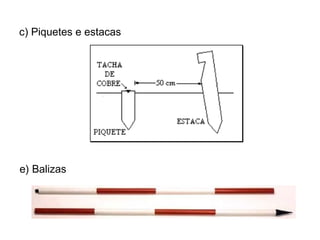
O documento discute conceitos gerais de topografia, definindo-a como a descrição exata e minuciosa de um lugar. Detalha os principais métodos de medição topográfica, incluindo planimetria, altimetria, fotogrametria e os erros associados a cada método. Também explica as unidades de medida, escalas e instrumentos usados em levantamentos topográficos.

1. CONCEITOS GERAIS

4. TOPOGRAFIA
Definição:
Importância:
a palavra "Topografia" deriva das palavras gregas
"topos" (lugar) e "graphen" (descrever), o que significa,
a descrição exata e minuciosa de um lugar.
ela é a base de qualquer projeto e de qualquer obra
realizada por engenheiros ou arquitetos.

5. TOPOGRAFIA
TOPOMETRIA
PLANIMETRIA OU PLACOMETRIA
ALTIMETRIA OU HIPSOMETRIA
TOPOLOGIA OU GEOMORFOGENIA
TAQUEOMETRIA
FOTOGRAMETRIA
TERRESTRE OU FOTOGRAFIA
AÉREA OU
AEROFOTOGRAMETRIA
GONIOMETRIA

6. TOPOMETRIA:
A Topometria trata de medidas das grandezas lineares e
angulares que definem a posição dos pontos topográficos,
tanto nos planos horizontais e/ou verticais.
A – Planimetria:
Na Planimetria, as medidas, tanto lineares como angulares,
são efetuadas em planos horizontais, obtendo-se ângulos e
distâncias horizontais, não levando em consideração o
relevo.
B. - Altimetria:
As medidas são efetuadas num plano vertical, onde se
obtêm os ângulos azimutais e verticais e as distâncias
horizontais e verticais (diferença de nível).

7. TOPOLOGIA:
Os trabalhos da altimetria juntado a planimetria dão origem
às plantas planialtimétricas.
FOTOGRAMETRIA:
A Aerofotogrametria é o método de levantamento utilizado
para grandes glebas de Terra. Emprega aparelhagens
moderníssimas, e cada vez mais aperfeiçoadas, acopladas
em aviões, fornecendo fotografias orientadas da superfície
da Terra, que podem ser de dois tipos: eixos verticais e
inclinados.

10. 1.1.3. ERROS EM TOPOGRAFIA
a) Naturais: são aqueles ocasionados por fatores ambientais
b) Instrumentais: são aqueles ocasionados por defeitos ou
imperfeições dos instrumentos ou aparelhos utilizados nas
medições.
c) Pessoais: são aqueles ocasionados pela falta de cuidado do
operador.
c.1) catenária:
c.2) verticalidade das balizas:
c.3) Horizontalidade do diastímetro:
c.4) Desvio do alinhamento:

11. DESENHO TOPOGRÁFICO E ESCALA

12.  O desenho topográfico nada mais é do que a projeção de todas as
medidas obtidas no terreno sobre o plano do papel.
 Neste desenho, os ângulos são representados em verdadeira
grandeza (VG) e as distâncias são reduzidas segundo uma razão
constante.
"L" = representa qualquer comprimento linear real, medido sobre o terreno.
"" = representa um comprimento linear gráfico qualquer, medido sobre o papel, e
que correspondente ao comprimento medido sobre o terreno.
"M" = é denominado Título ou Módulo da escala e representa o inverso de ( / L).

13. A escala pode ser apresentada sob a forma de:
- fração : 1/100, 1/2000 etc. ou
-proporção : 1:100, 1:2000 etc.
Podemos dizer ainda que a escala é:
- de ampliação : quando  > L (Ex.: 2:1)
- natural : quando  = L (Ex.: 1:1)
- de redução : quando  < L (Ex.: 1:50)

14. 2.1 Escala natural
A escala natural é quando o desenho for do mesmo tamanho
da peça. Teremos a escala assim representadas:
1:1 – (escala um por um)
Ex: uns lápis, uma borracha, podem ser desenhados no mesmo
tamanho, isto é, escala 1:1
2.2 Escala de redução
A escala é de redução quando o desenho de um objeto,
por exemplo, uma casa, um armário, um mapa, for feito menor que
o tamanho do mesmo.
Exemplo: o desenho de uma cadeira terá que ser reduzido para
caber no papel. Ex. 1:2, 1:50
.
Embora o desenho esteja reduzido as medidas continuam reais.

15. 2.3 Escala de ampliação
A escala é de ampliação quando o objeto real é pequeno, e se deseja
desenhar em tamanho maior.
Uma peça de relógio, por exemplo: 5:1, 10:1
Desenho - 5:1 - objeto

16. 2.5. Principais Escalas e suas Aplicações
ESCALA EQUIVALÊNCIA EMPREGO
1 km (terreno) 1 cm (desenho)
1/100 10 m 1m Detalhes de edifícios,
Terraplenagem, etc.
1/200 5 m 2 m
1/250 4 m 2,5 m
1/500 2 m 5 m Planta de fazenda
1/1000 1 m 10 m Planta de uma vila
1/2000 0,50 m 20 m Planta de uma propriedade, planta
cadastral
1/1250 0,80 m 12,5 m Antigo cadastro
1/2500 0,40 m 25 m
1/5000 0,20 m 50 m Planta pequena cidade
1/10.000 0,10 m 100 m Planta de grande propriedade
1/50.000 0,02 m 500 m Carta de diversos países
1/100.000 0,01 m 1.000 m Carta de grandes países
1/200.000 0,005 m 2.000 m Carta aeronáutica
1/500.000 0,002 m 5.000 m Carta reduzida (grande carta inter-
Nacional do mundo)
1/1.000.000 0,001 m 10.000 m

17. GRANDEZAS MEDIDAS EM UM
LEVANTAMENTO TOPOGRÁFICO

18. 3.1. Grandezas Angulares
São elas:
- Ângulo Horizontal (Hz): é medido entre as
projeções de dois alinhamentos do terreno, no plano
horizontal.

19. - Ângulo Vertical (α): é medido entre um alinhamento do
terreno e o plano do horizonte. Pode ser ascendente (+)
ou descendente (-), conforme se encontre acima (aclive)
ou abaixo (declive) deste plano.

20. 3.2. Grandezas Lineares
São elas:
- Distância Horizontal (DH):
- Distância Inclinada (DI):
é a distância medida entre dois pontos, no plano horizontal.
- Distância Vertical ou Diferença de Nível (DV ou DN):
é a distância medida entre dois pontos, num plano vertical
que é perpendicular ao plano horizontal.
é a distância medida entre dois pontos, em planos que
seguem a inclinação da superfície do terreno.

22. UNIDADES DE MEDIDA
Em Topografia, são medidas duas espécies de grandezas,
as lineares e as angulares, mas, na verdade, outras duas
espécies de grandezas são também trabalhadas, as de
superfície e as de volume.

23. 4.1. Unidades de Medida Linear
 1 polegada = 2,75 cm = 0,0275 m
 1 polegada inglesa = 2,54 cm = 0,0254 m
 1 pé = 30,48cm = 0,3048 m
 1 jarda = 91,44cm = 0,9144m
 1 milha brasileira = 2200 m
 1 milha terrestre/inglesa = 1609,31 m
4.2. Unidades de Medida Angular
 Para as medidas angulares têm-se a seguinte relação:
360º = 400g = 2 π

24. 4.3. Unidades de Medida de Superfície
 1 are = 100 m2
 1 acre = 4.046,86 m2
 1 hectare (ha) = 10.000 m2
 1 alqueire paulista (menor) = 2,42 ha = 24.200 m2
 1 alqueire mineiro (geométrico) = 4,84 ha = 48.400 m2
4.4. Unidades de Medida de Volume
 litro = 0,001 m3

25. MEDIÇÃO DE DISTÂNCIAS

26. 5.1. MÉTODO DE MEDIÇÃO DE DISTÂNCIAS HORIZONTAIS:
♦ - medidas diretas: uma medida é considerada ‘direta’ se o
instrumento usado na medida apoiar-se no terreno ao
longo do alinhamento, ou seja, se for aplicado no terreno
ao longo do alinhamento;
♦ - medidas indiretas: uma medida é considerada ‘indireta’
no caso da obtenção do comprimento de um
alinhamento através de medida de outras grandezas
com ele relacionada matematicamente;
♦ - medidas eletrônicas: é o caso do comprimento de um
alinhamento ser obtido através de instrumento que
utilizam o comprimento de onda do espectro
eletromagnético ou através de dados emitidos por
satélites.

27. 5.2 DISPOSITIVOS UTILIZADOS NA MEDIÇÃO DE
DISTÂNCIAS
a) Fita e Trena de Aço

28. b)Trena de Fibra de Vidro

29. c) Piquetes e estacas
e) Balizas

30. 5.4. Métodos de Medida com Diastímetros

31. 5.4.2 VÁRIOS LANCES - PONTOS VISÍVEIS

32. 5.4.3 Traçado de Perpendiculares
b.1)Triângulo Retângulo
 Este método consiste em passar por um ponto A, de um
alinhamento AB conhecido, uma perpendicular.
 Utilizando-se os doze (12) primeiros metros de uma
trena, dispõe-se, respectivamente, dos lados 3, 4 e 5
metros de um triângulo retângulo.

33. • Como indicado na figura abaixo, o 0 e 12 metros
estariam coincidentes em C, situado a 3 metros do ponto
A. O 7 metro (soma dos lados 3 e 4) e representado pelo
ponto D, se ajusta facilmente em função dos pontos A e C
já marcados

34. b.2)Triângulo Isósceles
 Como indicado na figura abaixo, o 0 e 12 metros estariam
coincidentes em C. O 2 m estaria sobre o alinhamento AB à
esquerda de C, definindo o ponto D. O 10 metro estaria sobre o
alinhamento AB à direita de C, definindo o ponto E. O ponto F,
definido pelo 6 metro, se ajusta facilmente em função dos pontos D
e E já marcados.

35. 5.4.4. Transposição de Obstáculos
5.4.4.1 Pontos extremos do alinhamento não intervisíveis
Assim, para que a distância AB possa ser determinada, escolhe-se um ponto
C qualquer do terreno de onde possam ser avistados os pontos A e B.
Medem-se as distâncias CA e CB e, a meio caminho de CA e de CB são
marcados os pontos D e E. A distância DE também deve ser medida.

36. 5.4.4.2 Pontos extremos do alinhamento visíveis
A medida de um alinhamento que corta um brejo, um lago, uma lagoa,
ou uma depressão ou uma voçoroca exige que se contorne o
obstáculo, através de perpendiculares e paralelas obtidas por ângulos
retos podem ser demarcadas com corrente e baliza, utilizando-se os
processos dos triângulos retângulos ou isósceles

37. 5.4.2 Erros de aferição da trena
n
m
r
l
cxl
l =
onde:
lr = comprimento real da linha;
c = comprimento da trena é o valor encontrado ao
compará-la como uma trena correta;
lm = comprimento medido com a trena não aferida;
ln = comprimento nominal da trena represento o valor
que ele deveria ter.