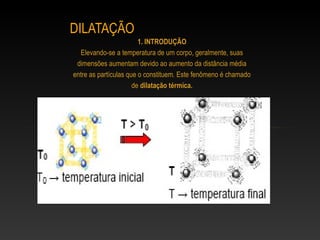
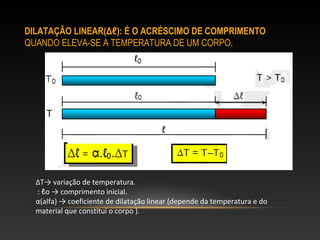
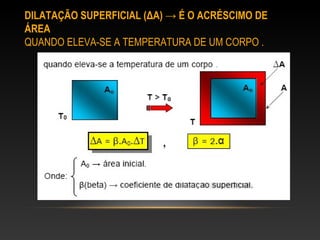
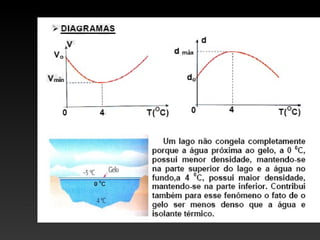
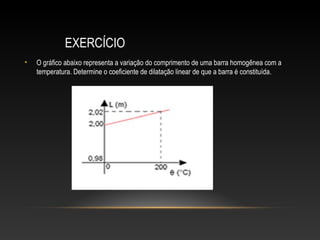
O documento discute os conceitos de dilatação térmica em materiais. A dilatação térmica ocorre quando um corpo aquece e suas dimensões aumentam devido ao aumento da distância média entre as partículas. Isso inclui a dilatação linear, superficial e volumétrica. O documento também aborda juntas de dilatação em construções e exemplos de exercícios sobre o cálculo da dilatação.

1. FÍSICA
fenômenos da Dilatação
Professora : Adrianne Mendonça

2. 1. INTRODUÇÃO
Elevando-se a temperatura de um corpo, geralmente, suas
dimensões aumentam devido ao aumento da distância média
entre as partículas que o constituem. Este fenômeno é chamado
de dilatação térmica.
DILATAÇÃO

3. OBS: DIMINUINDO-SE A TEMPERATURA OCORRE
A CONTRAÇÃO TÉRMICA.
Os fios elétricos entre os postes
nas ruas e entre as torres das
linhas de alta tensão, ao serem
instalados, não são esticados.
Esse procedimento visa a evitar
que, no inverno, com a queda de
temperatura, a contração térmica
possa esticar esses fios a ponto
de se romperem.

4. DILATAÇÃO LINEAR(Δℓ): É O ACRÉSCIMO DE COMPRIMENTO
QUANDO ELEVA-SE A TEMPERATURA DE UM CORPO.
ΔT→ variação de temperatura.
: ℓo → comprimento inicial.
α(alfa) → coeficiente de dilatação linear (depende da temperatura e do
material que constitui o corpo ).

5. JUNTA DE DILATAÇÃO → É O ESPAÇO DEIXADO
ENTRE OS SEGMENTOS DE UMA CONSTRUÇÃO PARA PERMITIR A LIVRE
DILATAÇÃO DO MATERIAL, DEVIDO AO AUMENTO DE TEMPERATURA.
As ferrovias, pontes, viadutos e
grandes construções são feitos
em segmentos, com um
espaço entre eles (junta de
dilatação) para permitir a livre
dilatação do material
quando a temperatura aumentar.
Assim, os trilhos da ferrovia não
entortam e o concreto das
construções não racha.

6. DILATAÇÃO SUPERFICIAL (ΔA) → É O ACRÉSCIMO DE
ÁREA
QUANDO ELEVA-SE A TEMPERATURA DE UM CORPO .

8. OBS: ELEVANDO-SE A TEMPERATURA DE UMA CHAPA COM ORIFÍCIO, O
ORIFÍCIO SE DILATA JUNTAMENTE COM A CHAPA, POIS ELE SE COMPORTA
COMO SE FOSSE CONSTITUÍDO DO MESMO MATERIAL DA CHAPA.

9. DILATAÇÃO VOLUMÉTRICA OU CÚBICA(ΔV): É O
ACRÉSCIMO DE VOLUME QUANDO ELEVA–SE A TEMPERATURA DE
UM
CORPO.

10. LAMINAS BIMETÁLICAS
Utilizadas em
ferroelétricos

11. DILATAÇÃO ANÔMALA

13. EXERCÍCIO
• O gráfico abaixo representa a variação do comprimento de uma barra homogênea com a
temperatura. Determine o coeficiente de dilatação linear de que a barra é constituída.

14. SOLUÇÃO

15. EXERCÍCIO
• A extensão de trilhos de ferro sofre dilatação linear, calcule o aumento de comprimento que
1000 m dessa ferrovia sofre ao passar de 0 °C para 20 °C, sabendo que o coeficiente de
dilatação linear do ferro é 12.10-6 °C-1.

16. SOLUÇÃO
• Obs: Aumento de comprimento sempre indica variação, ou seja, ∆L.
• ∆L = Lo α ∆T (o primeiro passo é substituir os valores dados na equação)
∆L = 1000. 12.10-6 .20
∆L = 20 000. 12.10-6 (nesse momento foi multiplicado os termos inteiros para
depois trabalharmos com o expoente de base 10).
∆L = 24.10-2 (transformação de notação científica para forma decimal).
∆L = 0,24 m

17. EXERCÍCIO
• (VUNESP-SP) A dilatação térmica dos sólidos é um fenômeno importante em diversas
aplicações de engenharia, como construções de pontes, prédios e estradas de ferro.
Considere o caso dos trilhos de trem serem de aço, cujo coeficiente de dilatação é α = 11 .
10-6
°C-1
. Se a 10°C o comprimento de um trilho é de 30m, de quanto aumentaria o seu
comprimento se a temperatura aumentasse para 40°C?
a) 11 . 10-4
m
b) 33 . 10-4
m
c) 99 . 10-4
m
d) 132 . 10-4
m
e) 165 . 10-4
m

18. SOLUÇÃO
• O cálculo da dilatação linear ΔL, do trilho é:
ΔL = L0 . α . Δθ
ΔL = 30 . (11 . 10-6
) . (40 – 10) = 99 . 10-4
m
RESPOSTA: C

19. EXERCÍCIO
• (Fatec) Um bloco maciço de zinco tem forma de cubo, com aresta de 20cm a 50°C. O
coeficiente de dilatação linear médio do zinco é 25.10-6
°C-1
.
• O valor, em cm², que mais se aproxima do volume desse cubo a uma temperatura de -50°C
é:

20. SOLUÇÃO
• Este é um exercício típico de dilatação volumétrica onde se da o coeficiente de dilatação linear
(CUIDADO).
• Sabemos que o coeficiente de dilatação volumétrica é 3 vezes o de dilatação linear , então
• ΔV = V0 x γ x Δt
• Que é mesma coisa que
• ΔV = V0 x 3α x Δt
• V – V0= V0 x 3α x Δt
• Como o volume do cubo é a aresta ao cubo temos!
• V – 20³ = 20³ x 3(25.10-6
) (-50-50)
• V – 20³ = -60
• V = -60 + 8000
• V = 7940cm³

21. EXERCÍCIO DESAFIO
• (UFRS-RS) Assinale a alternativa que preenche corretamente as lacunas do texto a seguir,
na ordem em que aparecem.
• A figura que segue representa um anel de alumínio homogêneo, de raio interno Ra e raio
externo Rb, que se encontra à temperatura ambiente.
• Se o anel for aquecido até a temperatura de 200 °C, o raio Ra .......... e o raio Rb .......... .
• a) aumentará - aumentará
• b) aumentará - permanecerá constante
• c) permanecerá constante - aumentará
• d) diminuirá - aumentará
• e) diminuirá - permanecerá constante

22. Obrigada !!!