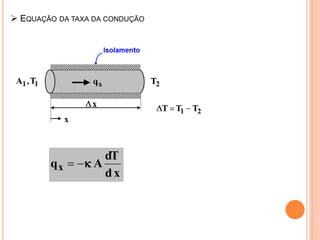
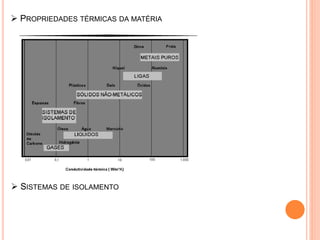
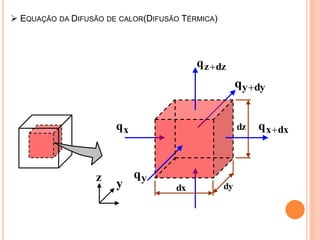
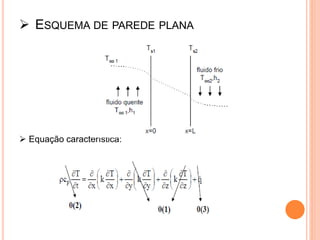
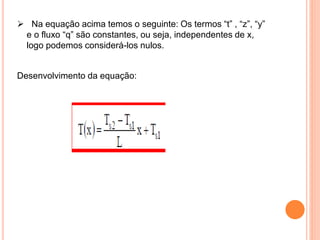
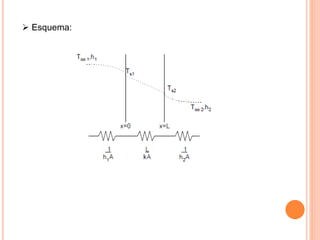
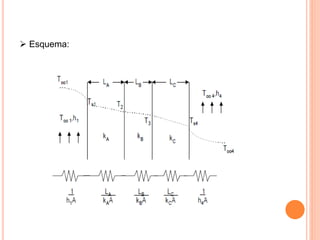
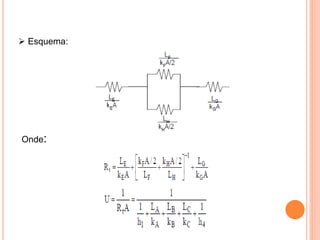
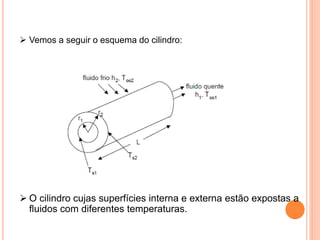
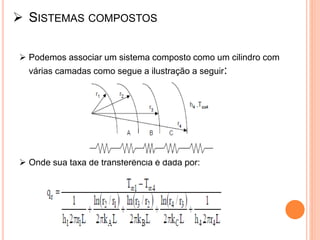
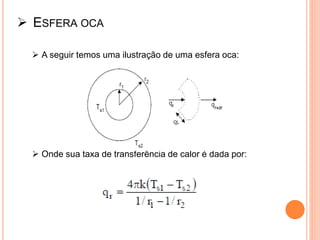
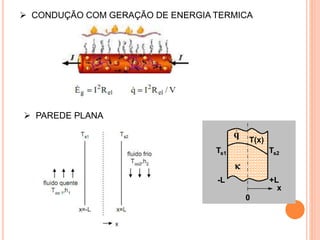
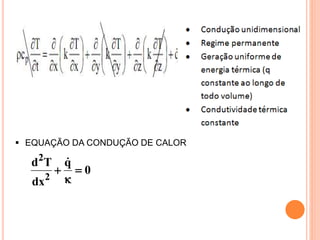
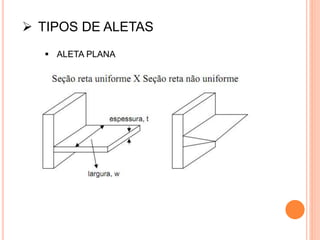
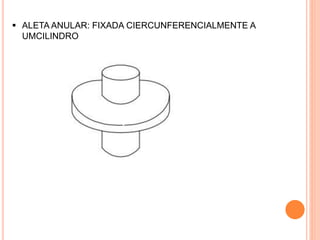
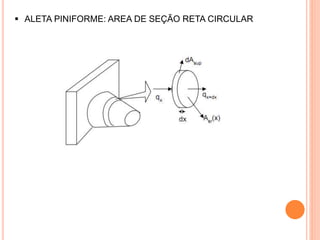
O documento apresenta uma introdução sobre transferência de calor, abordando os três modos de transferência: condução, convecção e radiação. Foca especificamente na condução de calor, explicando suas origens físicas e equações que descrevem a taxa de transferência de calor. Também discute a relação com a termodinâmica e a relevância do tópico para engenharia.

1. CONDUÇÃO DE CALOR
Disciplina : Fenômenos de transporte
Prof: Emanuel Almeida
Grupo: Alex Ferreira
Deivison Lima
Willian Renos,
Victor Ramon
Curso: Bacharelado em Engenharia Elétrica

2. INTRODUÇÃO A TRANSFERÊNCIA DE CALOR
 INTRODUÇÃO
 O QUE E COMO?
 CONDUÇÃO
 CONVECÇÃO
 RADIAÇÃO
 ORIGENS FÍSICAS E EQUAÇÕES DE TAXA DE TRANSFERÊNCIA DE CALOR
 RELAÇÃO COM A TERMODINÂMICA
 A EXIGÊNCIA DA CONSERVAÇÃO DA ENERGIA
 RELEVÂNCIA DA TRANSFERÊNCIA DE CALOR

3.  INTRODUÇÃO
 TERMODINÂMICA: INTERAÇÕES CHAMADAS CALOR E TRABALHO;
 TERMODINÂMICA: LIDA APENAS COM EXTREMOS DO PROCESSO;
 OBJETIVO: É MOSTRAR A ANÁLISE TERMODINÂMICA ATRAVÉS DOS
ESTUDOS DOS MODOS DE TRANSFERÊNCIA DE CALOR DANDO ÊNFASE AO
MODO DE TRANSFERÊNCIA CONHECIDO COMO CONDUÇÃO.
 O QUE E COMO?
 O QUE É TRANSFERÊNCIA DE CALOR?
TRANSFERÊNCIA DE CALOR É ENERGIA TÉRMICA EM TRÂNSITO DEVIDO A
DIFERENÇA DE TEMPERATURA NO ESPAÇO.

4.  O QUE É TRANSFERÊNCIA DE CALOR POR CONDUÇÃO?
 O QUE É TRANSFERÊNCIA DE CALOR POR CONVECÇÃO?
 O QUE E COMO?
OCORRE QUANDO EXISTE UM GRADIENTE DE TEMPERATURA EM UM MEIO
ESTACIONÁRIO QUE PODE SER UM SÓLIDO OU UM FLUIDO.
OCORRERÁ ENTRE UMA SUPERFÍCIE E UM FLUIDO EM MOVIMENTO
QUANDO ELES ESTIVEREM A DIFERENTES TEMPERATURAS.

5.  O QUE E COMO?
 O QUE É TRANSFERÊNCIA DE CALOR POR CONVECÇÃO?
OCORRE PORQUE TODAS AS SUPERFÍCIES COM TEMPERATURAS NÃO
NULA EMITEM ENERGIA NA FORMA DE ONDAS ELETROMAGNÉTICAS.

6.  ORIGENS FÍSICAS E EQUAÇÕES DE TAXA DE TRANSFERÊNCIA DE CALOR
A condução pode ser vista como a transferência de energia das
partículas mais energéticas para as menos energéticas de uma
substância devido às interações entre partículas.
dx
dT
kqx ''
''
xq é o fluxo térmico e representa a taxa de transferência de
calor na direção x
dxdT / é o gradiente de temperatura
k é a condutividade e depende do material

7. L
TT
dx
dT 12 

L
TT
kqx
12'' 

L
T
k
L
TT
kqx



 12''
 ORIGENS FÍSICAS E EQUAÇÕES DE TAXA DE TRANSFERÊNCIA DE CALOR
Nas condições de estado estacionário, com a distribuição linear, o
gradiente de temperatura pode ser representado como:
e o fluxo térmico é, então,
ou

8. A taxa de transferência de calor por condução, qx (W), através de uma
parede plana com área A, é, então, o produto do fluxo e da área.
 ORIGENS FÍSICAS E EQUAÇÕES DE TAXA DE TRANSFERÊNCIA DE CALOR
Aqq xx  ''
Independentemente da natureza específica do processo de
transferência de calor por convecção, a equação apropriada para a
taxa de transferência possui a forma
)(''
 TThq s
é o fluxo de calor por convecção
''
q
TTs , São as temperaturas da superfície e do fluido, respectivamente
h é o coeficiente de transferência de calor por convecção

9.  RELAÇÃO COM A TERMODINÂMICA
É apropriado observar as diferenças fundamentais entre a transferência
de calor e a termodinâmica. Embora a termodinâmica esteja votada
para as interações envolvendo calor e para o importante papel que elas
desempenham na primeira e segunda leis, ela não considera nem os
mecanismos que viabilizam a transferência de calor nem os métodos
que existem para calcular a taxa de troca de calor.
Por outro lado, transferência de calor procura fazer o que a
termodinâmica é inerentemente incapaz, ou seja, quantificar a taxa de
transferência de calor que ocorre em termos do grau de não-equilíbrio
térmico, uma vez que a transferência de calor é por essência um
processo de não-equilíbrio.

10.  A EXIGÊNCIA DA CONSERVAÇÃO DA ENERGIA
WQEtot
acu  PRIMEIRA LEI DA TERMODINÂMICA
tot
acuE É A VARIAÇÃO DA ENERGIA TOTAL ACUMULADA
Q é o valor líquido do calor transferido
W é o valor líquido do trabalho efetuado

11.  RELEVÂNCIA DA TRANSFERÊNCIA DE CALOR
A transferência de calor é um aspecto dominante em praticamente todos
os dispositivos de conservação e produção de energia.
Ela não é importante somente em sistemas de engenharia, mas
também na natureza.
Então, ter conhecimento a respeito de tal área é acrescentar ainda
mais conteúdo a nossa formação como profissionais de engenharia.

12. Exemplo 1.
A parede de um forno industrial é constituída em tijolo refratário com
0,15m de espessura, cuja condutividade térmica é de 1,7W/(m.K).
Medidas efetuadas ao longo da operação em regime estacionário revelam
temperaturas de 1400 e 1150K nas paredes internas e externa,
respectivamente. Qual é a taxa de calor perdida através de uma parede
que mede 0,5m por 1,2m?
Solução:
2
''
2833
15,0
250
7,1
m
W
L
T
kqx 



13.  EQUAÇÃO DA TAXA DA CONDUÇÃO
xd
dT
Aqx 

14.  PROPRIEDADES TÉRMICAS DA MATÉRIA
 SISTEMAS DE ISOLAMENTO

15.  EXERCÍCIO DE FIXAÇÃO
A difusividade termica "alfa" é a propriedade de transporte que controla
um processo de transferencia de calor por conduçao em regime
transiente. Usando os valores apropriados de k, rô e Cp abaixo, calcule
"alfa" para os seguintes materiais nas temperaturas indicadas: aluminio
puro, 300 e 700 K; carbeto de silicio, 1000 K; parafina, 300 K.

16.  EQUAÇÃO DA DIFUSÃO DE CALOR(DIFUSÃO TÉRMICA)
Um dos objetivos da equação é determinar o campo de temperaturas,
ou seja, queremos conhecer as distribuições de temperaturas que vão
dizer como ela vai se comportar em cada posição no meio. Sabendo-se
desse comportamento, o fluxo de calor por condução em qualquer ponto
do meio ou na superfície pode ser determinado através da lei de
Fourier. A distribuição de temperaturas pode ser usada para otimizar
espessuras de um material isolante.

17.  EQUAÇÃO DA DIFUSÃO DE CALOR(DIFUSÃO TÉRMICA)
As taxas de transferência de calor representada em serie de Taylor:
...
!2
dx
x
q
dx
x
q
qq
2
2
x
2
x
xdxx 






...
!2
dy
y
q
dy
y
q
qq
2
2
y
2
y
ydyy 






...
!2
dz
z
q
dz
z
q
qq
2
2
z
2
z
zdzz 







18.  EQUAÇÃO DA DIFUSÃO DE CALOR(DIFUSÃO TÉRMICA)
Taxa de geração de energia térmica(W/m³) no interior do meio:
dzdydxqEg
 
Taxa de variação da energia(kW) acumulada pela materia:
dzdydx
t
T
cE pacu


 
Forma geral da exigência da conservação da energia:
entra sai g acuE E E E  

19.  EQUAÇÃO DA DIFUSÃO DE CALOR(DIFUSÃO TÉRMICA)
y
z
xq
yq
dxxq 
dyyq 
dzzq 
dz
dx dy

20.  EQUAÇÃO DA DIFUSÃO DE CALOR(DIFUSÃO TÉRMICA)
Substituindo as equações temos:
t
T
cq
z
T
zy
T
yx
T
x
p
































 
OBS: Para um regime estacionário, não pode haver variação na
quantidade da energia armazenada.

21.  EXERCÍCIO DE FIXAÇÃO
A distribuição de temperatura através de uma parede de 1m de
espessura num dado instante de tempo é dada por:
T(x) = a + b.x + c.x2
em que T está em graus Celsius e x em metros, enquanto a = 900 ºC, b
= -300ºC/m e c = -50ºC/m2. A parede gera um calor uniforme igual a
1000 W/m3, e sua área é de 10 m2, com as seguintes propriedades:
massa específica = 1600 kg/m3, K = 40 W/m.K e cp = 4 kJ/kg.K.
a) Determine a taxa de transferência de calor que entra na parede
(x = 0) e a que sai (x = 1m).
b) Determine a taxa de variação da energia armazenada na parede.
c) Determinar a taxa de variação da temperatura em relação ao tempo
nas posições x=0; 0,25 e 0,5.

22. CONDUÇÃO UNIDIMENSIONAL EM REGIME
ESTACIONÁRIO
 Entende-se por condução unidimensional ao fato de que
apenas uma coordenada é necessária para descrever a
variação espacial das variáveis dependentes.
 Logo neste caso podemos considerar que a transferência
de calor se dá em uma única direção, que no caso é o eixo
“x”.

23.  PAREDE PLANA
 Observamos que na condução de calor em uma única
direção que se dá em uma parede plana, a temperatura é
uma função somente da coordenada x e o calor é transferida
somente nessa direção. De uma forma geral o calor é
transferido do meio mais energético (quente) para o menos
energético (frio).

24.  ESQUEMA DE PAREDE PLANA
 Equação característica:

25.  Na equação acima temos o seguinte: Os termos “t” , “z”, “y”
e o fluxo “q” são constantes, ou seja, independentes de x,
logo podemos considerá-los nulos.
Desenvolvimento da equação:

26.  O significado matemático da equação acima é que a variação da
temperatura em uma parede plana é linear.
Onde:
O fluxo independe de x.

27.  RESISTÊNCIA TÉRMICA
 Podemos fazer uma analogia entre resistência térmica e
resistência térmica, ou seja, a resistência térmica está
associada a facilidade ou dificuldade da condução do calor.

28.  Esquema:

29.  RESISTÊNCIA TÉRMICA
 Sua equação característica é:
Para a condução:
Para convecção :

30.  Da mesma forma que em um circuito elétrico, um sistema de calor
pode ser decomposto para facilitar seu entendimento e sua taxa de
transferência de calor pode ser calculada através da seguinte
equação:

31.  PAREDE COMPOSTA
 Paredes compostas também podem ser consideradas como
sistemas de calor, dividindo-se cada camada como uma
resistência térmica em série e em paralelo pelo fato de
existirem vários diferentes materiais.
 Diferente da parede plana não-composta, a transferência de
calor é multidimensional, mas , geralmente consideramos a
hipótese de um sistema unidimensional e prosseguir com a
análise do circuito.

32.  Esquema:

33.  Em sistemas compostos, é comumente o trabalho com o uso
de um coeficiente global de transferência de calor.
 Como citamos anteriormente a transferência de calor
pode ser considerada unidimensional, aproximando pelo
seguinte circuito:

34.  Esquema:
Onde:

35.  RESISTÊNCIA DE CONTATO
 É importante considerarmos que em sistemas compostos a
queda de temperatura entre as interfaces dos vários materiais
pode ser considerável. Essa mudança se deve à resistência
térmica de contato.
 Alguns fatores podem contribuir para o aumento ou a
diminuição de tal resistência como a rugosidade, área dos
pontos de contato, uso de graxas térmicas, enchimentos,etc.

36.  A seguir, temos um exemplo:

37.  Considerações feitas no exemplo:

38.  SISTEMAS RADIAIS
 Na análise dos sistemas radiais, cilíndricos e esféricos existe
gradiente de temperatura somente na direção radial, o que
possibilita visualizarmos como sistemas unidimensionais.

39.  Vemos a seguir o esquema do cilindro:
 O cilindro cujas superfícies interna e externa estão expostas a
fluidos com diferentes temperaturas.

40.  E sua equação característica:
 Após integrar a expressão temos:

41.  E sua taxa de transferência é considerada constante na
direção radial.
 Da mesma forma que analisamos anteriormente um sistema
unidimensional, procedemos da mesma maneira para um
sistema radial.

42.  A seguir temos a solução geral:
 Onde concluímos que a distribuição de temperatura associada à
condução radial através de uma parece cilíndrica é logarítmica, não
linear.
 Também consideramos a resistência térmica neste meio como:

43.  SISTEMAS COMPOSTOS
 Podemos associar um sistema composto como um cilindro com
várias camadas como segue a ilustração a seguir:
 Onde sua taxa de transferência é dada por:

44.  ESFERA OCA
 A seguir temos uma ilustração de uma esfera oca:
 Onde sua taxa de transferência de calor é dada por:

45.  A sua resistência térmica é dada por:

46.  CONDUÇÃO COM GERAÇÃO DE ENERGIA TERMICA
 PAREDE PLANA
Ts1 Ts2
+L
q
-L
x
T(x)

0

47. 2
2
d T q
0
dx
 

 EQUAÇÃO DA CONDUÇÃO DE CALOR

48.  DISTRIBUIÇÃO DE TEMPERATURA
SISTEMAS RADIAIS
 DISTRIBUIÇÃO DE TEMPERATURA

49. TRANFERENCIA DE CALOR EM SUPERFICIE
ESTENDIDAS
 O termo superfície estendida é comumente usado para
descrever um caso especial importante envolvendo a
transferência de calor por condução n interior de um solido e
a transferência de calor por convecção nas fronteiras do
solido.
 ALETAS
 Uma superfície estendida usada especificamente para
aumentar a taxa de transferência de calor entre um solido e
um fluido adjacente.

50.  TIPOS DE ALETAS
 ALETA PLANA

51.  ALETA ANULAR: FIXADA CIERCUNFERENCIALMENTE A
UMCILINDRO

52.  ALETA PINIFORME: AREA DE SEÇÃO RETA CIRCULAR

54. a) Calcular a resistência térmica
resp.=
b) Calcular a perda total de calor
resp.=