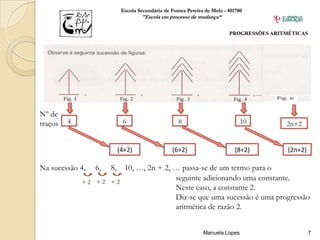
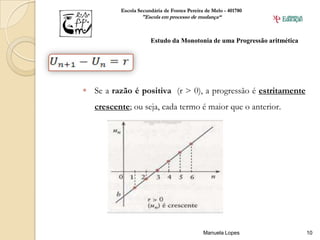
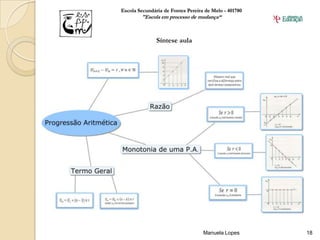
A aula abordou progressões aritméticas, definindo-as, estudando a monotonia, calculando termos gerais e resolvendo exercícios. Os alunos praticaram os conceitos e a professora apresentou a fórmula para calcular a soma dos primeiros termos de uma progressão aritmética.