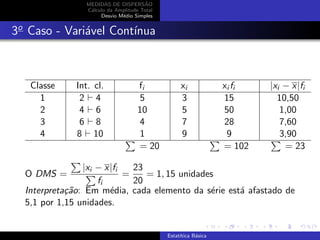
MEDIDAS DE DISPERSÃO introduz medidas de dispersão absoluta como amplitude total e desvio médio simples. A amplitude total é a diferença entre o maior e menor valor da série. O desvio médio simples é a média aritmética dos desvios de cada elemento em relação à média da série. O documento explica o cálculo destas medidas para variáveis discretas e contínuas.

1. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Prof. Me. Josivaldo Nascimento dos Passos
MEDIDAS DE DISPERS˜AO
UNIVERSIADE ESTADUAL DO MARANH˜AO
17 de outubro de 2016
Estat´ıtica B´asica

2. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Sum´ario
MEDIDAS DE DISPERS˜AO
Introdu¸c˜ao;
Medidas de Dispers˜ao Absoluta;
Amplitude Total;
C´alculo da Amplitude Total;
Desvio M´edio Simples;
C´alculo do Desvio M´edio Simples:
1o Caso - DADOS BRUTOS OU ROL
2o Caso - Vari´avel Discreta
3o Caso - Vari´avel Cont´ınua
Estat´ıtica B´asica

3. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Introdu¸c˜ao
Uma breve reflex˜ao sobre as medidas de tendˆencia central permite-
nos concluir que elas n˜ao s˜ao suficientes para caracterizar totalmente
uma sequˆencia num´erica.
Se observarmos as sequˆencias:
X : 10, 1, 18, 20, 35, 3, 7, 15, 11, 10
Y : 12, 13, 13, 14, 12, 14, 12, 14, 13, 13
Z : 13, 13, 13, 13, 13, 13, 13, 13, 13, 13
concluiremos que todas possuem a mesma m´edia 13.
No entanto, s˜ao sequˆencias completamente distintas do ponto de
vista da variabilidade de dados.
Estat´ıtica B´asica

4. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Introdu¸c˜ao
Na sequˆencia Z (3) n˜ao h´a variabilidade de dados.
A m´edia 13 representa bem qualquer valor da s´erie.
Na sequˆencia Y , a m´edia 13 representa bem a s´erie, mas existem
elementos da s´erie levemente diferenciados da m´edia 13.
Na sequˆencia X existem muitos elementos bastante diferenciados da
m´edia 13.
Conclu´ımos que a m´edia 13 representa otimamente a sequˆencia Z,
representa bem a sequˆencia Y , mas n˜ao representa bem a sequˆencia
X.
Estat´ıtica B´asica

5. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Conceitos
O nosso objetivo ´e construir medidas que avaliem a representativi-
dade da m´edia. Para isto usaremos as medidas de dispers˜ao.
Observe que na sequˆencia Z os dados est˜ao totalmente concentrados
sobre a m´edia 13.
N˜ao h´a dispers˜ao de dados. Na sequˆencia Y h´a forte concentra¸c˜ao
dos dados sobre a m´edia 13, mas h´a fraca dispers˜ao de dados. J´a
na s´erie X h´a fraca concentra¸c˜ao de dados em torno da m´edia 13 e
forte dispers˜ao de dados em rela¸c˜ao a m´edia 13.
Estat´ıtica B´asica

6. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Medidas de Dispers˜ao Absoluta
As principais medidas de dispers˜ao absolutas s˜ao: amplitude total,
desvio m´edio simples, variˆancia e desvio padr˜ao.
Amplitude Total - ´E a diferen¸ca entre o maior e o menor valor da
sequˆencia.
Estat´ıtica B´asica

7. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
1o
Caso - DADOS BRUTOS OU ROL
Basta identificar o maior e o menor valor da sequˆencia e efetuar a
diferen¸ca entre estes valores.
Exemplo
Determine a amplitude total da sequˆencia X : 11, 12, 9, 10, 10, 15.
O maior valor desta sequˆencia ´e 15 e o menor valor ´e 9. Portanto,
a amplitude total da sequˆencia ´e At = 15 − 9 = 6 unidades.
Estat´ıtica B´asica

8. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
2o
Caso - VARI´AVEL DISCRETA
Como os valores j´a se apresentam ordenados, a amplitude total ´e a
diferen¸ca entre o ´ultimo e o primeiro elemento da s´erie.
Exemplo
Determine a amplitude total da s´erie.
xi fi
2 1
3 6
5 10
7 3
O maior valor da s´erie ´e 7 e o menor valor da s´erie ´e 2. Portanto, a
amplitude total da s´erie ´e At = 7 − 2 = 5 unidades.
Estat´ıtica B´asica

9. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - VARI´AVEL CONT´INUA
Nesta situa¸c˜ao, por desconhecer o maior e o menor valor da s´erie
devemos fazer um c´alculo aproximado da amplitude total da s´erie.
Consideraremos como maior valor da s´erie o ponto m´edio da ´ultima
classe e como menor valor da s´erie o ponto m´edio da primeira classe.
A amplitude total ´e a diferen¸ca entre estes valores.
Exemplo
Determine a amplitude total da s´erie:
Classe Int. cl. fi
1 2 4 5
2 4 6 10
3 6 8 20
4 8 10 7
5 10 12 2
Estat´ıtica B´asica

10. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - VARI´AVEL CONT´INUA
O ponto m´edio da ´ultima classe ´e 11 e o ponto m´edio da primeira
classe ´e 3. Portanto, At = 11 − 3 = 8 unidades.
COMENT´ARIO: Apesar da facilidade de obten¸c˜ao da amplitude
total, esta medida apresenta a inconveniˆencia de depender apenas
de dois valores da s´erie. ´E poss´ıvel modificar completamente a dis-
pers˜ao ou a concentra¸c˜ao dos elementos em torno da m´edia, sem
alterar a amplitude total da s´erie. ´E uma medida que tem pouca
sensibilidade estat´ıstica.
Estat´ıtica B´asica

11. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
Desvio M´edio Simples
O conceito estat´ıstico de desvio corresponde ao conceito matem´atico
de distˆancia.
A dispers˜ao dos dados em rela¸c˜ao a m´edia de uma sequˆencia pode
ser avaliada atrav´es dos desvios de cada elemento da sequˆencia em
rela¸c˜ao a m´edia da sequˆencia.
O desvio m´edio simples que indicaremos por DMS ´e definido como
sendo uma m´edia aritm´etica dos desvios de cada elemento da s´erie
para a m´edia da s´erie
Estat´ıtica B´asica

12. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
1o
Caso - DADOS BRUTOS OU ROL
Calculamos inicialmente a m´edia da sequˆencia. Em seguida identi-
ficamos a distˆancia de cada elemento da sequˆencia para sua m´edia.
Finalmente, calculamos a m´edia destas distˆancias.
Se a sequˆencia for representada por X : x1, x2, . . . , xn, ent˜ao o DMS
admite como f´ormula de c´alculo:
DMS =
|xi − x|
n
Exemplo
Calcule o DMS para a sequˆencia: X : 2, 8, 5, 6.
Estat´ıtica B´asica

13. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
1o
Caso - DADOS BRUTOS OU ROL
Determinamos inicialmente a m´edia da s´erie:
X =
xi
n
=
2 + 8 + 5 + 6
4
= 5, 25
em seguida determinamos as distˆancias de cada elemento da s´erie
para a m´edia da s´erie:
|x1 − x| = |2 − 5, 25| = 3, 25
|x1 − x| = |8 − 5, 25| = 2, 75
|x1 − x| = |5 − 5, 25| = 0, 25
|x1 − x| = |6 − 5, 25| = 0, 75
O DMS ´e a m´edia aritm´etica simples destes valores.
DMS =
3, 25 + 2, 75 + 0, 25 + 0, 75
4
=
7
4
= 1, 75
Interpreta¸c˜ao: Em m´edia, cada elemento da sequˆencia est´a afastado
do valor 5,25 por 1,75 unidades.
Estat´ıtica B´asica

14. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
2o
Caso - Vari´avel Discreta
No caso da apresenta¸c˜ao de uma vari´avel discreta, lembramos que a
frequˆencia simples de cada elemento representa o n´umero de vezes
que este valor figura na s´erie. Conseq¨uentemente, haver´a repeti¸c˜oes
de distˆancias iguais de cada elemento distinto da s´erie para a m´edia
da s´erie. Assim, a m´edia indicada para estas distˆancias ´e uma m´edia
aritm´etica ponderada.
A f´ormula para o c´alculo do DMS ´e:
DMS =
|xi − x|fi
fi
Estat´ıtica B´asica

15. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
2o
Caso - Vari´avel Discreta
Exemplo
Determine o DMS para a s´erie:
xi fi
1 2
3 5
4 2
5 1
O n´umero de elementos da s´erie ´e n = fi = 10.
A m´edia da s´erie ´e:
X =
xi fi
fi
Usaremos a disposi¸c˜ao da tabela, acrescentando novas colunas para
a resolu¸c˜ao dos c´alculos.
Estat´ıtica B´asica

16. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
2o
Caso - Vari´avel Discreta
xi fi xi fi
1 2 2
3 5 15
4 2 8
5 1 5
fi = 10 xi fi = 30
A m´edia da s´erie ´e:
X =
xi fi
fi
=
30
10
= 3
O DMS ´e dado por:
DMS =
|xi − x|fi
fi
Estat´ıtica B´asica

17. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
2o
Caso - Vari´avel Discreta
Incluiremos outra coluna para efetuar estes c´alculos:
xi fi xi fi |xi − x|fi
1 2 2 4
3 5 15 0
4 2 8 2
5 1 5 2
fi = 10 xi fi = 30 |xi − x|fi = 8
O desvio m´edio simples ´e:
DMS =
|xi − x|fi
fi
=
8
10
= 0, 8 unidades.
Interpreta¸c˜ao: Em m´edia, cada elemento da s´erie est´a afastado do
valor 3 por 0,8 unidade.
Estat´ıtica B´asica

18. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - Vari´avel Cont´ınua
Nesta situa¸c˜ao, por desconhecer os valores individuais dos elementos
componentes da s´erie, substituiremos estes valores xi , pelos pontos
m´edios de classe.
Desta forma, o desvio m´edio simples tem por c´alculo a f´ormula:
DMS =
|xi − x|fi
fi
onde xi ´e o ponto m´edio da classe i.
Estat´ıtica B´asica

19. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - Vari´avel Cont´ınua
Exemplo
Determine o DMS para a s´erie.
Classe Int. cl. fi
1 2 4 5
2 4 6 10
3 6 8 4
4 8 10 1
O n´umero de elementos da s´erie ´e n = fi = 20. Usaremos a
disposi¸c˜ao da tabela acrescentando as colunas necess´arias para a
resolu¸c˜ao dos c´alculos.
Estat´ıtica B´asica

20. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - Vari´avel Cont´ınua
Inicialmente acrescentamos a coluna dos pontos m´edios das classes:
Classe Int. cl. fi xi
1 2 4 5 3
2 4 6 10 5
3 6 8 4 7
4 8 10 1 9
fi = 20
Em seguida, calculamos a m´edia da s´erie: X =
xi fi
fi
Estat´ıtica B´asica

21. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - Vari´avel Cont´ınua
Classe Int. cl. fi xi xi fi
1 2 4 5 3 15
2 4 6 10 5 50
3 6 8 4 7 28
4 8 10 1 9 9
fi = 20 xi fi = 102
A m´edia da s´erie ´e:
X =
xi fi
fi
=
102
20
= 5, 1
O DMS ´e dado por DMS =
|xi − x|fi
fi
Estat´ıtica B´asica

22. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - Vari´avel Cont´ınua
Classe Int. cl. fi xi xi fi |xi − x|fi
1 2 4 5 3 15 10,50
2 4 6 10 5 50 1,00
3 6 8 4 7 28 7,60
4 8 10 1 9 9 3,90
= 20 = 102 = 23
O DMS =
|xi − x|fi
fi
=
23
20
= 1, 15 unidades
Interpreta¸c˜ao: Em m´edia, cada elemento da s´erie est´a afastado de
5,1 por 1,15 unidades.
Estat´ıtica B´asica

23. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
3o
Caso - Vari´avel Cont´ınua
COMENT´ARIO: O desvio m´edio simples depende de cada compo-
nerte da s´erie. Se mudarmos o valor de um ´unico elemento da s´erie,
mudamos tamb´em o DMS. Portanto, o desvio m´edio simples tem
perfeita sensibilidade estat´ıstica. A maior dificuldade desta medida
´e envolver m´odulos, cujas propriedades, em geral n˜ao s˜ao suficien-
temente conhecidas pelos estagi´arios que normalmente desenvolvem
estes c´alculos.
Estat´ıtica B´asica

24. MEDIDAS DE DISPERS˜AO
C´alculo da Amplitude Total
Desvio M´edio Simples
MARTINS, Gilberto de Andrade Martins, Estat´ıstica Geral e
Aplicada, 4 ed. S˜ao Paulo: Editora Atlas S.A., 2011
SILVA, Ermes Medeiros da; SILVA, Elio Medeiros da;
GONC¸ALVES, Valter; MUROLO, Afrˆanio Carlos,
ESTAT´ISTICA Para os cursos de: Economia, Administra¸c˜ao e
Ciˆencias Contabeis 3 ed. S˜ao Paulo: Editora Atlas S.A., 1999
Estat´ıtica B´asica