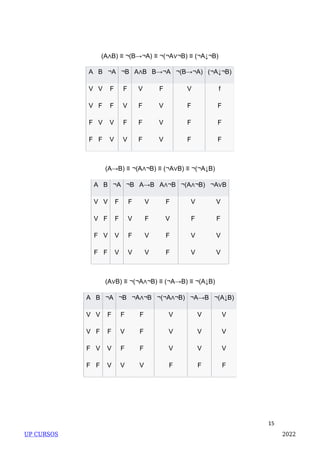
O documento discute os três tipos de raciocínio lógico - dedução, indução e abdução - e fornece exemplos de cada um. Também explica lógicas argumentativas como proposições, negação, conjunção, disjunção, condicional e bicondicional. Por fim, aborda operações lógicas, arranjos simples, combinações simples e tabela verdade.

1. UP CURSOS 2022

2. Robótica na Educação
UP CURSOS 2022

3. 1
Os três tipos de raciocínio lógico: dedução, indução e abdução ........................ 2
Lógicas argumentativas: Preposições, negação, conjunção, disjunção,
condicional, bicondicional...................................................................................5
Operações lógicas............................................................................................. 8
Arranjos simples.............................................................................................. 10
Combinações simples ......................................................................................11
Tabela verdade ................................................................................................13
Propriedades....................................................................................................16
Análise combinatória ........................................................................................ 19
A regra de três................................................................................................. 21
Referências bibliográficas ................................................................................25
UP CURSOS 2022

4. 2
OS TRÊS TIPOS DE RACIOCÍNIO LÓGICO:
DEDUÇÃO, INDUÇÃO E ABDUÇÃO
Em lógica, pode-se distinguir três tipos de raciocínio lógico: dedução, indução e
abdução. Dada uma premissa, uma conclusão, e uma regra segundo a qual
a premissa implica a conclusão, eles podem ser explicados da seguinte forma:
Dedução
Corresponde a determinar a conclusão. Utiliza-se a regra e a sua premissa
para chegar a uma conclusão, por exemplo: "Quando chove, a relva fica
molhada. Hoje choveu, portanto a relva está molhada." É comum associar-se
os matemáticos a este tipo de raciocínio.
Método dedutivo é a modalidade de raciocínio lógico que faz uso da dedução
para obter uma conclusão a respeito de determinadas premissas. O método
dedutivo normalmente se contrasta com o Método indutivo
Essencialmente, os raciocínios dedutivos se caracterizam por apresentar
conclusões que devem, necessariamente, ser verdadeiras caso todas as
premissas sejam verdadeiras e se o raciocínio respeitar uma forma lógica
válida.
Partindo de princípios reconhecidos como verdadeiros (premissa maior), o
pesquisador estabelece relações com uma segunda proposição (premissa
menor) para, a partir de raciocínio lógico, chegar à verdade daquilo que propõe
(conclusão).
Uma dedução é uma espécie de argumento no qual a forma lógica válida
garante a verdade da conclusão se as premissas forem verdadeiras. Por
exemplo: Temos duas premissas verdadeiras:
"P1: Todos os homens são mortais."
"P2: Sócrates é homem."
UP CURSOS 2022

5. 3
Agora apresentemos uma forma lógica válida:
"TODO x é y.
z é x.
Logo, z é y"
Veja que as duas premissas obedecem a uma forma lógica válida. Se a
conclusão for "Logo, Sócrates é mortal (Logo, z é y)", então temos uma
dedução.
Indução
É determinar a regra. É aprender a regra a partir de diversos exemplos de
como a conclusão segue da premissa. Exemplo: "A relva ficou molhada em
todas as vezes que choveu. Então, se chover amanhã, a relva ficará molhada."
É comum associar os cientistas a este estilo de raciocínio.
Na lógica, método indutivo ou indução é o raciocínio que, após considerar um
número suficiente de casos particulares, conclui uma verdade geral. A indução,
ao contrário da dedução, parte de dados particulares da experiência sensível.
De acordo com o indutivista, a ciência começa com a observação. A
observação, por sua vez, fornece uma base segura sobre a qual o
conhecimento científico pode ser construído, e o conhecimento científico é
obtido a partir de proposições de observação por indução. Afirmações a
respeito da construção do conhecimento rigorosas como esta sofrem de
dificuldades quanto a sua validade, como demonstra o problema da indução.
Raciocinar indutivamente é partir de premissas particulares, na busca de
uma lei geral, universal, por exemplo:
O ferro conduz eletricidade
O ferro é metal
O ouro conduz eletricidade
O ouro é metal
O cobre conduz eletricidade
O cobre é metal
UP CURSOS 2022

6. 4
Logo os metais conduzem eletricidade.
Os indutivistas acreditam que as explicações para os fenômenos advém
unicamente da observação dos fatos.
Abdução
Significa determinar a premissa. Usa-se a conclusão e a regra para defender
que a premissa poderia explicar a conclusão. Exemplo: "Quando chove, a relva
fica molhada. A relva está molhada, então deve ter chovido." Associa-se este
tipo de raciocínio aos médicos e detetives etc.
A abdução é uma das três formas canónicas de inferência para estabelecer
hipóteses científicas. As outras duas são a indução e a dedução. A abdução foi
a noção que Charles Sanders Peirce adaptou, usando-a no suposto sentido
aristotélico, e contemporaneamente é utilizada em pesquisas acadêmicas,
principalmente na Semiótica e nas Ciências da Comunicação.
A forma lógica é a seguinte: Tem-se observado B (um conjunto de dados ou
factos) e A podendo explicar B. É provável que A esteja certo. Assim, a
abdução é a inferência a favor da melhor explicação. A hipótese A, ao ser
verdadeira, explica B. nenhuma outra hipótese pode explicar tão
bem B como A. Logo, A é provavelmente verdadeira.
Na abdução utilizam-se certos dados para se chegar a uma conclusão mais
ampla, como acontece nas inferências da melhor explicação.
Na abdução, o que está implicado não é uma função de verdade, mas antes
uma relação de causalidade. A abdução estabelece a probabilidade da
conclusão da inferência e não necessariamente a sua verdade. O facto de um
conjunto de dados B poder ser o efeito da causa A, pode não permitir inferir
categoricamente uma ilação de A sobre B, dado ser uma causa possível entre
muitas outras. O mesmo efeito pode ser consequência de diferentes causas.
UP CURSOS 2022

7. 5
LÓGICAS ARGUMENTATIVAS: PROPOSIÇÕES, NEGAÇÃO,
CONJUNÇÃO, DISJUNÇÃO, CONDICIONAL, BICONDICIONAL
O termo falácia deriva do verbo latino fallere, que significa enganar. Designa-se
por falácia um raciocínio errado com aparência de verdadeiro. Na lógica e
na retórica, uma falácia é um argumento logicamente incoerente, sem
fundamento, inválido ou falho na tentativa de provar eficazmente o que alega.
Argumentos que se destinam à persuasão podem parecer convincentes para
grande parte do público apesar de conterem falácias, mas não deixam de ser
falsos por causa disso.
Por exemplo, se alguém diz:
"O fogo é quente e sei disso por dois motivos:
ele é vermelho; e
medi sua temperatura com um termômetro".
Nesse exemplo, foi de fato comprovado que o fogo é quente por meio da
premissa 2. A premissa 1 deve ser descartada como falaciosa, mas a
argumentação não está de todo destruída. O básico de um argumento é que a
conclusão deve decorrer das premissas. Se uma conclusão não é
consequência das premissas, o argumento é inválido. Deve-se observar que
um raciocínio pode incorrer em mais de um tipo de falácia, assim como que
muitas delas são semelhantes.
Proposições
São sentenças (frases) ou expressões matemáticas que possuem
indentificações lógicas.
p: Monique é modesta.
q: Gusttavo é belga
Valores Lógicos:
V (Verdadeiro)
F (Falso)
UP CURSOS 2022

8. 6
Negação ( ; ~ )
Não
Não p: Monique não é modesta.
q: Gusttavo não é belga
(~p)/(~q)
Conjunção (^)
^ e
p^q: Monique é modesta e Gusttavo é belga.
Disjunção (v)
v
ou
pv~q: Monique é modesta ou Gusttavo não é belga.
Condicional ( )
: Se ... então
~p q: Se Monique não é modesta então Gusttavo é belga.
UP CURSOS 2022

9. 7
Bicondicional ( )
: Se e somente se
p q: Monique é modesta se e somente se Gusttavo é belga.
Equívoco: Usar uma afirmação com significado diferente do que seria
apropriado ao contexto.
Exemplo: Os assassinos de crianças são desumanos. Portanto, os humanos
não matam crianças.
Joga-se com os significados das palavras. A palavra "humanos" possui vários
sentidos, pode ser um tipo de primata (sentido biológico) ou uma boa pessoa
(sentido moral), mas a falácia usa a palavra sem considerar a diferença de
sentido.
Anfibologia: Ocorre quando as premissas usadas no argumento são
ambíguas devido a sua má elaboração sintática.
Exemplo:
Venceu o Brasil a Argentina.
Ele levou o pai ao médico em seu carro.
1. Quem venceu? 2. No carro de quem?
Nesse caso, toda a frase possui sentidos diversos a depender do contexto.
Ênfase: Enfatizar uma palavra para sugerir o contrário.
Exemplo: Hoje o capitão estava sóbrio (sugerindo embriaguez).
Pronuncia-se a palavra "hoje" com muita força para sugerir que ele é um
alcoólatra.
É uma ironia.
UP CURSOS 2022

10. 8
OPERAÇÕES LÓGICAS
Operações Lógicas são utilizadas a todo o momento nos nossos códigos de
algoritmos.
Utilizamos sempre que precisamos tomar decisões. Em um algoritmo ou
programa, toda a decisão terá sempre como resposta o resultado Verdadeiro
ou Falso.
Em lógica binária, ocorrem apenas dois estados:
Verdadeiro, representado pela letra V, ou pelo número 1.
Falso, representado pela letra F, ou pelo número 0.
A disjunção é uma operação que verifica a seguinte tabela de verdade:
a b a ∨ b
V V V
V F V
F V V
F F F
ou de forma equivalente:
UP CURSOS 2022

11. 9
Iguais Verdadeiro; Diferentes Falso.
Portanto pode ainda ser representada pela soma, que dá o mesmo resultado,
se a e b forem 0 ou 1, excepto que se assume também "1+1=1" (ou seja, esta
soma disjuntiva tem um significado algébrico de a∨b ≡ a + b - ab).
Outra interpretação é a da lógica fuzzy, que generaliza pela equivalência com
o máximo(a,b).
A conjunção relaciona dois valores, mas usando o seu resultado podem ser
feitas operações com mais valores.
Com uma tabela de verdade pode demonstrar-se a propriedade associativa
é igual a
e portanto neste caso basta escrever sem necessidade de
parentesis, já que o resultado é o mesmo.
A conjunção lógica tem diversas propriedades. Destacam-se:
(comutatividade)
(associatividade)
(leis de De Morgan)
(universalidade)
(a falsidade é o elemento neutro da disjunção)
(a verdade é o elemento absorvente da disjunção)
UP CURSOS 2022

12. 10
ARRANJOS SIMPLES
Tipo de agrupamento
n elemento, q a q
Formação de números
An, p = n!
(n-p)!
Definimos permutações simples como sendo o número de maneiras de
arrumar n elementos em n posições em que cada maneira se diferencia pela
ordem em que os elementos aparecem. Aplicando o princípio da multiplicação
obtemos a seguinte equação para permutações simples:
Exemplo: Com a palavra AMOR, qual é a posição, em ordem crescente,
ocupada pela palavra ROMA.
A P3=3!=6
M _ P3=3!=6
O P3=3!=6
R A P2=2!=2
R M _ P2=2!=2
R O A P1=1!=1
R O M A P1=1!=1
24
UP CURSOS 2022

13. 11
COMBINAÇÕES SIMPLES
Na combinação, a ordem em que os elementos são tomados não é importante.
Quando a ordem não importa, mas cada elemento pode ser contado apenas
uma vez, o número de combinações é o coeficiente binomial:
Onde n é o total de elementos e r o número de elementos escolhidos.
Quando a ordem não importa, mas cada objeto pode ser escolhido mais de
uma vez, o número de combinações é:
Onde n é o total de elementos e r o número de elementos escolhidos.
C
10,4
= 10 . 9 . 8 . 7 = 210
4 . 3 . 2 . 1
C = 1
3,3
UP CURSOS 2022

14. 12
O número é igual a 52! (ou seja, "cinquenta e dois fatorial"), que é o produto de
todos os números naturais de 1 até 52. Pode parecer surpreendente o quão
enorme é esse número, cerca de 8,065817517094 × 1067. Comparando este
número com alguns outros números grandes, ele é maior que
o quadrado do Número de Avogadro, 6,022 × 1023, quantidade equivalente a
um mol".
Análise combinatória é a área da matemática que estuda os problemas
envolvendo a contagem na ocorrência de um determinado evento, sem a
necessidade de reproduzirmos todas as possibilidades.
É importante falarmos sobre fatorial pois na análise combinatória é comum o
uso de fatorial nas fórmulas.
Seja n um número natural, maior que 1, definimos fatorial de n como o produto
de todos os números naturais de n até 1.
Simbolicamente, o fatorial de n é: n!
Então, n! = n(n – 1).(n – 2) . … . 3 . 2 . 1
Exemplo:
3! = 3 . 2 . 1 = 6
10! = 10 . 9 . 8 . 7 . 6 . 5 . 4 . 3 . 2 . 1 = 3.628.800
O princípio fundamental da contagem nos permite definir uma regra de forma
que possamos determinar o número de possibilidades de ocorrência de um
evento, para que não precisamos reproduzir todas as possibilidades de
ocorrência do evento.
Então, vamos chamar de p o número de pares sapatos e c o número de cores
disponível. Onde:
p = 3;
c = 2.
Assim, fazendo o produto temos o total de possibilidades que Maria possui
para comprar 1 par de sapatos.
p . c = 3 . 2 = 6 possibilidades
UP CURSOS 2022

15. 13
TABELA VERDADE
Tabela-verdade, tabela de verdade ou tabela veritativa é um tipo de tabela
matemática usada em lógica para determinar se uma fórmula é válida ou se um
sequente é correto.
Uma tabela-verdade consiste em:
uma linha em que estão contidos todas as subfórmulas de uma fórmula. Por
exemplo, a fórmula ¬((A∧B)→C) tem o seguinte conjunto de subfórmulas:
{ ¬((A∧B)→C) , (A∧B)→C , A∧B , A , B , C}
L linhas em que estão todos possíveis valores que os termos podem receber e
os valores cujas fórmulas moleculares tem dados os valores destes termos;
o número destas linhas é L = nt , sendo n o número de valores que o sistema
permite (sempre 2 no caso do cálculo proposicional clássico) e t o número de
termos que a fórmula contém; assim, se uma fórmula contém 2 termos, o
número de linhas que expressam a permutações entre estes será 4: um caso
de ambos termos serem verdadeiros (V V), dois casos de apenas um dos
termos ser verdadeiro (V F , F V) e um caso no qual ambos termos são falsos
(F F). Se a fórmula contiver 3 termos, o número de linhas que expressam a
permutações entre estes será 8: um caso de todos termos serem verdadeiros
(V V V), três casos de apenas dois termos serem verdadeiros (V V F , V F V , F
V V), três casos de apenas um dos termos ser verdadeiro (V F F , F V F , F F
V) e um caso no qual todos termos são falsos (F F F).
Negação
A negação da proposição "A" é a proposição "~A", de maneira que se "A" é
verdade então "~A" é falsa, e vice-versa.
Obs.: Usando o Excel, tal proposição pode ser expressado da seguinte
maneira: =NÃO(C1;C2)
UP CURSOS 2022

16. 14
Conjunção
A conjunção é verdadeira se e somente se ambos os operandos são
verdadeiros.
Obs.: Usando o Excel, tal proposição pode ser expressado da seguinte
maneira: =E(C1;C2)
Disjunção
A disjunção é falsa se, e somente se ambos os operandos forem falsos.
Obs.: Usando o Excel, tal proposição pode ser expressado da seguinte
maneira: =OU(C1;C2)
Disfunção
A disfunção é necessariamente falsa, independente dos operando.
Condicional (se... então)
A condicional é falsa se, e somente se, o primeiro operando é verdadeiro e o
segundo operando é falso.
Bicondicional (se e somente se)
A bicondicional é verdadeira se, e somente se, ambos operandos forem falsos
ou ambos verdadeiros. Trata-se de um detetor de igualdade.
Disjunção exclusiva (OU EXCLUSIVO... ou XOR)
A disjunção exclusiva é verdadeira se, e somente se, apenas um dos
operandos for verdadeiro. Trata-se de um detetor de desigualdades.
Adaga de Quine (NOR)
A Adaga de Quine (negação da disjunção) é verdadeira se e somente se os
operandos são falsos.
UP CURSOS 2022

17. 15
(A∧B) ≡ ¬(B→¬A) ≡ ¬(¬A∨¬B) ≡ (¬A↓¬B)
A B ¬A ¬B A∧B B→¬A ¬(B→¬A) (¬A↓¬B)
V V F F V F V f
V F F V F V F F
F V V F F V F F
F F V V F V F F
(A→B) ≡ ¬(A∧¬B) ≡ (¬A∨B) ≡ ¬(¬A↓B)
A B ¬A ¬B A→B A∧¬B ¬(A∧¬B) ¬A∨B
V V F F V F V V
V F F V F V F F
F V V F V F V V
F F V V V F V V
(A∨B) ≡ ¬(¬A∧¬B) ≡ (¬A→B) ≡ ¬(A↓B)
A B ¬A ¬B ¬A∧¬B ¬(¬A∧¬B) ¬A→B ¬(A↓B)
V V F F F V V V
V F F V F V V V
F V V F F V V V
F F V V V F F F
UP CURSOS 2022

18. 16
PROPRIEDADES
Em matemática , uma propriedade é qualquer característica que se aplica a um
determinado conjunto.
Rigorosamente, uma propriedade p definida para todos os elementos de um
conjunto X é geralmente definida como uma função p : X → {true, false}, que é
verdadeira sempre que a propriedade é válida; ou equivalentemente, como o
subconjunto de X para o qual p é válido; ou seja, o conjunto { x | p ( x ) =
verdadeiro}; p é sua função indicadora . No entanto, pode-se objetar que a
definição rigorosa define apenas a extensão de uma propriedade e não diz
nada sobre o que faz com que a propriedade mantenha exatamente esses
valores.
Exemplos de propriedades incluem a propriedade comutativa de
números reais e complexos e a propriedade distributiva .
Em matemática, uma operação binária é comutativa se alterar a ordem dos
operandos não alterar o resultado. É uma propriedade fundamental de muitas
operações binárias, e muitas provas matemáticas dependem disso. Mais
conhecido como o nome da propriedade que diz "3 + 4 = 4 + 3" ou "2 × 5 =
5 × 2" , a propriedade também pode ser usada em configurações mais
avançadas. O nome é necessário porque existem operações, como divisão e
subtração, que não o possuem (por exemplo, "3 - 5 ≠ 5 - 3" ); tais
operações não sãocomutativas e, portanto, são chamadas de operações não
comutativas . A idéia de que operações simples, como a multiplicação e
adição de números, são comutativas foi assumida por muitos anos
implicitamente. Assim, essa propriedade não foi nomeada até o século XIX,
quando a matemática começou a se formalizar.
Existe uma propriedade correspondente para relações binárias ; uma relação
binária é considerada simétrica se a relação se aplicar independentemente da
UP CURSOS 2022

19. 17
ordem de seus operandos; por exemplo, igualdade é simétrica, pois dois
objetos matemáticos iguais são iguais, independentemente de sua ordem.
Em matemática , a propriedade distributiva das operações binárias generaliza a
lei distributiva da álgebra booleana e álgebra elementar. Na lógica
proposicional, a distribuição se refere a duas regras válidas de substituição
. As regras permitem reformular conjunções e disjunções dentro de provas
lógicas .
Por exemplo, em aritmética:
2 ⋅ (1 + 3) = (2 ⋅ 1) + (2 ⋅ 3), mas 2 / (1 + 3) ≠ (2/1) + (2/3)
No lado esquerdo da primeira equação, o 2 multiplica a soma de 1 e 3; no lado
direito, multiplica o 1 e o 3 individualmente, com os produtos adicionados
posteriormente. Como estas fornecem a mesma resposta final (8), diz-se que a
multiplicação por 2 distribui a adição de 1 e 3. Dado que alguém poderia
colocar quaisquer números reais no lugar de 2, 1 e 3 acima, e ainda assim
obter uma equação verdadeira, a multiplicação de números reais é distribuída
pela adição de números reais.
A multiplicação de números ordinais, por outro lado, é apenas distributiva à
esquerda, e não à direita.
O produto cruzado é distribuído à esquerda e à direita sobre a adição de
vetores , embora não seja comutativo.
A união de conjuntos é distributiva por interseção , e a interseção é distributiva
por união.
A disjunção lógica ("ou") é distributiva sobre a conjunção lógica ("e") e vice-
versa.
Para números reais (e para qualquer conjunto totalmente ordenado ), a
operação máxima é distributiva sobre a operação mínima e vice-versa: max
( a , min ( b , c )) = min (max ( a , b ), max ( a , c )) e min ( a , max ( b , c )) =
max (min ( a , b ), min ( a , c )) .
Para números inteiros , o maior divisor comum é distributivo sobre o múltiplo
menos comum e vice-versa: gcd ( a , lcm ( b , c )) = lcm (gcd ( a , b ), gcd
( a , c )) e lcm ( a , gcd ( b , c )) = gcd (lcm ( a , b ), lcm ( a , c )) .
UP CURSOS 2022

20. 18
Para números reais, a adição é distribuída na operação máxima e também na
operação mínima: a + max ( b , c ) = max ( a + b , a + c ) e a + min ( b , c ) =
min ( a + b , a + c ) .
Para multiplicação binomial , a distribuição às vezes é chamada de FOIL
Method [2] (Primeiros termos ac , Outer ad , Inner bc e Last bd ), como: ( a + b )
· ( c + d ) = ac + ad + bc + bd .
A multiplicação polinomial é distributiva sobre a adição polinomial.
A multiplicação de números complexos é distributiva:
Comutatividade é uma propriedade de operações binárias, ou de ordem mais
alta, em que a ordem dos operandos não altera o resultado final.
Por mais que a noção comum de aritmética possam sugerir que esta
propriedade seja óbvia, ela é importante para organizar os tipos de operações
de grupos de acordo a propriedade de comutatividade ou não. E mesmo na
aritmética existem exemplos de operações que não são comutativas, como
a subtração e divisão.
Dado um conjunto qualquer S e um operação binária f, dizemos que f é
comutativa se:
A notação matemática mais comum para operações binárias é através de um
símbolo gráfico entre os dois operandos, por exemplo, escreve-se:
Usando esta notação, a definição de comutatividade fica:
UP CURSOS 2022

21. 19
ANÁLISE COMBINATÓRIA
Segundo Wieleitner o problema mais antigo que se relaciona com a teoria dos
números e com a Análise Combinatória, é o da formação dos quadrados
mágicos. Chamamos de quadrados mágicos (de ordem n) um arranjo de
números 1,2,3...n2 em um quadrado n n de forma que cada linha, coluna e
diagonal deste quadrado possua a mesma soma. Como vemos abaixo:
O primeiro quadrado mágico conhecido é o Lo Shu, que segundo Needham
(1959) data do século I d.C., mas que pode ser tão antigo a ponto de ter sido
escrito por volta de 2000 a.C. (Berge, 1971):
UP CURSOS 2022

22. 20
Este diagrama está associado às nove salas do palácio mítico de Ming Thang,
onde vários ritos eram realizados, sendo que a substituição destes símbolos
por números inteiros determina o famoso quadrado mágico denominado
Saturn. Este quadrado causava uma grande fascinação para a maioria das
pessoas, pois nesta época, mesmo a mais simples aritmética era algo
espantoso. Acredita-se que a idéia dos quadrados mágicos foi transmitida
pelos chineses para os árabes, que fizeram grandes contribuições e
construíram quadrados maiores que o antigo Lo Shu.
É um ramo da Matemática que permite que se escolha, arrume e conte o
número de elementos de determinado conjunto, sem que haja necessidade de
enumerá-los. Cada um desses problemas é um desafio para os alunos, pois
exige flexibilidade de pensamento: é necessário parar, concentrar, discutir e
pensar para poder resolvê-los. As operações combinatórias são essenciais
para o desenvolvimento cognitivo, por isso seria de extrema importância que o
aluno tivesse contato com esse tópico desde os primeiros anos da escola
básica, para familiarizar-se com problemas de contagem, descrevendo os
casos possíveis e contando-os através de uma representação por ele
escolhida, sem regras em princípio, de modo que ele adquirisse um método
sistemático e gradativo para a resolução dos problemas, visando uma posterior
formalização no ensino médio.
Espaço amostral: Conjunto de todos os possíveis resultados.
(Experimento aleatório)
Evento: Qualquer subconjunto do espaço amostral.
Exemplo: De um trabalho de 52 Cartas tira-se ao acaso uma das cartas.
Determine a probabilidade:
a) Uma dama;
b) Uma dama de paus;
c) Uma carta de ouros.
52 Cartas = 13 Copas; 13 Ouros; 13 Espadas; 13 Paus.
Resposta: a) P= 4/52 = 1/3; b) P= 1/52; c) P= 13/52 = ¼
UP CURSOS 2022

23. 21
A REGRA DE TRÊS
A regra de três, na matemática, é uma forma de se descobrir uma quantidade
que tenha para outra conhecida a mesma relação que têm entre si entre outros
dois valores numéricos conhecidos. Existem dois tipos de regra de três:
simples e composta.
Serve para se descobrir um único valor a partir de outros três. Relacionam-se
quatro valores, divididos em dois pares de mesma grandeza e unidade
interdependentes e relacionadas.
Matematicamente, são o primeiro par de mesma grandeza e unidade,
e são o segundo par, também de mesma grandeza e unidade.
Se as grandezas associadas forem GDP (grandezas diretamente
proporcionais), deve-se usar a relação de proporção direta:
Se as grandezas forem GIP (grandezas inversamente proporcionais), deve-se
usar a relação de proporção inversa:
Regra de 3 Composta: É usada quando para se descobrir um valor, não basta
utilizar no cálculo apenas três dos valores dados.
UP CURSOS 2022

24. 22
a1.b2 = a2.b1
A regra de três simples é usada para encontrar um quarto valor que não
conhecemos, desde que conheçamos apenas três dos valores no problema.
Diretamente proporcional
Se as grandezas forem diretamente proporcionais montamos
uma proporção em que um dos valores abaixo é desconhecido, assim:
Inversamente proporcional
Se as grandezas forem inversas, então montamos uma das proporções, sendo
um dos valores a incógnita, assim:
Como é inversamente proporcional invertemos uma das razões, depois
calculamos para achar o valor desconhecido.
UP CURSOS 2022

25. 23
Essas setas guias servem para você lembrar que tem que fazer a inversão de
uma das razões na proporção para não errar no cálculo e encontrar uma
resposta diferente. Feito a inversão temos a seguinte proporção:
Resolva o problema para encontrar o valor de x.
Logo, para encher o tanque com apenas 4 torneiras precisaremos de 33
minutos.
Veja que multiplicamos a proporção em forma de cruz para encontrar o valor
de x. Esse valor desconhecido resolve o problema proposto.
UP CURSOS 2022

26. 24
Referências Bibliográficas
Wikipédia, a enciclopédia livre. Raciocínio lógico.
Disponível em:
https://pt.wikipedia.org/wiki/Racioc%C3%ADnio_l%C3%B3gico
Wikipédia, a enciclopédia livre.Método dedutivo.
Disponível em:
https://pt.wikipedia.org/wiki/M%C3%A9todo_dedutivo
Wikipédia, a enciclopédia livre.Método indutivo.
Disponível em:
https://pt.wikipedia.org/wiki/M%C3%A9todo_indutivo
Wikipédia, a enciclopédia livre.Abdução (lógica filosófica).
Disponível em:
https://pt.wikipedia.org/wiki/Abdu%C3%A7%C3%A3o_(l%C3%B3gica_filos%C3
%B3fica)
Wikipédia, a enciclopédia livre.Falácia.
Disponível em:
https://pt.wikipedia.org/wiki/Fal%C3%A1cia
Ingrid Carvalho.Operações Lógicas.
Disponível em:
UP CURSOS 2022

27. 25
https://medium.com/@ingrid.carvalho.mo/opera%C3%A7%C3%B5es-
l%C3%B3gicas-c9e4c4e7ab0c
Wikipédia, a enciclopédia livre.Disjunção lógica.
disponível em:
https://pt.wikipedia.org/wiki/Disjun%C3%A7%C3%A3o_l%C3%B3gica
Wikipédia, a enciclopédia livre.Combinatória.
Disponível em:
https://pt.wikipedia.org/wiki/Combinat%C3%B3ria
Matemática Básica. Análise Combinatória: Fórmulas e Resumo.
Disponível em:
https://matematicabasica.net/analise-combinatoria/
Wikipédia, a enciclopédia livre.Tabela-verdade.
Disponível em:
https://pt.wikipedia.org/wiki/Tabela-verdade
Wikipédia, a enciclopédia livre.Propriedade comutativa.
Disponível em:
https://en.wikipedia.org/wiki/Commutative_property
Wikipédia, a enciclopédia livre. Propriedade (matemática).
Disponível em:
https://en.wikipedia.org/wiki/Property_(mathematics)
UP CURSOS 2022

28. 26
Wikipédia, a enciclopédia livre.Propriedade distributiva.
Disponível em:
https://en.wikipedia.org/wiki/Distributive_property
Wikipédia, a enciclopédia livre.Comutatividade.
Disponível em:
https://pt.wikipedia.org/wiki/Comutatividade
Cristiane Maria Roque Vazquez.UNESP - Rio Claro.Fabiane Cristina Höpner
Noguti.UNESP - Rio Claro.
Disponível em:
http://www.sbem.com.br/
Wikipédia, a enciclopédia livre.Regra de três.
Disponível em:
https://pt.wikipedia.org/wiki/Regra_de_tr%C3%AAs
Matemática Básica. Regra de Três Simples: Direta e Inversa.
Disponível em:
https://matematicabasica.net/regra-de-tres-simples/
UP CURSOS 2022