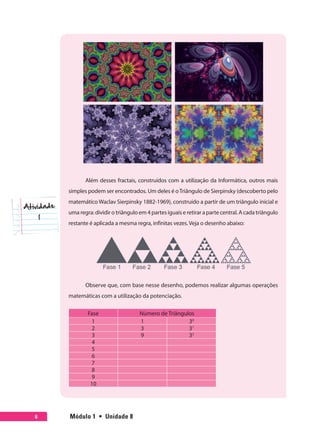
O documento discute potenciação e radiciação, operações matemáticas úteis para representar números grandes de forma mais simples e para resolver problemas sobre a disseminação de informações em redes sociais. Exemplos mostram como potenciações podem ser usadas para calcular quantas pessoas ficariam sabendo de um boato em determinados períodos de tempo dependendo do tamanho da rede de cada pessoa.