A seção apresenta o conceito, evolução e objetivos da econometria. A econometria surgiu para estabelecer relações quantitativas entre variáveis econômicas, fundamentando teorias econômicas com dados. Seu objetivo é medir fenômenos econômicos e testar hipóteses, utilizando matemática, estatística e teoria econômica.

1. Econometria

3. Regina Lúcia Sanches Malassise
Econometria

4. Dados Internacionais de Catalogação na Publicação (CIP)
Malassise, Regina Lucia Sanches
M238e Econometria / Regina Lucia Sanches Malassise. –
Londrina: Editora e Distribuidora Educacional S. A., 2015.
192 p.
ISBN 978-85-8482-206-5
1. Econometria. 2. Regressão. I. Título
CDD 330.015195
© 2015 por Editora e Distribuidora Educacional S. A.
Todos os direitos reservados. Nenhuma parte desta publicação poderá ser reproduzida
ou transmitida de qualquer modo ou por qualquer outro meio, eletrônico ou mecânico,
incluindo fotocópia, gravação ou qualquer outro tipo de sistema de armazenamento e
transmissão de informação, sem prévia autorização, por escrito, da Editora e Distribuidora
Educacional S. A.
Presidente: Rodrigo Galindo
Vice-Presidente Acadêmico de Graduação: Rui Fava
Diretor de Produção e Disponibilização de Material Didático: Mario Jungbeck
Gerente de Produção: Emanuel Santana
Gerente de Revisão: Cristiane Lisandra Danna
Gerente de Disponibilização: Nilton R. dos Santos Machado
Editoração e Diagramação: eGTB Editora
2015
Editora e Distribuidora Educacional S. A.
Avenida Paris, 675 – Parque Residencial João Piza
CEP: 86041-100 — Londrina — PR
email: editora.educacional@kroton.com.br
Homepage: http://www.kroton.com.br/

5. Sumário
Unidade 1 | Conceitos introdutórios e especificação de modelos
econométricos
Seção 1 - Conceito, evolução e objetivos da econometria
1.1 O conceito de econometria
1.2 Evolução da econometria
1.3 Objetivos da econometria
1.3.1 Divisão da econometria e análise de regressão
Seção 2 - Conceito e classificação de modelos
2.1 Modelo: conceito e tipos
2.1.1 Estrutura de modelos econométricos
2.1.2 Classificações mais comuns de modelos econométricos
2.1.3 Modelos econométricos e suas qualidades
2.1.4 As etapas da modelagem econométrica
Seção 3 - Especificação de modelos
3.1 Requisitos básicos de um modelo
3.2 Fontes de informações necessárias à especificação de modelos
3.3 A expressão matemática adequada ao modelo linear
3,4 Alguns critérios para auxiliar a escolha da forma funcional
3.5 Limitações da econometria
09
13
14
16
18
19
21
21
24
25
27
28
37
37
40
44
48
50
Unidade 2 | Modelo linear geral e inclusão de variáveis especiais
Seção 1 - O método dos mínimos quadrados ordinários (MQO)
1.1 A regressão linear
1.2 Método dos mínimos quadrados ordinários (MQO) e pressupostos
do modelo
1.2.1 Pressupostos básicos do MQO
1.2.2 As implicações da violação dos pressupostos
1.2.3 Os estimadores MQO são BLUE
1.3 A estimação do modelo por meio do MQO
1.3.1 Análise dos resíduos
1.3.2 Modelo linear simples: exemplo numérico
55
59
59
61
61
63
64
67
69
71

6. Unidade 4 | Ferramentas e aplicações da econometria
Seção 1 - Consumo de energia elétrica e PIB no Brasil 1970-1996
1.1 Breve discussão teórica sobre o tema
1.2 Hipótese
1.3 Modelo econométrico
1.4 Estimativa do modelo
1.5 Conclusão
Seção 2 - Avaliação de Modelos Estimados
2.1 Qualidades desejáveis dos estimadores MQO
2.1.1 Não tendenciosidade
2.1.2 Eficiência ou variância mínima
2.1.3 Consistência
2.2 Critérios para avaliar as estimativas de um modelo
2.2.1 Deduções matemáticas da média, variância e covariância
2.3. Quadro de análise de variância
Seção 3 - Modelo de Regressão Múltiplo
3.1 O processo abreviado de estimativa do modelo geral
75
75
77
77
78
78
80
82
87
87
101
105
106
109
109
111
113
114
114
116
119
119
120
121
123
123
124
127
127
128
129
147
151
151
152
152
153
156
Unidade 3 | Violação dos pressupostos básicos do modelo
Seção 1 - Implicações das violações dos pressupostos básicos
do MQO
1.1 Principais formas de violação dos pressupostos
Seção 2 - Multicolinearidade
2.1 Conceito
2.1.1 Principais fontes de multicolinearidade
2.1.2 Casos de multicolinearidade
2.2 Diagnóstico de multicolinearidade
2.2.1 Testes que permitem identificar a presença de
multicolinearidade
2.2.2 Consequências da multicolinearidade
2.3 Consequências da multicolinearidade
Seção 3 - Autocorrelação ou correlação serial
3.1 Conceito
3.2 Diagnóstico de autocorrelação: o teste d de Durbin
3.2.1 Implementação do teste de Durbin
3.3 Medidas corretivas de autocorrelação
3.3.1 Quando a estrutura da autocorrelação é conhecida
3.3.2 Quando a estrutura da autocorrelação é desconhecida
Seção 4 - Heterocedasticidade
4.1 Conceito
4.2 Identificação da heterocedasticidade
4.2.1 Testes estatisticos para identificacao da heterocedasticidade

7. Seção 2 - Estudo do desempenho da educação
2.1 Metodologia
2.2 Descrição das variáveis selecionadas sobre a escola
2.3 Formulação da hipótese de trabalho e análise das estimativas
2.4 Possibilidades e alternativas de solução para os problemas do modelo
2.5 Considerações finais
Seção 3 - Estudo sobre a criminalidade
3.1 Breve explanação sobre a economia do crime
3.2 Algumas considerações sobre os modelos com dados em painel
3.3 Painel de dados com modelos estáticos
3.3.1 Modelo de regressão pooled
3.3.2 Modelo de efeitos fixos
3.3.3 Modelo com efeitos aleatórios
4.1 Modelos de painel de dados estáticos: resultados
4.1.1 Regressão Pooled
4.1.2 Modelo de efeito fixo
4.1.3 Efeito aleatório ou randômico
4.1.4 Entre o efeito fixo e aleatório
5.1 Considerações finais
157
159
159
162
170
175
177
177
179
180
180
181
182
182
182
183
184
185
187

9. Apresentação
Um dos grandes pressupostos da formação do economista é que ele compreenda
e saiba utilizar métodos econométricos. Boa parte desta crença vem do fato de
que a economia precisa fundamentar empiricamente seus conhecimentos, isto é,
produzir provas de que as teorias realmente se aplicam à realidade estudada.
Neste sentido, os estudos ligados à Econometria têm por objetivo levar o aluno a
compreender o desenvolvimento e a implementação dos métodos econométricos.
Em cursos introdutórios como o nosso, o objetivo é compreender a ferramenta
econométrica análise de regressão. Através desta é possível utilizar o Método dos
Mínimos Quadrados Ordinários (MQO), que estão presentes na maior parte das
publicações e pesquisas econômicas.
Desta forma, neste livro contempla-se a apresentação dos caminhos seguidos
para o desenvolvimento do método econométrico. Para tanto se apresentam os
conceitos básicos, a análise de regressão, o modelo linear simples e múltiplo, bem
como se explica a operacionalização de alguns deles. Para contemplar estes temas
o livro está organizado em quatro unidades.
Na Unidade 1 aborda-se o conceito de econometria, bem como a importância de
sua utilização como método de pesquisa e de tomada de decisão. Desta forma,
você compreenderá a abrangência e limitações da econometria na apresentação de
propostas e mensuração de resultados.
Na Unidade 2 aborda-se o modelo de regressão linear simples e múltiplo, bem como
a inclusão de variáveis especiais para promover uma melhor adequação do modelo
a situações especiais. Neste sentido, você compreenderá as etapas e a implantação
destes modelos de regressão.
Na Unidade 3 estudamos os principais problemas que surgem da violação dos
pressupostos do Método dos Mínimos Quadrados (MQO), buscando compreender
como as medidas e soluções propostas para superar tais problemas podem contribuir
para melhorar os estimadores de um modelo.
Na Unidade 4, você terá a oportunidade de conhecer mais algumas ferramentas da
Econometria, bem como aplicações, pois a unidade está apresentada em forma de
composição de artigos. Assim, a explicação da forma como foi construído cada um
dos artigos permite a você compreender melhor os aspectos básicos da modelagem
econométrica.

10. Ao final do estudo deste livro você terá absorvido conhecimentos básicos de
Econometria que lhe permitam ler e também trabalhar com técnicas econométricas
do MQO. Desejo a você bons estudos!

11. Unidade 1
CONCEITOS
INTRODUTÓRIOS E
ESPECIFICAÇÃO DE
MODELOS ECONOMÉTRICOS
Nesta seção são apresentados o conceito, a evolução e os objetivos da
econometria.
Nesta seção abordam-se os conceitos básicos de um modelo
econométrico.
Nesta seção estudaremos as exigências e necessidades da especificação
de modelos econométricos.
Seção 1 | Conceito, evolução e objetivos da econometria
Seção 2 | Conceito e classificação de modelos
Seção 3 | Especificação de modelos
Objetivos de aprendizagem: Nesta unidade, você será levado a compreender o
que é econometria, bem como a importância de sua utilização como método de
pesquisa e de tomada de decisão. Ao final da leitura, compreenderá a abrangência
e limitações da econometria na apresentação de propostas e mensuração de
resultados.
Para que você compreenda o que é econometria, suas implicações e abrangência,
esta unidade está subdividida em três seções.
Regina Lúcia Sanches Malassise

12. Conceitos introdutórios e especificação de modelos econométrico
U1
10

13. Conceitos introdutórios e especificação de modelos econométrico
U1
11
Introdução à unidade
A econometria é uma área e, ao mesmo tempo, um método de estudo utilizado
em diversas áreas do conhecimento, porém de maneira mais profunda nos estudos
econômicos.
Nos cursos de Economia, ela constitui-se numa disciplina fundamental para fixar
as bases quantitativas dos conhecimentos da teoria econômica. Assim, pode ser
conhecida também como ‘medição econômica’, que é a tradução literal da palavra
econometria.
A disciplina em si necessita de um conjunto de conhecimentos que englobam
matemática, estatística e teoria econômica. Porém, difere de todas elas devido
à aplicabilidade que faz dos conhecimentos destas áreas. Difere da matemática
porque busca fundamentar os resultados obtidos utilizando-se das teorias
econômicas, difere da estatística porque busca estabelecer relações de causa e
efeito entre as grandezas mensuradas, difere da teoria econômica porque busca
estabelecer relações quantitativas concretas para as leis econômicas para as quais
a teoria se ocupa mais de modo geral e esquemático. Dando continuidade, vamos
para o estudo desta unidade.

14. Conceitos introdutórios e especificação de modelos econométrico
U1
12

15. Conceitos introdutórios e especificação de modelos econométrico
U1
13
Seção 1
Conceito, evolução e objetivos da econometria
Introdução à seção
Em quase todas as áreas de Ciências Sociais Aplicadas surge, em determinado
momento, a necessidade de trabalhar relações quantitativas para que as ferramentas
de análise de dados permitam refutar ou aceitar uma conclusão que existia a priori
e que se deseja confirmar através dos dados.
Tal situação não é diferente com a economia, em especial a Teoria Econômica
enquanto pensamento constituído e sistematizado sobre o funcionamento geral
da atividade econômica, também buscou relações quantitativas para fundamentar
os conhecimentos que existiam a priori.
A Teoria Econômica refere-se à sistematização conceitual dos processos
e fenômenos econômicos ou reconstrução abstrata da realidade
econômica, fazendo uso das categorias de um método de investigação.
A teoria econômica procura encontrar as determinações essenciais dos
fenômenos econômicos, separando o acessório do fundamental, com
isso estabelecendo formulações universais, num trabalho de síntese.
É por meio da teoria que a economia se entrelaça com a história, a
sociologia, a antropologia e outras ciências afins. Seu papel não se limita
à interpretação do que ocorre no plano da produção, da circulação e do
consumo: é também o ponto de partida para a formulação de respostas
aos problemas econômicos surgidos em cada etapa do desenvolvimento
social.
Assim, a econometria surge como uma área de conhecimento específico
da economia e que visa, através do estudo de dados, estabelecer relações
quantitativas (através da matemática e estatística) e econômicas (através
da Teoria Econômica) na investigação sobre temas econômicos de
pesquisa. Neste sentido, partimos da compreensão do conceito de
econometria para explorar a dimensão e abrangência desta área de
conhecimento da economia.

16. Conceitos introdutórios e especificação de modelos econométrico
U1
14
1.1 O conceito de econometria
É interessante notar que a curiosidade humana nos leva a desenvolver soluções,
e neste caminho criam-se métodos. Isto é, desenvolvem-se formas de proceder
que permitam imitar um evento observado e a partir dele criar alguma forma de
mensuração que permita, de certa forma, prever algum resultado que seja o mais
próximo possível da realidade.
Assim, o termo “econometria” foi apresentado em 1926 pelo economista Ragnar
Frisch, de origem norueguesa, que se baseou na palavra “biometria”, que já era
utilizada desde o século XIX, para referir-se aos estudos biológicos que empregavam
métodos estatísticos.
Em particular, a biometria procurava identificar uma característica específica a
partir da observação de organismos de uma mesma espécie. Assim, por exemplo,
ao identificar a altura dos homens em um grupo grande de pessoas, verificou-
se que certa altura aparecia com mais frequência, e o número de homens com
alturas diferentes desta (maiores ou menores) estavam simetricamente distribuídos
de cada lado (maior ou menor). A esta observação a estatística atribuiu o nome
de Lei da Distribuição Normal. A representação gráfica de tal situação pode ser
visualizada na Figura 1.1:
O significado da Lei da Distribuição Normal é que, se retirarmos uma amostra de
uma população para analisar uma determinada característica, a característica que
aparece com maior frequência numa determinada amostra é a média. No caso da
altura dos homens, tal estudo constatou que a altura mais frequente entre homens
adultos é 1,75 m, que corresponde à média das estaturas observadas. A curva
representada na Figura 1.1 é a curva de distribuição normal também conhecida
como curva de Gauss-Laplace.
Figura 1.1 – Representação da distribuição da altura de homens adultos
Fonte: O autor (2015).

17. Conceitos introdutórios e especificação de modelos econométrico
U1
15
Esta foi, então, a primeira ideia de como nasceu a econometria. Porém, ela voltou-
se para a aplicação econômica de seus métodos, logo ela pode ser definida como:
Hill (2010) argumenta que a econometria se utiliza de Teoria Econômica e de
Dados da economia, negócios e ciências sociais e estatística para responder a
questões do tipo quanto. Assim, questões tais como: quanto crescerão as vendas
de uma empresa, qual o impacto dos gastos com publicidade na eleição de um
vereador, qual o incremento de renda necessário para elevar o consumo médio
de carne de primeira etc. Então, a econometria permite prever quanto, por isto
também pode ser utilizada para previsão. Agora, vamos ver um pouco sobre a
evolução da econometria.
Em sua turma, qual a é idade média dos estudantes?
Econometria é a ciência que lida com a determinação,
por métodos estatísticos, das leis quantitativas concretas
que ocorrem na vida econômica [...] está ligada à teoria
econômica e à estatística econômica e tenta por métodos
matemáticos e estatísticos dar expressão concreta e
quantitativa às leis gerais e esquemáticas estabelecidas pela
teoria econômica (LANGE, 1961, p. 13-14).
Para entender o que é distribuição normal, é necessário, primeiramente,
definir evento aleatório. Trata-se de um evento cuja ocorrência
individual não obedece a regras ou padrões que permitam fazer
previsões acertadas, como, por exemplo, qual face de um dado lançado
cairá para cima. Muitos dos conjuntos de eventos aleatórios apresentam
padrões que não são identificáveis em cada evento isoladamente,
mas verifica-se a tendência de os eventos se concentrarem próximos
a uma posição que representa uma média matemática deles. Assim, a
quantidade de eventos diminui constante e gradativamente à medida
que nos afastamos da média.

18. Conceitos introdutórios e especificação de modelos econométrico
U1
16
1.2 Evolução da econometria
Embora o uso do termo econometria tenha sido feito por Ragnar Frisch em 1926, o
interesse por estudos e análises empíricas surge com a teoria de Cournot em 1838.
O desenvolvimento da Teoria de Duopólio, de Agustin Cournot, pela qual as
quantidades ofertadas no mercado surgem da ação e reação de dois vendedores,
obedecendo a algumas regras específicas. Estabelecem-se, então, funções
lineares e com a resolução de um sistema de equações simultâneas, através do
qual é possível estabelecer quantidade, preço e lucros de equilíbrio em duopólio.
Chamou a atenção para a busca de investigação empírica sobre oferta.
Também a obra de Alfred Marshall (1890) em que ganhou destaque a análise
do equilíbrio de mercado entre a oferta e demanda, chamaram a atenção para
estudos e investigação empírica sobre a demanda.
Por outro lado, os estudos estatísticos e econométricos só foram desenvolvidos
anos depois das pesquisas de Cournot e Marshall. Isto ocorreu devido à dificuldade
e à escassez de dados confiáveis e compilados que permitissem realizar um estudo
de verificação empírica dos conceitos teóricos.
Depois que Ragnar Frisch utilizou a palavra “econometria” pela primeira vez, em
1926, ele dedicou-se à criação da Econometric Society, em 1930, e ao jornal
Econometrica, em 1933. Em 1943, Trygve Haalvelmo publica o livro The Probability
Approach in Econometrics, obra na qual propõe que a análise estatística poderia
ser utilizada como ferramenta para validar teorias matemáticas sobre atividade
econômica com o uso de dados de fontes complexas. E os estudos que utilizam
econometria foram avançando e se desenvolvendo. Utilizando os estudos de
Matos (1995) podemos ver alguns pontos de destaque deste desenvolvimento.
• Em 1932, ocorre a fundação da Comissão Cowles, cujo objetivo era
estimular o uso da lógica, da matemática e de métodos estatísticos para
conduzir estudos de análise econômica.
• Em 1933, publica-se a primeira edição da revista Econométrica.
• Em 1934, estudos de Frisch permitem identificar os primeiros problemas
da regressão, como a multicolinearidade.

19. Conceitos introdutórios e especificação de modelos econométrico
U1
17
• Em 1939, publicam-se os estudos de Tinbergen sobre modelos
macroeconômicos multiequacionais.
• Em 1943, a publicação dos estudos de Trygve Haalvelmo destaca a
metodologia e a importância de equações interdependentes, o que deu
origem a método de estimação por equações simultâneas.
• Entre 1943 e 1954, foi elaborado o tratado de Econometria intitulado
Statistical Inference in Dynamic Economic Models, que trazia como destaque
os problemas de especificação e simultaneidade de equações.
• Depois de 1954, ocorreram grandes desenvolvimentos quando a
incorporação de novos métodos e recursos computacionais conseguiram
permitir avanços e utilizações em diversas outras áreas de estudo.
• No Brasil, somente na década de 1970, começaram a aparecer as
traduções dos manuais e livros de econometria, com as quais foi possível
difundir o estudo desta área.
• Em 1979, funda-se a Sociedade Brasileira de Econometria (SBE) e acontece
também o primeiro encontro anual de econometria.
A colinearidade é um termo que, em estatística, designa uma elevada
correlação entre duas variáveis, isto é, ambas têm a mesma trajetória
linear. Numa análise de regressão, duas variáveis independentes
podem estar altamente correlacionadas, mantendo entre si elevada
colinearidade, de tal forma que não é possível estabelecer o efeito de
cada uma delas sobre a variável dependente. Por exemplo, a elevação
das vendas de um produto (variável dependente) pode ter sido
influenciada por um aumento de salários e pela redução das taxas de
juros, não sendo possível distinguir no curto prazo qual das variáveis
independentes teve a influência maior. Nesse caso, pode-se utilizar
apenas a variável independente julgada a mais importante (o aumento
de salários, no caso), ou combinar as duas variáveis independentes
numa só, ou ainda escolher uma terceira que substitua as duas primeiras.
Quando existe um grau de correlação muito elevado, com mais de duas
variáveis, o fenômeno é denominado multicolinearidade.

20. Conceitos introdutórios e especificação de modelos econométrico
U1
18
• Em abril de 1981, publica-se a Revista de Econometria da SBE.
• A partir de 1985 a disciplina tornou-se obrigatória nos cursos de Economia.
• Hoje, a econometria é ampla e seus métodos estão difundidos nas mais
diversas áreas de estudo.
De posse do conceito e da perspectiva histórica do desenvolvimento da econo-
metria podemos discutir seus objetivos.
1.3 Objetivos da econometria
Considerando que econometria é a integração da teoria econômica, matemática
e técnicas estatísticas e que esta integração visa testar hipóteses sobre fenômenos
econômicos, estimação de coeficientes de relações econômicas e projeções
ou predições de valores futuros das variáveis ou fenômenos econômicos, Matos
(1995) aponta que são propósitos da econometria:
a) A mensuração de variáveis e agregados econômicos. Podemos citar como
exemplo a possibilidade de estimar a oferta agregada por meio da estimação do
PIB ou a demanda agregada por meio da estimação do consumo pessoal.
b) A estimação de parâmetros de relações estabelecidas pela teoria econômica
ou outro conhecimento a priori. Podemos citar como exemplo a estimação da
quantidade demanda em relação ao preço e constatarmos a aplicação ou não da
Lei Geral da Demanda para um produto específico.
c) A formulação e teste de hipóteses sobre o comportamento da realidade. Podemos
postular que o consumo de energia elétrica se mantenha constante no horário
de verão no que se refere ao consumo industrial, e a partir de aí levantar dados,
realizar regressões e testes que permitam validar ou refutar tal hipótese.
Tendo em vista estes propósitos, podemos então verificar que os objetivos da
econometria são:
a) A verificação de teorias econômicas: Diferentemente dos períodos anteriores,
hoje, é possível e necessário verificar a aplicabilidade da teoria econômica à
especificidade de estudos e pesquisas realizadas de tal forma que qualquer teoria
passe a ser utilizada e estabelecida a partir do uso de um teste empírico.
b) A avaliação de políticas econômicas: Conhecer o valor numérico de parâmetros,

21. Conceitos introdutórios e especificação de modelos econométrico
U1
19
tais como: elasticidades, multiplicadores, coeficientes técnicos, é muito importante
no processo decisório em empresas (públicas ou privadas) e no âmbito governa-
mental, dado que auxilia na comparação de efeitos resultantes de decisões alter-
nativas. Um exemplo comum é quando se faz a seguinte pergunta: se o governo
quiser aumentar a arrecadação tributando o consumo, esta política seria eficaz
em produto elástico ou inelástico. A resposta para a questão recai normalmente
sobre os preços inelásticos, pois, aumento de impostos aumenta o preço e reduz
a demanda de produtos elásticos mais que o aumento de preços, já para os pro-
dutos inelásticos a queda no consumo é menor que o aumento de preços. Por
outro lado, para determinar a elasticidade de um produto, necessitamos recorrer
à econometria.
c) A previsão de valores futuros de variáveis de natureza econômica: para os
governos na formulação de políticas, é importante que sejam conhecidas as mag-
nitudes econômicas em toda sua dimensão possível. Assim, entender os movi-
mentos de longo prazo (cíclicos) e de médio prazo (tendência) através da medição
e predição de valores futuros destas magnitudes utilizando informações passadas e
presentes. Desta forma, os governos podem fazer um julgamento da necessidade
ou não de alguma medida corretiva. Tais estudos também se aplicam às empresas.
São mais comuns os estudos de curto e médio prazo.
1.3.1 Divisão da econometria e análise de regressão
Para melhorar e direcionar os estudos a econometria está subdividida em econo-
metria teórica e aplicada. Na econometria teórica estuda-se a estruturação dos
modelos teóricos existentes, busca-se avançar propondo novas modelagens que
sejam mais adequadas ou que permitam solucionar algum problema de adequação
dos modelos existentes.
Na econometria aplicada fazem-se aplicações dos modelos existentes, cuja es-
colha é guiada por algum conhecimento a priori sobre os problemas encontra-
dos em um campo particular dos estudos da economia ou outras áreas na qual
a econometria seja relevante na busca de alternativas de solução. Em economia,
a econometria se aplica a problemas microeconômicos (microeconometria), em
estudos que envolvam a teoria da demanda, produção, investimento, consumo e
outros campos de pesquisa econômica aplicada. E também a diversas outras áreas
de estudo da economia.
Em qualquer caso, a econometria é parte arte e parte ciência, devido a muitas vezes
a intuição e o bom julgamento do econometrista desempenharem um papel
importante na escolha de um modelo econométrico apropriado.

22. Conceitos introdutórios e especificação de modelos econométrico
U1
20
Uma das formas tradicionais de estudo da Econometria Aplicada na Economia é a
análise de regressão. A análise de regressão pressupõe a existência de, no mínimo,
duas variáveis: uma variável dependente/explicada (por exemplo Y) e uma variável
independente/explicativa (por exemplo X). Um exemplo disto é a Lei da demanda,
na qual dizemos que a quantidade demanda (que podemos associar a letra Y) de-
pende inversamente do preço (que podemos associar a letra X).
Assim, enquanto na regressão, procuramos um valor para Y tomando por base
um conjunto de informações fornecido pelas características X, isto é (E[Y|X]), na
análise verificamos se a relação causal entre uma variável econômica a ser explica-
da (variável dependente = Y) e uma ou mais variáveis independentes ou explicativas
(X) são válidas ou necessitam de mais aprofundamentos.
Na análise de regressão quando temos uma única variável independente ou ex-
plicativa, nós temos uma regressão simples e, quando temos mais de uma, o que
é muito comum nos estudos econométricos, temos a regressão múltipla. Mais à
frente veremos maiores detalhes destas duas formas de regressão.
Em toda a análise de regressão também se inclui o termo erro. Este termo tem por
objetivo ser a variável de ajuste de uma regressão que permite equilibrar a exatidão
das análises quantitativas com a inexatidão dos fatos econômicos de acordo com
a teoria econômica. Assim, o termo erro (aleatório) deve ser incluído na relação
exata postulada pela teoria econômica e economia matemática, a fim de torná-
las probabilísticas (isto é, a fim de refletir o fato que, no mundo real, as relações
econômicas entre as variáveis econômicas são inexatas, e algumas vezes erráticas).
1. Explique a ligação entre amostra, frequência e média.
2. Explique a diferença entre a econometria teórica e a
aplicada.

23. Conceitos introdutórios e especificação de modelos econométrico
U1
21
Seção 2
Conceito e classificação de modelos
Introdução à seção
Tendo em vista que os propósitos da Econometria envolvem mensurar variáveis por
meio da estimação de parâmetros, para que ela consiga cumprir estes propósitos
é necessário estabelecer alguma relação entre as variáveis para poder modelar
os dados coletados acerca destas variáveis. Neste sentido, torna-se importante
conhecer os conceitos que envolvem a compreensão do que é um modelo, e é
isto que vamos estudar nesta seção.
2.1 Modelo: conceito e tipos
Um entendimento mais geral sobre o que vem a ser um modelo permite dizer
que ele é constituído de uma representação simplificada da realidade que
contemple uma montagem estruturada de tal forma que permita compreender o
funcionamento total ou parcial da realidade observada.
De outro modo, um modelo pode ser uma representação abstrata da realidade da
qual se separa apenas o que é relevante para a análise proposta, negligenciando
todos os demais aspectos. É importante saber que não existe um modelo capaz
de expressar completamente a realidade, portanto, os modelos sempre serão
passíveis de alterações e mesmo assim serão incompletos.
Por outro lado, os modelos buscam fazer uma representação formal de ideias
ou conhecimentos acerca de um fenômeno (que é uma parte da realidade
observada). As ideias ou teorias são formadas por um conjunto de hipóteses
“sobre os elementos essenciais do fenômeno e das leis que o regem, as quais
geralmente se traduzem sob a forma de um sistema de equações matemáticas”
(MATOS, 1995 p. 20).

24. Conceitos introdutórios e especificação de modelos econométrico
U1
22
As hipóteses constituem-se no uso da teoria existente a priori para se certificar
como poderia evoluir um fenômeno econômico. Assim, quando observamos que
preço e quantidade variam em direção oposta para explicar a demanda utilizamos
a hipótese ceteris paribus, ou seja, supomos que todas as demais variáveis como
renda, preferência do consumidor se mantenham constante.
De modo geral, a existência de uma teoria e de hipóteses fundamentadas nelas é
uma racionalização fundamental para a construção de um modelo.
De uma maneira mais geral, os modelos econômicos podem ser classificados
em modelos teóricos ou econométricos. Os modelos teóricos são aqueles que
expressam leis econômicas sem conter uma especificação efetiva da forma
matemática nem a enumeração exaustiva das variáveis que o compõem. Por
exemplo, um modelo teórico da função demanda seria descrito como:
Qd = f(P)
Ceteris paribus ou caeteris paribus é uma expressão em latim que
significa “permanecendo constantes todas as demais variáveis”. Muito
utilizada em economia quando se deseja avaliar as consequências de
uma variável sobre outra, supondo-se as demais inalteradas.
Talracionalizaçãodemodelospermiteainvestigação
das consequências lógicas das hipóteses, consideradas
através de sua contrastação com os resultados da
experiência. Dessa forma, conhece-se melhor a
realidade e pode-se, em consequência, atuar, com
mais eficácia, sobre ela. Em síntese, a palavra modelo
refere-se a um conjunto de hipóteses estabelecidas
a priori sobre o comportamento de um fenômeno,
com base numa teoria já existente ou a partir de novas
proposições teóricas (MATOS, 2005, p. 20).

25. Conceitos introdutórios e especificação de modelos econométrico
U1
23
Que significa que a quantidade demanda (Qd) é uma função (f) do preço (P).
Já os modelos econométricos apresentam obrigatoriamente especificação
(forma matemática, definição das variáveis e número de equações) para aplicação
empírica, e ainda incorporaram um termo residual (erro aleatório) com a finalidade
de levar em conta as demais variáveis que influenciam o modelo, mas que não
está expressamente presente nele. Por exemplo, um modelo econométrico para a
função demanda pode ser descrito como:
Qd = a - bP + u
Na qual o máximo que o consumidor demandaria do produto é a (também
chamada de intercepto da função, isto é, se P=0 esta seria a demanda máxima),
e b representa o quanto o preço (P) influencia a demanda e u é o termo erro que
visa captar o efeito de todas as outras variáveis que influenciam a demanda (como
a renda e a preferência do consumidor), mas que não aparecem na formulação
do modelo econométrico. O Quadro 1.1 traz outros exemplos de modelos
econométricos formulados com base na teoria econômica.
No Quadro 1.1, M = meios de pagamento, i = taxa de juros, Y = renda e C =
consumo a e b0 são interceptos, b é a inclinação e os termos u e e são termo erro
aleatório. Desta forma sobre os modelos econométricos podemos concluir que:
Quadro 1.1 – Modelos econômicos e econométricos
Fonte: Adaptado de Matos (1995, p. 21)
Função Modelo
econômico
Modelo
econométrico
Teoria
econômica
Função liquidez M=L (i,Y) M = a + bi + cY+ u Teoria keynesiana
de moeda
Função
consumo
C = b0 + bY C = b0 + bY + e Função consumo
keynesiana

26. Conceitos introdutórios e especificação de modelos econométrico
U1
24
2.1.1 Estrutura de modelos econométricos
Segundo Matos (1995), os modelos econométricos prescindem de quatro
elementos básicos, são eles:
I) As variáveis são os entes sobre os quais serão coletadas as observações ou valores
que vão dar origem ao banco de dados e que podem apresentar diferentes valores.
Conforme vimos anteriormente, as variáveis podem ser dependentes (também
chamadas de explicadas, endógenas) ou independentes (também chamadas
explicativas, exógenas) que são aquelas que afetam a variável dependente. O
conjunto de variáveis explicativas mais o termo constante são denominados
costumeiramente de regressores.
II) As relações ou equações descrevem o comportamento que se espera das
variáveis observadas tendo em vista os elementos singulares de um fenômeno
econômico. Estas relações refletem a forma como as variáveis independentes
afetam as variáveis dependentes, e sempre será necessário estabelecer esta relação
considerando questões de diferentes ordens que unem tais variáveis (dependentes
e independentes num mesmo modelo). Estas relações podem ser:
Os modelos econométricos, embora contenham
os elementos que permitem sua operacionalização,
constituem uma formulação incompleta da realidade,
posto que se tem de recorrer à cláusula ceteris
paribus para preencher a lacuna entre a teoria e os
fatos. Isso ocorre em face da impossibilidade de um
modelo abranger todos os fatores que determinam
ou condicionam um fenômeno. Contrastando com
os modelos determinísticos que supõem a existência
de variáveis que satisfazem exatamente as equações
matemáticas, os modelos econométricos ou
probabilísticos não admitem relações exatas em virtude
da não inclusão de todas as variáveis que determinam
o comportamento do fenômeno e de erros de medidas
das variáveis (MATOS, 1995, p. 21).
a - Relações de comportamento – expressam ações
ou condutas dos agentes econômicos. Exemplo: (1)
Equação de demanda; (2) Equação de oferta.

27. Conceitos introdutórios e especificação de modelos econométrico
U1
25
III) A possibilidade de apurar os parâmetros ou coeficientes da regressão. Os
parâmetros expressam uma quantidade (número) que permanece constante em
determinado contexto, também chamado de termo constante. Este termo indica
a ausência de variações significativas na variável dependente ao longo do tempo.
Por exemplo, na equação Qo = a + bP, onde P e Qo são variáveis e a e b são
constantes, a e b são os parâmetros (SANDRONI, 1999).
IV) O termo erro ou perturbação expressa um grande número de pequenas
causas, que produzem um desvio em relação ao que a variável dependente
deveria ser, se a relação expressa pela equação econométrica estabelecida fosse
determinística. Desta forma, o termo erro tem uma série de significados que
podem surgir devido à: existência de variáveis omitidas; imprevisibilidade do
comportamento humano; variação do comportamento entre indivíduos; erros
de medidas da variável dependente; e especificação imperfeita das relações. “Tal
termo tem, pois, a finalidade de preencher a lacuna entre a teoria e os fatos.
Dessa forma, os modelos econômicos serão necessariamente não exatos ou
estocásticos” (MATOS, 1995, p. 23).
Depoisdeestabelecidosositensquecompõemaestruturadomodeloéinteressante
prosseguir apresentando as classificações dos modelos. Vamos estudá-los agora.
2.1.2 Classificações mais comuns de modelos econométricos
Os modelos podem ser classificados de acordo com a função ou com as
características do fenômeno econômico que se deseja modelar. Lembrando
b - Relações institucionais ou legais – refletem efeitos
provocados na atividade econômica por leis e normas,
isto é, descrevem o impacto do ordenamento jurídico.
Exemplo: Imposto sobre Circulação de Mercadorias e
Serviços como função do faturamento.
c - Relações técnicas – refletem ou expressam as
condições do processo de fabricação ou produção.
Exemplo: função de produção.
d - Relações contábeis ou definições – expressam
identidades entre magnitudes econômicas. Exemplos:
(1) Lucro = Receita – Custo (2) Patrimônio líquido =
Ativo real – Passivo real e (3) Y = C + I + G + X - M.
(MATOS, 1995, p. 22).

28. Conceitos introdutórios e especificação de modelos econométrico
U1
26
que as classificações não são excludentes e é fundamental entender a teoria
que fundamenta a construção do modelo. Vamos ver quais são as principais
classificações apresentadas por Matos (1995).
a - quanto à forma funcional: isto é, como se descreve a relação existente entre a
variável dependente e independente em termos de evolução delas na medida em
que aumenta o número de observações.
• Lineares – aqueles que são expressos por funções lineares (vide os tipos
de funções no Quadro 1.1). Exemplos:
(1) Y = a + bX
(2) Y = b0 + b1V + b2W
• Não lineares – aqueles expressos por funções não lineares (vide os tipos
de funções no Quadro 1). Exemplos:
(1) Y = a . Xb
(2) Y = a + b .1/x
b - quanto ao número de equações: isto é, quantas equações compõem o
processo que descreve a relação entre as variáveis.
• uniequacionais - contêm apenas uma equação. Exemplo:
W = a + bX + cY
• Multiequacionais – contêm, pelo menos, duas equações. Exemplo:
Y = a + bF + cP
Q = d + fP + gU
Y = Q
c - quanto à associação das variáveis com o tempo: isto é, se estamos observando
as variáveis considerando o mesmo tempo ou ao longo do tempo.
• Estáticos – quando o ajustamento da variável dependente em função do
efeito da variável explicativa ocorre simultaneamente no mesmo período de
tempo (Cross Section). Exemplo:
Qt = a + bPt + cWt
• Dinâmicos – quando as variáveis se referem a períodos de tempo
diferentes. Exemplo: Qt = a + bPt - 1 + cWt, onde a quantidade Q de um
produto em t é função de seu preço de mercado P em t - 1 e do índice
pluviométrico W em t.

29. Conceitos introdutórios e especificação de modelos econométrico
U1
27
d - quanto à finalidade: isto é para que se constrói o modelo.
• Modelos de decisão são aqueles orientados para o processo de tomada
de decisões.
• Modelo de previsão, que visam à previsão de valores de uma variável.
2.1.3 Modelos econométricos e suas qualidades
O bom econometrista não pode defender o uso de modelos de maneira arbitrária.
Assim, a utilização de modelos deve levar em conta as qualidades de um modelo
econométrico. Matos (1995) destaca algumas destas qualidades conforme as
descrevemos a seguir.
a - Plausibilidade teórica: espera-se que um modelo seja compatível com os
postulados da teoria econômica, isto é, deve descrever e explicar adequadamente
o fenômeno sob análise. Em especial, deve-se ter em mente que o fato da
variável dependente do modelo estar atrelado a variáveis independentes à relação
estabelecida entre elas é fundamentada na teoria econômica, embora a relação
possa ser estabelecida depois da coleta e, estudo dos dados, esta fundamentação
não pode deixar de existir.
b - Capacidade explanatória: espera-se que o modelo seja capaz de explicar os
dados observados, cuja relação ele determina. Podemos dizer que é necessário
que depois de estimados os resultados, encontremos uma relação possível do
ponto de vista quantitativo.
c - Exatidão das estimativas dos parâmetros: neste caso, os parâmetros estimados
pelo modelo deverão ser exatos no sentido de aproximar-se tanto quanto possível
dos verdadeiros parâmetros estruturais. Em especial, depois de estimados os
parâmetros, nós precisamos aplicá-los às observações que temos para ver o
quanto eles permitem aferir, a partir dos valores estimados, os verdadeiros valores
da variável dependente.
d - Capacidade de previsão: refere-se à capacidade do modelo de gerar previsões
satisfatórias de valores futuros da variável dependente. Neste caso, esta capacidade
torna-se mais confiável a partir do momento em que se aplica o modelo aos dados
passados e verificamos que os valores apurados se aproximam dos valores reais da
variável dependente, isto tornam mais confiáveis as projeções futuras.
e – Simplicidade: um bom modelo deve expressar as relações econômicas com
o máximo de simplicidade. Esta simplicidade pode ser expressa em termos de
número de equações e da forma matemática, ceteris paribus. Porém, deve-se
observar que as relações econômicas são fundamentadas em teorias com certo
grau de complexidade e é esta que confere a validade do modelo.

30. Conceitos introdutórios e especificação de modelos econométrico
U1
28
2.1.4 As etapas da modelagem econométrica
Figura1.2–Etapasdaconstruçãodemodeloseconométricos
Fonte: Matos (1995, p. 26).
sim
não
1ª Etapa:
Especificação ou
construção do
modelo
2ª Etapa:
Estimação
do modelo
especificado
3ª Etapa:
Avaliação da
equação estimada
Formulação
de hipóteses
Modelo
Matemático
Modelo
econômico
Coleta
de dados
apropriados
Estimação
dos
parâmetros
Avaliação dos
resultados
As hipóteses
são
aceitáveis?
Rejeição das
hipóteses
Revisão das
hipóteses
Desistência
das hipóteses
Previsão e/ou
decisões
Aceitação das
hipóteses
Teoria
econômica
Observação
do mundo
real

31. Conceitos introdutórios e especificação de modelos econométrico
U1
29
É importante reconhecer que a construção de um modelo econométrico não
pode surgir de uma vontade egocêntrica do pesquisador, mas que esta construção
deva ser movida por critérios e regras fundamentadas em uma teoria. Para que
se estabeleça um modelo econométrico é importante conhecer as etapas de
estruturação de um modelo.
Na Figura 1.2, você pôde conhecer um resumo esquemático das principais etapas.
Tal metodologia consiste basicamente em três etapas, quais sejam: especificação
do modelo, estimação do modelo especificado e avaliação da equação estimada.
Na primeira etapa, para especificar um modelo precisamos observar a realidade,
identificar um problema para o qual a análise possa ser feita utilizando-se da
modelagem econométrica. Depois, se verifica a teoria econômica que nos permita
fundamentar o problema, pois a partir disto poderemos formular as hipóteses.
Feito isto podemos construir um modelo econômico e, neste caso, também é
chamado de modelo matemático porque estabelece uma relação matemática
entre as variáveis observadas. Depois podemos transformá-lo num modelo
econométrico. Esta transformação ocorre com a incorporação do modelo geral
dos parâmetros e do termo erro aleatório, conforme vimos no Quadro 1.1.
Podemos citar alguns exemplos, tais como:
• Venda de calçados (C) em função (f) do preço (P) e dos gastos
promocionais (GP) => modelo matemático => C = f (P + GP) => estabelecer
o modelo econométrico => C = a + bP + c(GP) + e. No modelo
econométrico a, b e c são parâmetros a serem estimados e e é o termo erro
aleatório.
Outro exemplo seria:
• Vendas de tinta (T) é função (f) dos gastos promocionais (GP), preço (P) e
renda familiar disponível (RD) => modelo matemático => T = f (GP + P + RD)
=> estabelecimento do modelo econométrico => T = a + bGP + cP + dRD
+ e. No modelo econométrico a, b, c, d são parâmetros a serem estimados e
e é o termo erro aleatório.
Na segunda etapa vamos em busca dos dados necessários para a estimação
do modelo econométrico proposto. Segundo Gujarati (2011), a análise
econométrica depende de dados adequados e os dados podem ser de três
tipos: cortes transversais (cross section), séries temporais e dados combinados.

32. Conceitos introdutórios e especificação de modelos econométrico
U1
30
Os dados de corte transversal “consistem numa amostra na qual todas as unidades
são observadas num mesmo instante de tempo” (SCHRODER; PINA, 2012 p. 1)
são coletados observando-se as variáveis no mesmo tempo. Exemplos de dados
de corte transversal são: o censo demográfico cujo último feito no Brasil foi em
2010, dados da Pesquisa Nacional de Amostra por Domicílios (PNAD), para um
mesmo período. De fato, estas pesquisas podem ser feitas com certa periodicidade
(mensal, anual, etc.), mas quando utilizamos apenas um único período ou um
período intermediário destas pesquisas estamos utilizando dados cross section.
Dados de séries temporais constituem-se de um conjunto de observações dos
valores que uma variável assume em diferentes momentos do tempo. Esses
dados podem ser coletados em períodos, tais como: diariamente (ex.: preço de
ações); semanalmente (ex.: preços do CEASA); mensalmente (ex.: IPCA, IGP, taxa
de desemprego); trimestralmente (ex.: PIB); anualmente (ex.: orçamento público);
quinquenalmente e decenalmente (ex.: Censo Demográfico).
Os dados de séries combinadas unem informações de observação para diferentes
entidades em diferentes ao longo do tempo. Por exemplo, observar o PIB do Brasil,
Paraguai, Uruguai, Argentina e Venezuela no período de 2000-2010, isto resultará
na construção de uma tabela com 50 observações (5 países vezes 10 anos de
observação para cada país). Um tipo de dados de combinados utilizados é o que
chamamos de dados em painel no qual as unidades observadas são pesquisadas
dentro de um corte de tempo. Devido à característica deste livro de ser um material
introdutório, não será aprofundado o trabalho com séries temporais e dados em
painel. A maior parte dos exemplos e destaques deste livro limita-se a trabalhar
com dados cross section.
Em relação à fonte de dados, hoje, podemos encontrar dados disponibilizados
por instituições públicas de pesquisa na internet, destacando que os dados mais
utilizados por economistas são os dados não experimentais. Estes dados têm a
característica de não serem controlados, mas apenas coletados pelo pesquisador.
Podemos citar como exemplo: o PIB, as taxas de desemprego, inflação, taxa de
câmbio, preço das ações etc.
Você poderá estudar mais sobre dados e conceitos básicos desta
segunda etapa lendo o Capítulo 1, Tópico 1.1, do livro de Econometria,
de James H. Stock e Mark W. Watson, publicado em 2004 e disponível
na biblioteca digital Pearson.

33. Conceitos introdutórios e especificação de modelos econométrico
U1
31
Em relação à precisão dos dados utilizados, devemos fazer alguns alertas sobre a
qualidade de tais dados. Podem ocorrer erros na coleta de dados (experimentais
ou não), os dados econômicos são apresentados de maneira muito agregada
e a confidencialidade de alguns dados realmente impede a divulgação mais
desagregada deles, por exemplo, os dados da declaração do imposto de renda
quando divulgados são somente dados agregados para impedir o reconhecimento
de um único indivíduo. Portanto, sempre que se utilizar uma fonte de dados deve-
se conhecer sua abrangência e suas limitações e sempre que possível destacar
em nota as observações que possam levar a alguma dúvida sobre a natureza dos
dados utilizados para a realização de um estudo econométrico.
Outro aspecto importante em relação aos dados é a atenção que se deve dar
à escala de medição das variáveis, pois além das considerações matemáticas
normais tais como quantidade/peso (dados em ton. não podem ser misturados
com dados em kg; devem-se transformar os dados numa mesma unidade)
unidades com unidades (somar dados de unidades diferentes sem respeitar a regra
de transformação) também temos que observar a unidade de referência na coleta
dos dados.
Assim os dados podem ser gerados com escalas de razão, por exemplo, o PIB per
capita é uma razão que resulta da divisão do PIB pela população residente no país.
Quanto à escala de intervalo, você pode utilizar um intervalo de tempo, mas não
pode utilizar a razão entre dois intervalos, pois a análise ficaria sem sentido.
Existem variáveis com escala nominal como, por exemplo, gênero (masculino/
feminino) ou estado civil (casado/solteiro) elas apenas denotam categoria e não
podem ser apresentadas como nenhuma das demais escalas, mas podem assumir
valores que diferenciem, por exemplo, 1 se for masculino e 0 para feminino.
Neste caso teremos um dado meramente diferencial e que chamamos de variável
dummy, caso que estudaremos mais adiante.
Você conhece alguma base de dados pública?
Procure esta fonte e verifique as informações e como
elas estão disponíveis neste banco de dados.

34. Conceitos introdutórios e especificação de modelos econométrico
U1
32
Ainda na segunda etapa temos estimação dos parâmetros, de posse dos dados
o próximo passo é proceder ao cálculo dos parâmetros. A estimativa numérica
destes permite fornecer o conteúdo empírico ao modelo. A ferramenta através da
qual a econometria realiza a estimação dos parâmetros é a análise de regressão.
O termo regressão foi criado por Francis Galton, que constatou que a altura dos
pais poderia influenciar a altura dos filhos, porém todos regridem a uma média
populacional (conforme Gráfico 1.1); e Karl Pearson, que ao analisar grupos de
filhos de pais altos e baixos constatou que filhos de pais altos tendem a ser mais
baixos, e vice e versa, desta forma a altura deles sempre regride a uma média da
altura populacional. Mas a moderna descrição de regressão é:
Se aplicarmos este conceito ao estudo de Galton e Pearson, por exemplo, podemos
ver que a preocupação em prever a altura média dos filhos (variável dependente)
com base no conhecimento da altura dos pais (variável independente) poderia
ser expresso num diagrama (ou gráfico) de dispersão, conforme Figura 3. Neste
diagrama foram plotados a altura dos filhos, dada a altura fixa dos pais, verifica-se
que para cada altura dos pais os filhos podem ser mais altos ou mais baixos, porém
a média da altura dos filhos tende a elevar-se com a altura dos pais. Assim, se
conectarmos as médias de cada grupo, teremos uma linha de regressão, esta
espelha como a altura média dos filhos se eleva com a altura dos pais.
Esta linha de regressão traçada sem a estimação de parâmetros e obtida apenas
da plotagem dos dados observados em um diagrama de dispersão pode ser
definida como “linha que conecta o valor médio da variável dependente (altura dos
filhos) correspondente a um dado valor da variável exploratória (altura dos pais)”
(GUJARATI, 2011, p. 40).
A análise de regressão diz respeito ao estudo da
dependência de uma variável, a variável dependente,
em relação a uma ou mais variáveis, as variáveis
exploratórias, visando estimar e/ou prever o valor
médio (da população) da primeira em termos dos
valores conhecidos ou fixados (em amostragens
repetidas) das segundas (GUJARATI, 2011, p. 29).

35. Conceitos introdutórios e especificação de modelos econométrico
U1
33
Em termos econômicos a aplicabilidade da análise de regressão pode ser realizada
para diferentes problemas, podemos citar como exemplo: plotar o gasto com
consumo partindo da renda disponível, plotar a elasticidade preço da demanda
partindo dos preços e quantidades previamente conhecidos, plotar o desemprego
dados os níveis de salários nominais.
È importante destacar que em econometria a regressão consiste em “com base
em uma série de dados de duas ou mais variáveis, encontrar a equação que melhor
represente a relação entre elas” (VASCONCELLOS, 2000, p. 21).
É importante destacar que na regressão lidamos comum a relação estatística entre
variáveis com distribuição aleatória ou estocástica, isto é, que tem distribuição
probabilística. O sentido disto é dizer que no processo de estimação dos parâmetros
da relação entre variáveis (dependente e independente) não conseguiremos prever
com certeza o valor exato, apenas o valor estimado dos parâmetros e da variável
Figura 1.3 – Diagrama de dispersão
Fonte: Gujarati (2011, p. 40).

36. Conceitos introdutórios e especificação de modelos econométrico
U1
34
dependente. Por outro lado, quando uma relação é exata, ou seja, determinística,
e já se conhece esta relação não há porque encontrar valores estimados para tais
relações.
Outro aspecto importante é que embora na análise de regressão dispusemos sobre
variável dependente e independente, a ideia de causação, isto é, os resultados
dos parâmetros não permitem identificar se a variável dependente seja causa ou
consequência. Por exemplo, não se pode afirmar que as pessoas gastem mais
porque tem renda maior ou se elas gastam mais e procuram ter renda maior para
isto. O significado disto é que a relação de dependência não pode ser inferência
de causa. A causa deve ser buscada na teoria econômica, que fundamenta o que
causa o quê e por quê.
Outro aspecto importante é determinar o grau de associação entre a variável
dependente e independente, isto é, medir a correlação entre as variáveis. Na
análise de correlação procuramos identificar quanto uma variável está associada
linearmente à outra. O coeficiente de correlação mede a intensidade desta relação
linear. Aqui não importa a relação de dependência, pois as variáveis são tratadas
simetricamente, buscamos identificar a associação linear dos valores apresentados,
isto é, na correlação encontra-se um valor determinístico e não probabilístico.
Porém, aconselha-se, antes de iniciar qualquer processo de análise de regressão,
que se analise a correlação entre as variáveis e que uma correlação forte pode ser
um dos indícios de que teremos bons parâmetros estimados pela regressão.
Concluindo-se que na análise de regressão vamos estabelecer relações de
dependência entre as variáveis, mas não de causação, e que a correlação é
um indício de associação linear entre as variáveis estabelecida de maneira
determinística. A análise de regressão apresenta uma relação que é probabilística,
não determinística, aleatória e estocástica, palavras com significados diferentes
para pontuar que os valores da regressão são estimados, isto é, se aproximam de
um valor real. Por isto a regressão estima uma reta de valores estimados e que para
obtenção do verdadeiro valor da variável dependente terá que se acrescentar um
termo de erro, também aleatório.
Na terceira etapa vamos realizar a avaliação da equação estimada. O objetivo é
verificar a adequação dos parâmetros às hipóteses tanto do modelo quanto do
método escolhido. “Considerando que o modelo ajustado seja uma aproximação
razoavelmente de boa qualidade, é preciso desenvolver critérios adequados para
verificar se as estimativas obtidas, estão de acordo com a teoria que está sendo
testada” (GUJARATI, 1995, p. 31).

37. Conceitos introdutórios e especificação de modelos econométrico
U1
35
Em nossos estudos, o método mais utilizado será o de mínimos quadrados
ordinários e mais à frente conheceremos mais detalhes deste. No processo de
análise, eles devem passar pelo processo de inferência estatística, isto é, realizar-se-
ão os testes de hipóteses. As hipóteses referem-se tanto à teoria econômica quanto
aos pressupostos básicos do modelo de regressão linear por mínimos quadrados.
Os principais testes são: teste t, teste F, teste quiquadrado, cujos detalhes também
veremos mais à frente. Outros indicadores importantes do ajuste da equação são
o coeficiente de determinação (R2) e análise dos erros ou resíduos da regressão.
Caso, após o teste de hipótese, estes sejam aceitáveis, o modelo mostra-se
adequado à utilização para previsão ou auxiliar no processo de tomada de decisão.
Caso as hipóteses sejam rejeitadas, existem dois procedimentos que podem ser
tomados pelo pesquisador: revisão das hipóteses e teoria utilizada a priori ou
desistência das hipóteses.
No auxílio, a estimação de modelos por meio de regressões é hoje realizada em
sua maioria por softwares, tais como: R, SPSS, STATA, EWIEWS, SAS, MINITAB,
entre outros. Destes, o único disponibilizado gratuitamente é o R. Tendo em vista
a dimensão dos nossos estudos neste curso introdutório, não caberia ensinar a
utilização deste software que é demasiado complexo. Então em nosso livro vamos
utilizar, em muitos casos, a ferramenta de regressão do Excel, conforme vocês
viram também no livro e Métodos Quantitativos (Estatística).
Pois bem, depois de explorarmos os detalhes da construção do modelo
econométrico, nós vamos nos dedicar a aprofundar os estudos sobre as formas
apropriadas para especificar um modelo.
1. Explique o que se entende por modelo.

38. Conceitos introdutórios e especificação de modelos econométrico
U1
36

39. Conceitos introdutórios e especificação de modelos econométrico
U1
37
Seção 3
Especificação de modelos
Introdução à seção
É importante conhecer a fundo os passos para especificação do modelo. O
pesquisador deve dedicar um tempo maior à construção do modelo, pois a maioria
das dificuldades enfrentadas nas estimativas surge de erros na especificação do
modelo.
Neste sentido, nesta seção, você poderá compreender os passos para especificação
do modelo, bem como conhecerá as principais consequências de erros de
especificação.
3.1 Requisitos básicos de um modelo
A especificação do modelo nada mais é do que expressar a forma econométrica
de um modelo econômico. Naturalmente, a construção do modelo econômico
foi realizada com base na teoria econômica. Assim, a estrutura de tal modelo,
bem como as relações que se estabelecem entre as variáveis utilizadas, surge do
prévio conhecimento e esclarecimento por parte do pesquisador sobre a teoria
econômica que fundamenta suas escolhas. Desta forma, Matos (1995, p. 28)
adverte que:
Na especificação de um modelo, dever-se-ão
considerar, inicialmente, os seguintes requisitos:
a)Delimitaçãodofenômenoougrupodefenômenos
a ser estudado;
b) Identificação das variáveis;

40. Conceitos introdutórios e especificação de modelos econométrico
U1
38
Podemos expandir o entendimento da explicação de Matos (1995) descrevendo
melhor cada um dos requisitos e etapas do trabalho econométrico. No campo
da pesquisa, uma das questões mais difíceis de estabelecer de forma clara é a
delimitação do fenômeno a ser estudado o que requer, inicialmente, que se defina
o problema de pesquisa. Na metodologia e em técnicas de pesquisa, você já deve
ter lido algo sobre o problema de pesquisa.
De maneira geral, o problema é definido por meio de uma pergunta clara e objetiva
que requer estudos aprofundados para que se possa encontrar um resultado,
solução, arcabouço, reconstrução, enfim, é necessário conhecer o problema em
profundidade explorar seus aspectos e chegar a uma conclusão para o problema
proposto.
No caso da modelagem econométrica, se define o problema por meio de
uma pergunta que via de regra inclui como resposta prévia a necessidade de
mensuração de resultados, isto é, a busca de solução requer necessariamente o
uso de uma regressão. Então, vamos supor que tenhamos a seguinte questão:
quais os determinantes da demanda de leite tipo C, no município de Londrina,
entre 1990-2000?
O que é um problema de pesquisa?
c) Estabelecimento das relações entre as variáveis;
d) Definição da finalidade do modelo, a fim de
orientar a especificação da forma matemática, a
seleção de variáveis e o número de equações.
Em consequência, a especificação é a etapa
do trabalho econométrico que envolve: (a) a
determinação das variáveis dependentes e explicativas
a serem incluídas no modelo; (b) a expectativa a
priori dos sinais e da magnitude dos parâmetros; (c)
a forma funcional (linear ou não linear); (d) o número
de equações; e (e) forma de mensuração das variáveis,
como unidades adotadas, defasagens ou avanços de
efeitos de variáveis temporais, etc.

41. Conceitos introdutórios e especificação de modelos econométrico
U1
39
Nesta pergunta conseguimos delimitar o tema de estudo: demanda de leite;
especificação do tema: leite tipo C; o local que estamos observando e do qual
extrairemos os dados: em Londrina; e o período de estudo: entre 1990-2000.
No processo de identificação das variáveis, a teoria desempenha um papel
importante, pois como toda pesquisa requer uma revisão de literatura, isto é, que
o pesquisador leia o que já foi produzido sobre o tema para a partir daí elencar
as variáveis que farão parte de seu estudo. Depois de apresentar as variáveis que
são justificáveis pela teoria e pesquisas anteriores, o pesquisador poderá propor
a inclusão de novas variáveis justificando a presença de cada uma delas em seu
estudo.
Continuando com nosso exemplo, os estudos sobre demanda (D) de leite informam
que ela pode ser influenciada pelo preço (P) do leite (lei geral da demanda), pela
renda (R) dos consumidores e pelo gosto (G) ou preferência. E nosso conhecimento
sobre o município de Londrina nos permitiria incluir outra variável a localização (L)
ou bairro.
O próximo passo seria descrever a relação esperada entre a variável dependente
e as variáveis independentes. Nossa variável dependente é a demanda de leite
(D) e as demais seriam as variáveis independentes (P, R, G, L). Em nosso exemplo,
elas teriam a seguinte relação com a demanda: quanto maior o preço menor a
demanda, quanto maior a renda maior a demanda, quanto mais o consumidor
gostar de leite maior a demanda e quanto mais próximo ao centro, como ideia
de melhor localização, maior a demanda por leite. Desta forma, a finalidade deste
modelo será estimar a demanda de leite no município de Londrina.
A descrição da relação entre as variáveis permite especificar a forma matemática da
relação entre elas, desta forma, nós teríamos um modelo matemático representado
por:
D = - P + R + G + L
E finalmente relação estabelecida é de uma função linear e ao incluirmos o termo
de erro (também chamado resíduo) adicionando os parâmetros a serem estimados
teremos o modelo econométrico, de tal forma que:
D = b0
– b1
P + b2
R + b3
G + b4
L + u
b0
= Intercepto
b1
.... b4
= parâmetros das variáveis independentes
u = termo erro ou resíduo aleatório.

42. Conceitos introdutórios e especificação de modelos econométrico
U1
40
Neste sentido é importante conhecer as principais fontes de informações às quais
o pesquisador pode recorrer para dar subsídios à construção de um modelo.
3.2 Fontes de informações necessárias à especificação de modelos
Podemos citar como principais fontes de informação para construção do modelo:
i) a teoria econômica, estudos anteriores, ii) conhecimento sobre as condições
específicas do fenômeno e iii) o termo erro aleatório.
Na Teoria Econômica, buscamos conhecer os elementos necessários para
entender os pontos relevantes e que permitam identificar de maneira clara o
fenômeno observado, destacando a variável dependente e a independente, bem
como fundamentando a relação entre elas.
Na maioria dos modelos que usam a denominação
'econométrico' existe, em geral, uma combinação de
coeficientes livremente calculados por via dos dados
disponíveis e outros que são fixados, pressupostos
ou restritos, devido a limitações relativamente à
quantidade e qualidade dos dados de uma amostra.
Estas restrições ou pressupostos podem, muitas vezes,
ser feitos de acordo com a teoria econômica, ou usam,
por vezes, resultados de outras amostras / bases de
dados, esperando que os mecanismos econômicos se
apliquem de forma similar.
É muito importante que o pesquisador tenha
em mente que as definições dos elementos e da
relação entre eles surgem da teoria e das pesquisas e
constituem as hipóteses estabelecidas. Estas hipóteses
são reunidas num modelo e estarão sujeitas a posterior
confrontação com as informações fornecidas por
dados amostrais. Essa confrontação pode resultar em
concordância total, parcial ou mesmo discordância
total (MATOS, 1995).

43. Conceitos introdutórios e especificação de modelos econométrico
U1
41
No nosso exemplo da demanda do leite, a Lei da Demanda e os determinantes
da demanda são analisados e nos permitem identificar as variáveis relevantes, e
contribuem para se estabelecer quais determinantes são relevantes e como seria,
num primeiro momento, a relação entre as variáveis.
Os estudos anteriores reforçam os determinantes previamente estabelecidos na
teoria econômica, assim como, permitem acrescentar e vislumbrar mais variáveis
que permitam enriquecer o modelo, explorando outros aspectos não pensados no
momento inicial, mas que podem se mostrar originalmente.
Em nosso exemplo, quando acrescentamos a variável localização, esta poderia ter
surgido porque ao ler artigos científicos sobre o tema, é comum associar consumo
de um bem à localização. Destaca-se que “além de novas variáveis, informações
sobre efeitos defasados, formas funcionais, medidas, inter-relações entre as
magnitudes econômicas etc. podem ser sugeridas em estudos anteriormente
realizados” (MATOS, 1995, p. 29).
Existem estudos nos quais após extensa pesquisa o pesquisador detectou que a
abordagem de um fenômeno não contemplou algumas variáveis ou condições
adversas. Neste caso, as condições específicas de um fenômeno estudado podem
serincorporadasaomodelo.Nonossoexemplo,incluirnomodeloahereditariedade
do consumo de leite, ou seja, verificar se filhos de pais que consomem leite
consomem leite também como um dos determinantes da demanda de leite, no
município de Londrina, poderia ser esta a situação específica que não apareceu
nos estudos anteriores.
Pode-se dizer que, em termos de pesquisa científica, boa parte dos novos
conhecimentos é construída a partir de incrementos em pesquisas anteriores.
Estes incrementos surgem devido à existência de condições específicas que
necessitam ser investigadas e que podem constituir-se em fatores relevantes para
aperfeiçoamento das discussões sobre o fenômeno observado. Podem incluir
desde atualização de dados, aplicação de um experimento já realizado em uma
região para estudar outra região, testar novas formas funcionais para estudos já
realizados.
Por fim, todo modelo não é completo, isto é, não pode dar conta de explicar 100% da
realidade, aliás, ele é construído para ‘tentar’ explicar parte da realidade. Neste sentido
justifica-se a sua inclusão em todos os modelos do termo erro aleatório. Por outro
lado, deve-se destacar que um modelo deve explicar boa parte da realidade, indicando
que o termo erro engloba apenas os fatores menos relevantes para a explicação do
fenômeno. Os atores irrelevantes captados pelo termo erro não são incorporados ao
modelo em virtude da impossibilidade de medi-los ou de seu desconhecimento. Disto
conclui-se que o termo erro deve ser pequeno e ter pouca significância, pois, caso
contrário, teríamos um modelo com erros de especificação ou de medida.

44. Conceitos introdutórios e especificação de modelos econométrico
U1
42
Matos (1995) explicita um exemplo de especificação de modelo tomando por base
a teoria econômica sobre a demanda. Em seu modelo, a quantidade demanda de
um produto importado (Q) é uma função (f) do preço do bem (P), da existência
de bens complementares (C), do preço dos bens substitutos (S), da renda do
consumidor (Y), do gosto ou preferência (G).
Depois de realizar uma pesquisa em estudos anteriores, o modelo poderia
incorporar outras variáveis, tais como o volume de crédito disponível para aquisição
do produto (F) e o índice de distribuição de renda (D).
De posse do conhecimento da realidade que envolve o estudo, as condições
específicas do evento observado poderiam sugerir a inclusão das tarifas existentes
sobre o produto importado (T) e as restrições existentes para a importação do
produto (R). Por fim, o modelo incorporaria também o termo erro aleatório para
captar os efeitos de variáveis que afetam o modelo embora sejam desconhecidas
pelo pesquisador. Desta forma, o modelo seria expresso por:
Q = f (P, C, S, Y, G, F, D, T, R, u)
Um modelo matemático como este pode assumir a forma de uma função linear
e ser expresso por:
Q = b0 + b1P + b2C + b3S + b4Y + b5G + b6F + b7D + b8T + b9R + u
Neste modelo b0
é o intercepto, b1
... b9
parâmetros e u o termo erro. Então se
descreve como a teoria econômica permite também traçar a relação existente
entre a variável dependente de forma a expressar o sinal matemático desta relação.
Define-se agora, com base na teoria econômica ou
na observação direta da realidade, o sentido de variação
de cada variável explicativa. Isso é traduzido no modelo
pelo sinal associado a cada parâmetro. Se o efeito da
variável for direto, o sinal esperado será positivo. No
caso de impacto inversamente proporcional, esperar-
se-á sinal negativo. Ter-se-á sinal positivo ou negativo
(diferente de zero), na hipótese de efeito ambíguo,
ou seja, sentido de variação não definido a priori. A
direção do efeito, ou – o que é a mesma coisa – o sinal
do parâmetro, pode ser expressa pela derivada parcial
da variável dependente em relação a cada uma das
variáveis explicativas (MATOS, 1995, p. 30).

45. Conceitos introdutórios e especificação de modelos econométrico
U1
43
Então, de acordo com a teoria econômica, a expectativa é de que os parâmetros
da equação teriam os seguintes sinais:
δ = é a derivada matemática e segue as regras de derivação estudadas por você
na disciplina de Cálculo I. A relação entre as variáveis do modelo pode ser positiva
(>0) ou negativas (<0), sendo expressa na equação econométrica por sinais (+
ou -). Após esta fase de apresentação dos sinais esperados dos parâmetros da
equação, pode-se então apresentar o modelo econométrico conforme segue:
Q = b0 - b1P - b2C + b3S + b4Y + b5G + b6F + b7D - b8T - b9R + u
Perceba que os itens grifados na equação (b1, b2, b8 e b9) tiveram mudança de
sinal em relação ao modelo matemático, isto ocorreu porque identificamos que:
• De acordo com a teoria econômica, pela lei da demanda, se o preço (P)
do bem sobre a quantidade demandada (Q) diminui por isto - b1P.
• De acordo com a teoria econômica, se o preço dos bens complementares
(C) sobe, a quantidade demanda (Q) do bem principal reduz-se por isto - b2C.
• De acordo com estudos anteriores, levantou-se que os impostos sobre
importação (T) e as restrições existentes a importação do produto (R)
reduzem a quantidade demandada (D), por isto - b8T e - b9R.
Adverte-se que em geral não é indicado que um modelo incorpore muitas
variáveis explicativas, porque muitas delas terão, na prática, efeitos estatisticamente
desprezíveis e também haverá certa dificuldade em estimar os parâmetros e corrigir
os erros que possam surgir devido à violação dos pressupostos básicos de um
modelo, conforme veremos mais adiante.
Outra observação importante sobre os modelos é que eles podem ser construídos
previamente, porém deve-se sempre conhecer alguma teoria aplicável ao modelo
que o fundamente, pois a construção de modelos sem teoria pode apresentar
implicações tais como: a) elevado condicionamento à hipótese ceteris paribus; b)
descrição, mas não explicação do fenômeno e por fim c) esterilidade do modelo
à medida que não permite atuar sobre o curso do fenômeno estudado (MATOS,
1995).

46. Conceitos introdutórios e especificação de modelos econométrico
U1
44
3.3 A expressão matemática adequada ao modelo linear
Em econometria básica se exploram os modelos lineares, isto quer dizer que a
relação entre as variáveis deve ser expressa por uma função linear. Nos exemplos
anteriores, a relação linear expressava que quando as variáveis independentes
variam (aumentam ou reduzem) provocam alterações proporcionais na variável
dependente (aumento ou redução), ocorre que isto nem sempre representa a
realidade.
É necessário conhecer e realizar um estudo sobre a melhor forma de relação
matemática entre os valores das variáveis dependentes e cada uma das variáveis
independentes para verificar qual a melhor forma funcional para o modelo
matemático e, depois escolher a forma de linearizar tal modelo, pois em regressão
precisamos trabalhar com modelos que a relação entre os parâmetros seja linear.
Matos (1995) apresenta uma tabela com as principais formas linearizáveis conforme
podemos ver na Tabela 1.1.
Para cada uma destas formas funcionais deve-se observar o correto procedimento
de linearização da forma original, que é o que se descreve na terceira coluna do
Quadro 1.1. Também é importante verificar as restrições impostas à utilização da
forma. Estas funções e suas transformações também já são bem conhecidas por
você depois de ver os estudos da disciplina de Cálculo I. Em econometria, antes
de rodar qualquer regressão, você precisa definir qual delas é mais adequada, pois
você precisará carregar os dados já com a transformação linear.
Tabela 1.1 - Formas Funcionais convencionais
Fonte: Matos (1995, p. 32)

47. Conceitos introdutórios e especificação de modelos econométrico
U1
45
Em alguns softwares mais específicos para estudos econométricos, como Stata,
é possível realizar as transformações por comandos dentro do próprio programa,
não sendo necessária a transformação prévia dos dados. Porém, como o software
mais acessível e comum que utilizaremos é o Excel, que é uma planilha de cálculo,
carregar os dados já transformados em uma etapa anterior é indicado, pois ele não
tem esta transformação disponível por comandos, dentro da ferramenta de análise
de regressão que ele disponibiliza. Você pode ver a descrição gráfica das formas
funcionais na Figura 1.4.
Figura 1.4 – Formas funcionais
Você consegue se lembrar dos tipos de funções que
você estudou em Cálculo I?

48. Conceitos introdutórios e especificação de modelos econométrico
U1
46
Cada uma destas funções tem suas características e aplicabilidade na economia,
vamos conhecer um pouco sobre elas e suas aplicações.
A função logarítmica é muito utilizada na estimação de funções de produção e
de demanda.
Fonte: Adaptado de Matos (1995, p. 32-33).
No caso de funções de produção, torna-se possível
testar a existência ou não de retornos constantes,
crescentes ou decrescentes de escala do uso de algum
insumo. No que se refere a equações de demanda,
o uso da forma logarítmica permite o cálculo de

49. Conceitos introdutórios e especificação de modelos econométrico
U1
47
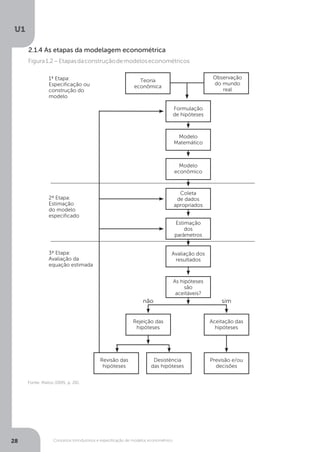
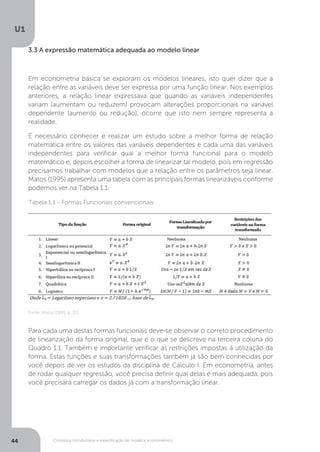
A função exponencial é utilizada para descrever processos de crescimento de
uma variável no tempo, de tal forma que:
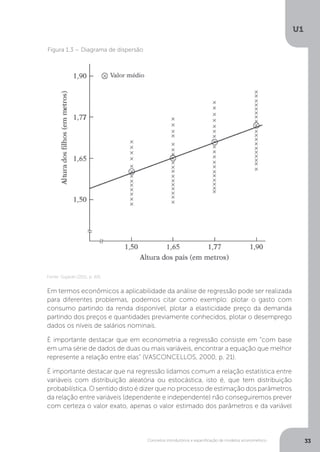
A função semilogarítmica II é utilizada quando estamos mensurando um efeito
sobre uma variável dependente na qual os acréscimos na variável independente
fazem a variável dependente crescer a taxas positivas, porém declinantes na medida
em que a variável independente aumenta. Exemplo econômico é o efeito Engel.
elasticidade constante. De modo geral, o uso de tal
função é adequado toda vez que uma variável cresce
com o aumento de outra, porém a taxas decrescentes
ou crescentes. Serviria, então, para captar o efeito Engel
da renda disponível sobre o consumo (crescimento a
taxas decrescentes) ou sobre a poupança (crescimento
a taxas crescentes) (MATOS, 1995, p. 32).
Particularmente, tem-se que LnY Lna Lnb.t, a
taxa de crescimento, g = (antiln b - 1) x 100. Pode-se
igualmente aplicar tal função quando uma variável
cresce (ou decresce) com os acréscimos de outra,
porém a taxas crescentes (decrescentes). [...] A restrição
é que a variável dependente assuma somente valores
positivos (MATOS, 1995, p. 34).
O efeito Engel pode ser aplicado sobre o consumo individual. Isto
implica que as taxas de variação das despesas individuais de consumo
de um dado bem são positivas, mas declinam com os acréscimos de
renda.

50. Conceitos introdutórios e especificação de modelos econométrico
U1
48
Na função hiperbólica ou recíproca, as variáveis podem assumir tanto valores
positivos quanto negativos. “Portanto, pode-se utilizar a função hiperbólica, quando
a relação entre as variáveis não for linear e estas assumirem valores diferentes de
zero” (MATOS, 1995, p. 34).
A função com forma quadrática é utilizada quando a relação entre as varáveis é
crescente, até certo ponto atinge um limite e depois se torna decrescente gerando
uma curva em formato de U ou também U invertido. Podemos citar, como exemplo,
a curva de custo marginal, a maximização dos lucros e maximização da utilidade.
A função na forma logística: Observe-se que, nessa função, se X +
8
, Y M.
Por outro lado, se X -
8
, Y 0.
Depois de compreendido um pouco sobre as formas funcionais, adverte-se que
em muitos casos pode ser indicada uma combinação de formas funcionais, porém
esta mescla deve estar amparada na teoria econômica.
3.4 Alguns critérios para auxiliar a escolha da forma funcional
No estudo introdutório de econometria, em que o estudante ainda conhece pouco
sobre todo o arcabouço teórico da economia, sugere-se que ele busque iniciar
seus estudos utilizando como base algum conhecimento teórico; reforçar este
conhecimento por meio de pesquisa bibliográfica; e que utilize artigos e pesquisas
anteriores como base. Seu processo de aprendizado sobre modelos pode passar
pela reprodução de resultados encontrados em estudos anteriores. Esta etapa é
importante para verificar o nível de conhecimento sobre o modelo econométrico
que se pretende utilizar.
Emfacedessascaracterísticas,talfunçãoé,emgeral,
utilizada na descrição do comportamento de variáveis
que começam a crescer vagarosamente, passando a
aumentar rapidamente e, finalmente, alcançam um
ponto de saturação M. Tal forma funcional é usada, por
exemplo, para descrever o crescimento demográfico
ou das vendas de um produto novo ao longo do tempo
(MATOS, 1995, p. 34).

51. Conceitos introdutórios e especificação de modelos econométrico
U1
49
Por outro lado, na medida em que avança em seus estudos, o pesquisador perceberá
que “a teoria econômica, em geral, informa muito pouco sobre a forma funcional
mais adequada a ser usada na especificação de um modelo econométrico.
Ademais, não existe nenhuma regra prática para a solução do problema”. (MATOS,
1995, p. 36).
Normalmente, a escolha de um modelo começa por uma pequena indicação da
teoria, segue-se a análise de dados e, ao verificar problemas com o modelo que é
apontado pelos testes (que veremos mais adiante), retoma-se a forma funcional,
verificando outras possibilidades além da testada. Também se recorre à inclusão
ou exclusão de variáveis. Matos (1995) sugere que se utilizem alguns critérios, tais
como:
a. Simplicidade – entre uma forma funcional simples
e uma complexa, tende-se a escolher a primeira, se
ambas explicam o fenômeno de modo igualmente
bem. A virtude da simplicidade é talvez a razão pela
qual muitos pesquisadores escolhem a forma linear.
b. Indicação da teoria econômica – como o objetivo
de um modelo econométrico é dar conteúdo empírico
às formulações teóricas, o uso de várias formas
funcionais e a escolha da que apresenta resultados mais
satisfatórios, mas sem uma justificativa teórica, poderá
resultar numa mensuração desprovida de significado
econômico, isto é, seria uma relação espúria, um mero
exercício estatístico e não uma análise econométrica.
c. Poder preditivo – na verdade, um modelo
econométrico não deve apenas sumariar um
fenômeno efetivo, mas também ser útil para previsões.
Isso significa que a forma funcional deve, pelo menos,
ajustar-se bem aos dados (MATOS, 1995, p. 36).

52. Conceitos introdutórios e especificação de modelos econométrico
U1
50
A solução de todos esses problemas ainda não é completamente dominada ou
possível dentro da econometria. Em alguns casos, os problemas são identificados
como: autocorrelação serial, heterocedasticidade e multicolinearidade, em outros
o problema é como realizar a mensuração de variáveis subjetivas.
De qualquer modo, o saldo é positivo, pois, ainda que inexistam plenas soluções, o
exame crítico dos problemas que persistem é fundamental. Isso é possível através
de testes, comparações, melhoria de dados etc. O importante é lançar luzes na
obscuridade.
3.5 Limitações da econometria
A econometria apresenta limitações, sobretudo por se tratar da mensuração de
relações em uma ciência social e cujos dados espelham algumas peculiaridades e
que não são possíveis de modelar corretamente. Assim as limitações podem surgir
de duas fontes específicas, conforme destaca Matos (1995, p. 48):
Seriam problemas de ordem estatística:
a) dificuldade de dar tratamento a alguns tipos de
modelos não lineares;
b) autocorrelação observada entre os termos
residuais;
c) erros de observações nas variáveis;
* amostras pequenas e/ou não representativas;
* intercorrelação entre as variáveis explicativas,
impedindo o pleno conhecimento da verdadeira
relação (multicolinearidade).
Do ponto de vista econômico, destacam-se os
seguintes obstáculos:
a) dificuldade de incorporar aos modelos fatores
subjetivos como atitudes, opiniões, expectativas,
intenções, gostos do consumidor etc.;
b) problema de classificação de variáveis em
endógenas e exógenas, ou seja, dificuldade de
estabelecer a direção do efeito das variáveis;
c) problema de especificação da teoria e dos erros.

53. Conceitos introdutórios e especificação de modelos econométrico
U1
51
1. Especifique quais são os requisitos básicos para compor um
modelo.
2. Explique alguns critérios relevantes para a escolha de um
modelo. Matos (1995) sugere que se utilizem alguns critérios,
tais como:
Nesta unidade, você estudou a econometria e a importância de
delimitar bem um modelo para que ele possa ser utilizado como
um método que auxilie na realização de pesquisas e no processo
de tomada de decisão. Compreendeu as dificuldades e limitações
na mensuração de resultados. Assim discutimos o conceito,
evolução e objetivos da econometria, bem como entendemos o
que é um modelo econométrico e um pouco sobre a análise de
regressão. Para finalizar estudamos as exigências e necessidades
da especificação de modelos econométricos.
Para aprofundar os conhecimentos discutidos nesta unidade,
você poderá continuar estudando lendo o Capítulo 1 – Questões
de Dados Econômicos, Capítulo 2 – Revisão de probabilidade e
o Capítulo 3 do livro Econometria, dos autores James H. Stock e
Mark W. Watson, publicado em 2004 e disponível na Biblioteca
Digital Pearson. Desejo-lhe bons estudos!

54. Conceitos introdutórios e especificação de modelos econométrico
U1
52
1. Explique o que é análise de regressão e dê um exemplo:
2. Apresente as diferentes formas de classificação de modelos:
3. Explique o que é cada um dos três tipos de dados que podem ser
utilizados na modelagem econométrica.
4. Explique os três critérios para escolha da forma funcional.
5. Vamos imaginar que você tenha recebido o seguinte modelo
matemático:
Y = C + I + G
E recebesse a informação sobre a relação da variável dependente (Y) em
relação às variáveis dependentes.
Y/ C = b1
> 0 Y/ I = b2
> 0 Y/ G = b3
> 0
Considerando os demais componentes de um modelo econométrico,
reescreva o modelo matemático em forma de modelo econométrico.

55. U1
53
Conceitos introdutórios e especificação de modelos econométrico
Referências
GUJARATI, D. N. Econometria básica. 5. ed. Porto Alegre: Macgraw Hill,
2011.
HILL, R. Carter. Econometria. 3. ed. São Paulo: Saraiva, 2010.
LANGE, O. Introdução à econometria. Rio de Janeiro: Fundo de Cultura,
1961.
MATOS, O. C. Econometria básica: teoria e aplicações. São Paulo: Atlas,
1995.
PINDYCK, R. S.; RUBINFELD, D. L. Econometria: modelos e previsões. Rio
de Janeiro: Elsevier, 2004.
SANDRONI , Paulo. Novíssimo Dicionário de Economia. São Paulo:
Editora Best Seller, 1999.
SCHRODER, B.; PINA, V. Econometria para concursos. Rio de Janeiro:
Elsevier, 2012.
VASCONCELLOS, Marco A. (orgs.). Manual de econometria: nível
intermediário. São Paulo: Atlas, 2000.

57. Unidade 2
MODELO LINEAR GERAL E
INCLUSÃO DE VARIÁVEIS
ESPECIAIS
Em que se apresentam os pressupostos do modelo de regressão linear
simples e as equações que permitem estimar os parâmetros.
Na qual se exploram os critérios adotados para a estimativa do modelo,
bem como se apresentam as estatísticas de avaliação.
Em que se aborda a extensão do MQO com a inclusão de mais variáveis
independentes (explicativas) no modelo, destacando a forma de
estimação de parâmetros.
Seção 1 | O método dos mínimos quadrados ordinários
(MQO)
Seção 2 | Avaliação de Modelos Estimados
Seção 3 | Modelo de Regressão Múltiplo
Objetivosdeaprendizagem:Nestaunidade,vocêserálevadoacompreender
o modelo de regressão linear simples e múltiplo, bem como a inclusão
de variáveis especiais para promover a melhor adequação do modelo
a situações especiais. Utilizaremos o Método dos Mínimos Quadrados
Ordinários (MQO) como instrumento básico da análise de regressão linear.
Neste sentido, para compreender melhor o MQO e como ele pode contribuir
para entender processos econômicos a partir da análise de regressão, nós
propomos que o estudo desta unidade seja composto de três seções, quais
sejam:
Regina Lúcia Sanches Malassise

58. Modelo linear geral e inclusão de variáveis especiais
U2
56

59. Modelo linear geral e inclusão de variáveis especiais
U2
57
Introdução à unidade
Conforme vimos na Unidade 1, a regressão linear é o método de estudo da
econometria, porém, para que seu uso conduza aos objetivos econômicos, qual
seja estimar parâmetros para mensurar a variável dependente partindo de dados
conhecidos da variável independente, ela precisa seguir alguns pressupostos básicos.
Estes pressupostos surgem da forma como é concebido o modelo de regressão
linear geral em econometria, que utiliza o Método dos Mínimos Quadrados Ordinários
(MQO). Através deste método se estima uma reta de regressão que contém os valores
estimados mais próximos possíveis dos valores reais da variável dependente.
Neste sentido, o MQO tem ampla utilização em estudos que necessitam de algum
grau de previsão, em termos estatísticos. Seu uso permite realizar um processo de
extrapolação.
Assim, em economia poderíamos estar interessados em entender a relação entre o
valor do dólar e as exportações; se o aumento do gasto com saúde pública reduz o
número de doentes; se a melhoria da qualificação da mão de obra levou a aumentos
salariais etc. Dando continuidade, vamos ao estudo desta unidade.

60. Modelo linear geral e inclusão de variáveis especiais
U2
58

61. Modelo linear geral e inclusão de variáveis especiais
U2
59
Seção 1
O método dos mínimos quadrados ordinários
(MQO)
Introdução à seção
Em estatística, o estudo da regressão linear ocorre depois de verificada a existência de
correlação linear entre duas variáveis, e a utilização da regressão objetiva traçar uma
reta unindo os pontos que apresentam os valores estimados da variável dependente
em relação à variável independente.
Ocorre que, depois de encontrados os valores, ainda existem diferenças entre o
valor estimado e o verdadeiro da variável dependente, e a variável de ajuste é o
termo erro (resíduo). A diferença entre os valores reais e os valores estimados pode
ser positiva e negativa, porém com números absolutos diferentes. Que os termos
de erro poderiam se anular, pois os valores positivos e negativos não se anulariam.
Para contornar tal problema adotou-se a técnica de elevar o resíduo ao quadrado,
assim pela regra matemática da exponenciação, todos os valores negativos se
tornariam positivos, desta forma a soma do quadrado da diferença entre cada um
dos valores estimados seria aproximadamente zero. E este é um dos primeiros
pressupostos ou hipóteses do MQO.
Assim, nesta seção, vamos desenvolver o modelo de regressão linear simples como
instrumento introdutório para compreender como podemos utilizar uma variável
para prever outra variável e para estudar a correlação, como uma medida da força
da associação entre duas variáveis.
1.1 A regressão linear
A análise de regressão aqui utilizada serve como instrumento para desenvolver um
modelo estatístico e para estimar um modelo de regressão simples – que utilizaria
uma única variável numérica independente (X), para prever a variável numérica
dependente (Y). De tal forma que:

62. Modelo linear geral e inclusão de variáveis especiais
U2
60
Toda relação expressa pela regressão simples pode ser visualizada na Figura 2.1
Queremos aproximar os dados do gráfico de
dispersão por meio de uma reta cuja equação é da
forma y = α + β ∙ x, onde α é chamado de coeficiente
linear da reta e β é chamado de coeficiente angular
da reta. Esses valores α e β são constantes e são eles
que a caracterizam: cada reta tem um valor para α e
um valor para β eixos. Para traçar a reta, vamos, então,
fornecendo valores para x (variável independente) e
encontrando um único y tal que y = α + β∙x.
Ícone – É importante lembrar que α e β são duas
letras gregas chamadas alfa e beta.
Voltemos, agora, para a nossa situação inicial e
vamos traçar uma reta que, aparentemente, aproxima-
se de todos os pontos observados da melhor maneira
possível (esse procedimento chama-se regressão
linear). Provavelmente, nenhum dos pontos (xi, yi)
da amostra pertence à reta, conforme você pode
observar. Assim, para cada xida amostra, teremos yi=
α + β · xi + εi, onde εi é o erro cometido – a distância
entre a reta e cada yi – também chamado de resíduo
(BRANDT. 1987, p. 155).
Fonte:A autora (2015)
Figura 2.1 – Esquema da regressão linear simples

63. Modelo linear geral e inclusão de variáveis especiais
U2
61
Apenas fazendo distinção, pois na Figura 2.1 utilizamos µi (normalmente associado
a erro populacional) para representar εi (normalmente associado a erro amostral),
que representa o termo erro (resíduo), o termo y^i representa o y estimado e o
termo α representa o intercepto, o β representa a inclinação da reta de regressão.
Também a equação expressa uma regressão simples que envolve a estimação de
Y (variável dependente) e X (variável independente).
Então o fundamento do uso da regressão está em encontrar valores estimados
para Yi(Y^i) tomando por base valores conhecidos de Xi. Quando traçamos a reta
de regressão estamos unindo os diversos Y^i, dado os valores de Xi, e a diferença
entre o Y^i e o Yi é o termo de erro ou resíduo.
Assim, a forma como estimamos Yi é que nos remete ao método dos mínimos
quadrados (MQO), que é o processo que descrevemos na sequência.
1.2 Método dos mínimos quadrados ordinários (MQO) e pressupostos do modelo
A análise de regressão é o método mais tradicional de trabalho na Econometria.
Segundo Vasconcellos, no Manual de Econometria (2000, p. 22), “a regressão
consiste em, com base numa série de dados de duas ou mais variáveis, encontrar
uma equação que represente a relação entre elas. Uma vez encontrada essa
equação, é possível então utilizá-la para fazer previsões a respeito dos valores de
uma das variáveis”. Por isso, muitas vezes, a análise de regressão é o dispositivo
usado para iniciar quase todas as pesquisas empíricas.
Um dos modelos mais conhecidos para fazer análise de regressão é o
Método dos Mínimos Quadrados (MQO) aplicados aos casos de regressão linear.
Este método estabelece uma regra sobre como podemos utilizar as observações
amostrais. Segundo Hill (2010, p. 58), no caso do MMQ, esta regra está centrada
no princípio dos mínimos quadrados “este princípio afirma que para ajustar uma
reta aos valores dos dados, devemos procurar a reta de tal forma que a soma dos
quadrados das distâncias verticais de cada ponto à reta seja a menor possível”. Para
seguir este princípio o modelo apresenta seus pressupostos básicos.
1.2.1 Pressupostos básicos do MQO
1 – Linearidade – O modelo especifica um relacionamento linear entre y e x1 .....
xk. Greene (2003) esclarece que no contexto da regressão, a linearidade se refere

64. Modelo linear geral e inclusão de variáveis especiais
U2
62
à maneira pela qual os parâmetros e as perturbações entram na equação, não
necessariamente à relação entre as variáveis. Então, afirma-se que a relação de
linearidade deve ser entre os parâmetros e não necessariamente entre as variáveis.
2 – Rank ou posto Completo: Não pode haver relacionamento linear perfeito entre
as variáveis independentes; o número de observações tem de ser no mínimo tão
grande quanto o número de parâmetros; as variáveis independentes têm de variar.
3 – Exogeneidade das variáveis independentes: E [εi | xj1, xj2. . . ,xjK ]= 0. Indica que o
valor esperado do termo erro εi da amostra não é uma função de qualquer uma das
variáveis independentes observadas. Isso significa que as variáveis independentes
não carregam informações úteis, ou que tenham peso, para a previsão de εi.
4 – Homocedasticidade e não autocorrelação: cada perturbação, εi tem a mesma
finita variância σ2, e é não correlacionado com todos os outros distúrbios, εj. Esta
suposição limita a generalidade do modelo.
5 – Exogeneidade na geração de dados: os dados no (xj1, xj2,..., XjK) podem ser
uma mistura de variáveis constantes e aleatórias. O processo de geração dos dados
opera externamente às suposições do modelo, isto é, independentemente do
processo que gera εi. Nota-se que isso amplia A3. A análise é feita condicionalmente
ao X observado.
6 – Distribuição normal: os resíduos são normalmente distribuídos: o modelo de
regressão linear, com todos os seus pressupostos, é a plataforma básica para a
construção de modelos em econometria.
De maneira similiar, porém um pouco mais sintética em termos de representação
simbólica, Matos (1995, p. 42-43) expressa que:
Esses pressupostos são os seguintes:
Aleatoriedade de ui
– A variável ui
é real e aleatória
ou randômica.
Média zero de ui
– A variável ui
tem média zero, isto
é, E(ui
)=0.
Homoscedasticidade – ui
tem variância constante,
ou seja, var(ui
)=E(ui
^2 )= σ^2,ondeσ=constante.
A variável u_i tem distribuição normal, isto é, ui
~
N(0,σ^2 ).

65. Modelo linear geral e inclusão de variáveis especiais
U2
63
Desta forma, a utilização do Método dos Mínimos Quadrados como ferramenta
para estimativa e previsão gerando estatísticas confiáveis a partir da equação
estimada dependerá da validade desse conjunto de pressupostos. Todavia, a
violação de alguns desses é uma questão de grau e não de natureza, pois sempre
ocorrerá de algum modo. O importante é avaliar-lhe a extensão.
1.2.2 As implicações da violação dos pressupostos
Mesmo assim ainda podemos perguntar quais seriam as implicações para o
modelo caso alguns destes pressupostos fossem violados. De acordo com Greene
(2003), a suposição de que xi e εi são não correlacionados é crucial para utilização
do MQO. Porém, existe uma série de aplicações na economia em que essa
suposição é insustentável. Exemplos incluem modelos contendo variáveis que são
medidas com erro e modelos mais dinâmicos, envolvendo expectativas. Sem esta
suposição, nenhuma das provas de consistência dadas acima se mantém; então os
MQO perdem sua atratividade como um estimador.
Ao perceber esta dificuldade o autor complementa dizendo que, existe um método
alternativo de estimação chamado método de Variáveis Instrumentais (VI). Supondo
que, no modelo clássico yi = x’jβ +εi, os K variáveis xi podem ser correlacionados
com εi. Supondo também que exista um conjunto de L variáveis zi, onde L é ao
menos tão grande quanto K, de tal forma que zi está correlacionada com xi, mas
não com εi. Não é possível estimar β consistentemente usando o estimador dos
Ausência de autocorrelação ou independência
serial dos ui
Isso significa que E(ui
uj
)= 0 para i≠j.
Independência entre ui
eXui
, ou seja, E(ui
Xi
)=0.
Nenhum erro de medida nosX’s – As variáveis
explicativas são medidas sem erros.
O modelo tem especificação correta – Isso significa
ausência de erro de especificação no sentido de que
apenas uma variável explicativa é suficiente para
expressar adequadamente o comportamento do
fenômeno, assim como a forma matemática (linear ou
não linear) é corretamente definida.

66. Modelo linear geral e inclusão de variáveis especiais
U2
64
mínimos quadrados. Mas é possível construir um estimador consistente de β
usando as relações assumidas entre zi, xi, e εi.
E no final o autor reconhece e elenca uma série de dados amostrais que dado as
suas particularidades não teriam no MMQ um melhor método de estimação para
seus parâmetros, tais como:
A) Painel de dados – examinando um modelo para despesas municipais na forma Sit
= f (Sit-1,...) + εi. Os distúrbios são assumidos para serem livremente correlacionados
entre períodos, então ambos Si,t-1 e εi,t, são correlacionados com εi,t-1. Segue que
eles estão correlacionados uns com os outros, o que significa que este modelo,
mesmo com uma especificação linear, não satisfaz os pressupostos do modelo
clássico. Os regressores e perturbações estão correlacionados.
B) Regressão Dinâmica – examinando uma variedade de modelos de séries de
tempo que sejam da forma yt = f(yt-1,...) + εt em que εt é autocorrelacionado
com os seus valores passados. Este processo é essencialmente o mesmo que
foi considerado anteriormente. Desde que os distúrbios são autocorrelacionados,
segue-se que a regressão dinâmica implica a correlação entre a perturbação e uma
variável do lado direito. Mais uma vez, os mínimos quadrados serão inconsistentes.
C) Função Consumo – Por construção, o modelo viola os pressupostos do modelo
clássico de regressão. A função renda nacional Y = C + investimento + gastos
governamentais + exportações líquidas. Embora ocorra uma relação exata entre
C de consumo, renda e Y, C = f (Y, ε), é ambíguo e é um candidato apropriado
para a modelagem, é evidente que o consumo (e, portanto, ε) é um dos principais
determinantes da Y. O modelo Ct = α + βYt + εt não se encaixa nas premissas
para o modelo clássico se Cov [Yt, εt] ≠ 0. Mas é razoável assumir (pelo menos por
agora) que εt é não correlacionado com os valores passados de C e Y. Assim, nesse
modelo, é possível considerar Yt-1 e CT-1, como variáveis instrumentais adequadas.
1.2.3 Os estimadores MQO são BLUE
Geralmente, os parâmetros estimados, através do MQO, são chamados melhores
estimadores lineares não tendenciosos dentro da classe dos estimadores possíveis,
também chamados BLUE. Wooldridge (2011) aborda o Teorema de Gauss-
Markov, que justifica o uso do método de MQO em vez de usar uma variedade de
estimadores concorrentes. Sob as hipóteses 1 a 5, o estimador de MQO bj para βj é
o melhor estimador linear não viesado (Best Linear Unbiased Estimator – BLUE). A
fim de formular o teorema, o autor diz que é preciso entender cada componente
da sigla “BLUE”.

67. Modelo linear geral e inclusão de variáveis especiais
U2
65
Assim destaca-se que um estimador se define como uma regra que pode ser
aplicada a qualquer amostra de dados para produzir uma estimativa. O termo
não viesado refere-se a um estimador, por exemplo bj, de βj
é um estimador não
viesado de βj
se E(bj
) = βj
para qualquer β0
, β1
..., βk
cuja dedução matemática,
conforme demonstrou Greene (2003), é dado como:
b = (X’X)-1 X’y
b = (X’X)-1 X’(Xβ + ε)
b = (X’X)-1 X’Xβ + (X’X)-1 X’ε
b = β + (X’X)-1 X’ε
E[b|X] = β + E[(X’X)-1 X’ε]
Assim, para qualquer conjunto de observações, o estimador de mínimos quadrados
tem esperança β. Além disso, através da média de b dos possíveis valores de X,
obtém-se a média incondicional de b que também é β.
Quanto ao termo linear refere-se a um estimador bj de βj é linear se, e somente se,
ele puder ser expresso como uma função linear dos dados da variável dependente.
E o significado de melhor para o teorema corrente, o melhor é definido como a
variância menor. Dados dois estimadores não viesados, deve-se preferir aquele
com a variância menor conforme demonstração matemática de Greene (2003),
que requer conhecimento de matrizes:
Seja b0
=Cy com C uma matriz k x n e b0
outro estimador linear não viesado de β.
Então, E[Cy | X] = E[(CXβ + Cε)|X] = β
Com y = Xβ + εeCX = I
Então existem muitos candidatos.
Por exemplo, as primeiras k linhas de X. Então,
C = [X0
-1
:0], em que X0
-1
é a inversa das k primeiras linhas de X.
A matriz de covariância pode ser obtida,
Var[b0
|X] = σ2
CC’, ou seja,

68. Modelo linear geral e inclusão de variáveis especiais
U2
66
b0
= Cy = C(Xβ + ε)
= CXβ + Cε b0
= β + Cε b0
– β = Cε
Com isso,
Var[b0
|X] = E[(b0
– β)( b0
– β)’|X] = E[Cεε’C|X]
Var[b0
|X] = σ2
CC’
Agora, seja
D = C – (X’X)-1X’ ouC = D + (X’X)-1X’
Além disso,
Dy = (C – (X’X)-1
X’)y = Cy – (X’X)-1
X’y = b0
– b
Voltando,
Var[b0|X] =σ2
CC’
= σ2
[(D + (X’X)-1X’)( D’ + X(X’X)-1
)]
= σ2
[(DD’ + DX(X’X)-1
+ (X’X)X’D’ + (X’X)-1
X’X(X’X)-1
)]
Mas, como = CX = I CX = DX + (X’X)-1
X’X DX = 0
Portanto,
Var[b0|X] = σ2
[DD’ + (X’X)-1
] = σ2
(X’X)-1
+ σ2
DD’
= var[b0
|X] = σ2
DD’
Então,
var[b0
|X] > var[b0
|X]
Assim, b é o melhor estimador linear não viesado de β, à medida que possui
variância mínima.
Portanto, sob as cinco hipóteses de Gauss-Markov, na classe dos estimadores
lineares não viesados, MQO tem a menor variância. MQO também é, sob as
hipóteses de Gauus-Markov, assintoticamente (para grandes amostras) eficiente
dentro de uma classe de estimadores.
1.3 A estimação do modelo por meio do MQO

69. Modelo linear geral e inclusão de variáveis especiais
U2
67
Conforme já verificamos anteriormente, estimar um modelo de regressão por
MQO, é buscar minimizar a soma dos desvios (erro ou resíduo) ao quadrado.
Ocorre que para realizar este cálculo precisamos seguir alguns passos e conhecer
as equações que nos permitam chegar aos valores dos parâmetros.
A primeira equação de um modelo é aquela definida a priori pela teoria econômica
que nos dá equação matemática e que depois de incorporado o termo erro nos
fornece a equação econométrica. Desta forma, a equação econométrica do
modelo linear simples, o qual só tem uma variável independente (explicativa) é
dada por:
Yi
=a+bXi
+ui
(i=1,2,…,n)
Como essa equação se refere à população (isto é, todo universo de dados sobre
as variáveis do modelo), implicando a impossibilidade de cálculo, temos que
trabalhar com valores amostrais. Neste caso, a equação a ser estimada recebe
acentos circunflexos que indicam que os valores encontrados para os parâmetros
foram calculados por estimativas dos valores populacionais, isto é, considerando
uma amostra, por isto são denominados de parâmetros estimados. Desta forma, a
equação com parâmetros a serem estimados é descrita como:
Na primeira notação temos indicando que a variável dependente é um
valor estimado, isto é, não é o valor absoluto de Y, partindo apenas dos valores
estimados dos parâmetros ( .)Na segunda notação, o Yi é o valor absoluto
de Y considerando que a partir dos valores estimados ( .) e acrescendo-se a
eles o termo erro (ei
) teremos o valor de Y absoluto. A estimativa dos erros mínimos
é dada por:
Para encontrar resíduos mínimos considerando todos os parâmetros temos que
realizar a seguinte operação:
Sendo SR = Soma do quadrado dos resíduos. Assim, derivando-se esta equação
em relação a ^
a e a ^
b , igualando-se essas derivadas a zero e reordenando-se os

70. Modelo linear geral e inclusão de variáveis especiais
U2
68
termos, obtém-se o seguinte sistema de equações.
Simplificando-se e ordenando-se os termos deste sistema de equações, obtém-se
o sistema de equações normais:
Resolvendo-se este sistema de equações normais para ^
a e ^
b , obtêm-se as
estimativas de mínimos quadrados dos parâmetros a e b:
Obtém-se, assim, a equação estimada ^
Y i
=^
a +b ^
b X, que melhor se aproxima da
verdadeira relação E(Y) = a + bX. O estimador de b pode, também, ser definido
pelas seguintes expressões:
Sendo que em ii a expressão indica que a estimativa de b é uma média ponderada
dos valores de Y, em que os pesos são:

71. Modelo linear geral e inclusão de variáveis especiais
U2
69
Existe ainda outro método que pode ser utilizado para estimar uma regressão,
este método é conhecido como Máxima Verossimilhança, porém, devido à
característica deste curso ser introdutório à econometria e também dado que o
método de regressão mais utilizado em economia é o MQO, este método não será
abordado aqui. Em Para Saber Mais segue indicação de leitura complementar para
aqueles que quiserem conhecer este método também.
1.3.1 Análise dos resíduos
Depois de obtida a equação estimada do modelo, podemos obter a estimativa ê do
termo aleatório. Esta estimativa é dada por ê = Y -^
Y . Este procedimento é indicado
porque nos fornece informações úteis para avaliação do modelo (MATOS, 1995).
As principais observações que podemos fazer com esta análise são:
A existência de Outliers: Pode ocorrer de identificarmos que os valores do Yi
ficarem muito distantes do ^
Y 1
. Isto ocorre porque as observações de X estão muito
distantes de
_
X . Neste caso em que as observações se comportam diferentemente
das demais, podemos associar esta diferença a acontecimentos ou características
específicos associados a essas unidades de observação. Graficamente um outliers
aparece na Figura 2.2.
O método da máxima verossimilhança consiste basicamente em
maximizar uma função dos parâmetros da distribuição, conhecida
como função de verossimilhança. O equacionamento para a
condição de máximo resulta em um sistema de igual número de
equações e incógnitas, cujas soluções produzem os estimadores de
máxima verossimilhança. Em resumo teremos tanta funções quantas
incógnitas (variáveis independentes) tivermos no modelo.
Links com sugestões de leitura sobre Máxima Verossimilhança:
<http://www.portalaction.com.br/confiabilidade/421-metodo-de-
maxima-verossimilhanca> acesso: 20 jul. 2015.
<http://www.portalaction.com.br/inferencia/34-estimadores-de-
maxima-verossimilhanca> acesso: 20 jul. 2015.
<http://www.galileu.esalq.usp.br/mostra_topico.php?cod=364>
<http://www.fep.up.pt/disciplinas/2E103/ml.pdf> acesso: 20 jul. 2015.

72. Modelo linear geral e inclusão de variáveis especiais
U2
70
b) A omissão de variáveis explicativas relevantes: quando o termo erro ou resíduo
se demonstra com valores muito elevados, considerando o fenômeno estudado,
isto pode indicar que variáveis importantes para entender o fenômeno foram
omitidas do modelo, sendo sua ausência espelhada num elevado termo erro.
c) Correlação entre os resíduos: se houver correlação entre os ui e uj, sendo i # j
estaremos violando o pressuposto de ausência de autocorrelação.
d) Variância não constante;
e) Distribuição não normal.
Os problemas verificados previamente na análise dos resíduos, constituem-se
em violação dos pressupostos básicos do modelo de regressão linear MQO, este
problema será abordado na Unidade 3.
Sobre o MQO com modelo linear simples, adverte-se que ele não é muito útil
para a análise de fenômenos complexos, isto é, dependentes de muitos fatores.
“A consequência disso é que os resíduos e os parâmetros estimados do modelo
refletirão todas as imperfeições decorrentes dos erros entre o modelo proposto e
a realidade” (MATOS, 1995 p. 46). Porém, é indicado como instrumental didático
que permite identificar e reconhecer o processo de estimação de parâmetros.
Fonte: A autora (2015).
Figura 2.2 – Dispersão normal e outlier

73. Modelo linear geral e inclusão de variáveis especiais
U2
71
1.3.2 Modelo linear simples: exemplo numérico
Adaptando o exemplo de 4.1 de Matos (1995) procedemos à estimação de um
modelo linear simples. Então, vejamos.
Considerando que os estimadores procurados são dados pelas equações:
Precisamos calcular as relações expressas por cada um dos componentes da
equação. Para seguir o raciocínio descrito antes vamos fazer com que Q = Y e T
= X. Agora por meio de uma tabela que pode ser calculada manualmente ou pode
ser criada no Excel, utilizando-se de seus recursos, vamos calcular.
Fonte: Matos (1995 p. 49)
Tabela 2.1 – Brasil – índice da quantidade demandada (Q) e da tarifa real média (T) de
energia elétrica (1996 = 100), 1981-1990

74. Modelo linear geral e inclusão de variáveis especiais
U2
72
Fonte: A autora (2015).
Tabela 2.2 – Cálculo Auxiliar
Retirando informações da Tabela 2 construída temos:
• n sendo o número de observações que é igual a 10 (período de 1981-
1990);
• ∑YX = 107006
• ∑Y∙∑X = 949 x 1148 = 1089452
• ∑X2
= 3483,60
• (∑X)2
= 1148 x 1148 = 1317904
•
_
Y = 949 / 10 = 94,9
•
_
X = 1148 /10 = 114,8
É importante que você compreenda de onde vem cada um dos valores da
equação que permite estimar os valores de a (alfa) e b (beta). O conhecimento da
forma como estes valores são construídos, embora ainda de maneira simplificada,
permite entender e descrever melhor o processo que envolve a estimação da
função. Agora já temos os elementos que podem ser substituídos na equação para
poder calcular os valores estimados.

75. Modelo linear geral e inclusão de variáveis especiais
U2
73
Resolução
a) Estimando os parâmetros da equação de demanda por energia elétrica, utilizando
o modelo linear. Realizamos este processo substituindo as informações retiradas
da tabela nas equações de a (alfa) e b (beta).
b) Apresentando a equação estimada que fica:
^
Y = 158,8092 – 0,5567 X
c) Calculando os resíduos da regressão: para isto utilizamos a equação de Y estimado
(^
Y ) e substituímos os valores de X para encontrarmos o ^
Y i
correspondente a cada
Xi
conforme podemos verificar na coluna 4 da Tabela 2.3. Depois calculamos o
termo erro pela fórmula ei
= Yi
- ^
Y i
cujos resultados apresentamos na coluna 5.
Fonte: A autora (2015).
Tabela 2.3 – Cálculo dos resíduos da regressão

76. Modelo linear geral e inclusão de variáveis especiais
U2
74
Interpretação inicial de resultados: Os resultados informam que existe um consumo
de energia elétrica que independe da tarifa expresso pelo alfa = 158,8092 e que
a medida em que a tarifa (X) aumenta há uma redução no consumo de energia
expresso por beta = – 0,5567. Na análise dos resíduos, os valores absolutos
(negativos ou positivos) do termo erro são considerados elevados de acordo com
os valores expressos por ei
= Yi
- ^
Y i
indicando que outras variáveis omitidas no
modelo podem ter efeito significativo para estimar a demanda por energia elétrica.
A sequência de sinais negativos (1981-86) e de positivos (1987-90) também reforça
este argumento. Conforme já destacamos é comum que modelos simples tenham
pouco poder de explicação e por isto se utilizam como uma ferramenta didática
de exposição do método.
Partindo desta exploração da regressão linear simples podemos, agora, explorar a
sistemática de avaliação de modelos na próxima seção.
Você saberia destacar outras variáveis que podem ser
determinantes da quantidade demanda de energia elétrica?
1. Explique o que é a importância do pressuposto da
linearidade.
2. Quais são as principais observações que se podem
fazer a partir da análise dos resíduos?

77. Modelo linear geral e inclusão de variáveis especiais
U2
75
Seção 2
Avaliação de modelos estimados
Introdução à seção
Neste ponto podemos nos perguntar: haveria como confiar no modelo estimado
para utilizá-lo para realizar previsões?
Pois bem, assim como é possível estruturar o modelo, existem testes, critérios
e estatísticas que nos permitem verificar se os estimadores calculados a partir
do modelo apresentam as qualidades desejáveis dos estimadores de Mínimos
Quadrados Ordinários. Caso atendam a estes requisitos de qualidade, então
o modelo e os parâmetros estimados por ele podem ser utilizados com certa
segurança no processo de previsão. Vamos conhecê-los nesta seção.
2.1 Qualidades desejáveis dos estimadores MQO
Conforme já destacamos, num modelo de regressão trabalhamos com variáveis
aleatórias, isto é, que envolvem relações não determinísticas. Assim, uma variável
aleatória é caracterizada por um ou mais parâmetros, que se deseja estimar
tomando por base uma amostra.
A fórmula é chamada de estimador, no caso estimador de mínimos quadrados, e
o valor gerado por este estimador é chamado de estimativa. Como a estimativa
surge de variáveis aleatórias, também o parâmetro estimado é aleatório e, portanto,
possui média e variância (MATOS, 1995).
Aliás, nós devemos nos atentar para os momentos das variáveis os quais para
o MQO se destacam a média, variância e desvio padrão. A média, a variância e
desvio padrão também já foram contemplados nos estudos de estatística. Você
sempre poderá revisar estes conteúdos para compreender melhor a econometria.
Segundo Matos (1995, p. 57), “toda variável aleatória é caracterizada por um ou
mais parâmetros, que se deseja estimar a partir de uma amostra”.

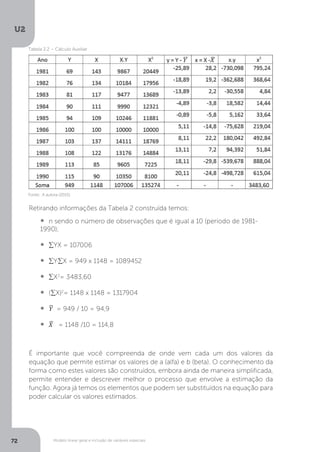
78. Modelo linear geral e inclusão de variáveis especiais
U2
76
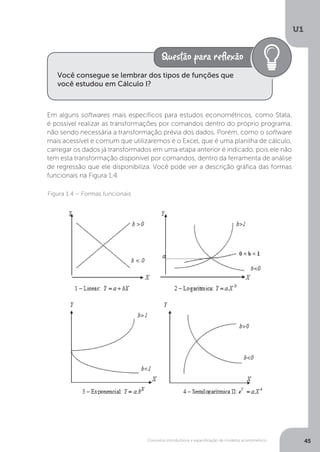
Em termos populacionais as variáveis aleatórias se caracterizam pelos momentos da
variável que em si são representados pelas seguintes medidas:
a) Média ou esperança matemática: E(q)
b) Variância: Var(q)=E[q-E(q)]2
=
=E(q2
)-[E(q)]2
c) Erro-padrão:EP(q)=√(Var(q) )
Em termos amostrais, as variáveis aleatórias se caracterizam pelos momentos da
variável que em si são representados pelas seguintes medidas:
a) Erro amostral: q-^
q
b) Tendenciosidade ou viés: E(^
q )-q
c) Erro quadrático médio (EQM): E(^
q -q)2
=Var(^
q )+[viés(^
q )]2
Matos (1995) destaca que: “É importante assinalar que, enquanto a variância mede a
dispersão em torno da média amostral, o erro quadrático médio mede a dispersão
em torno do verdadeiro valor do parâmetro q. Assim, se viés (^
q ) = 0, Var(^
q ) =EQM
(^
q )” (MATOS, 1995, p. 58).
Feitas estas considerações sobre os parâmetros, resta-nos acrescentar as qualidades
desejáveis dos estimadores MQO. Em especial, esta qualidade refere-se à capacidade
de se obter informações fidedignas possíveis sobre o valor do verdadeiro parâmetro, q.
Os momentos são muito importantes em estatística para caracterizar
distribuições de probabilidade. por exemplo, a distribuição normal é
caracterizada apenas pelo primeiro (média) e pelo segundo (variância)
momentos. Os momentos dão uma ideia da tendência central,
dispersão e assimetria de uma distribuição de probabilidades.
Isso significa dizer que o desejável é que a distribuição
dos valores de ^
q , obtidos a partir de amostras repetitivas,
seja o máximo possível concentradas em torno de q. Em
consequência, para se obter tal proximidade máxima,
a estimativa ^
q terá de possuir as qualidades de não
tendenciosidade, eficiência e consistência, que são
definidas a seguir (MATOS, 1995, p. 58).

79. Modelo linear geral e inclusão de variáveis especiais
U2
77
2.1.1 Não tendenciosidade
Um estimador é não tendencioso se sua distribuição amostral é igual à média dos
parâmetros estimados. Desta forma, “a estimativa ^
q de um parâmetro q, gerada
por um estimador qualquer, é não tendenciosa, se o valor esperado ou médio
de ^
q for igual a q. Em termos estatísticos, E(^
q ) = q.” (MATOS, 1995, p. 58). Logo
podemos ter q >^
q ou q <^
q , porém na média q = ^
q . Podemos verificar a relação
gráfica deste conceito observando a Figura 3.
2.1.2 Eficiência ou variância mínima
Um estimador eficiente tem variância mínima isto quer dizer que ele tem menor
dispersão em torno da média, ou seja, ele tem menor desvio padrão.
Na Figura 4 podemos verificar a representação gráfica da eficiência. Na linha cheia
que representa a f(^
q ) temos um estimador não tendencioso e eficiente. Na linha
pontilhada g(m~) temos um estimador não tendencioso, mas não eficiente devido
ao espraiamento da distribuição que aparece na base da curva ser maior que o
espraiamento de f(^
q ). Assim a opção seria pelo estimador f(^
q ).
Fonte: Adaptado de Matos (1995)
Figura 2.3 – Não tendenciosidade
Uma estimativa ^
q de q, obtida a partir de um
estimador qualquer, é eficiente ou tem variância mínima,
se as seguintes condições forem satisfeitas:
a) ^
q é uma estimativa não tendenciosa;
b) Var(^
q ) < Var (m~), onde m~ é uma estimativa obtida
mediante a utilização de outro estimador (MATOS, 1995,
p. 59).

80. Modelo linear geral e inclusão de variáveis especiais
U2
78
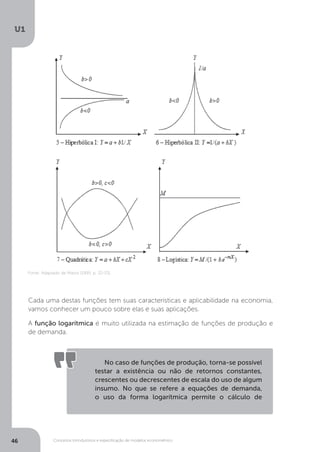
2.1.3 Consistência
Um estimador é consistente se sua distribuição amostral tender a se concentrar no
verdadeiro valor do parâmetro quando a amostra cresce. Então, uma estimativa ^
q
de q para ser consistente se o limite da probabilidade de ocorrência de ^
q for igual
a q de tal forma que:
Assinale-se que a diferença [E(^
q )-q]2
é o viés, ou seja, a distância entre E(^
q ) e o
verdadeiro valor do parâmetro, q. A representação gráfica da consistência pode ser
visualizada na Figura 2.5.
2.2 Critérios para avaliar as estimativas de um modelo
A segurança que podemos ter em utilizar um modelo econométrico para tomada
de decisão ou previsão deve ser pautada pela qualidade dos resultados obtidos.
Fonte: Adaptado de Matos (1995)
Fonte: Adaptado de Matos (1995)
Figura 2.4 - Eficiência
Figura 2.5 - Consistência

81. Modelo linear geral e inclusão de variáveis especiais
U2
79
Os critérios estabelecidos são de três origens diferentes: da teoria econômica,
critérios estatísticos e econométricos. A literatura sugere três critérios de avaliação.
Quanto aos critérios derivados da teoria econômica podemos comparar os
coeficientes bem como os sinais esperados para verificar se eles são condizentes
com a teoria econômica destacada a priori. Por exemplo, para uma equação de
demanda se estivermos utilizando os determinantes da demanda, em especial, o
preço do bem, nós podemos verificar se a lei da demanda se estabelece através da
indicação do sinal do parâmetro preço. Caso isto não ocorra, então teremos que
investigar o motivo desta divergência que poderia ser o fato de o produto ser ou
estar num momento em que se classificaria como bem de Giffen.
Especificamente, a avaliação da estimativa de um
modelo tem por objetivo verificar se os parâmetros
estimados são ou não teoricamente significativos e
estatisticamente satisfatórios ou confiáveis. Isso significa
verificar se a estimação do modelo formulado gera
uma equação empírica consistente ou de acordo com
as hipóteses estabelecidas a priori e, além disso, em
que medida os parâmetros dessa equação se afastam
das qualidades desejáveis de não tendenciosidade,
eficiência e consistência ou, em outras palavras, até
que ponto os pressupostos básicos do modelo são
violados ou não. Relembre-se que a violação de um
ou mais desses pressupostos compromete a validade
da equação estimada, ainda que seus parâmetros
sejam, eventualmente, consistentes com as hipóteses
formuladas aprioristicamente (MATOS, 1995, p. 61).
BEM DE GIFFEN. Um bem cuja demanda aumenta quando o seu preço sobe e
diminui quando seu preço desce, aparentemente contrariando a lei da demanda.
Essa forma de comportamento dos consumidores foi verificada por Robert
Giffen (1837-1910) ao observar as famílias mais pobres comprando mais pão à
medida que os preços deste produto iam aumentando. Isso acontece quando
a magnitude absoluta do efeito-renda (em relação aos preços) é maior do que
a magnitude negativa do efeito-substituição. Ou seja, embora mais caro, o pão
ainda é o produto mais barato, o que faz com que os consumidores deixem de
comprar outros produtos (mais caros) de sua dieta, para comprar mais pão. A
elasticidade – renda da demanda para um “bem de Giffen” é negativa.

82. Modelo linear geral e inclusão de variáveis especiais
U2
80
Matos argumenta que:
Quanto aos critérios estatísticos, eles permitem verificar a confiabilidade dos
estimadores por meio da realização da análise do coeficiente de correlação,
variância, desvio padrão determinação e testes de hipóteses realizados por meio
de estatísticas, tais como, teste t, teste F, teste quiquadradro. Todos eles foram alvo
dos estudos estatísticos, mas também serão relembrados aqui mais adiante.
Quanto aos critérios econométricos, seu objetivo é verificar se as estimativas
parâmetros possuem ou não as qualidades desejáveis dos estimadores, conforme
já destacado anteriormente.
2.2.1 Deduções matemáticas da média, variância e covariância
Dedução da Média e variância de ^
b :
Acontece, no entanto, que, por alguma razão, nem
sempre os sinais e a magnitude de um coeficiente
estimado estão de acordo com o que se espera a priori.
As possíveis razões para que isso ocorra são as seguintes:
a. Deficiência dos dados empíricos utilizados na
estimação;
b. Número de observações não adequadas em termos
de tamanho ou de representatividade do fenômeno que
se deseja analisar;
c. Violação de algum pressuposto básico do modelo.
Se os critérios não são satisfeitos, a estimativa é, em
geral, considerada insatisfatória (MATOS, 1995, p. 61).

83. Modelo linear geral e inclusão de variáveis especiais
U2
81
Como Y=a+bX+e , o valor de ^
b pode ser reescrito como segue:
Como ∑x=0 e∑xX=∑x2
, o valor de ^
b será:
Lembrando-se de que, por hipótese, E(e) = 0, conclui-se que:
E(^
b )= b
A variância de ^
b pode ser definida por:
, a variância de ^
b será:
No entanto,
Onde σ2
indica variância populacional de Xi
. Portanto:
Como Y=a+bX+e, tal expressão pode ser reescrita da seguinte forma:
Como ∑x=0 e ∑xX=∑x2
, tem-se, em consequência:

84. Modelo linear geral e inclusão de variáveis especiais
U2
82
Como E(e)=0, obtém-se a média de a:
E(^
a )=a
A variância da estimativa de a é definida por:
Covariância de ^
a e de ^
b
A covariância entre as estimativas de a de b é dada por:
2.3 Quadro de análise de variância
Compreender a decomposição da variância da variável dependente em especial
procurar compreender qual parte da variância pode ser atribuída à variável
independente e qual parte pode ser atribuída ao termo erro aleatório. Sendo a
variação total de Y (VT) definida pelo somatório dos desvios de Y em relação a sua
média, elevados ao quadrado, temos:

85. Modelo linear geral e inclusão de variáveis especiais
U2
83
Conforme explica Matos (1995, p. 66) destas deduções conclui-se que:
Estas definições podem ser sintetizadas na tabela da análise de regressão conforme
expressa na Tabela 2.4.
a) ∑y2
é a variação total de Y(VT) ou soma de quadrados
total (SQT).
b) ^
b ∑yxé a variação explicada por X (VE) ou soma de
quadrados da regressão (SQR).
c) ∑e^2é a variação residual (VR) ou soma de
quadrados residual (SQE).
Portanto, VT=VE+VR SQT=SQR+SQE
Tal soma indica que a variação dos valores de Y em
torno de sua média (VT) pode ser decomposta em duas
partes: uma que corresponde à variação de X(VE) e a
outra que expressa a variação residual ou não explicada
por X(VR). O valor de VR é atribuído ao fato de que os
pontos observados nem sempre pertencem à reta da
regressão devido a fatores omitidos ou aleatórios a que
estão sujeitas as variáveis econômicas.

86. Modelo linear geral e inclusão de variáveis especiais
U2
84
A partir da tabela de análise de variância podemos deduzir os demais elementos
importantes para a composição das estatísticas de avaliação, conforme segue:
Variância amostral: que mede o grau de dispersão entre os valores observados de
Y e o valor estimado (^
Y ). Dada pela fórmula:
Coeficiente de determinação (R2): É um coeficiente utilizado para demonstrar a
qualidade do ajustamento da linha de regressão, ou seja, “descobriremos quão
bem uma linha de regressão amostral é adequada aos dados... o coeficiente de
determinação é uma medida resumida que diz o quanto a linha de regressão
se ajusta aos dados” (GUJARATI, 2005, p. 65). Em termos de fórmulas pode-se
descrevê-lo como:
Quando realizamos a operação 1 – R2 podemos verificar qual parcela da variância
total de Y (VT) não pode ser explicada por X, devido à existência de variáveis
omitidas. Ele é descrito pela fórmula:
Tecnicamente ele mede a relação entre a variação explicada pela equação de
regressão múltipla e a variação total da variável dependente. Assim, R2=0,75
significa que 75% de variância são explicados pelo modelo. O coeficiente de
determinação (R2) é um número no intervalo [0;1], quanto mais próximo de um
melhor o ajuste.
Estatística de F: serve para avaliar o efeito conjunto das variáveis explicativas sobre
a variável dependente, ele é descrito pela fórmula
Fonte: Matos (1995, p. 67)
Tabela 2.4 – Análise de variância simples

87. Modelo linear geral e inclusão de variáveis especiais
U2
85
Estatística t: A estatística t testa a significância dos parâmetros estimados do
modelo, sendo calculada e apresentada para variável independente do modelo,
sua fórmula é expressa por:
modelo, sendo calculada e apresentada para variável independente do modelo,
Testeseanálisederesultados:AsestatísticasapuradaspelostestesteFsãoutilizadas
para confirmar ou não algumas hipóteses do modelo, conforme estudado em
estatística. Normalmente, as hipóteses são: “Hipótese nula (H0
), quando se admite
não haver diferença entre a informação fornecida pela realidade e a afirmação
da hipótese. Hipótese alternativa (H1
), quando se admite haver diferença entre a
informação fornecida pela realidade e a afirmação da hipótese”. (MATOS, 1995, p.
69). As regras de decisão para os testes são:
Teste F :
H0
: b = 0 (ausência de efeito da variável independente sobre a dependente).
H0
: b ≠ 0 (presença de efeito positivo ou negativo da variável independente sobre
a dependente).
Teste t:
Seguem-se os seguintes passos:
a) Escolhe-se o nível de significância (NS). E, geral, usam-se NS= 1%, NS = 5% ou
NS = 10%;
b) Verifica-se se o teste é unilateral (b>0 ou b<0) ou bilateral (b ≠ 0).
c) Verifica-se o valor crítico tc
na Tabela A.2, utilizando-se o nível de significância
(NS) adotado e o respectivo número de graus de liberdade (gl = n – k – 1).
d) Compara-se o t calculado com o tc
.
e) Regra de decisão.
• Se |t|>|tc
|, rejeita-se H0
(ausência de efeito), no nível de significância
adotado.
• Se |t|≤|tc
|, aceita-se H0
(ausência de efeito) no nível de significância
adotado.

88. Modelo linear geral e inclusão de variáveis especiais
U2
86
H0
:b=0 (ausência de efeito).
H1
:b>0 (presença de efeito positivo, de acordo com a teoria expressa no modelo
formulado).
Coeficiente de correlação (r): Indica o comportamento da relação entre Y e X,
esta relação é observada por meio dos desvios y e x, relembrando que os desvios
resultam da diferença entre o valor real e o valor médio da variável observada.
Então, o coeficiente de correção pode ser expresso como:
Matos (1995, p. 76) adverte que há diferenças importantes entre a correlação e a
regressão de tal forma que:
Pois bem, agora que conhecemos o modelo linear simples e as características
deste, bem como verificamos as formas de realizar avaliação de modelos, podemos
avançar para compreender o estudo do modelo linear geral com o qual podemos
incorporar mais de uma variável explicativa ao modelo.
A análise de regressão apresenta as seguintes
vantagens em relação à análise de correlação:
a. A regressão indica o sentido da relação de
dependência entre Y e X: Y X;
b. Os parâmetros que ligam as variáveis podem ser
estimados e utilizados em previsão, por pressupor um
mecanismo lógico de determinação de X sobre Y, no
caso da regressão, enquanto apenas se constata que as
variáveis se alteram de forma direta ou indireta, no caso
da correlação.
1. De acordo com Matos (1995) quais são as conclusões que
se podem tirar a partir da análise do quadro de variância?
2. Para que serve o coeficiente de determinação?

89. Modelo linear geral e inclusão de variáveis especiais
U2
87
Seção 3
Modelo de regressão múltiplo
Introdução à seção
O modelo de regressão linear geral também será estimado por MQO e tem
como vantagem a possibilidade de trabalhar com um número maior de variáveis
independentes.
Por outro lado, a possibilidade de ocorrerem problemas com as estimativas
também aumentam em decorrência de se trabalhar com mais variáveis.
Nesta seção, vamos explorar os detalhes da estimação múltipla, num primeiro
momento realizando a explicação dos cálculos envolvidos pelo processo abreviado
e manualmente e ao final da seção apresentaremos os itens mais relevantes, porém
utilizaremos as estimativas pelo Excel, como recurso computacional para explorar
alguns exemplos.
Adverte-se que o Excel não é o software mais apropriado para estas estimativas,
porém a realização de estimativas por outros softwares, como Stata, R, SPSS,
envolvem um nível de conhecimento e operação destes que fogem ao objetivo
deste livro introdutório de Econometria. O aluno que sentir necessidade poderá
procurar cursos específicos e aprofundar seus estudos nesta área.
3.1 O processo abreviado de estimativa do modelo geral
Primeiramente, precisamos relembrar que os pressupostos básicos do modelo
geral seguem os mesmos do modelo simples, já destacados anteriormente. Um
modelo de regressão linear geral pode ser expresso por:
Como ∑e é nula a equação em termos de média será:

90. Modelo linear geral e inclusão de variáveis especiais
U2
88
Subtraindo a segunda equação da primeira e reordenando os termos temos:
Esta é descrição do modelo linear geral em termos de desvios, assim reordenando
os termos temos:
SR = ∑e2
= ∑ (y – b1
x1
– b2
x2
- ... – bk
xk
)2
Depois de derivados e ordenados os termos, podemos verificar o sistema de
equações normais.
E reordenando em forma de sistema matricial temos:
O sistema fica: X’X . B = X’Y
Sendo: B = (X’X)-1
. X’Y
E o valor de ^
b o é dado por:
E o valor de b o é dado por:
Visando à compreensão deste processo,
é apresentado a seguir um exemplo
adaptado de Matos (1995), dando
prosseguimento ao estudo iniciado com
a tabela e acrescenta-se a coluna Y do
produto total.
Para maior compreensão deste
processo, vamos dar continuidade ao
estudo, com um exemplo adaptado de
Matos (1995) no qual se dá continuidade
aos estudos aqui iniciados com a Tabela
2.5 e acrescenta-se a coluna Y do
produto total.
Nota: A tarifa (T) foi deflacionada pelo índice geral de preços/
disponibilidade interna (Fundação Getúlio Vargas), enquanto
o produto (Y) foi corrigido pelo deflator implícito das contas
nacionais.
Fonte: Adaptado de Matos (1995, p. 92)
Tabela 2.5 - Índices da quantidade demandada energia
elétrica (Y), da tarifa real média (X1) e do produto real (X2),
1981-1990

91. Modelo linear geral e inclusão de variáveis especiais
U2
89
Em seguida, realizamos operações envolvendo matrizes a fim de estimar a
equação de demanda de energia elétrica por MQO múltipla. Considerando que
a resolução de matrizes foi estudada na disciplina de Matemática no Ensino
Médio, é importante para a compreensão do raciocínio desenvolvido, revisitar os
fundamentos da resolução de matrizes. Você também estudou um pouco disto na
disciplina de Cálculo/Matemática para Economista.
Inicialmente utilizamos o sistema matricial em pela forma de desvios:
Assim, obtendo a solução deste sistema considerando o raciocínio de que B=(X'
X)-1
∙ X'Y, tal solução possibilita-nos encontrar o valor de beta (B). A fórmula a seguir
permite a obtenção da estimativa do termo constante:
Para definir os elementos constantes do sistema matricial X^' X.B=X'Y procedemos
da seguinte maneira:
Seguindo os passos indicados, o sistema matricial é obtido ao tomar os dados
constantes da Tabela 4, representado por:
Assim, a matriz 2 x 2 é X’ X. Dando continuidade nos procedimentos para resolver
o sistema calcula-se a inversa, (X' X)-1
:
Cálculo do determinante D da matriz X'X
D=3.483,6 ∙854,1- [(-825,6)∙(-825,6)]=2.293.727,4
Cálculo da matriz cofatora C
C=[cij
]=(-1i+j
)∙Dij
Temos que Dij
é o determinante da submatriz que foi obtida depois da supressão
da i-ésima linha e da j-ésima coluna da matriz X'X. Considerando que, X'X é uma
matriz de segunda ordem, ou seja, (2 x 2), o escalar restante é o determinante da
submatriz, obtida após a supressão. Assim, obtemos a matriz cofatora:

92. Modelo linear geral e inclusão de variáveis especiais
U2
90
Para exemplificar como se realiza o cálculo dos elementos C_11 e C_12 da matriz
C, temos:
1. Cálculo da matriz adjunta A:
Na matriz adjunta, esta é correspondente à transposta da matriz cofatora. Dizemos
que A=C, pois tal matriz é simétrica.
2. Cálculo da matriz inversa
Ao solucionar o sistema de equações obtemos:
Os valores do vetor B são estimativas dos coeficientes das variáveis T e Y, obtidos
ao multiplicar a matriz inversa (X'X)-1
pelo vetor X'Y. Temos então:
Obtendo as estimativas de b1
e de b2
, podemos estimar b0
, o termo constante:
Chegamos então, a seguinte função de demanda estimada, utilizando três casas
decimais:
^
Q =7,778-0,263 T+1,238 Y
Procedemos à elaboração do quadro de análise de variância, com referência nos
dados amostrais e nas estimativas dos parâmetros. Vejamos na Tabela 2.6 a seguir:

93. Modelo linear geral e inclusão de variáveis especiais
U2
91
Fonte: Matos (1995, p. 96).
Tabela 2.6 - Análise de variância.
No qual temos que:
Dando continuidade aos estudos, temos o cálculo e interpretação da variância
residual.
Para obter a variância residual, utilizamos a seguinte fórmula:
Para realizar o cálculo e interpretação do coeficiente de determinação (R^2)
utilizamos a fórmula:
Observando a fórmula temos as duas variáveis explicativas, tarifa real (T) e produto
real (Y), que de acordo com o resultado obtido, significa que são responsáveis
por 93,1% da variação total da quantidade demandada (Q), de acordo com a
interpretação do coeficiente de determinação ou de explicação (R^2=0,931).
O R2
ajustado é dado pela fórmula:
Com os resultados obtidos, é possível realizar o cálculo da estatística F. Este cálculo
visa expressar qual é o efeito conjunto da tarifa real (T) e do produto real (Y) sobre Y.

94. Modelo linear geral e inclusão de variáveis especiais
U2
92
Utilizando-se a fórmula, obtém-se:
Obtêm-se os graus de liberdade do numerador igual a 2 e do denominador igual a
7 e o nível de significância definido foi de 5%, isto é, NS = 0,05. Portanto, apresenta-
se o valor crítico, fornecido pela Tabela de Distribuição F, é Fc
=4,74.
A hipótese que se deseja testar é verificar se as variáveis explicativas T e Y exercem
conjuntamente efeito significativo sobre a variável dependente Q. Tal hipótese é
expressa da seguinte maneira:
H0
:b1
=b2
=0 (ausência de efeito)
H1
:b1
≠b2
≠0 (presença de efeito)
a. Cálculo da estatística t e teste do efeito de cada variável explicativa
A fórmula a seguir corresponde ao cálculo da estatística t:
Por meio da aplicação dessa fórmula leva aos valores da estatística t para cada um
dos parâmetros associados aos X.
1. Estatística t para b1
=0
Para realizar o teste de significância do efeito da variável tarifa real (T) procedemos
à seguinte maneira:
H0
:b1
=0 (ausência de efeito)
H1
:b1
<0 (presença de efeito negativo, de acordo com a teoria)
Considerando o grau de liberdade igual a 7 e nível de significância de 5%, o valor
crítico de t para teste unilateral é tc
=1,895 (ou tc
=-1,895, por se tratar de teste de
efeito negativo).
Como |tc
|=1,895<|t|=2,91, rejeita-se a hipótese nula (H0
) em favor da hipótese
alternativa de efeito negativo, com um nível de significância de 5%.Tal resultado
indica que a influência da tarifa real (T) sobre a quantidade demandada (Q) é
estatisticamente significativa (diferente de zero), com uma probabilidade de erro
de 5%.

95. Modelo linear geral e inclusão de variáveis especiais
U2
93
2) Estatística t para b2
A seguir é apresentada a fórmula para a hipótese a ser testada:
H0
:b2
=0 (ausência de efeito)
H2
:b2
>0 (presença de efeito positivo)
Observe que o valor crítico é o mesmo obtido do teste anterior, permitindo assim,
concluir que, sendo |tc
|=1,895<|t|=6,78, a hipótese de efeito nulo H0
é rejeitada em
favor da presença de efeito positivo, ao nível de significância de 5%. A probabilidade
de erro é de 5% e tal resultado aponta que o efeito da variável produto real (Y) é
altamente significativo.
Uma colocação importante a ser feita, é que a estatística t para o termo constante
não pode ser calculada diretamente pelo processo abreviado.
b. Cálculo dos intervalos de confiança
Para calcular o intervalo de confiança parab_i utiliza-se a definição:
São considerados intervalos fechados. Assim, o valor crítico será tc
=2,365.
Consequentemente, os intervalos de confiança com 95% de probabilidade são
calculados da seguinte maneira:

96. Modelo linear geral e inclusão de variáveis especiais
U2
94
c.Análise dos resultados
Na realização dos resultados obtidos com a estimação do modelo, leva-se em
consideração o tamanho da amostra. São geralmente considerados o sinal e a
magnitude dos parâmetros, (critérios derivados da teoria econômica), assim como
as estatísticas de avaliação do grau de confiabilidade (coeficiente de determinação
e as estatísticas F e t), que são critérios de natureza estatística.
Vamos ver uma análise que envolve a função de demanda de energia elétrica.
Vejamos o seu desenvolvimento.
São consideradas uma amostra de 10 observações referentes ao período 1981/1990.
Os resultados obtidos com a estimação da função de demanda de energia elétrica,
são expressos da seguinte maneira:
Nesta situação, os resultados são satisfatórios, temos o coeficiente de determinação
(R2
) calculado e este indica que as variáveis tarifa real e produto real explicam 93,1%
da variação da quantidade demandada, tal resultado permite afirmar que tem alto
poder explicativo. Verificando por outro lado, a hipótese de efeito conjunto nulo é
rejeitada, ao nível de significância de 5%, conforme se verifica por meio do teste F.
Além disso, observa-se que os coeficientes estimados das variáveis tarifa e produto
real apresentaram sinais corretos, isto é, de acordo com a expectativa teórica aqui
estudada, e são considerados como estatisticamente significativos, ao nível de 5%.
Registre-se, em especial, o forte impacto do nível da atividade econômica, medido
pelo produto real, sobre o consumo da energia elétrica no Brasil no período
tomado como análise.
Para concluir, com a ressalva quanto ao pequeno tamanho da amostra (n = 10),
os coeficientes de elasticidade-tarifa (0,318) e de elasticidade-renda (1,236). Estes
resultados expressam a importância dessas duas variáveis na determinação do
comportamento do consumo de energia elétrica no Brasil no período 1981/1990,
sobretudo do PIB real. De fato, a partir da análise realizada evidencia que, mantidos
os demais fatores, trata-se de um insumo com demanda inelástica com relação à
tarifa real, mas altamente sensível às variações do nível de atividade da economia.

97. Modelo linear geral e inclusão de variáveis especiais
U2
95
1. Qual é a fórmula para encontrar o valor constante da
regressão múltipla (valor de alfa ou de beta zero)?
2. Qual é a fórmula para o cálculo do coeficiente de
determinação da regressão múltipla?
Nesta unidade você aprendeu sobre:
• O método dos Mínimos Quadrados Ordinários (MQO).
• Pressupostos básicos do MQO.
• A estimação do modelo por meio do MQO.
• Avaliação de modelos estimados.
• Modelo de Regressão múltiplo.
• O processo abreviado de estimativa do modelo geral.
• Deduções matemáticas da média, variância e covariância.
Nesta unidade foi estudado o Método dos Mínimos Quadrados
Ordinários e apresentados os pressupostos do modelo de
regressão linear simples, como também as equações que
permitem estimar os parâmetros. Apresentou-se a avaliação das
estimativas do modelo, exploraram-se as estatísticas de avaliação
e o Modelo de Regressão Múltiplo, com a abordagem das mais

98. Modelo linear geral e inclusão de variáveis especiais
U2
96
variáveis independentes (explicativas) no modelo. Foi estudado acerca
dos critérios para avaliar as estimativas de um modelo, sobre utilizar
um modelo econométrico para tomada de decisão ou previsão.
Você pode complementar seus estudos lendo o Capítulo 4 e 5 do
livro de Econometria, de James H. Stock e Mark W. Watson, publicado
em 2004 e disponível na Biblioteca Digital Pearson. Bons estudos!
1. Observe que: “a regressão consiste em, com base numa
série de dados de duas ou mais variáveis, encontrar uma
equação que represente a relação entre elas. Uma vez
encontrada essa equação, é possível então utilizá-la para
fazer previsões a respeito dos valores de uma das variáveis”.
(VASCONCELLOS, 2000. p. 22). Tomando por base esta
afirmação, apresente um modelo de sua autoria para estudar
algum problema econômico.
2. (ESAF/Auditor Fiscal da Previdência Social/2002) Para
o modelo de regressão linear y = α + βX + ε , onde y é a
variável resposta, X a variável independente, α e β são
parâmetros desconhecidos e ε é uma componente de erro
aleatória com média zero. Assinale a opção que corresponde
à interpretação do parâmetro α.
a) É o valor predito de y, dado que X = 0, desde que esse
valor de X seja compatível com o conjunto de observações
da variável exógena.
b) Mede a variação esperada em y por unidade de variação na
variável exógena.
c) É o valor esperado de y quando se padroniza a variável
exógena.
d) Mede a variação da reta de regressão.
e) Mede o coeficiente angular da reta de regressão.

99. Modelo linear geral e inclusão de variáveis especiais
U2
97
3. Imagine que uma pesquisa sobre venda de um produto
Q, fosse função do preço de venda (P) e do gasto com
publicidade (S). Ao final da pesquisa, após rodar a regressão,
surgiram os seguintes resultados:
^
Q =8,58-0,31 P+0,85 S R2
=0,83.
Observe estes resultados e faça a análise destes para a
empresa.
4. Em relação aos testes que auxiliam na avaliação do
modelo, podemos citar o teste t (Student). Este teste é
importante porque permite identificar o nível de significância
dos parâmetros estimados para cada uma das variáveis
independentes. Neste sentido, apresente os passos
necessários para implementação do teste t.
5. Um importante processo realizado previamente, a análise
de regressão deve ser a análise de correlação entre as
variáveis do modelo. Explique o que é e qual é a diferença
entre a análise de correlação e a análise de regressão.

100. Modelo linear geral e inclusão de variáveis especiais
U2
98

101. Modelo linear geral e inclusão de variáveis especiais
U2
99
Referências
BRANDT, R. D. A procedure for identifying value-enhancing service components
using customer satisfaction survey data. In: SURPRENANT, C. (Ed.). Add value to
your service. Chicago: American Marketing Association, 1987.
BUENO, Rodrigo de Losso da Silveira. Econometria de séries temporais. São
Paulo: Cengagge Learning, 2008.
DORNBUSCH, Rudiger. Macroeconomia. 2. ed. São Paulo: McGraw-Hill, 1991.
ENDERS, W. Applied Econometric Time Series. 2. ed. Wiley, 2005.
GOMES, Fábio A. R. Consumo no Brasil: teoria da renda permanente, formação de
hábito e restrição à liquidez. In: RBE, Rio de Janeiro, 58(3):381-402, jul./set. 2004.
GREENE, William H. Analysis econometric. 5. ed. Upper Saddle River, New Jersey:
Prentice Hall, 2003.
GUJARATI, D. N. Econometria básica. São Paulo: Pearson Makron Books, 2005.
HALL, Robert Ernest. Macroeconomia: teoria, desempenho e política. Rio de
Janeiro: Campus, 1989.
HILL, R. Carter. Econometria. 3. ed. São Paulo: Saraiva, 2010.
______. Econometria. São Paulo: Saraiva, 1999.
LANGE, O. Introdução à econometria. Rio de Janeiro: Fundo de Cultura, 1961.
MATOS, O. C. Econometria básica: teoria e aplicações. São Paulo: Atlas, 2000.
___________. Econometria básica: teoria e aplicações. São Paulo: Atlas, 1995.
MARGARIDO, Marco Antônio. Aplicação de testes de raiz unitária com quebra
estrutural em séries econômicas no Brasil na década de 90. In: Informações
Econômicas, São Paulo, v. 31, n. 4, abr. 2001. Disponível em: <http://www.iea.
sp.gov.br/out/verTexto.php?codTexto=198>. Acesso em: 18 set. 2010.
MANKIW, N. Gregory. Macroeconomia. 5. ed. São Paulo: LTC, 2003.
MORETTIN, Pedro A. Análise de séries temporais. 2. ed. São Paulo: Edgard
Blucher, 2006.

102. U2
100 Modelo linear geral e inclusão de variáveis especiais
U2
100
PINDYCK, R. S.; RUBINFELD, D. L. Econometria: modelos e previsões. Rio de
Janeiro: Elsevier, 2004.
SCHRODER, B; PINA, V. Econometria para concursos. Rio de Janeiro: Elsevier,
2012.
SILVA, Marcos Eugênio. Uma nota sobre esperança condicional e expectativas
racionais. Disponível em: <http://www.econ.fea.usp.br/medsilva/material/eae0308/
textos/Esperanca_Condicional_e_ER1.pdf>. Acesso em: 1º out. 2010.
VASCONCELLOS, Marco A. Manual de econometria: nível intermediário. São
Paulo: Atlas, 2000.
______. Manual de econometria. São Paulo: Atlas, 1995.
WOOLDRIDGE, J. M. Introdução à econometria: uma abordagem moderna. São
Paulo: Cengage Learning, 2011.
______. Introdução à econometria: uma abordagem moderna. São Paulo:
Cengage Learning, 2006.

103. Unidade 3
VIOLAÇÃO DOS PRESSUPOSTOS
BÁSICOS DO MODELO
Nesta seção analisaremos quais são as principais formas de violação
destes pressupostos conhecendo a origem e algumas possíveis formas
de correção.
Seção 1 | Implicações das violações dos pressupostos
básicos do MQO
Objetivos de aprendizagem:Nesta unidade, você terá a oportunidade de
conhecer os principais problemas que surgem da violação dos pressupostos
do Método dos Mínimos Quadrados, bem como compreender as medidas
e solução propostas para superar tais problemas.
Neste sentido, para que você compreenda a dimensão e abordagem destes
problemas, propomos a apresentação desta unidade subdividida em quatro
seções, quais sejam:
Regina Lúcia Sanches Malassise
Nesta seção veremos como a correlação entre duas ou mais variáveis
independentes inclusas no modelo MQO podem interferir nas estimativas
dos parâmetros.
Nesta seção estudaremos como a dependência temporal dos resíduos
torna os resultados do MQO pouco confiáveis.
Seção 2 | Multicolinearidade
Seção 3 | Autocorrelação ou correlação serial

104. Nesta seção verificaremos como a instabilidade da variância do termo
erro pode prejudicar a análise via MQO.
Seção 4 | Heterocedasticidade

105. Violação dos pressupostos básicos do modelo
U3
103
Os pressupostos dos estimadores de mínimos quadrados, que garantem que estes
sejam melhores estimadores lineares não tendenciosos (MELNT), nos informam as
características de um modelo ideal.
Este modelo ideal garante que a reta de regressão apresente aos valores estimados
da variável dependente mais próximo possível o valor real da variável e, portanto,
permite que o modelo possa ser utilizado para previsão.
Ocorre que quando estamos trabalhando com dados econômicos, a possibilidade
de encontrarmos dados para os quais, quando utilizados o MQO estimar os
parâmetros, encontremos estimadores MELNT muitas vezes pequenos.
Nestes casos, ao identificarmos alguma violação dos pressupostos, passamos
imediatamente à fase de busca de soluções para o problema. É evidente que esta
solução passa desde implementação de estratégias estatísticas que permitam
contornar o problema, até mudanças na forma funcional do modelo e pode
chegar à mudança de método de estimação do qual podemos passar para outro
método de estimação.
Introdução à unidade

107. Violação dos pressupostos básicos do modelo
U3
105
Seção 1
Implicações das violações dos pressupostos
básicos do MQO
Recordando os pressupostos básicos do MQO, temos:
Como consequência destes podemos dizer que a utilização do Método dos
Mínimos Quadrados, como ferramenta para estimativa e previsão, somente gera
Esses pressupostos são os seguintes:
I Aleatoriedade de ui
– A variável ui
é real e aleatória ou
randômica.
II Média zero de ui
– A variável ui
tem média zero, isto
é, E(ui
)=0.
III Homoscedasticidade– ui
tem variância constante,
ou seja, var(ui
)=E(ui
2
)= σ2
,ondeσ=constante.
IV A variável ui
tem distribuição normal, isto é, ui
~
N(0,σ^2 ).
V Ausência de autocorrelação ou independência serial
dos u_i. Isso significa que E(ui
uj
)= 0 para i≠j.
VI Independência entre ui
eXi
, ou seja, E(ui
Xi
)=0.
VII Nenhum erro de medida nosX’s – As variáveis
explicativas são medidas sem erros.
VIII O modelo tem especificação correta – Isso
significa ausência de erro de especificação no sentido
de que apenas uma variável explicativa é suficiente
para expressar adequadamente o comportamento do
fenômeno, assim como a forma matemática (linear ou não
linear) é corretamente definida (MATOS, 1995, p. 42-43).

108. Violação dos pressupostos básicos do modelo
U3
106
estatísticas e parâmetros confiáveis a partir da equação estimada, quando atende
a esse conjunto de pressupostos. Por outro lado, a violação de alguns desses é
uma questão de grau e não de natureza, pois sempre ocorrerá de algum modo. O
importante é avaliar-lhe a extensão.
1.1 Principais formas de violação dos pressupostos
Mesmo assim ainda podemos nos perguntar o que aconteceria caso alguns destes
pressupostos fossem violados, quais seriam as implicações para o modelo. De
acordo com Greene (2006), a suposição de que xi
e εi
são não correlacionados é
crucial para utilização do MQO.
Ocorre que algumas vezes estes pressupostos são violados. Porém, existe uma
série de aplicações na economia em que essa suposição é insustentável (GREENE,
2006). Exemplos incluem modelos contendo variáveis que são medidas com erro
e modelos mais dinâmicos, envolvendo expectativas. Sem esta suposição assim o
modelo deixa de ter consistência, então os MQO perdem sua atratividade como
um estimador.
Ao perceber esta dificuldade, o autor complementa dizendo que existe um método
alternativo de estimação chamado método de variáveis instrumentais (VI). Supondo
que, no modelo clássico yi = x’j
β +εi
, os K variáveis xi
podem ser correlacionados
com εi
. Supondo também que exista um conjunto de L variáveis zi
, onde L é ao
menos tão grande quanto K, de tal forma que zi está correlacionada com xi
, mas
não com εi
. Não é possível estimar β consistentemente usando o estimador dos
mínimos quadrados. Mas é possível construir um estimador consistente de β
usando as relações assumidas entre zi
, xi
, e εi
.
E no final o autor reconhece e elenca uma série de dados amostrais que dado suas
particularidades não teriam no MQO um melhor método de estimação para seus
parâmetros, tais como:
A) Painel de dados – examinando um modelo para despesas municipais na forma Sit
= f (Sit-1
,...) + εi
. Os distúrbios são assumidos para serem livremente correlacionados
entre períodos, então ambos Si,t-1
e εi
,t
, são correlacionados com εi
,t-1
. Segue que
eles estão correlacionados uns com os outros, o que significa que este modelo,
mesmo com uma especificação linear, não satisfaz os pressupostos do modelo
clássico. Os regressores e perturbações estão correlacionados.
B) Regressão Dinâmica – examinando uma variedade de modelos de séries de
tempo que sejam da forma yt
= f(yt-1
,...) + εt
em que εt
é autocorrelacionado
com os seus valores passados. Este processo é essencialmente o mesmo que

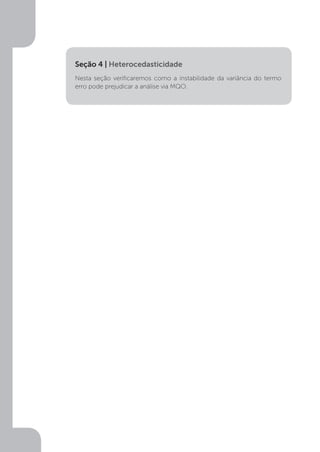
109. Violação dos pressupostos básicos do modelo
U3
107
foi considerado anteriormente. Desde que os distúrbios são autocorrelacionados,
segue-se que a regressão dinâmica implica a correlação entre a perturbação e uma
variável do lado direito. Mais uma vez, os mínimos quadrados serão inconsistentes.
C) Função Consumo – Por construção, o modelo viola os pressupostos do modelo
clássico de regressão. A função renda nacional Y = C + investimento + gastos
governamentais + exportações líquidas. Embora ocorra uma relação exata entre
C de consumo, renda e Y, C = f (Y, ε), é ambíguo e é um candidato apropriado
para a modelagem, é evidente que o consumo (e, portanto, ε) é um dos principais
determinantes da Y. O modelo Ct = α + βYt
+ εt
não se encaixa nas premissas para
o modelo clássico se Cov [Yt, εt] ≠ 0. Mas é razoável assumir (pelo menos por
agora) que εt é não correlacionado com os valores passados de C e Y. Assim, neste
modelo, é possível considerar Yt-1
e CT-1
, como variáveis instrumentais adequadas.
1. Por que não se pode utilizar o método MQO para estimar
parâmetros gerados por painel de dados?
2. Para a função consumo, qual tipo de variável deve ser
criado para resolução de um modelo?

110. Violação dos pressupostos básicos do modelo
U3
108

111. Violação dos pressupostos básicos do modelo
U3
109
Seção 2
Multicolinearidade
Introdução à seção
O problema da multicolinearidade pode ser entendido a partir de um exemplo.
Imagine que você esteja coletando dados para realizar a estimação de um modelo
MQO para a demanda por automóveis em seu município.
Então, em sua pesquisa, você poderia coletar dados tais como: preço do carro,
preço da motocicleta, escolaridade, renda, PIB e PIB per capita, preferência do
consumidor.
Neste caso, poderiam surgir alguns problemas detectados após a estimação do
modelo. Vamos citar alguns: muitos tipos de veículos diferentes, sendo necessário
delimitar melhor qual tipo e modelo de carro; a preferência é subjetiva e difícil
de mensurar e; em economia a renda, renda per capita e PIB estão estritamente
relacionadas, isto é, tem alta correlação.
Neste último caso, dizemos que as variáveis são correlacionadas, ou seja, as
variáveis explicativas medem aproximadamente a mesma coisa. Embora para
Gujarati (2011) sempre exista alguma correlação entre as variáveis explicativas, esta
colinearidade entre as variáveis é uma questão de grau bem como as formas de
correção do problema.
Neste sentido, para compreendermos o problema e verificar as possíveis alternativas
de correção, vamos estudar esta seção.
2.1 Conceito
O entendimento geral sobre a multicolinearidade é que ela surge devido à
existência de relações lineares entre as variáveis independentes do modelo, ou
seja, existe colinearidade. Desta forma, ela pode ser definida como:

112. Violação dos pressupostos básicos do modelo
U3
110
Assim, quando a correlação envolve mais de duas variáveis independentes, o
problema passa a se chamar multicolinearidade. Esta relação pode ser perfeita
(exata) conforme propunha o termo original utilizado por Ragnar Frisch, ou
imperfeita quando as relações são aproximadamente exatas quando podemos
incorporar a existência de um termo de erro estocástico.
Gujarati (2011) argumenta que situações nas quais as variáveis independentes
resultam de formas exponenciais, isto é, uma variável X2
que resulta de uma
variável X1
2
ou uma X3
, por exemplo, que resulte de X2
3
etc. que não descrevem
uma relação linear também serão inclusas num diagnóstico de multicolinearidade.
Assim, o coeficiente de correlação para estas variáveis se apresentará altamente
correlacionado.
Existem diferentes níveis ou graus de multicolinearidade, a Figura 3.1 apresenta um
digrama de representação destas.
COLINEARIDADE. Termo que, em estatística, designa
uma elevada correlação entre duas variáveis, isto é,
ambas têm a mesma trajetória linear. Numa análise de
regressão, duas variáveis independentes podem estar
altamente correlacionadas, mantendo entre si elevada
colinearidade, de tal forma que não é possível estabelecer
o efeito de cada uma delas sobre a variável dependente.
Por exemplo, a elevação das vendas de um produto
(variável dependente) pode ter sido influenciada por um
aumento de salários e pela redução das taxas de juros, não
sendo possível distinguir no curto prazo qual das variáveis
independentes teve a influência maior. Nesse caso, pode-
se utilizar apenas a variável independente julgada a mais
importante (o aumento de salários, no caso), ou combinar
as duas variáveis independentes numa só, ou ainda
escolher uma terceira que substitua as duas primeiras.
Quando existe um grau de correlação muito elevado,
com mais de duas variáveis, o fenômeno é denominado
multicolinearidade (SANDRONI, 1989. p. 108).

113. Violação dos pressupostos básicos do modelo
U3
111
Na figura 3.1, conhecida como diagrama de Ballentini, os círculos Y, X2, X3
representam as variações da variável dependente e as variáveis independentes
respectivamente. O grau de colinearidade é medido pela extensão da área
sombreada, que apresenta a sobreposição dos círculos. Desta forma, o gráfico (a)
apresenta a situação ideal, que seria a ausência de colinearidade entre as variáveis.
O gráfico (b) apresenta colinearidade baixa. O gráfico (c) colinearidade moderada,
(d) elevada colinearidade e (e) colinearidade muito alta.
2.1.1 Principais fontes de multicolinearidade
Segundo Gujarati (2011), é comum de se verificar ou acontecer multicolinearidade
entre as variáveis independentes quando ocorrem alguns fatores específicos tais
como:
Fonte: Gujarati (2011, p. 331)
Figura 3.1 – Visão de multicolinearidade segundo o diagrama de Ballentine
Y
Y
Y Y
Y
X2
(a) No collinearity
(c) Moderate collinearity (d) High collinearity (e) Very high collinearity
(b) Low collinearity
X2
X2
X2
X2
X3
X3
X3
X3
X3

114. Violação dos pressupostos básicos do modelo
U3
112
1) Método de coleta de dados: em alguns casos,
o pesquisador pode ter coletado os dados da amostra
de uma faixa limitada de valores pelos regressores da
população. Em dados econômicos deve-se atentar para
exemplo de situações atípicas para que a coleta considere
esta atipicidade. São exemplos disto a sazonalidade
(comum na agricultura), períodos críticos de política
econômica que criem uma disparidade nos dados como
planos econômicos de combate à inflação, controle de
taxas de câmbio. Mas estas considerações tornam-se
importantes apenas quando as variáveis em estudos estão
relacionadas direta ou indiretamente a estas atipicidades.
2) Restrições ao modelo ou à população que está
sendo alvo da amostra: este problema pode ocorrer
quando as variáveis independentes estão ligadas por uma
lógica econômica intrínseca. Por exemplo, propor um
modelo que vise captar o consumo de energia elétrica
(Y), como uma função da renda (X1) e do tamanho do
imóvel (X2). Pode-se verificar que o tamanho da renda
influencia no tamanho o imóvel, logo rendas maiores
imóveis maiores e vice-versa.
3) Especificação do modelo: a escolha correta da
forma funcional, que não é única, pois cada variável pode
apresentar relações funcionais diferentes em relação
à variável dependente. Por exemplo, caso se incorpore
termos polinomiais em um modelo de regressão quando
a amplitude da variável X for pequena, poderá ocasionar
multicolinearidade. Então estar atendo à combinação de
formas funcionais possíveis é importante.
4) Um modelo sobredeterminado: uma regra
importante a seguir é que um modelo deve ter
número maior de observações do que variáveis
independentes, neste caso o modelo pode incorrer em
alta multicolinearidade, o que impossibilita a estação dos
parâmetros da regressão. Assim refletir sobre as variáveis
essenciais ao modelo e evitar a sobredeterminação
é importante, além disto, num caso como este a regra

115. Violação dos pressupostos básicos do modelo
U3
113
da simplicidade na escolhe de um modelo ficaria
prejudicada devido ao número de variáveis maior que o
de observações.
5) A tendência comum entre variáveis de séries
temporais: em alguns casos as variáveis de série de tempo
caminham na mesma direção, ou seja, tem tendência
comum. Podemos citar como exemplo: consumo e
renda, riqueza e população os regressores (variáveis
independentes) variam na mesma direção e proporção
gerando colinearidade entre elas.
2.1.2 Casos de multicolinearidade
Conforme já argumentado anteriormente, a multicolinearidade é uma questão de grau.
Matos (1995, p. 124-125) argumenta que ela pode ser tratada de acordo com seu grau.
Os três casos identificados pelo autor são:
A – Ausência de Multicolinearidade – ocorre tal caso
quando a correlação entre as variáveis explicativas é
nula, isto é, as variáveis são ortogonais entre si. Essa é a
situação ideal.
B – Multicolinearidade Perfeita – nesse caso, a
correlação entre as variáveis explicativas é igual a 1 ou
a – 1.
O cálculo das estimativas dos parâmetros é,
matematicamente, impossível nessas circunstâncias,
porque o determinante da matriz X`X é nulo.
C – Multicolinearidade Imperfeita – trata-se
da situação em que a correlação entre as variáveis
explicativas situa-se entre 0 e 1 ou entre –1 e 0. É o caso
mais comum.

116. Violação dos pressupostos básicos do modelo
U3
114
2.2 Diagnóstico de multicolinearidade
Em geral, um dos indícios mais claros da existência da multicolinearidade ocorre
quando o R² é alto, mas nenhum dos coeficientes da regressão apresenta valores
estatisticamente significativos para o teste t.
Verifica-se como consequência da multicolinearidade em uma regressão o aumento
da variância da estimativa e, portanto, do erro-padrão.
Tornando a estimativa impossível ou então, no caso de multicolinearidade perfeita, a
impossibilidade de qualquer estimação se a multicolinearidade for perfeita.
A correlação elevada reduz a eficiência, isto representa que um estimador não
tendencioso, mas que apresenta grande variância conduzirá a estimativas distantes
da realidade ou do verdadeiro valor do parâmetro y. Desta forma, verifica-se que o
parâmetro estimado é significativamente afetado, tornando-o instável.
2.2.1 Testes que permitem identificar a presença de multicolinearidade
O problema da multicolinearidade diz respeito à relação existente entre duas ou
mais variáveis independentes. Quanto maior a multicolinearidade, maior a variância
dos estimadores, maiores os erros-padrão e menores os testes t, o que pode levar
a inferências enganosas, como por exemplo, não rejeitar a hipótese nula de que
um determinado coeficiente é igual a zero quando este deveria ser rejeitado.
Pela matriz de correlação podemos verificar, utilizando um exemplo para PIB
e renda, que a correlação simples entre a renda e o tempo é bastante elevada
Em geral, as consequências mais danosas do problema
se verificam à medida que:
a- ocorram não significâncias de variáveis explicativas
com sinais incorretos para algumas delas, ainda que R2
seja elevado;
b- aumente o grau de correlação simples entre as
variáveis explicativas;
c- os parâmetros estimados se tornem instáveis,
quando o tamanho da amostra se altera ou alguma
variável é omitida ou adicionada ao modelo;
d- diminua o determinante da matriz de coeficientes
de correlação entre as variáveis explicativas (MATOS,
1995 p. 126-127).

117. Violação dos pressupostos básicos do modelo
U3
115
(0,94); quando tais correlações superam 0,8, há fortes indícios de existência de alta
colinearidade entre as variáveis.
Outra forma de verificar a colinearidade é através do fator de inflação da variância
(VIF). Diz-se que o VIF médio de um conjunto de regressores não deve ser maior
do que 10 ou que o maior VIF de um regressor não deve ser maior do que 10. Pela
análise da tabela a seguir, vemos que a multicolinearidade é alta nos dados em
questão.
2.2.2 Multicolinearidade e os testes t e F
Quando nos deparamos com esta situação (um ou mais testes t insignificantes
e o teste F significante), provavelmente estamos diante do problema da
multicolinearidade, que se refere à correlação entre duas variáveis explicativas ou
entre uma delas e as demais, incluídas na equação de um modelo. Isso ocorre
quando duas variáveis X1 e X2 medem aproximadamente a mesma coisa. Alguns
aspectos que ressaltam a presença de multicolinearidade são o teste t insignificante
e teste F significativo.
Na presença de multicolinearidade e os componentes das variâncias de MQO
Var (^bj) =
A variância (Var) depende de 3 componentes: σ^2, SQT, R2.
é a variação amostral total em xj.

118. Violação dos pressupostos básicos do modelo
U3
116
A variância do erro, σ2
: um σ2
maior significa variâncias maiores nos estimadores de
MQO: mais ruído na equação (um σ2
maior torna mais difícil estimar o efeito parcial
de qualquer uma das variáveis independentes sobre y, e isso é refletido nas variâncias
maiores dos estimadores de inclinação de MQO.
A variação amostral total em Xj, SQTj: quanto maior a variação total em Xj, menor é
a variância (^bj); assim, tudo o mais sendo igual para estimar ^bj preferimos ter tanta
variação amostral em Xj quanto possível. Já descobrimos isso no caso da regressão
simples.
Embora raramente seja possível escolher os valores amostrais das variáveis
independentes, há uma maneira de aumentar a variação amostral em cada uma das
variáveis independentes: aumentar o tamanho da amostra.
De fato, na amostragem aleatória de uma população, SQTj aumenta sem limite quando
o tamanho da amostra torna-se maior. Esse é o componente da variância que depende
sistematicamente do tamanho da amostra. Quando SQT é pequeno, variância de ^bj
pode ficar muito grande.
O R2
mede o grau de ajuste, um R2
próximo de 1 indica que X2
explica bastante da
variação de X1
na amostra. Isso significa que X1
e X2
são altamente correlacionadas.
Quando R2
cresce em direção a 1, a variância de ^b torna-se maior. Assim, um grau
elevado de relação linear entre X1
e X2
pode levar a variâncias grandes dos estimadores
de inclinação de MQO.
Na presença de multicolinearidade, os estimadores de mínimos quadrados ordinários,
apesar de serem melhor estimador linear não viesado (MELNV) têm grandes variâncias
e covariâncias, o que dificulta uma estimativa precisa. Por esse motivo, a razão t de um
ou mais coeficientes tende a ser estatisticamente insignificante; assim, podemos ter um
t baixo e erro-padrão alto, o que dificulta a estimação de intervalos de confiança, já que
as inferências podem se tornar enganosas, pois há um risco muito grande de se aceitar
a hipótese nula, quando esta deveria ser rejeitada.
2.3 Consequências da multicolinearidade
Podemos citar como principais consequências da multicolinearidade os seguintes
pontos:
1) O estimador de mínimos quadrados não é definido.
2) Quando multicolinearidade é perfeita, não se calcula o determinante e não
se consegue obter os parâmetros.

119. Violação dos pressupostos básicos do modelo
U3
117
3) Quando tal correlação é elevada, a eficiência dos parâmetros estimados
é significativamente afetada, tornando-os instáveis. A consequência é o aumento
da variância da estimativa e, portanto, do erro-padrão. Daí, a estatística t se reduz, e a
hipótese nula H0
pode ser aceita, quando deveria ser rejeitada.
→ Com multicolinearidade torna-se difícil isolar a influência relativa dos Xi
, ficando a
interpretação dos resultados prejudicada.
4)Quandorestápertode1,amulticolinearidadeestápresenteeasvariânciasdos
estimadores se tornam grandes; mesmo que os estimadores sejam não tendenciosos,
será pequena a confiança que podemos ter no valor deles.
5) As variâncias, erros-padrão e covariância dos estimadores de mínimos
quadrados podem ser grandes; grandes erros-padrão implicam alta variabilidade
amostral, instabilidade dos coeficientes estimados em relação a pequenas variações
na amostra ou na especificação do modelo, intervalos de estimação dilatados e
informações relativamente imprecisas proporcionadas pelos dados amostrais sobre os
parâmetros desconhecidos; com erros-padrão altos, não podemos rejeitar H0
.
6) Quando os erros-padrão dos estimadores são grandes, é possível que
os testes t usuais levem à conclusão de que as estimativas dos parâmetros não são
significativamente diferentes de zero, mesmo com altos R2
e F, indicando poder
explanatório significativo do modelo como um todo. O problema é que as variáveis
colineares não proporcionam informação suficiente para estimar seus efeitos separados.
7) A melhor maneira de ver se multicolinearidade está causando problemas é
examinar os erros-padrão dos coeficientes: se vários coeficientes têm erros-padrão altos
e ao retirarmos uma ou mais variáveis da equação se reduz o erro-padrão das variáveis
que permaneceram, a origem do problema normalmente é a multicolinearidade.
Por fim, deve-se investigar se a partir do momento em que se realiza um diagnóstico
de multicolinearidade, qual a gravidade e extensão do problema, pois desta forma é
possível verificar se há propostas para correção do problema que são possíveis de serem
implementadas. De tal forma que possamos utilizar os procedimentos sugeridos por
Matos (1995, p. 129):
Os procedimentos mais comuns visando reduzir suas
consequências são os seguintes:
a. aumento do tamanho da amostra;
b.usodeinformaçãoapriorisobreovalordaestimativa
dos parâmetros, obtida de estudo prévio;

120. Violação dos pressupostos básicos do modelo
U3
118
c. transformação da relação funcional;
d. exclusão das variáveis colineares;
e. uso de razões ou primeiras diferenças.
1. O que se entende por variáveis correlacionadas?
2. Defina colinearidade.

121. Violação dos pressupostos básicos do modelo
U3
119
Seção 3
Autocorrelação ou correlação serial
Introdução à seção
Quando estudamos os tipos de dados verificamos que podemos ter dados do
tipo corte transversal, séries temporais e combinação de corte transversal e série
temporal.
Em estudos de corte transversal, a seleção de amostras é feita de maneira aleatória
e em princípio não há motivos para supor que o termo erro de uma observação
esteja correlacionado com o de outra. Mas existem casos que este problema se
verifica e isto receberá o nome de autocorrelação espacial.
Em estudos que envolvem série de tempo devido ao ordenamento natural das
séries que costuma seguir uma sequência cronológica, levando à observação
de inter-relações entre as observações. Assim, quanto mais curto o espaço de
tempo entre uma observação e outra, maior é a tendência a ter autocorrelação ou
correlação serial. Um exemplo deste tipo de problema ocorre quanto utilizamos
dados de preços de ações.
Desta forma, a autocorrelação é um problema que se verifica nos termos de erro
e que concorre para violação do pressuposto do MQO de que o termo erro é
aleatório e não correlacionado. Para entender melhor este problema vamos
estudar esta seção.
3.1 Conceito
De acordo com Matos (2000), a autocorrelação é um dos problemas mais sérios
em econometria. A autocorrelação ocorre quando há dependência temporal dos
valores dos resíduos, ou seja, quando os resíduos são correlacionados entre si.
Quando há autocorrelação, há violação de uma das suposições do MQO, pois
Cov (εi. εj|X ) ≠ 0, para todo i ≠ j. Na presença de autocorrelação, os termos de erro
(desvios) seguem padrões sistemáticos.
Vale ressaltar que, apesar de os termos autocorrelação e correlação serial serem

122. Violação dos pressupostos básicos do modelo
U3
120
utilizados, muitas vezes, como sinônimos, há certa distinção entre estes dois
termos, conforme explicitado em Gujarati (2011): autocorrelação é a correlação
defasada de uma série consigo mesma, defasada em um número de unidades de
tempo, enquanto o termo correlação serial é utilizado para correlação serial entre
duas séries de tempo. Quando os resíduos são autocorrelacionados, as estimativas
de mínimos quadrados ordinários dos parâmetros não são eficientes (não possuem
variância mínima) e o erro-padrão é viesado, o que leva a testes e intervalos de
confiança incorretos.
As fontes de autocorrelação são: inércia; omissão de variável explicativa (ou erro
de especificação do modelo); má especificação da forma matemática (erro de
especificação do modelo); má especificação do verdadeiro termo aleatório; ajuste
imperfeito de estatísticas. Utiliza-se o teste de Durbin – Watson para verificar a
ausência de autocorrelação. O uso deste teste mostra que o método dos mínimos
quadrados não é adequado, pois apesar de gerar estimadores não viesados, geram
estimadores não consistentes. Daí, deve-se usar o método dos mínimos quadrados
gerais.
3.2 Diagnóstico de autocorrelação: o teste d de Durbin
Este é o teste mais amplamente utilizado para verificar a presença de correlação
serial. Sua formulação é dada pelo quociente entre a soma das diferenças ao
quadrado nos sucessivos resíduos e a soma dos quadrados dos resíduos (SQR):
No numerador da estatística do teste de Durbin-Watson, o número de observações
é n-1, pois se perde uma observação quando se calculam as sucessivas diferenças.
Uma vantagem da estatística d é que ela se baseia nos resíduos estimados, que
são calculados rotineiramente na análise de regressão. Por isso mesmo, muitos
pacotes econométricos informam o d de Durbin-Watson junto a outros resultados
estatísticos, como por exemplo, R2
, R2
ajustado, testes t, entre outros. O uso do
teste d requer algumas observações importantes, conforme alerta Gujarati (2011,
p. 422):
1. O modelo de regressão inclui o termo de intercepto. Se tal termo não estiver
presente, como no caso da regressão que passa pela origem, é importante rodar
novamente a regressão incluindo o termo de intercepto para obter a SQR. 2. As
variáveis explicativas os Xs, são não-estocásticas, ou fixadas em amostras repetidas.
2. As perturbações são geradas pelo esquema autorregressivo de primeira ordem:

123. Violação dos pressupostos básicos do modelo
U3
121
4. O modelo de regressão não inclui valor (es) defasado(s) da variável
dependente como uma das variáveis explicativas. Assim, o teste não é aplicável a
modelos do seguinte tipo:
Em que Yt-1
é o valor de Y defasado de um período. Tais modelos são conhecidos
como modelos autorregressivos. 5. Não há observações que estejam faltando nos
dados.
No teste de Durbin-Watson, não há um valor crítico único que levará à rejeição
ou aceitação da hipótese nula de que não há nenhuma correlação serial entre os
resíduos. Porém tiveram êxitos ao derivar um limite inferior di e um limite superior
ds, de modo que se o d calculado estiver fora desses valores críticos pode-se tomar
uma decisão relativamente à presença de correlação serial positiva ou negativa.
Além disso, estes limites dependem somente do número de observações n e do
número de variáveis explicativas. Estes limites, para n variando de 6 a 200 e para até
20 variáveis explicativas, foram tabulados por Durbin e Watson.
3.2.1 Implementação do teste de Durbin
Um dos pressupostos básicos do MMQ é que o termo erro era aleatório,
independente e com variância constante, ao constatar a existência de correlação
entre os resíduos estaríamos numa situação de autocorrelação serial. Este problema
pode surgir da especificação incorreta do modelo, da omissão de variável relevante
e também procedimentos de dessasonalização da série através de processos de
médias móveis.
Fonte: Pindyck e Rubinfeld (2004, p. 189)
Tabela 3.1 – Teste de Durbin e Watson e interpretações

124. Violação dos pressupostos básicos do modelo
U3
122
A consequência da autocorrelação é que os estimadores dos parâmetros são não
viesados, porém não eficientes (não tem menor variância); além disto as variâncias
estimadas dos parâmetros são subestimados, gerando problemas nos testes de
hipóteses. Para testar a presença de autocorrelação é o Teste de Durbin Watson.
Conceitualmente o teste d é a razão da soma das diferenças, elevada ao quadrado,
entre sucessivos resíduos e a soma dos quadrados do resíduo, dado pela seguinte
fórmula:
O valor de d sempre se situa entre 0 e 4, conforme figura a seguir. A análise será
feita para destacar dois tipos de autocorrelação, a positiva e a negativa, conforme
veremos a seguir sobre a interpretação das estatísticas do teste.
• Para testar a autocorrelação positiva na significância α, a estatística do
teste d é comparado com valores inferiores e superiores crítica (dL, U α
e d, α
):
• Se d <d L, α
, há evidência estatística de que os termos de erro são
positivamente autocorrelacionados.
• Se d> d U, α
, há evidência estatística de que os termos de erro não são
positivamente autocorrelacionados.
• Se d L, α
<d <d U, α
, o teste é inconclusivo.
• Para testar a autocorrelação negativa de significância α, a estatística de
teste (4 - d) é comparada com a inferior e superior os valores críticos (d L, U α
e
d, α
):
• Se (4 - d) <d L, α
, há evidência estatística de que os termos de erro são
negativamente autocorrelacionados.
Fonte: Adaptado de Matos (1995, p. 137)
Figura 3.2 – Gráfico da estatística de Durbin Watson
Área de não rejeição de H0
:
Não existem evidências de autocorrelação
0 dL
du
2 4 - dL
4 - du
4
0 1,04 1,20 2 2,80 2,95 4

125. Violação dos pressupostos básicos do modelo
U3
123
• Se (4 - d)> d U, α
, há evidência estatística de que os termos de erro não são
negativamente autocorrelacionados.
• Se d L, α
<(4 - d) <d U, α
, o teste é inconclusivo.
Considerações importantes sobre as limitações do teste: i) não é apropriado quando
entre as variáveis explicativas esta a variável dependente defasada; ii) no caso de
séries não estacionárias ele só é indicado para os processos AR (1); iii) para utilizar
a estatística o modelo estimado tem que ter o termo constante (VASCONCELLOS,
2000, p. 115).
3.3 Medidas corretivas de autocorrelação
Trataremos de dois métodos, o de Prais-Winsten e o processo interativo de
Cochrane-Orcutt, tomando como referência Gujarati (2011, p. 428).
3.3.1 Quando a estrutura da autocorrelação é conhecida
Supõe-se que ut
= ρut-1
+ εt
com |ρ| < 1 e os εt
seguem as hipóteses de MQO com
média zero, variância constante e ausência de autocorrelação. Se a equação ut
=
ρut-1
+ εt
for válida, a autocorrelação serial pode ser resolvida se o coeficiente de
correlação for conhecido.
Considere as equações:
Yt
= β1
+ β2
Xt
+ ut
(1)
Se (1) for válida para o período t, também será válida para t-1. Portanto,
Yt-1
= β1
+ β2
Xt-1
+ ut-1
(2)
Multiplicando ambos os lados de (2) por ρ temos:
ρYt-1
= ρβ1
+ρβ2
Xt-1
+ρut-1
(3)
Subtraindo (3) de (1), temos
(Yt
- ρYt-1
) = β1
(1 – ρ) + β2
Xt
- ρβ2
Xt-1
+ (ut
- ρut-1
)
= β1
(1 – ρ) + β2
(Xt
- ρXt-1
)+ (εt
) (4)
em que no último passo foi usada a equação ut = ρut-1
+ εt
.
A equação (4) pode ser expressa como:

126. Violação dos pressupostos básicos do modelo
U3
124
Y*t
= β*1
+ β*2
X*t
+ εt
(5)
Em que β*1
= β1
(1 – ρ), Y*t
= (Yt
- ρYt-1
) e X*t
= (Xt
- ρXt-1
)
ComoεtsatisfazassuposiçõesdosMQO,aplicamosMQOàsvariáveistransformadas
Y8 e X* e obtemos estimadores MELNV. Quando rodamos a regressão (5), estamos
rodando uma regressão pelo método dos mínimos quadrados generalizados
(MQG ou GLS). A equação (4) é uma equação de diferença generalizada ou de
quase-diferença, onde regredimos Y sobre X não na forma original, mas na forma
de diferença, subtraindo-se uma proporção (ρ) do valor de uma variável no período
anterior de seu valor no período corrente. Quando fazemos a diferenciação, uma
observação é perdida. Para evitar esse problema, a primeira observação sobre Y
e X é transformada: e X1
→ Esta transformação é chamada
transformação de Prais-Winsten.
3.3.2 Quando a estrutura da autocorrelação é desconhecida
O processo iterativo de Cochrane-Orcutt para estimar ρ. Através deste método
estima-se ρ a partir da estatística d de Durbin-Watson; utilizam-se os resíduos
estimados ut para obter informações sobre o ρ desconhecido.
Considere a equação:
Yt
= β1
+ β2
Xt
+ ut
(6)
Suponha que ut é gerado por um processo AR(1):
ut
= ρut-1
+ εt
(7)
Passos recomendados por Cochrane e Orcutt para estimar ρεt
:
1. Estime o modelo de duas variáveis pelo MQO e obtenha os resíduos, ut
.
2. Use os resíduos estimados para rodar a regressão a seguir:
ut
= ρût-1
+ vt
(8)
que é a contrapartida empírica do esquema AR(1) dado anteriormente.
3. Usando ^ρ obtido de (8), rode a equação de diferença generalizada (4), ou seja,
(Yt
- ρYt-1
) = β1(1 – ^ρ) + β2
(Xt
- ^ρXt-1
)+ (ut
– ^ρut-1
)

127. Violação dos pressupostos básicos do modelo
U3
125
ou
Y*t = β*1
+ β*2
X*t
+ et
(9)
Agora, podemos rodar a regressão já que ρ é conhecido
4. Como, a priori, não se sabe se o ^ρ obtido de (8) é a “ melhor” estimativa de ρ,
substitua os valores de β*1
= β1
(1 – ^ρ) e β*2
obtidos de (9) na regressão original (6)
e obtenha os novos resíduos: ût**, deste modo:
ût
** = Yt
– β*1
- β*2
X*t
(10)
Que pode se calculado facilmente, pois Yt
, Xt
β*1
e β*2
são todos eles conhecidos.
5. Agora estime a regressão:
ut
** = ^^ρû**t-1
+ wt
(11)
que é similar a (3). Assim, ^^ρ é a estimativa de segunda rodada de ρ.
Mas será a estimativa de segunda rodada adequada? Não será a terceira rodada?
O método de Cochrane-Orcutt é repetitivo (iterativo). Mas há uma regra para
sabermos até onde podemos fazer repetições. Deve-se parar de realizar as
repetições quando as sucessivas estimativas de ρ divergirem entre si por uma
pequena quantia, como por exemplo, 0,01 ou 0,005.
Pois bem, agora que compreendemos um pouco dos processos que envolvem a
existência de autocorreção, podemos avançar para o estudo de outro problema
que é a heterocedasticidade.
1. Quando ocorre autocorrelação serial, qual pressuposto do
MQO é violado na presença de autocorrelação serial?
2. Qual é a consequência da autocorrelação para os
estimadores?

128. Violação dos pressupostos básicos do modelo
U3
126

129. Violação dos pressupostos básicos do modelo
U3
127
Seção 4
Heterocedasticidade
Introdução à seção
Quando estimamos um modelo, um pressuposto importante do MQO, é que os
erros ou resíduos sejam homocedásticos quando atendem a este pressuposto.
Todos têm variância mínima e constante, se apresentam concentrados próximos
a uma média.
Ocorre que algumas vezes isto não se verifica, então, pode ocorrer uma forte
dispersão dos dados em torno de uma reta; uma dispersão dos dados perante
um modelo econométrico regredido. Nestes casos temos o que se chama em
econometria de heterocedasticidade.
Por outro lado, podemos dizer que a heterocedasticidade não elimina as
propriedades de inexistência de viés e consistência dos estimadores de MQO, mas
sua principal implicação reside no fato de que os erros apresentando variância
elevada, os parâmetros estimados pela regressão de ter eficiência, ou seja, deixam
de ser os melhores estimadores lineares não viesados. Para compreender melhor
o aspecto vamos estudar esta seção.
4.1 Conceito
Em linhas gerais, a heterocedasticidade pode ser descrita como “conceito de
estatística que designa uma distribuição de frequência em que todas as distribuições
condicionadas têm desvios-padrão (afastamentos) diferentes" (SANDRONI, 1989,
p. 280). Isto é, o erro não é homocedástico.
Apenas relembrando que o pressuposto da homocedasticidade pode ser
representado estatisticamente por [E(ei)2
=σ2+
], significa que cada perturbação
tem a mesma variância σ2
cujo valor é desconhecido. Quando as estimativas
contemplam um termo erro homocedástico, isto garante que cada observação
é igualmente confiável e que as estimativas dos coeficientes da regressão são
eficientes, resultando em testes de hipóteses não viesados.

130. Violação dos pressupostos básicos do modelo
U3
128
Ao contrariar este pressuposto a heterocedasticidade surge de situações para as
quais a variância do termo erro não é constante para todos os valores da variável
independente (Y).Isto é,E(Xi
ei
)≠0; assim [E(ei
)2
≠σ2
]. Desta forma, as principais
consequências da heterocedasticidade é que o MQO não gera estimativas
eficientes ou de variância mínima dos parâmetros, logo os erros-padrões são
viesados e os testes t e F não são confiáveis. A heterocedasticidade é mais comum
em dados de cross-section.
4.2 Identificação da heterocedasticidade
A forma mais simples de constatar a presença da heterocedasticidade é verificar a
plotagem dos termos erros contra cada uma das variáveis explicativas, conforme
podemos ver na Figura 3.3, que compara uma distribuição homocedástica contra
uma heterocedástica.
Esse pressuposto exclui, por exemplo, a possibilidade
de a dispersão das perturbações ser maior para valores
mais altos de Xi. Por exemplo, em uma função de
produção, o pressuposto de Homoscedasticidade implica
que a variação na produção é a mesma, seja a quantidade
de trabalho 20; 100 ou qualquer outro número de
unidades (MATOS, 1995 p. 147).
Fonte: Gujarati (2011, p. 371).
Figura 3.3 – Homecedasticidade versus heterocedasticidade

131. Violação dos pressupostos básicos do modelo
U3
129
Podemos ver também a plotagem do termo erro contra a variável independente,
conforme apresenta a Figura 3.4, num gráfico bidimensional.
Também existem testes estatísticos para detectar a presença ou ausência do
problema da heterocedasticidade. Os mais comuns são os propostos por Goldfeld
e Quandt, Park, Glejser, e Pesaran e Pesaran.
4.2.1 Testes estatísticos para identificação da heterocedasticidade
1) Teste de Goldfeld e Quandt
Os procedimentos para realizar o Teste de Goldfeld e Quandt, de acordo com
Matos (1995), foram apresentados nas linhas a) e d). No decorrer das explicações
presentes nesta unidade, a exemplificação de uma operacionalização utilizando o
Excel contribuirá para uma melhor explicação.
a) Inicialmente, reagrupar os dados, organizando em ordem crescente, o valor da
variável independente Xi
, que, hipoteticamente, encontra-se correlacionada aos
resíduos.
Figura 3.4 – Diagrama de dispersão dos resíduos contra
Fonte: Gujarati (2011, p. 371).

132. Violação dos pressupostos básicos do modelo
U3
130
b) Em seguida, realizar as operações de duas regressões separadas, uma
para os menores valores de Xi
e outra para os maiores valores de Xi
, omitindo
aproximadamente ¼ das observações que tenham valores médios. Portanto, as
(n – c) observações restantes são divididas em duas subamostras de tamanhos
iguais, em uma é necessário incluir os valores menores de X e na outra seus valores
mais elevados.
c) Desta maneira, testa-se a razão entre a soma dos quadrados dos erros da
segunda regressão e a soma dos quadrados dos erros da primeira regressão (isto
é, SQE2
/SQE1
) no intuito de verificar se é significativamente diferente de zero.
d) Partindo dessas informações, é definida a seguinte estatística F:
Com esta fórmula, a estatística tem distribuição F com [(n - c)/ 2 - k - 1] graus de
liberdade tanto para o numerador quanto para o denominador.
Adota-se:
n = número total de observações;
c = número e observações omitidas;
k = número de variáveis explicativas incluídas no modelo.
Constata-se que, se as variâncias das duas subamostras forem iguais, F tender a 1 e
a hipótese nula de ausência de heterocedasticidade (H0
) será aceita.
À medida que a diferença entre as duas variâncias se amplia, o problema de
heterocedasticidade vai se agravando.
Assim, dado um nível de significância, pode-se utilizar a estatística F para verificar a
existência ou não do problema de heterocedasticidade.
Naturalmente, se F observado >F crítico para [(n - c)/ 2 - k - 1] graus de liberdade, a
hipótese nula de homocedasticidade será rejeitada.
Ao trabalhar com grandes amostras, o teste de Goldfeld-Quandt é considerado
o mais indicado, de maneira que seja possível estimar adequadamente as duas
regressões adequadamente.
Em relação à validade, teste de Goldfeld-Quandt requer a normalidade dos resíduos
e a ausência de autocorrelação serial.

133. Violação dos pressupostos básicos do modelo
U3
131
2) Teste de Glejser
Este teste caracteriza-se em estimar a equação de regressão do valor absoluto
dos resíduos ei sobre a variável explicativa, relacionada aos resíduos, depois
da escolha da forma especificativa considera mais adequada. Apesar disto, a
heterocedasticidade se refira à existência de uma relação entre a variância dos
resíduos [var(ei)] e uma ou mais variáveis explicativas (X), a estimação sugerida por
Glejser faz sentido, porque a magnitude de ei em valores absolutos varia (aumenta
ou diminui), quando sua variância não for constante.
Desta forma, temos:
|e|= a + bXc
+ v, onde c = -2; -1; -0,5; 0,5; 1 ou 2
Aheterocedasticidadeé,portanto,avaliadaemfunçãodasestatísticasconvencionais
de análise de regressão (t, F e R2
), rejeitando-se a hipótese nula de ausência de
heterocedasticidade, se os parâmetros estimados forem estatisticamente iguais
a zero, para dado nível de significância. Utiliza-se então a estatística F para a
realização do teste.
Em uma situação quando apenas a estimativa do parâmetro b for diferente de zero,
tem-se heterocedasticidade pura e, desse modo, é plausível admitir que var(ei
) =
σ2
X2c
. Logo, o desvio-padrão será proporcional a Xc
e, em consequência, utiliza-
se Xc como fator de ponderação ou correção da equação original. Se tanto a
estimativa de a quanto a de b forem diferentes de zero, então a heterocedasticidade
será mista e o fator de correção mais apropriado seria o uso da estimativa da (a +
bXc), tornando assim, a correção muito mais complexa e problemática.
Salienta-se, pelo procedimento de Glejser, o fator de correção (Xc
) depende da
forma especificativa que, mais apropriadamente, ajuste |e| a Xc
ou da escolha
arbitrária de uma delas.
3) Teste de Park
Para este teste procede uma especificação que utiliza a relação e2=aXc. Sendo
assim, o teste de homocedasticidade consiste em regredir o quadrado dos
resíduos, e2
, sobre o X, usando-se a forma funcional logarítmica. Assim, desta
maneira, admitindo-se um resíduo aditivo u, a equação a ser estimada apresentada
a seguir será:
Ln e2
=Ln a + cLn X + u
Entretanto, tal forma especificativa não é aplicável no caso de a variável explicativa,
a priori relacionada a e2
, assumir valores negativos ou nulos. Para esta situação,
temos o caso da variável binária.

134. Violação dos pressupostos básicos do modelo
U3
132
Há uma desvantagem, é que o termo u pode, também, ser heterocedástico,
produzindo o erro-padrão viesado e incorreção no próprio teste.
Mesmo assim, a especificação adotada por Park pode ser combinada com o
procedimento sugerido por Glejser, com a vantagem de se poder utilizar o valor
estimado do parâmetro de LnX para a obtenção direta de pesos mais satisfatórios
a fim de corrigir a heterocedasticidade.
A expressão é:
Var (ei
) = σ2
i
= σ2
* Xc
i
.Portanto,
DP (ei) = σi
= (σ2
* Xci)1/2 = σXi
c/2
A estimativa do parâmetro c de LnX possibilita de terminar diretamente os valores
do fator de correção (FC), isto é, FC = Xc/2
. Assim, a equação transformada (sem o
índice i) será correspondente a:
Ao realizar este procedimento, não há necessidade de escolher a melhor forma
especificativa dos valores de c na equação, como é requerido o procedimento
original de Glejser.
4) Teste de Pesaran e Pesaran
O Teste de Pesaran e Pesaran consiste em regredir o quadrado dos resíduos (ui
)
sobre o quadrado dos valores estimados da variável dependente (Y) conforme
veremos na fórmula a seguir:
u2
= a + bY2
+ v
O teste da estimativa do parâmetro b pela estatística t ou F evidencia a significância
ou não da relação acima, e, como resultado, a do grau de heterocedasticidade,
uma característica relevante desse teste é a sua simplicidade.
Assim, também, relaciona os resíduos com os valores estimados da variável
dependente. Isto evita o problema da escolha da variável explicativa que é
correlacionada com os resíduos.

135. Violação dos pressupostos básicos do modelo
U3
133
5) Teste de Normalidade de Jarque-Bera (JB)
Uma das suposições do Modelo Clássico de Regressão Linear é a de que os erros
aleatórios têm media igual a zero. Como o erro é uma variável aleatória e deve ser
estimada no processo de obtenção da reta de regressão, deve-se fazer um teste
que verifique se os erros seguem a suposição de que eles têm seu valor esperado
igual zero.
De acordo com Gujarati (2011), o teste de normalidade JB, é um teste para grandes
amostras (assintótico) e se baseia nos resíduos de mínimos quadrados. A realização
do teste JB requer os cálculos de medidas de assimetria e curtose. A assimetria
se refere ao terceiro momento da distribuição e é definida como: E (X – )3
. A
assimetria é uma medida que fornece o grau de desvio ou afastamento da simetria
de uma distribuição. Quando a curva é simétrica, a média, a moda e a mediana
coincidem num ponto.
A curtose refere ao quarto momento da distribuição e é definido como: E (X –
)4
; é uma medida que reflete o grau de achatamento de uma distribuição. A
assimetria e a curtose são utilizadas para estudar a “aparência” de uma distribuição
de probabilidade.
A medida de assimetria (S) é definida como:
S = (1/N) Σ xi
3
/s3
Onde s é o desvio-padrão de X. Quanto á assimetria, se
S = 0 → Diz-se que a distribuição é simétrica
S < 0 → Diz-se que a distribuição tem assimetria negativa (quando a cauda inferior
tem espessura maior; inclinação à esquerda)
S > 0 → Diz-se que a distribuição tem assimetria positiva (quando a cauda superior
da distribuição é mais espessa do que a cauda inferior; inclinação à direita)
A medida de Curtose (K) é definida como:
Quanto à curtose, temos as seguintes possibilidades:
1. Platicúrtica (K < 3) → Neste caso, a distribuição é achatada (gorda ou de cauda
curta), caracterizando alta variabilidade.
2. Leptocúrtica (K > 3) → A distribuição (fina ou de cauda longa) é concentrada em
torno da média.

136. Violação dos pressupostos básicos do modelo
U3
134
3. Mesocúrtica (K = 3) → A distribuição de frequências é a própria distribuição
normal.
A Figura 3.5 ilustra as possibilidades de curva quanto à curtose. A primeira curva
é Leptocúrtica (mais afilada); a segunda (do meio) é a Mesocúrtica e a terceira (a
mais achatada) é a Platicúrtica.
A estatística do teste de Jarque-Bera, considerando a assimetria e a curtose, é:
Onde A representa assimetria e C representa a curtose e (C – 3) é o excesso
de curtose. Em uma distribuição dita normal, o valor da assimetria é zero e
o valor da curtose é 3. Portanto, o teste é o seguinte: testa-se a hipótese nula
de que os resíduos se distribuem normalmente. Jarque e Bera mostraram que
assintoticamente (isto é, grandes amostras), a estatística JB é distribuído por uma
qui-quadrado com 2 gl. Se o valor p da estatística qui-quadrado calculada em uma
aplicação for suficientemente baixo, podemos rejeitar a hipótese de normalidade
dos resíduos. Mas se o valor de p for razoavelmente alto, não rejeitamos a hipótese
da normalidade.
6) Operacionalização de um teste de Goldfeld-Quandt
Uma das premissas importantes do modelo de regressão linear refere-se à
homocedasticidade, isto é, a variância do termo erro, condicionada aos valores
selecionados das variáveis explicativas, é uma constante, de tal forma que:
Fonte: Disponível em: <http://www.pontodosconcursos.com.br/admin/imagens/
upload/1091_D.doc>. Acesso em: 12 out. 2010.
Figura 3.5 - Exemplos de curva quanto à curtose

137. Violação dos pressupostos básicos do modelo
U3
135
Yi
= α + β+ϵi
E(ui
2
) = σ2
i=1,2,... + n
Porém, pode ocorrer de a variância acompanhar as variações em X e neste caso a
variância de Yi
não será constante, e neste caso a variância será
E=σi
2
A esta violação do pressuposto de homocedasticidade dá-se o nome de
heterocedasticidade. Segundo Gujararati (2006), existem várias razões para que
na prática encontremos dados heterocedásticos. Entre elas podemos citar: os
modelos de aprendizagem pelo erro, a renda discricionária, a existência de dados
discrepantes e a incorreta especificação do modelo, a assimetria de distribuição de
um ou mais regressores incluídos no modelo, a incorreção na transformação dos
dados e a incorreção nas formas funcionais.
A heterocedasticidade seria um problema mais comum em dados de corte que
em séries temporais, pois nas primeiras encontramos uma variabilidade maior
de informações de diferentes ordens e magnitudes coletadas sobre uma mesma
população em um dado ponto do tempo. Verificaremos então como fica a
estimação de βi
m=
n
Σ(xy) - Σx
Σy
n
Σ(x2
) - (Σx
)2
sem heterocedasticidade Var
Na presença de heterocedasticidade a variância de βi
var
Se σi
2
= σ2
para cada i, as duas fórmulas ficam idênticas. Caso contrário βi
continuará sendo não viesado e consistente, porém não terá a menor variância.
“A heteroscedasticidade não elimina as propriedades de inexistência de viés e
consistência dos estimadores de MQO, no entanto, eles deixam de ter variância
mínima e eficiência, ou seja, não são os melhores estimadores lineares não-
viesados (MELNV) devido a incorreções no teste t e F” (MATOS,1995, p. 147).
A forma de correção envolve o método dos mínimos quadrados generalizados
(MMQG), ele é capaz é capaz de considerar a variabilidade maior de informações
desiguais da variável Yi , levando a σi
2
= σ2
a partir da equação de regressão dos
parâmetros estimados por MMQ. Suponha que as variâncias heterocedásticas, σi
2
,
são conhecidas, retomemos equação inicial:

138. Violação dos pressupostos básicos do modelo
U3
136
E dividindo-a por σ1
temos
Agora podemos reescrever a equação em forma de variáveis transformadas:
Sendo E(ui
2
) = σi
2
e este uma constante, logo var (ui
*) = 1. Agora a variância do
termo u_i^* é homocedástico. Agora para mantermos as demais premissas do
MMQ afim de gerarmos estimadores MELNT assumimos que αi
* e βi
* passam a ser
parâmetros estimados no lugar de αi
e βi
.
Podemos detectar a presença de heterocedasticidade através da análise gráfica e
através de testes formais tais como: Teste de Park, Teste de Glejser, Coeficiente de
determinação por ordem de Spearman, Teste de Breusch-Pagan-Godfrey, Teste de
White e Teste de Goldfeld Quandt. Na sequência desenvolveremos um exemplo
numérico, de acordo com dados de Vasconcellos (2000, p.135).
Suponha que tenhamos uma série de dados, conforme descrito na Tabela 3.2. Esta
série poderia ser composta por salários (W) e anos de escolaridade (A).

139. Violação dos pressupostos básicos do modelo
U3
137
Salários. Y1 e Ano X1 = variáveis divididas pelos seus desvios padrões.
Y* e X* = regressão dos valores de Salários Y1 e Anos de estudo X1
Fonte: Adaptado de Gujarati (2011)
Tabela 3.2 – Salários e anos de escolaridade

140. Violação dos pressupostos básicos do modelo
U3
138
Rodamos a regressão na qual W é a variável dependente salários em função dos
anos de escolaridade (A) para a série e encontramos os seguintes valores estimados
pelo Excel expressos no Quadro 3.1:
Desta tabela retiramos os valores da regressão, separando os parâmetros estimados
então, temos:
W = X0
+ β A + ei
W = 124,05 + 177,91 A
(54,91) (4,59)
R2
= 0,98
Apresentamos a Figura 3.6 dos resíduos e a variável explicativa de anos de estudo.
Fonte: A autora (2015).
Quadro 3.1 – Regressão salários em função dos anos de escolaridade com as variáveis originais

141. Violação dos pressupostos básicos do modelo
U3
139
Percebe-se que na medida em que os anos de escolaridade aumentam também
aumentam os resíduos, isto seria indicativo de correlação entre os resíduos e a
variável explicativa A, indicando a presença de heterocedasticidade. Para verificar,
vamos aplicar o teste de Goldfeld-Quandt.
Este teste consiste em encontrar um valor λ (= teste de F). Se σi
2
está relacionado
a Xi então podemos supor que σi
2
= σ 2
Xi
2
, sendo σ_i^2uma constante. Se a
relação descrita for verdadeira, então teremos um caso de heterocedasticidade. A
operacionalização dos testes consiste em ordenar a amostra do maior valor de X
para o menor (conforme coluna 3 da Tabela 1).
Depois dividir a amostra e três partes iguais (conforme marcação mais forte na
Tabela 1), e suprimimos a parte central. Depois realizamos as regressões para a
primeira e para a última parte e encontramos os resíduos SQR1
e SQR2
e montamos
o teste, seguindo a fórmula.
Sendo os graus de liberdade definidos por ((n-c)÷2)-k, sendo n = tamanho da
amostra, c = 3 parte da amostra k = número de parâmetros. Para o nosso exemplo
encontramos os resultados apresentados nos quadros 3.2 e 3.3.
Fonte: A autora (2015).
Quadro 3.1 – Regressão salários em função dos anos de escolaridade com as variáveis originais

142. Violação dos pressupostos básicos do modelo
U3
140
Fonte: A autora (2015).
Quadro 3.2 –Resultados da regressão das 12 primeiras amostras pelos valores originais

143. Violação dos pressupostos básicos do modelo
U3
141
Fonte: A autora (2015).
Quadro 3.3 – Regressão com as amostras sendo padronizadas pelo desvio padrão

144. Violação dos pressupostos básicos do modelo
U3
142
Das regressões do Quadro 3.3 podemos retirar as informações sobre SQR.
SQR1
= 559241,1 e SQR2
= 120315,7
n=27, k = 2 e c=12
λ=4,65
Neste caso, os graus de liberdade do F tabelado será o mesmo no denominador
e no denominador, conforme calculado antes o gl é de 10. Sendo a hipótese nula
H0: ui é homocedástico e Ha
:ui
não é homocedástico. Procuramos o valor na
tabela e comparamos com o valor calculado.
λ = F* = 4,65 e F tab(10,5%)
=2,98.
Neste caso, rejeita-se H0 de que ui é homocedástico, o teste indica que resíduo é
heterocedástico. Neste caso, aplicamos:
Neste caso, os graus de liberdade do F tabelado será o mesmo no denominador
e no denominador, conforme calculado antes o gl é de 10. Sendo a hipótese nula
H0
: ui
é homocedástico e Ha:ui não é homocedástico. Procuramos o valor na
tabela e comparamos com o valor calculado.
λ = F* = 2,11 e F tab(10,5%)
=2,98.
Neste caso, não se rejeita H0e ui é homocedástico. Desta forma, agora os
parâmetros estimados α = 0,1032 e β = 0,99 podem ser considerados MELNT.
Encontramos os novos valores
da regressão.
W = 0,1032 + 0,99 A
(0,046) (0,025)
R2
= 0,97
Refazemos os cálculos para:
SQR1
= 0,024254 e SQR2
= 0,515785
n=27, k = 2 e c=12
λ=2,11
1. O que é heterocedasticidade?
2. Por que podemos ter dados heterocedásticos?

145. Violação dos pressupostos básicos do modelo
U3
143
1. Observe as figuras:
Agora, responda: qual delas traz uma representação de dados
heterocedásticos? Por quê?
Nesta unidade, você pôde compreender, através de análises,
quais são as principais formas de violação destes pressupostos.
Foi apresentada a multicolinearidade, com explicações sobre
uma correlação entre duas ou mais variáveis independentes
inclusas no modelo MQO podem interferir nas estimativas
dos parâmetros. Outro assunto abordado nesta unidade é a
autocorrelação serial e a heterocedasticidade, verificando, assim,
a instabilidade da variância que o termo erro pode prejudicar a
análise via MQO.
Nesta unidade, você aprendeu acerca das implicações das
violações dos pressupostos básicos do MQO. Você pode
complementar seus estudos lendo o Capítulo 7 do livro de
Econometria, de James H. Stock e Mark W. Watson, publicado em
2004 e disponível na Biblioteca Digital Pearson. Bons estudos!

146. Violação dos pressupostos básicos do modelo
U3
144
3. Observe a figura:
4. Observe a figura com a representação do teste de Durbin.
5. Ao identificar um problema de multicolinearidade podemos
atuar seguindo alguns passos para resolução deste problema.
Apresente quais são as formas mais indicadas para corrigir o
problema.
2. Vamos supor que um pesquisador, após rodar um modelo
econométrico, tenha chegado aos seguintes resultados:
C = 0, 331 + 2,033Y – 0,369A R2
= 0,843
Teste t = significante e Teste F = elevado
OBS.: Regressão sujeita a problemas e heterocedasticidade.
Tendo em vista os resultados e a OBS apresentados pelo
pesquisador, o que se pode dizer sobre o modelo?
Considerando que ela represente um
problema de multicolinearidade e
entendendo que esta surge do fato de
as variáveis estarem correlacionadas,
podemos dizer que esta correlação surge
devido a alguns fatores. Nesse sentido,
relacione e explique as principais fontes de
multicolinearidade.
Agora, suponha
que você tenha
recebido o
seguinte valor:
d = 1,25
Classifique os valores apurados para o teste de Durbin (d) em
termos de autocorreção.
Área de não rejeição de H0
:
Não existem evidências de autocorrelação
0 dL
du
2 4 - dL
4 - du
4
0 1,04 1,20 2 2,80 2,95 4

147. Violação dos pressupostos básicos do modelo
U3
145
Referências
BUENO, Rodrigo de Losso da Silviera. Econometria de séries temporais. São
Paulo: Cengagge Learning, 2008.
DORNBUSCH, Rudiger. Macroeconomia. 2. ed. São Paulo: McGraw-Hill, 1991.
ENDERS, W. Applied econometric time series. 2. ed. Wiley, 2005.
GOMES, Fábio A. R. Consumo no Brasil: teoria da renda permanente, formação de
hábito e restrição à liquidez. In: RBE, Rio de Janeiro, 58(3):381-402, jul./set. 2004.
GREENE, William H. Analysis econometric. 5. ed. Upper Saddle River, New Jersey:
Prentice Hall, 2003.
GUJARATI, D. N. Econometria básica. São Paulo: Pearson Makron Books, 2011.
HALL, Robert Ernest. Macroeconomia: teoria, desempenho e política. Rio de
Janeiro: Campus, 1989.
HILL, R. Carter. Econometria. 3. ed. São Paulo: Saraiva, 2010.
______. Econometria. São Paulo: Saraiva, 1999.
LANGE, O. Introdução à econometria. Rio de Janeiro: Fundo de Cultura, 1961.
MATOS, O. C. Econometria básica: teoria e aplicações. São Paulo: Atlas, 2000.
______. Econometria básica: teoria e aplicações. São Paulo: Atlas, 1995.
MARGARIDO, Marco Antônio. Aplicação de testes de raiz unitária com quebra
estrutural em séries econômicas no Brasil na década de 90. In: Informações
econômicas, São Paulo, v. 31, n. 4, abr. 2001. Disponível em: <http://www.iea.
sp.gov.br/out/verTexto.php?codTexto=198>. Acesso em: 18 set. 2010.
MANKIW, N. Gregory. Macroeconomia. 5. ed. São Paulo: LTC, 2003.
MORETTIN, Pedro A. Análise de séries temporais. 2. ed. São Paulo: Edgard
Blucher, 2006.
PINDYCK, R. S.; RUBINFELD, D. L. Econometria: modelos e previsões. Rio de
Janeiro: Elsevier, 2004.

148. U3
146 Violação dos pressupostos básicos do modelo
SCHRODER, B; PINA, V. Econometria para concursos. Rio de Janeiro: Elsevier,
2012.
SILVA, Marcos Eugênio. Uma nota sobre esperança condicional e expectativas
racionais. Disponível em: <http://www.econ.fea.usp.br/medsilva/material/eae0308/
textos/Esperanca_Condicional_e_ER1.pdf>. Acesso em: 1º out. 2010.
VASCONCELLOS, Marco A. Manual de econometria: nível intermediário. São
Paulo: Atlas, 2000.
______. Manual de econometria. São Paulo: Atlas, 1995.
WOOLDRIDGE, J. M. Introdução à econometria: uma abordagem moderna. São
Paulo: Cengage Learning, 2011.
______. Introdução à econometria: uma abordagem moderna. São Paulo:
Cengage Learning, 2006.

149. Unidade 4
FERRAMENTAS E APLICAÇÕES
DA ECONOMETRIA
O estudo analisado objetiva compreender os aspectos básicos de modelo
MQO com inclusão de variáveis especiais (Dummy).
Seção 1 | Consumo de energia elétrica e PIB no Brasil
1970-1996)
Objetivos de aprendizagem: Nesta unidade, você terá a oportunidade de conhecer
mais algumas ferramentas da econometria, bem como aplicações, pois a unidade está
apresentada em forma de composição de artigos.
Nestesentido,estaunidadepretendeapresentarasdiferentestécnicaseconométricas
produzidas pela autora Regina Lúcia Sanches Malassise. Para realizar esta tarefa, a
unidade está composta por três seções:
Regina Lúcia Sanches Malassise
Neste estudo, a partir de dados do Censo Escolar, objetivou-se apresentar
um caminho para a escolha de variáveis e composição de modelos.
Nesta seção, objetivou-se apresentar um tópico mais avançado de
Econometria com a exploração de estudos com dados em painel.
Para melhor compreensão, vamos estudar estas seções.
Seção 2 | Estudo do desempenho da educação
Seção 3 | Estudo sobre a criminalidade

150. Ferramentas e aplicações da econometria
U4
148

151. Ferramentas e aplicações da econometria
U4
149
Introdução à unidade
A econometria constitui-se em um grupo de conhecimentos muito importante para
o economista. Portanto, ler textos e materiais que utilizam técnicas econométricas
e compreendê-los é necessário.
Em termos de leitura, os artigos publicados na área sempre exploram os aspectos
e fundamentos teóricos do problema em questão. Desta forma, a técnica não
pode ser empregada sem construção de uma teoria que fundamente a construção
do modelo. Em termos de linguagem científica, o uso de técnica sem fundamento
teórico bom é o maior motivo para rejeição de publicações e trabalhos em qualquer
área do conhecimento econômico.
Em termos de compreensão, dominar os conceitos e significados dos termos
como intercepto (alfa) e coeficiente angular (beta), compreender os resultados dos
testes estatísticos como teste de t e F e, compreender o significado do coeficiente
de correlação (r) e de determinação (R2) são fundamentais para ler as conclusões
a que o estudo conduziu.

152. Ferramentas e aplicações da econometria
U4
150

153. Ferramentas e aplicações da econometria
U4
151
Seção 1
Consumo de energia elétrica e PIB no Brasil
(1970-1996)
Introdução à seção
Neste trabalho utilizamos o modelo econométrico sugerido por MATTOS (1995, p.
112-123), com a finalidade de estimar uma equação de demanda de energia elétrica
no Brasil para o período de 1970 a 1996. Em seu livro, ele apenas trabalha com o
período de 1970 a 1990, Nossa contribuição foi aumentar o número da amostra
para o período de 1996 e ainda na especificação do modelo não deflacionamos
o PIB, apenas refizemos os cálculos e utilizamos o ano de 1980 para indicativo
índice 100.
1.1 Breve discussão teórica sobre o tema
Analisando os dados do consumo de energia elétrica e do PIB, ambos transformados
em números índices com 1980 = base 100, no período de 1970-1996, temos que
o desenvolvimento das atividades produtivas, da população urbana e dos usos
domésticos é fator que determina a crescente demanda de energia. Alguns dados
apontam que há uma diferença regional no país em termos de consumo de energia,
por exemplo, em 1974, 70% do consumo se concentravam na região Sudeste.
Podemos observar que tanto o consumo de energia quanto o crescimento do PIB
caminham na mesma direção.
Fonte: A autora (2015).
Gráfico 4.1 – Índice de consumo do PIB e energia elétrica no Brasil

154. Ferramentas e aplicações da econometria
U4
152
Como nossa segunda alternativa é verificar o nível de energia no horário de verão
podemos perceber através do gráfico que ocorrem a partir de 1985 algumas
oscilações no consumo de energia elétrica, mas isto ainda não é suficiente para se
afirmar que estas oscilações sejam resultantes do horário de verão e não afetam a
tendência crescente do consumo de energia para os períodos seguintes.
Para obtermos respostas mais apropriadas a esta questão, utilizamos de um modelo
econométrico sugerido por Matos (1995).
1.2 Hipótese
A hipótese formulada para este modelo é de que a quantidade de energia elétrica
demandada na economia é função do crescimento do PIB, da tarifa real média.
Acrescentamos ainda num segundo momento uma variável dummy na tentativa
de captar o efeito do horário de verão nos anos em que o mesmo foi adotado.
O modelo apresentados por Matos (1995) é o que segue:
1.3 Modelo econométrico
1º Momento
As variáveis escolhidas para este trabalho permitem a definição do seguinte modelo:
Y = a + b1
X1
+ b2
X2
+ ui
Onde:
Y = índice de consumo de energia elétrica,
X1
= índice do produto interno bruto,
2º Momento
Y = a + b1
X1
+ b2
X2
+b3
X3
+ ui
Onde:
X3
= dummy para captar efeito do horário de verão nos anos em que ele foi adotado
e, na análise de regressão normal
Y = a + b1
X1
+ b2
X2
+ ui
Y = 7,89 + 1,238 X1 –0,263 X2
R2
= 0,93
(6,81) (-2,92) F = 47,98 n=10
X2
= índice de tarifa real média,
ui
= termo erro da regressão.

155. Ferramentas e aplicações da econometria
U4
153
E na análise de regressão com dummy para captar o efeito do horário de verão:
Y = 5,732 + 1,266 X1
–0,264 X2
- 0,596X3
R2 = 0,93
(2,82) (-2,68) (-0,07) F = 27,34 n=10
1.4 Estimativa do modelo
No modelo proposto temos uma regressão linear múltipla, isto é, admitimos
que o valor da variável dependente (Y) é função linear de duas ou mais variáveis
independentes (X1
e X2
). Os dados aparecem na Tabela 4.1.
Neste caso, após utilizarmos o programa TSP,
chegamos aos seguintes resultados:
Para o Primeiro momento, temos:
Y = α +β1
X1
+ β2
X2
+ ui
Y = 214,70 + 0,41 X1
–1,39 X2
R2
= 0,93
(8,38) (6,60) (-7,03) F = 184,7 n = 27
Análise dos resultados:
Teste t
H0
:β1
= 0 H1
:β1
≠ 0
Como tcalc
= 6,60 > t 24/5%
= 2,064, rejeita-se a
hipótese H0
, e se aceita a hipótese H1
de que β1
é estatisticamente diferente de zero ao nível
de significância de 5%, se o PIB crescer 1% o
consumo de energia cresce 0,41.
H0
:β2
= 0 H1
:β2
< 0
Como tcalc
= -7,03 rejeitam-se a hipótese
H0
, e se aceita a hipótese H1
de que β2
é
estatisticamente diferente de zero ao nível de
significância de 5%, se a tarifa aumentar 1% o
consumo reduz em 1,39 .
Teste F
H0
:β1
= β2
= 0 (ausência de efeito)
Fonte: Adaptado de: Usiskin (1995)
Tabela 4.1 –Índice de produto, tarifa e dummy
para anos de horário de verão

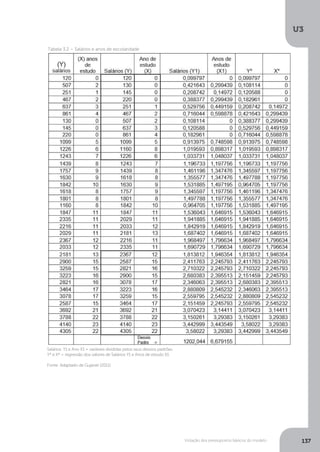
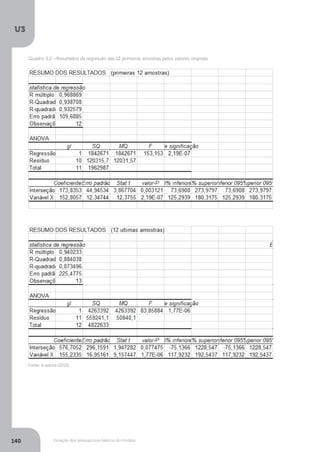
156. Ferramentas e aplicações da econometria
U4
154
H1
:b1
≠ b2
≠ 0 (presença de efeito)
Como Fcalc>Ftab (184,7 > 7,82), rejeita-se a hipótese de efeito nulo das variáveis
explicativas. Isto significa que as variáveis crescimento do PIB e tarifa real média
afetam a quantidade demandada de energia elétrica.
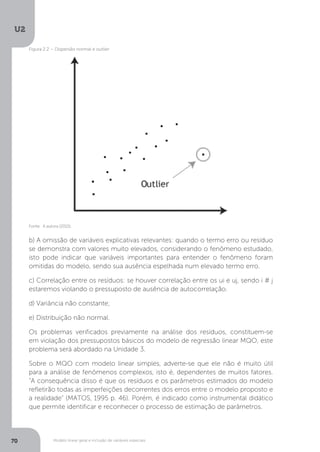
Para o segundo momento, temos:
Y = a + b1
X1
+ b2
X2
+b3
X3
+ ui
Y = 189,73 + 0,31 X1
–1,15 X2
+ 29,56X3
R2
= 0,96
(5,33) (-6,50) (3,50) F = 184,7 n = 27
Com relação aos valores estimados dos parâmetros estimados temos a acrescentar que:
• Todos os parâmetros se mostraram significativos num teste de t, pois o t
23/5% = 2,069 e todos os parâmetros apresentaram valores superiores;
• O coeficiente de determinação (R2
) é significativo;
• O teste de F confirma que as variáveis em seu conjunto exercem
significativa influência no modelo.
Quando comparamos os resultados encontrados com uma amostra maior do que
a do estudo de Matos (1995), com relação à variável dummy, o autor adverte que:
Então observamos que a variável dummy não é significativa numa amostra pequena
nem aumentando o tamanho da amostra, este fato pode ser explicado por dois
motivos, em primeiro lugar porque o crescimento do PIB pode estar aumentando o
consumo rapidamente, outro seria o fato da geração de energia ser menor do que
o necessário para suprir o aumento da demanda.
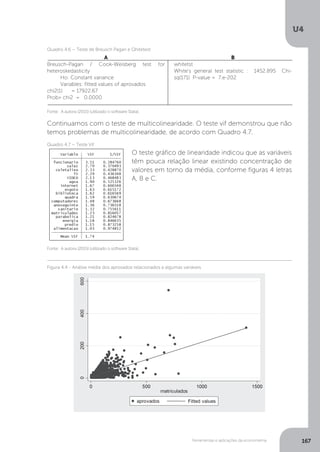
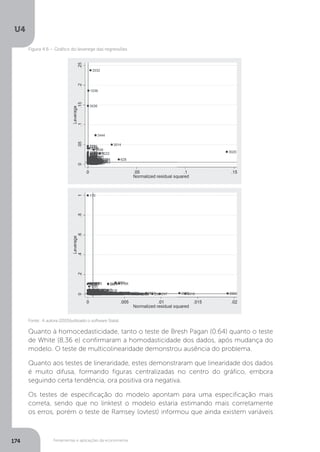
Mas também Mattos adverte para o fato de que podem ocorrer problemas de
multicolinearidade entre as variáveis e entre as variáveis explicativas. Para averiguar
tal situação, procedemos aos testes de multicolinearidade.
Com relação ao efeito individual, registre-se, porém que
a hipótese nula de ausência de efeito é somente rejeitada
no caso das variáveis tarifa real e produto interno bruto, o
que ocorre ao nível de significância de 5%, [...], já o impacto
relativo ao horário de verão, indicado pela dummy, apesar de
negativo como esperado, não se mostrou estatisticamente
significativa, isto implica que a variável não contribui para
explicar o modelo e pode ser excluída, [...], mas as estatísticas
t e F podem alterar-se (MATTOS, 1995, p. 121).

157. Ferramentas e aplicações da econometria
U4
155
Em primeiro lugar, no nosso estudo, o problema da multicolinearidade pode ser
detectado quando não ocorre significância das variáveis explicativas, no caso a dummy,
e quando ocorre alto grau de correlação simples entre as variáveis explicativas.
Procedemos aos cálculos do coeficiente de correlação simples, através do programa
Excel (constatamos que tanto o programa TSP quanto o Excel apresentam resultados
similares com variações pequenas, conforme se pode constatar nos resultados
apresentados nos anexos) e encontramos os seguintes resultados:
r12
= produto e tarifa = -0,7459
r13
= produto e dummy = 0,73
r23
= tarifa e dummy = -0,7854
Após os testes de correlação simples, Farrar e Glauber (1967) propuseram um teste
visando detectar a extensão, localização e padrão de multicolinearidade. Partindo da
elaboração de um novo X2 representado pela seguinte fórmula:
Chegamos aos seguintes resultados:
X2
= (27 – 1 – 1/6 (2.3+5)).Ln (1,8538-1,6982) = X2
= 44,96
Hipóteses H0
: r12
= r13
= r23
= 0 (ausência de multicolinearidade)
H1
: rij
≠ 0 (presença de multicolinearidade)
Como Xcal > Xtab rejetiamos a hipótese nula em favor da hipótese alternativa de
presença do problema.
Procedemos aos testes de localização, regredindo as variáveis explicativas, utilizando
o programa excel, chegamos aos seguintes resultados:
Como os resultados
apresentados pelo teste
de F são significativos,
comprovamos que
existe elevado grau de
multicolinearidade entre
as variáveis explicativas.
Procedemos à exclusão da variável produto conforme indicado por Matos (1995),
e refizemos a regressão no programas TSP e chegamos aos seguintes resultados:

158. Ferramentas e aplicações da econometria
U4
156
1.5 Conclusão
Após a realização de todos estes testes verificamos, diferentemente do que foi
sugerido por Matos (1995), a variável dummy não se mostrou significativa, pois
ela deveria aparecer com sinal negativo indicando, de acordo com a teoria como
redutora do consumo de energia elétrica.
Outro problema pode ser criado quando excluímos a variável produto, podemos
incorrer em erro de especificação do modelo, então concluímos que como a variável
dummy não se mostrou significativa poderia ser excluída do modelo, e poderíamos
então face à presença de outros fatores que afetam o consumo de energia elétrica
propor que o horário de verão poderia não ser eficiente na questão de redução do
consumo de energia elétrica.
Prado (1981), em seu estudo que se deve elevar em conta que a evolução do
consumo de energia elétrica refere-se ao consumo direto e indireto e, no último
caso, o consumo depende da penetração dos diferentes produtos energéticos no
mercado. Com base em dados conclui que:
• A eletricidade terá sua intensidade bastante aumentada, seguindo
tendência histórica de adoção de tecnologias intensivas em capital.
• Graças à sua multiplicidade de usos será cada vez mais usada no âmbito
residencial, especialmente no uso de eletrodomésticos.
• O crescimento devido a mudanças estruturais na economia, referente à
importância dos setores produtivos, também contribui para o aumento do
consumo de energia elétrica.
Então, se quisermos estimar um modelo econométrico para a demanda de energia
elétrica,teremosqueincluirnovasvariáveisaomodelo,quepermitamcaptartalevolução.
1. Qual é o objetivo do estudo apresentado?
2. O que pode ter ocorrido para que a variável dummy não
fosse significativa?

159. Ferramentas e aplicações da econometria
U4
157
Seção 2
Estudo do desempenho da educação
Introdução à seção
Em 2007, comemorou-se 40 anos da intensificação no combate ao analfabetismo
napopulaçãoadultanoBrasil,cujaprimeiraofensivaemmassafoicomoMovimento
Brasileiro de Alfabetização (MOBRAL). Criado pela Lei n° 5.379, de 15 de dezembro
de 1967, propunha a alfabetização funcional de jovens e adultos, visando conduzir
a pessoa humana a adquirir técnicas de leitura, escrita e cálculo como meio de
integrá-la a sua comunidade, permitindo melhores condições de vida. (HISTÓRIA
DA EDUCAÇÃO NO BRASIL, 1993, p. 1). Criado no regime militar, seu objetivo era
alfabetizar adultos que haviam passado da fase escolar. O programa se justificava
porque o Brasil tinha em 1960 o índice de analfabetismo de 39,6% da população
adulta, reduzindo-se para 14,2%, em 1977. Em 2009, segundo dados da PNAD,
esta taxa chega atingiu 9,7%, ou seja, um total de 14,1 milhões de pessoas com 15
anos ou mais de idade (TAXA, 2010, p. 1). E este é um número consideravelmente
expressivo, o que sugere pressões consideráveis sobre a educação de jovens e
adultos no Brasil.
Ainda sobre a regulamentação somente em 1988, a partir do artigo 208 na
Constituição Federal, o direito, mais amplo, à educação básica, seria estendido aos
jovens e adultos como parte de uma estratégia que ampliava os direitos sociais e as
responsabilidades do Estado no atendimento às necessidades dos grupos sociais
mais pobres. Mas, conforme destaca o estudo de Di Pierro (2001), a reforma
educacional de 1990 focalizou a educação básica para a faixa etária de 7 a 14
anos, direcionando os recursos do Fundo de Valorização do Ensino Fundamental
(FUNDEF) para esta faixa modalidade de ensino. Do fundo, foi excluída, a parcela
destinada à educação de jovens e adultos através de um veto do então Presidente
Fernando Henrique Cardoso, alegando que a educação de jovens e adultos oferecia
relação custo-benefício menos favorável quando comparada à educação primária.
Na contramão de tudo isto e devido aos números do analfabetismo, Di Pierro
et al. (2001) argumentam que a clientela dos cursos supletivos se tornava
crescentemente mais jovem e urbana, em função da dinâmica escolar brasileira e
das pressões oriundas do mundo do trabalho.

160. Ferramentas e aplicações da econometria
U4
158
Nesse sentido, mais do que uma "nova escola", voltada
a um novo público, antes não atendido pela escola básica
insuficiente, a educação supletiva converteu-se também em
mecanismo de "aceleração de estudos" para adolescentes
e jovens com baixo desempenho na escola regular [...] a
suplência passou a constituir-se em oportunidade educativa
para um largo segmento da população, com três trajetórias
escolares básicas: para os que iniciam a escolaridade já
na condição de adultos trabalhadores; para adolescentes
e adultos jovens que ingressaram na escola regular e a
abandonaram há algum tempo, frequentemente motivados
pelo ingresso no trabalho ou em razão de movimentos
migratórios e, finalmente, para adolescentes que ingressaram
e cursaram recentemente a escola regular, mas acumularam
aí grandes defasagens entre a idade e a série cursada (DI
PIERRO et al., 2001, p. 5-8).
Di Pierro et al. (2001) advertem que a escassez de recursos para modalidade Ensino
de Jovens e Adultos (EJA) foi contornada pelos municípios de duas maneiras
distintas: ampliação das salas de correção de fluxo e parcerias com organizações
sociais e voluntários, como, por exemplo, o Movimento de Alfabetização (MOVA).
O principal problema advindo destas alternativas resume-se “a descaracterização
da educação de jovens e adultos como modalidade que requer norma própria,
projeto político-pedagógico específico e adequada formação de educadores” (DI
PIERRO, 2001, p. 118).
Outro aspecto importante é que O EJA
tem necessidades especiais a serem
atendidas, pois seu público alvo são
pessoas com 15 anos ou mais e que
na maioria já ingressou no mercado de
trabalho, fato que a nova Lei de Diretrizes
e Bases (LDB) reconhece, pois destaca
que os cursos e os exames devem
proporcionar oportunidades de ensino
apropriadas às condições de vida e
trabalho dos jovens e adultos.
Diante destes aspectos, o presente artigo
visa explorar e descrever um panorama
geral do EJA no Brasil tomando por base
os dados gerados pelo Instituto Nacional
de Estudos e Pesquisas Educacionais Fonte: Shutterstock (2015).

161. Ferramentas e aplicações da econometria
U4
159
Anísio Teixeira, conhecido como INEP, com base nos microdados do Censo
Escolar 2007.
2.1 Metodologia
Todos os anos o INEP realiza o Censo Escolar que é disponibilizado na forma
de microdados agrupados por escola; docentes, turma e matriculados. Estes
dados têm por objetivo fornecer informações estatísticas e servir de subsídio
para a adoção de políticas e estratégias educacionais. Tomando por base os
microdados do Censo Escolar 2007, que trouxe um levantamento no número
de alunos matriculados, bem como o de aprovados na modalidade EJA de 1ª à
4ª série, registrados no agrupamento escola, apresentaremos a seguir algumas
características da infraestrutura das escolas.
A análise apresentada tem por base a utilização de métodos estatísticos quanto
econométricos. A análise estatística aparece inicialmente e tem por objetivos
descrever a infraestrutura existente. Já a análise econométrica, que aparece na
sequência, tem como objetivo identificar as variáveis da infraestrutura física
e administrativa das escolas EJA que interferiram especificamente sobre o
desempenho escolar dos alunos da quarta série do EJA, no ano de 2007. Assim,
a parte econométrica contempla a estimação de uma função que visa estimar o
quanto tais variáveis internas da escola interferem no desempenho/aprovação dos
alunos.
Tendo em vista estes objetivos, o presente artigo está composto de três seções:
descrição das variáveis selecionadas sobre a escola, formulação de hipótese de
trabalho e análise das estimativas e considerações finais.
2.2 Descrição das variáveis selecionadas sobre a escola
Os dados aqui apresentados foram retirados da base de dados utilizando-se diversos
comandos do software Stata. Os comandos utilizados nesta etapa estão no anexo
item 2. Em 2007, o Brasil possuía 81.635 escolas, que ofereciam a modalidade de
ensino EJA. Destas, 78.435 ofereciam EJA Fundamental (primeira à oitava série) e
47.284 ofereciam EJA Médio (primeiro ao terceiro colegial). Estas escolas atendiam
a um total de 4.940.165 alunos distribuídos em ensino presencial (4.330.471) e
semipresencial (608.699). Especificamente sobre as escolas que ofereciam EJA
Fundamental, os alunos matriculados da primeira à quarta série, somavam 473.407

162. Ferramentas e aplicações da econometria
U4
160
sendo que destes 236.794 referiam-se a novos alunos matriculados e 236.613
alunos aprovados, isto é que passaram de ano. Destes alunos aprovados, um total
de 62.715 passou da quarta série, isto é, concluíram o ensino primário. Estes alunos
constituem o público alvo deste trabalho.
Começamos nossa análise trabalhando com a infraestrutura escolar oferecida aos
concluintes da quarta série. Vamos fazer uma descrição da infraestrutura física
(pública, interna e equipamentos) que estas escolas têm, faremos isto porque
nosso objetivo é entender quanto a infraestrutura influencia o desempenho destes
alunos.
As escolas que possuem alunos aprovados na quarta série são 3.676. Destas
escolas, 828 localizam-se na zona rural e 2.848 na zona urbana. Somam um total
de 36.533 salas de aula e contam com 68.376 funcionários. E no ano registraram
um total de aprovados/concluintes da quarta série de 62.715 alunos.
Conforme o Quadro 4.1, observa-se que a maioria das escolas conta com uma
boa estrutura fornecida pelos serviços públicos. Os destaques são para energia
elétrica, coleta de lixo, seguido do fornecimento de água tratada da rede pública,
e em último com um percentual pouco satisfatório aparece o serviço de esgoto,
entendido como vias de escoamento adequado para os resíduos produzidos pela
escola.
Fonte: A autora (2015).
Fonte: A autora (2015).
Quadro 4.1 - Infraestrutura de serviços públicos básicos de que dispõe a escola EJA 1ª à 4ª série
Quadro 4.2 – Infraestrutura interna da escola EJA 1ª à 4ª série

163. Ferramentas e aplicações da econometria
U4
161
O Quadro 4.2 destaca a infraestrutura interna de cada escola, entendida aqui
como itens que aprimoram e melhoram o desempenho escolar por possibilitarem
condições melhores de ensino e promover melhores oportunidades de acesso à
informação, saúde, esporte e lazer. Um dos itens de maior destaque é o prédio
escolar, que segundo Menezes e Santos (2002, p. 112), seria:
As escolas que se classificam como prédios escolares são 96,71%, porém para
atender à conceituação deveriam contar com sanitários e verificamos que apenas
65,5% das escolas contam com sanitários no próprio prédio.
Outro destaque é que maior parte das escolas oferece alimentação, seguida de
biblioteca, acesso à internet e quadra de esportes. Um destaque à parte é a oferta
de quinta série por 46% das escolas, esta variável é considerada importante porque
sinaliza para o aluno concluinte da quarta série que ele pode ir adiante, e como já
está adaptado seria melhor ainda poder continuar na mesma escola.
O Quadro 4.3 destaca a existência de equipamento na escola. A maior parte das
escolas possui televisão e aparelho de vídeo. Porém, os computadores disponíveis
para os alunos são oferecidos por apenas em 38,8% das escolas.
Fonte: A autora (2015).
Quadro 4.3 – Equipamentos e recursos da escola EJA 1ª à 4ª série
1. Edifícios pertencentes a estabelecimentos de ensino
e constituídos de espaços educativos (salas de aula,
laboratórios, salas-ambientes), de serviço (sanitários,
cozinha, cooperativa, serviço médico) e de administração
(direção, secretaria, portaria, arquivo, sala de professores,
almoxarifado) (cf. Centro Regional de Construcciones
Escolares para América Latina, Metodologia para el
Planeamiente de las Construcciones Escolares, México,
1969). 2. Prédios identificados por único endereço, que
serve ao funcionamento de um estabelecimento de ensino.
Os fins de ocupação de um prédio escolar, portanto, são de
desenvolvimento do processo ensino-aprendizagem. Nota:
Rigorosamente, prédio escolar deve ser considerado aquele
construído para fins de ocupação escolar.

164. Ferramentas e aplicações da econometria
U4
162
2.3 Formulação da hipótese de trabalho e análise das estimativas
Antes de começarmos convém fazer uma advertência que sempre começamos
os estudos econométricos pela análise dos dados, esta etapa foi feita inicialmente
e envolveu vários aspectos de correção e seleção de variáveis. Para os dados
observados formulamos a seguinte hipótese de trabalho: o número de aprovados
na 4ª série EJA é uma função do número de matriculados, número de salas de aula,
do número de funcionários, número de computadores disponível para alunos, do
funcionamento em prédio escolar, do fornecimento de água, de energia elétrica,
de esgoto, de coleta de lixo, da existência de quadra de esportes, de biblioteca, de
sanitário no prédio escolar, de equipamentos como TV, vídeo e da existência da
quinta série e do fornecimento de alimentação na escola.
A escolha das variáveis foi feita porque se acredita que seria possível mensurar uma
parte do desempenho escolar (em termos alunos EJA 4ª série aprovados) de teve
a disponibilidade de uma infraestrutura de serviços públicos básicos de que dispõe
as escolas, de uma infraestrutura interna de cada escola e dos equipamentos e
recursos que ela dispõe. Assim, o desempenho escolar pode ser em parte explicado
por variáveis que representam as condições físicas da escola. As estimativas foram
obtidas através do Stata e encontram-se no anexo.
A primeira regressão mostrou que o R2 foi significativo indicando que as variáveis
explicativas contribuem para explicar 42% das variações no número de aprovados.
Sendo que as variáveis significativas, a 10%, e com sinal esperado são matriculados:
sala, computadores, água, TV. E as variáveis significativas com sinal contrário ao
Fonte: A autora (2015) (utilizado o software Stata).
Quadro 4.4 – Regressão inicial

165. Ferramentas e aplicações da econometria
U4
163
esperado foram: funcionário, coleta de lixo. Por outro lado, tivemos 10 variáveis não
significativas. Em primeiro lugar vamos fazer os testes de diagnóstico de regressões
e só depois vamos buscar alternativas que nos permitam corrigir os problemas.
Nossa primeira ação é verificar a correlação parcial entre as variáveis do modelo,
isto porque a não significância das variáveis pode estar associada a problemas de
correlação entre as variáveis e também a heterocedasticidade.
Após rodarmos o correlograma (Tabela 4.5), constatamos que existe correlação
entre as variáveis, porém as correlações mais intensas são entre aprovados e
matriculados (64%), funcionários de salas (77%); água e esgoto (63%). No comando
pwcorr a significância da correlação entre alimentação e funcionário foi (70%),
com biblioteca (85%), quadra (93%) e sanitário (73%). O significado maior disto
é que as escolas que possuem uma infraestrutura completa vão geralmente ter
também alimentação. Isto não quer dizer que uma determina a outra, mas que
onde existe um existe outro.
Identificou-se, também, através da análise visual, numa comparação gráfica dos
erros da regressão versus distribuição normal, que os erros demonstram pequena
variância, porém parecem não seguir uma distribuição normal (Figura 1). Isto se
deve à presença de muitas variáveis binárias no modelo, que conforme testes
confirmaram a não normalidade de sua distribuição e isto contribui para termos
problemas com o resíduo da regressão.
Quadro 4.5 – Correlograma
Fonte: A autora (2015) (utilizado o software Stata).

166. Ferramentas e aplicações da econometria
U4
164
Fonte: A autora (utilização do software Stata)
Figura 4.1 – Distribuição dos erros da regressão versus distribuição normal
Figura 4.2 – Análise dos resíduos da regressão e identificação de outliers
Conforme a Figura 4.2 (A e B), parece haver uma anormalidade maior na distribuição
intermediária dos dados. Conforme a Figura 2 (C e D), confirma-se que a distribuição
dos erros não é bem-comportada, a árvore se mostra mais concentrada na copa. E
pelo da Figura 5 do anexo, percebemos que os maiores problemas de leverage se
encontram nos estados de SP, RJ, CE e PE. Em São Paulo existe grande número de
matriculados, escolas com grande número de salas com número de aprovados três
vezes menor que o número de matriculados, mesmo ocorrendo no Rio de Janeiro. Já
para o Ceará há uma diferença interna nas escolas entre o número de matriculados e
de aprovados para quase todas as escolas, o mesmo se verifica em Pernambuco.

167. Ferramentas e aplicações da econometria
U4
165
Fonte: A autora (2015) (utilizado o software Stata).

168. Ferramentas e aplicações da econometria
U4
166
O segundo procedimento será verificar a homocedasticidade dos resíduos.
Conforme Figura 4.3, do anexo, existe uma concentração de erros, indicando a
heterocedasticidade.
O teste e Bresch Pagan apresentou probabilidade zero, indicando forte presença
de heterocedasticidade, conforme Quadro 1a do anexo. O mesmo ocorrendo
com o teste de White, conforme resultados Quadro 1b.
Fonte: A autora (2015) (utilizado o software Stata).
Figura 4.3 – Análise dos resíduos para cada uma das variáveis do modelo

169. Ferramentas e aplicações da econometria
U4
167
Continuamos com o teste de multicolinearidade. O teste vif demonstrou que não
temos problemas de multicolinearidade, de acordo com Quadro 4.7.
O teste gráfico de linearidade indicou que as variáveis
têm pouca relação linear existindo concentração de
valores em torno da média, conforme figuras 4 letras
A, B e C.
Fonte: A autora (2015) (utilizado o software Stata).
Quadro 4.7 – Teste Vif
Figura 4.4 - Análise média dos aprovados relacionados a algumas variáveis
A
Breusch-Pagan / Cook-Weisberg test for
heteroskedasticity
Ho: Constant variance
Variables: fitted values of aprovados
chi2(1) = 17922.67
Prob> chi2 = 0.0000
B
whitetst
White's general test statistic : 1452.895 Chi-
sq(171) P-value = 7.e-202
Fonte: A autora (2015) (utilizado o software Stata).
Quadro 4.6 – Teste de Breusch Pagan e Qhitetest

170. Ferramentas e aplicações da econometria
U4
168
Fonte: A autora (2015) (utilizado o software Stata).
Quanto à especificação do modelo, o linktest demonstrou aceitação do modelo
que a especificação do modelo está incorreta, pois aponta valor p<0,05. O ovtest
também confirma problemas de especificação do modelo.

171. Ferramentas e aplicações da econometria
U4
169
A
B Ramsey RESET test using powers of the fitted values of aprovados
Ho: model has no omitted variables
F(3, 3654) = 24.74
Prob> F = 0.0000
A
B
C
Quanto aos testes de independência considerando a possibilidade de existência
de autocorrelação das variáveis, foram aplicados os testes Durbin Watson (Quadro
1a), Durbina (quadro 1b), Archlm (quadro 1c) e Breusch Godfrey (quadro 1d). E os
resultados dos testes apontam que não existe autocorrelação entre as variáveis, ou
pelo menos ela não foi significativa o suficiente.
Fonte: A autora (2015) (utilizado o software Stata).
Quadro 4.8 – Linktest (a) e Ovtest
Quadro 4.9 – Testes de independência

172. Ferramentas e aplicações da econometria
U4
170
D
Terminando os testes podemos resumir nossos maiores problemas com o modelo
seria a presença de heterocedasticidade e por isto mesmo a não normalidade dos
resíduos e o mais complicado de todos, a especificação incorreta do modelo.
Podemos adiantar que estes problemas se devem em grande parte à natureza dos
dados com uma diversidade e informações e muitas variáveis binárias, a existência
de outliers severos e a utilização de uma única base de dados que apresenta
dificuldades adicionais devido à descontinuidade da coleta de informações de
maneira sistematizada.
Por exemplo, ao abrir a base 2006 e 2008, constatou-se que não existem a
variável aprovada no 4º ano EJA, impossibilitando levantar em tempo hábil
outras alternativas para o problema. Além disto, muitos dados com informações
inexistentes (.) e outros conflitantes, por exemplo, a escola tem aprovados EJA,
mas não tem matriculados.
Além disto, percebe-se uma distribuição da variável dependente que vai de 1 a
249 com concentração de frequência com 95% dos valores concentrados na
aprovação de 50, e destaque que a aprovação de até 10 é tomar individualmente
5% das observações conforme tabulate. Nosso próximo passo será tentar algumas
alternativas de solução para os problemas encontrados.
2.4 Possibilidades e alternativas de solução para os problemas do modelo
Nosso primeiro passo em direção à busca de melhorias, tanto no indicador de
ajuste do modelo (R2 ajustado) quanto da significância individual das variáveis
independentes do modelo (melhorar o teste t), foi buscar eliminar as observações
com maior leverege, pois de acordo com a análise feita inicialmente nos dados
(comandos describe, codebook e tabulate) havia grandes disparidades entre os
valores das variáveis independentes. Ao aplicar excluir as variáveis leverage, tivemos
uma redução do R2 de 42,6%, conforme item A, para 38,42%, conforme item B do
Quadro 5. Porém, tal redução foi compensada pelo aumento do poder explicativo
individual das variáveis. Se antes tínhamos 7 variáveis significativas, agora passamos
a ter 9 variáveis.
O próximo passo foi buscar a exclusão de variáveis, pois nosso modelo tinha
inicialmente 18 variáveis explicativas, embora este número incluísse mais
observações, na prática um modelo com muitas variáveis e pode implicar uma
solução de problemas mais trabalhosa.
Fonte: A autora (2015) (utilizado o software Stata).

173. Ferramentas e aplicações da econometria
U4
171
Quadro 4.10 – Resumo de testes e regressões rodadas para MQO
O critério utilizado foi excluir variáveis que apresentassem valores insignificantes e
que poderiam ter seu significado expresso em outras variáveis presentes no modelo.
Optamos por excluir a variável energia, embora a correlação com as demais
variáveis fosse baixa, os dados estatísticos apontaram que 98% das escolas têm
energia elétrica e 96% estão em prédio escolar, então de maneira meio intuitiva
podemos afirmar que a maioria das escolas que tem prédio escolar são providas
de energia elétrica e a exclusão da variável não prejudicaria o modelo.
A outra opção foi excluir a variável alimentação, pois apresentava correlação alta
com outras variáveis e a significância destas correlações era considerável. Então,
como 96% das escolas oferecem alimentação e a correlação com biblioteca,
sanitário, quadra e funcionário é alta, acredita-se que mantendo as demais variáveis
e retirando a de alimentação o modelo não seria comprometido.
Ao final destas alterações novamente tivemos uma pequena redução do R2, que
ficou em 38, 15%, conforme item C. Também houve redução no número de
variáveis explicativas significativas agora são 7.
Tentamos nova supressão de variáveis, agora excluindo variáveis de infraestrutura
que poderiam estar presentes na variável prédio. Estas variáveis são energia,
quadra, sanitário. Novamente, conforme verificamos no item D, houve redução
do R2, continuamos com 7 variáveis explicativas significativas, porém com menos
variáveis no modelo (13 variáveis).
Fonte: A autora (2015) (utilizado o software Stata).

174. Ferramentas e aplicações da econometria
U4
172
O próximo passo foi retomar o modelo inicial e refazer uma regressão, mas agora
transformando as variáveis em log, pois, desta forma, estaríamos estimando o
modelo com base nas variações registradas entre as variáveis e não em seus valores
absolutos. As transformações foram aplicadas somente nas variáveis quantitativas,
pois as variáveis binárias e categóricas não apresentam variações significativas.
Agora registramos uma melhora no R2 que ficou em 40,29%, conforme item F, e
temos 8 variáveis explicativas significativas.
Outra alternativa também foi rodar a regressão com as transformações de variáveis
sugeridas pelo comando ladder. Novamente, observando os resultados no item G,
verificamos que houve redução do R2, mas agora temos 9 variáveis explicativas
significativas.
A fim de estimar um modelo com melhor ajuste de modelo e após várias tentativas
de correção melhorias, chegamos à conclusão de que grande número de variáveis
independentes não está contribuindo para um bom ajuste do modelo. Optamos
então por retomar o modelo estimado com variáveis em log e a partir dele excluir
as variáveis que se mostraram insignificantes.
Conforme podemos verificar no item H, o ajuste que retirou as variáveis promoveu
uma melhoria no R2 e principalmente deixou o modelo variáveis com bom poder
explicativo individual, pois todas as variáveis explicativas são estatisticamente
significativas. Tendo alcançado este objetivo vamos refazer o diagnóstico da
regressão agora utilizando este novo modelo.
O teste de normalidade dos resíduos apresentou sensíveis melhoras, conforme
podemos ver a seguir. Houve um espraiamento da variância dos resíduos que
conduzindo a distribuição dos resíduos da regressão para uma distribuição mais
próxima do normal.
Fonte: A autora (utilização do software Stata)
Quadro 4.11 - Regressão final

175. Ferramentas e aplicações da econometria
U4
173
Fonte: A autora (2015)(utilizado o software Stata).
Figura 4.5 – Gráfico de distribuição dos resíduos da regressão versus distribuição normal
Com redução também nos pontos de leverege.

176. Ferramentas e aplicações da econometria
U4
174
Quanto à homocedasticidade, tanto o teste de Bresh Pagan (0.64) quanto o teste
de White (8,36 e) confirmaram a homodasticidade dos dados, após mudança do
modelo. O teste de multicolinearidade demonstrou ausência do problema.
Quanto aos testes de lineraridade, estes demonstraram que linearidade dos dados
é muito difusa, formando figuras centralizadas no centro do gráfico, embora
seguindo certa tendência, ora positiva ora negativa.
Os testes de especificação do modelo apontam para uma especificação mais
correta, sendo que no linktest o modelo estaria estimando mais corretamente
os erros, porém o teste de Ramsey (ovtest) informou que ainda existem variáveis
Fonte: A autora (2015)(utilizado o software Stata).
Figura 4.6 – Gráfico do leverege das regressões

177. Ferramentas e aplicações da econometria
U4
175
omitidas no modelo (0.0414) conforme podemos verificar nas figuras 39 e 40 do
anexo. O resultado do ovtest já era perfeitamente esperado, porque com certeza
outras variáveis importantes como renda, taxa de desemprego, condição na família
influenciam as variáveis do modelo de maneira geral e não somente a variável
dependente. Um resultado melhor para o teste realmente causaria mais espanto
do que entusiasmo.
Todos os testes de independência (Durbin Watson, durbina, archlm e bigdfrey)
demonstraram não haver dependência temporal entre os erros das variáveis.
Foram rodadas, a partir da regressão inicial, inúmeras outras regressões modificadas
para verificar se haveria melhoria da regressão sem desprezar ou omitir variáveis
pré-selecionadas. Como nenhuma dela mostrou melhor, optamos por continuar
com o modelo em log e que excluiu variáveis conforme Quadro 4.5, letra H.
2.5 Considerações finais
Embora a regressão final não tenha um R2 mais elevado que inicial, ela permitiu
encontrar mais variáveis significativas e foi o modelo que melhor se adaptou aos
testes de pressupostos do MQO.
Sabemos que o modelo aqui proposto padece de uma série de dificuldades e
para o mundo real seria necessário incluir mais variáveis que não estão presentes
na base utilizada, cabendo aqui uma ressalva de que o mesmo pode servir para
estudos iniciais com a utilização do Microdados do Censo Escolar.
Sabe-se, também, que esta base apresenta uma série de limitações, entre elas a
mais grave é a descontinuidade das variáveis pesquisadas. Neste estudo poderíamos
futuramente tentar a técnica de regressão com dados em painel, aliás seria mais
adequado para tratar com a diversidade de informações abordadas pelo estudo,
porém a variável dependente de nosso modelo não aparece nos dados das escolas,
nem em 2006 e nem em 2008.
E parece ser uma variável que foi levantada em um ano atípico. Portanto, para
melhor utilização da base as autoridades deveriam privilegiar e montá-las para que
ela fosse um instrumento de pesquisa completo. Quanto ao modelo escolhido e
a explicação para as variáveis, podemos dizer que ao eliminar algumas variáveis,
ainda foi possível captar seus efeitos através das variáveis restantes.
As variáveis de infraestrutura apresentaram o seguinte comportamento: ao manter a
variável prédio escolar, e de acordo com a definição do INEP, no prédio está presente
uma infraestrutura, conforme também observamos na análise estatística. 96 % das
escolas estão em prédio escolar, 98% tem energia, 65% contam com sanitário no
prédio da escola, 56% tem esgoto, 52% têm biblioteca e 45% tem quadra de esportes.

178. Ferramentas e aplicações da econometria
U4
176
Então, para quase 50%, das escolas, o fato de ter prédio pode implicar que elas
tenham também uma infraestrutura, tanto administrativa quanto em termos de
recebimento de serviços públicos básicos, melhor. E que a variável prédio contribui
de maneira positiva com 0,1664 para o desempenho escolar. A variável coleta
de lixo e vídeo está com sinal contrário à teoria. Uma explicação para coleta do
lixo é que ela é frequente na zona urbana e em cidades maiores, gerando aí um
conflito com as cidades pequenas e o número de aprovados nestas que também
é menor, cabe aqui mais estudos. Observação semelhante seria feita para vídeo,
acrescentando o fato de que se trata de um equipamento em desuso.
A variável computador influencia de maneira positiva o que também era esperado,
pois com o avanço das tecnologias, o acesso à informática melhora o desempenho
escolar dos alunos.
Por último, destaca-se o papel do fator humano. Quanto maior o número de
funcionários melhor o desempenho da escola. Outro fator humano é o efeito
ingresso de novos alunos matriculados, variações nela implicam variações positivas
de .69 no número de aprovados.
Isto tem um problema circular porque quanto maior o número de matriculados
maior o número de aprovados para que esta variável não representasse este
problema poderíamos substituí-la por uma Proxy em estudos futuros.
Também acrescentamos o ano seguinte, pois se acredita que em escolas que
oferecem possibilidade de ascensão nos estudos haja um estímulo maior e,
portanto, maior quantidade de alunos aprovados, e realmente variações nesta
provocam variações positivas de 0,09 no desempenho escolar.
Finalmente, argumentamos que o estudo aqui desenvolvido, serve para
encaminhamentos futuros e estudos mais detalhados a respeito do efeito da
infraestrutura escolar sobre o desempenho da escola. Esperamos que o mesmo
suscitasse novos caminhos, projetos e buscas.
1. Qual é a hipótese formulada para o modelo em questão?
2. Depois de realizados todos os testes, quais foram os
problemas apresentados pelo modelo?

179. Ferramentas e aplicações da econometria
U4
177
Seção 3
Estudo sobre a criminalidade
Introdução à seção
Este trabalho objetiva demonstrar como o autor desenvolveu seu estudo
econométrico. No artigo, utilizou o Método dos Mínimos Quadrados Ordinários
e de estimadores com dados em painel para o período de 2001 a 2005. O autor
construiu um painel de dados utilizando diversas fontes de estatísticas, tais como:
Secretaria Nacional de Segurança Pública (SENASP), do DATASUS, IPEADATA etc.
Neste sentido, o trabalho centrará esforços em reproduzir os passos do artigo,
visando explorar e explicar o modelo econométrico utilizado no estudo. Para
cumprir esta meta o presente trabalho está composto de quatro partes. No item
1 faremos uma breve revisão bibliográfica sobre Economia do Crime. No item 2
faremos algumas considerações sobre os modelos com dados em painel. No item
3 rodaremos o modelo estático para efeitos fixos e variáveis. No item 4 tecer-se-ão
as considerações finais.
3.1 Breve explanação sobre a economia do crime
Os primeiros estudos sobre a economia do crime surgiram nos Estados Unidos
no final dos anos 60 com as relevantes contribuições de Becker (1968) e Ehrlich
(1973). Na análise eles propõem uma leitura econômica para as atividades ilícitas,
no sentido de buscar a racionalidade da escolha por parte do agente criminoso.
Ora, sob este ponto de vista, a busca pelas causas da criminalidade por parte de
um indivíduo deve centrar-se nas condições de vida dele, o que não se pode deixar
Um indivíduo cometerá um crime se (e somente se) a
utilidade esperada por este ato exceder a utilidade que
ele teria na alocação de seu tempo e demais recursos em
outras atividades que sejam consideradas lícitas (SANTOS,
2009, p. 170).

180. Ferramentas e aplicações da econometria
U4
178
de investigar são as condições individuais e estruturais sob as quais suas condições
de vida são geradas (SANTOS & KASSOUF, 2008). Assim, uma equação que
busque identificar os determinantes da criminalidade deve conter elementos que
contemplem esta realidade, e isto é feito quando se inclui nela a renda, a educação,
o desemprego e a desigualdade de renda sendo estas variáveis comuns entre a
maioria dos estudos que procuram identificar os determinantes da criminalidade1
.
Por outro lado, para que esta equação ficasse mais robusta, em termos de teoria
microeconômica de tomada de decisão, precisaríamos incluir um item que
considerasse a ideia de ganho de produtividade do crime, ou do ato ilícito. Este
elemento seria próprio das condições individuais, pois dependem da análise que o
indivíduo faz das suas chances de sucesso no ato ilícito2
. Constantemente temos
notícias sobre reincidência do criminoso. Disto se presume que depois que o
indivíduo comete um crime pela primeira vez, ele considera que é mais experiente
na prática ilícita. Além disto, a sensação de impunidade e a convivência em um
meio ilícito também instigam e realimenta a atividade criminosa.
Neste sentido, as condições de vida de um indivíduo em seus aspectos individuais e
estruturais ampliam as diferenças entre a utilidade/retorno que o indivíduo tem do
tempo disponibilizado e dos demais recursos de que dispõe a favor das atividades
ilícitas. Estas duas condições se reforçam o que faz pressupor que um movimento
de inércia faria bastante sentido (KUME, 2004). Por isto vários pesquisadores têm
se dedicado ao estudo da presença de efeito inércia nas taxas de crimes letais nos
estados brasileiros, conforme argumentou Santos (2009) e seu objetivo é apresentar
mais evidências para o efeito inércia sobre a persistência da criminalidade letal no
tempo. Para tanto especificou seu modelo completo nos seguintes termos:
Crimei;t = ηi + ηt + γCrimei,t-1 + β1 Segurança Públicait + β2Educaçãoit +
β3Uniparentalidade Femininait + β4Urbanizaçãoit + β5Desigualdade de Rendait +
β6Juventude Masculinait + β7Rendait + ξit
Em que:
Crimei;t é a taxa de crimes violentos letais e intencionais contra pessoas por cem
mil habitantes no i-ésimo estado (i = 1,..., 26) no ano t (t = 1,..., 5). Dados obtidos da
Secretaria Nacional de Segurança Pública (SENASP);
ηi e ηt são, respectivamente, os efeitos fixos de estado e de tempo;
Crimei,t-1 é a taxa de crimes letais defasada. Variável que representa a dinâmica
do modelo e que, portanto, só aparecerá nas estimativas dos modelos dinâmicos;
1
O autor cita vários artigos, para maiores detalhes consultar a bibliografia de SANTOS (2009)
2
A probabilidade de ele falhar na realização de tal atividade, o que resultaria em prisão, julgamento e punição efetiva se reduzem na
medida em que ele fica mais experiente, pelo menos na visão dele.

181. Ferramentas e aplicações da econometria
U4
179
Segurança Pública (seg) é o total de gastos com segurança pública por cem mil
habitantes, em reais de 2005. Dados do IPEADATA;
Educação (esc) é a escolaridade média, em anos de estudo, dos homens entre 15
e 30 anos de idade, proxy para o custo de oportunidade do crime. Dados da PNAD;
Uniparentalidade Feminina (fam) é o porcentual de famílias uniparentais chefiadas
por mulheres, proxy para o grau de instabilidade familiar e de desorganização
social. Construída a partir dos dados da PNAD considerando famílias chefiadas por
mulheres, sem presença do cônjuge e com filhos de qualquer idade;
Urbanização (urb) é a taxa de urbanização (razão entre a população urbana e a
população total). Utilizados os dados do DATASUS;
Desigualdade de Renda (des) medida pelo coeficiente de Gini e deflacionada pelo
INPC, utilizando dados do IPEADATA.
Juventude Masculina (jov) é a proporção de homens entre 15 e 30 anos de idade
(grupo mais vulnerável ao crime) na população total, controle para o grupo mais
vulnerável ao crime, tanto do lado da oferta quanto da demanda, dados da PNAD;
Renda Familiar (ganhos) é a renda familiar per capita, em reais de 2005, proxy para
os retornos esperados do crime, dados da PNAD e
ξit e o termo erro com as pressuposições usuais.
Adverte-se que nos modelos com efeito fixo e aleatório, por serem modelos
estáticos, não está contemplada a taxa de crime defasada. A variável defasada
será utilizada nos modelos dinâmicos, GMM Diference e System. Sendo que neste
último as variáveis instrumentais serão a taxa e crime defasada e a segurança
pública, ou seja, serão tratadas como potencialmente endógenas, por pressupor
que os investimentos em segurança dependem da criminalidade e que estas
também interferem nos volumes de investimento em segurança.
A expectativa para as variáveis do modelo é que todas apresentem sinais positivos,
isto é, que intensifiquem as taxas de crime. Exceção é feita para β1 e β2 que se espera
tenham sinais negativos, isto é, contribuam para reduzir a taxa de criminalidade.
3.2 Algumas considerações sobre os modelos com dados em painel
O uso dos dados em painel permite estudar dados acompanhando suas variações
ao longo do tempo e também em crosssection, ou seja, trata-se de uma
combinação que recebe a denominação de dados longitudinais (crosssection e

182. Ferramentas e aplicações da econometria
U4
180
séries temporais). O modelo básico utilizado em dados em painel é especificado
da seguinte forma:
Onde Y é a variável dependente; αi
é o intercepto desconhecido para cada indivíduo;
β2
parâmetro da variável independente; X representa o conjunto de variáveis
independentes; β é o coeficiente das variáveis independentes; u é o termo de erro.
Em que os subscritos i é a unidade de corte transversal e, t tempo. Em relação aos
dados pode ser painel balanceado ou desbalanceado. O painel balanceado tem o
mesmo número de observações para cada unidade seccional, onde as unidades
de crosssection (i = 1,..., n) possuem n>1 e períodos (t = 1,... T) T > 1.
Quando o painel é desbalanceado, isso significa que o número de observações
difere entre cada unidade seccional. No presente estudo, o painel é do tipo
desbalanceado porque segundo o autor nos anos de 2004 e 2205, os estados do
Paraná e Pernambuco não publicaram as taxas de crime. Para ser balanceado ele
deveria ter 130 observações (26 estados x 5 anos), como faltaram 4 observações (2
para cada estado) então o painel tem 126 observações.
Outra observação importante é que os estudos com dados em painel contemplam
modelo estáticos e dinâmicos. Segundo MARQUES (2000) num modelo estático
os pressupostos são: as variáveis explicativas são independentes dos termos
erro; a heterocedasticidade está presente nos coeficientes da regressão (porque
variam de indivíduo para indivíduo e no tempo) ou na estrutura do termo erro
(correlacionado com αi ou autocorrelacionado no tempo). Os modelos estáticos
podem ser de sete especificações diferentes e a escolha de um deve considerar
os dados e ao tipo de problema. Aqui os modelos estáticos que nos interessam e
que foram testados no artigo alvo do estudo são os modelos pooled, efeitos fixos
e efeitos aleatórios.
3.3 Painel de dados com modelos estáticos
3.3.1 Modelo de regressão pooled
Neste modelo, combinam-se todos os dados em corte transversal e séries
temporais através do modelo de mínimos quadrados ordinários (MQO). Todas as
observações de cada X são empilhadas e depois estimados os parâmetros por
MQO. Por exemplo, se tivermos observações de 20 anos para um grupo de 4
empresas, o empilhamento produzirá 80 observações para cada variável do
modelo. Assim, a especificação do modelo:

183. Ferramentas e aplicações da econometria
U4
181
Como é estimado por MQO este modelo assume que os erros uit são do tipo
“ruído branco” e não estão correlacionados com os regressores. Este modelo
é chamado de restritivo, pois considera comum para o painel como um todo a
constante e os coeficientes angulares. Este método é apropriado quando se supõe
que os indivíduos possuem características semelhantes Gujarati (2006).
3.3.2 Modelo de efeitos fixos
No modelo de efeitos fixos pode-se levar em conta a individualidade de cada X e
fazer variar o intercepto. Assim, esta técnica pressupõe que as variáveis omitidas
podem levar a mudanças nos interceptos para os dados em corte transversal e
séries temporais. De acordo com Greene (2008), o modelo de efeito fixo implica
que as diferenças entre os grupos podem ser capturadas por diferenças nos termos
constantes. A especificação do modelo seria:
O subscrito i no termo intercepto sugere que o intercepto das 4 empresas pode
ser diferente de uma para outra, porém são invariantes no tempo (os coeficientes
angulares dos regressores não variam entre indivíduos nem ao longo do tempo).
Esta seria uma limitação do modelo que poderia ser contornada utilizando-se
binárias de intercepto diferencial, conforme sugere Gujarati (2006, p. 516). Num
modelo como este os parâmetros estimados, são:

184. Ferramentas e aplicações da econometria
U4
182
A inclusão de dummys para captar diferenças pode se dar no termo i ou para
o termo t ou para ambos. Assim enquanto a constante capta as diferenças que
não variam no tempo as crosssection inclusas no modelo tem função da captar
as diferenças que variam no tempo para o indivíduo em relação a ele mesmo
(dummys para o termo i) e para o indivíduo em relação aos demais indivíduos no
tempo (dummys para o termo t). Para fins do artigo estudado, utilizou-se apenas
o modelo de variáveis binárias de mínimos quadrados (LSDV) e estimaram-se os
interceptos para cada ano.
3.3.3 Modelo com efeitos aleatórios
Segundo Marques (2000), este modelo de componentes de erro introduz a
heterogeneidade individual no termo de perturbação que poderá ser dividido em
duas partes: uma comum, com média nula e variância σ2u
e uma individual, também
com média zero, mas com variância σ2α
e que se assumem independentes. A
especificação do modelo para efeitos aleatórios é a seguinte:
Onde uit
= µit
+ vit
, sendo µi o termo do erro do corte transversal ou específico
dos indivíduos (erro individual), que é constante ao longo do tempo, e vit
o termo
combinado da série temporal e do corte transversal. Em termos de modelos
aleatórios a de se considerar as seguintes restrições impostas sobre os momentos
das variáveis:
4.1 Modelos de painel de dados estáticos: resultados
4.1.1 Regressão Pooled
Comecemos por estimar o modelo MQO, para termos
uma visão sobre o comportamento linear das variáveis
listadas para o estudo. O autor não estimou o modelo
com regressão simples, apenas com dummys. Aqui
optamos por implementar este caminho para verificar
a evolução da qualidade de ajustamento do modelo .

185. Ferramentas e aplicações da econometria
U4
183
Os dados foram empilhados e temos então 126 observações (saída 5). Podemos
observar que temos um teste R e F insignificantes, porém temos 5 variáveis
significativas de acordo com o teste t. As variáveis apresentaram sinal de acordo
com o esperado, a exceção foi a variável segurança. Isto pode acontecer devido a
dois fatos: a heterogeneidade dos dados e a presença de efeitos não observáveis.
4.1.2 Modelo de efeito fixo
Este modelo oferece a possibilidade de captar efeitos de estado não observáveis.
Então se o modelo estimado contiver efeitos de estado não observáveis, as
estimativas dos betas serão tendenciosas e inconsistentes em consequência da
omissão de variável o que pode ser contemplado quando se utiliza um modelo
que explore as características de painel dos dados e permitem o controle pela
heterogeneidade de estado não observável.
No Stata podemos estimar o modelo utilizando o comando xtreg (saída 8) para
estimar modelos de efeitos fixos que estimam a regressão sobre a média de
indivíduos (estados). O efeito é estimado entre estados e o impacto das variáveis
independentes sobre a dependente é estimado para cada grupo (estado) e então
se calcula a média entre os efeitos de tais estados. Este comando também mede
o efeito fixo dentro dos grupos (estados).
Os resultados mostram que o R2 dentro do painel (within) é de 0.15, entre os
painéis (between) é de 0.065 e geral (overall) é de 0.078. Vemos que o R2 é melhor
dentro do painel, porém, ainda baixo, fato que também se destaca no indicador
dos desvios de feitos fixo mais termo erro (sigma_u) de 51,3%. Mas como desvio
padrão somente de ui3
(sigma_e) é proporcionalmente menor (18%) e a variância
de sigma_u, expressa por rho4
, é elevada (88,7%), podemos dizer que o resultado
de R2 era esperado por causa do tamanho da amostra e da omissão de variáveis.
Fonte: A autora (2015) (utilizado o software Stata).
Quadro 4.12 – Estimativa do modelo Pooled
3
Os erros ui referem-se à soma de ai e ei da equação padrão do modelo de efeitos fixos.
4
O termo rho refere-se à variância não explicada pela diferença de uma entidade para outra. Também conhecida como correlação
intraclasse do erro.

186. Ferramentas e aplicações da econometria
U4
184
ortamento linear das variáveis listadas para o estudo. O autor não estimou o modelo
com regressão simples, apenas com dummys. Aqui optamos por implementar este
caminho para verificar a evolução da qualidade de ajustamento do modelo.
O dado relativo à informação corr (u_i, xb) mostra a correlação entre os efeitos
fixos e as variáveis independentes consideradas no modelo. Verifica-se que a
correlação entre os erros ui com os regressores no modelo de efeitos fixos é
–0,5045, considerada muito alta, indicando a presença de efeitos específicos não
observáveis. O teste F para verificar se ui=0 com média zero, rejeita a hipótese de
que o erro seja randômico e bem distribuído em torno da média, confirmando a
conclusão anterior. Assim, os efeitos fixos são bastante importantes no modelo,
sendo e as características whitin estão determinando as diferenças.
4.1.3 Efeito aleatório ou randômico
Este modelo admite que a distribuição dos efeitos fixos ou que a diferença entre
os indivíduos/entidades tem uma distribuição bem-comportada com média zero.
Considera-se, portanto, não haver correlação entre estes efeitos e as variáveis
independentes do modelo, conforme se observa na corr (u_i, X) = 0 (assumed)
da saída 15, ele também é conhecido como modelo de correção de erros. No
Fonte: A autora (2015)(utilizado o software Stata).
Quadro 4.13 – Regressão painel com efeito fixo

187. Ferramentas e aplicações da econometria
U4
185
entanto, este modelo considera que as observações de cada indivíduo (estado)
têm um elemento comum, o ui, o que produz autocorrelação dos erros dentro
do próprio indivíduo (estado), o que produz estimadores de MQO não eficientes
e os erros padrão inválidos. Portanto, deve-se utilizar a estimação de mínimos
quadrados generalizados (MQG) (GUJARATI, 2006, p. 526).
4.1.4 Entre o efeito fixo e aleatório
A escolha sobre qual deles utilizar pode ser feita através da aplicação de um teste
formal chamado teste de Hausman. O teste cria uma variável com distribuição χ2
assintótica e consiste em avaliar se os coeficientes estimados usando o modelo de
efeitos fixos ou aleatórios são idênticos. A hipótese nula do teste de Hausman é a
de que as diferenças nos coeficientes não são sistemáticas, isto é, os estimadores
do modelo de efeitos fixos e do modelo de efeitos aleatórios não apresentam
diferenças substanciais. Se houver rejeição da hipótese nula, isto significa que o
mais indicado é o modelo de efeitos fixos.
Conforme demonstra a saída 17, as diferenças entre os coeficientes são sistemáticas,
indicando que o melhor modelo seria o estimado para efeitos não observáveis
aleatórios.
Fonte: A autora (2015)(utilizado o software Stata).
Quadro 4.14 – Regressão dados em painel efeito aleatório

188. Ferramentas e aplicações da econometria
U4
186
Porém, vários pesquisadores afirmam que a escolha de qual dele é o melhor deve-se
pautar também pela teoria econômica a priori, pois nas palavras de Dias (2010, p. 5)
E conforme argumento Santos (2009, p. 177) em nota:
Eu particularmente gosto da sugestão do Hsiao (1992).
Os efeitos ai e ui representam a ignorância do investigador
e, portanto, compreendê-la o máximo possível deve ser
nosso objetivo. Ainda segundo o autor os modelos diferem
no seguinte:
I) o modelo de efeito fixo serve para avaliar o resultado
condicional aos efeitos existentes na amostra. Portanto, o
resultado vale somente para a amostra.
II) o modelo de efeito randômico faz análise incondicional,
sendo os resultados válidos para a população.
No caso da criminalidade é muito mais plausível utilizar
o modelo de Efeitos Fixos do que o modelo de Efeitos
Aleatórios, pelo fato de que os efeitos específicos de estado
não observáveis, potencialmente, são correlacionados com
as variáveis exógenas do modelo. Assumir esta hipótese é
bastante razoável no caso da criminalidade, pois é plausível
que a qualidade das instituições de segurança pública e
privada esteja associada ao nível de renda do estado, ou,
então, que os conflitos pessoais estejam de alguma forma
ligados ao nível de desigualdade de renda e assim por diante.
Fonte: A autora (2015)(utilizado o software Stata).
Figura 4.15 – Quadro comparativo

189. Ferramentas e aplicações da econometria
U4
187
5.1 Considerações finais
A realização deste trabalho cumpriu com seu objetivo de conseguir percorrer os
caminhos já trilhados por um pesquisador, através da reprodução de seu trabalho
e de seus resultados. Podemos argumentar que outros aspectos positivos e
produtivos podem ser destacados, conforme segue:
1. Ao empreender a busca por um material que permitisse a reprodução com a
utilização das técnicas de Econometria, podemos tomar contato com colegas
pesquisadoresdeoutrasinstituiçõeseestabelecerumcanaldetrocadeinformações
muito importante para o crescimento e desenvolvimento de pesquisa.
2. Através do trabalho, tomar conhecimento de outra área dos estudos de
economia, a Economia do Crime, tomando contato com uma extensa bibliografia,
nacional e internacional na abordagem sobre o tema.
3. Podemos aprofundar os conhecimentos de estudos de dados em painel, com
a utilização de método dinâmico e que contemple a possibilidade de desenvolver
estudos nos quais a combinação de equações em níveis e em diferenças nos
permita captar, a existência de efeitos específicos não observáveis, com o uso de
painel de dados estáticos.
4. E por último, intensificar a troca de experiências entre os colegas de curso. Este
maior entrosamento permite que possamos trabalhar em grupo que amplia as
nossas possibilidades em termos de produção científica.
5. Podemos dizer que foi uma experiência enriquecedora no sentido de que
promoveu profunda conscientização da necessidade de estar sempre em busca
de aperfeiçoar e ampliar os conhecimentos existentes.
1. Qual é a racionalidade da escolha em cometer um crime
segundo a indicação da teoria utilizada no estudo?
2. Qual é a vantagem do uso de painel de dados para estudos
econométricos?

190. Ferramentas e aplicações da econometria
U4
188
Nesta Unidade, exploramos algumas aplicações da
econometria. Você pode complementar seus estudos
lendo o Capítulo 8, 9 e 10 do livro de Econometria, de
James H. Stock e Mark W. Watson, publicado em 2004 e
disponível na Biblioteca Digital Pearson. Bons estudos!
Nesta unidade destacamos a implementação de um MQO
com inclusão de dummy, Vimos como podemos proceder
à escolha de variáveis de um modelo por meio da análise de
dados. E, por fim, verificamos os passos para compreender
os modelos com dados em painel.
1. A Econometria utiliza-se de métodos quantitativos
para estimar relações entre variáveis dependentes
e independentes. Por outro lado, a avalidade destas
estimativas depende dos resultados apresentados pelos
testes que permitem validar ou não as conclusões que o
modelo econométrico pode expressar. Neste sentido,
destaque as principais conclusões dos testes e dos
resultados gerais do modelo apresentado na Seção 1.
2. O jornal Valor Econômico publicou a seguinte manchete
“Consumo de energia no Brasil cai 0,9% em março”.
(Disponível em: <http://www.valor.com.br/brasil/4025292/
consumo-de-energia-no-brasil-cai-09-em-marco>.
Acesso em: 28 abr. 2015). Segundo o jornal, o cenário
econômico de baixa produção e o clima mais ameno

191. Ferramentas e aplicações da econometria
U4
189
ajudaram na queda do consumo. Considerando o estudo
apresentado na Seção 1, que pararelo você poderia fazer
entre a manchete e o que foi apresentado na Seção 1?
3. Num estudo sobre infraestrutura nas escolas brasileras
intitulado "Uma escala para medir a infraestrutura escolar",
realizada pelos pesquisadores Joaquim José Soares Neto,
Girlene Ribeiro de Jesus e Camila Akemi Karino, da UnB
(Universidade de Brasília), e Dalton Francisco de Andrade, da
UFSC (Universidade Federal de Santa Catarina) e comentada
pelo UOL Educação. (Disponível em: <http://educacao.uol.
com.br/noticias/2013/06/04/menos-de-1-das-escolas-
brasileiras-tem-infraestrutura-ideal.htm>. Acesso em: 25
maio 2015). Os pesquisadores informaram que a criança,
quandochegaàescola,temqueterequipamentos,conforto
do ambiente para se concentrar, se dedicar aos estudos e
ao aprendizado. O professor precisa de equipamento para
desenvolver o trabalho dele, assim como a escola, explica
Joaquim José Soares Neto. "O Brasil está passando por
um momento em que é consenso que se deve investir
em educação. A pesquisa traz uma perspectiva de como
orientar esse investimento para resolver um problema que
não é simples" (p. 1). Neste sentido, em nosso estudo da
Seção 2, apresentamos a correlação entre as variáveis do
modelo proposto na seção. Apresente a correlação destas
variáveis.
4. Ainda tomando como base o enunciado da questão
3, complemente sua análise apresentando os principais
resultados do modelo proposto na seção.
5. O pesquisador que pretende utilizar modelagem
econométrica em seus estudos deve se prevenir em relação
aos obstáculos presentes na busca de dados, definição
de variáveis, formatação de modelos e dentre estes itens
também desenvolver um bom relacionamento com demais
pesquisadores do tema. Neste sentido, na Seção 3, foram
apresentados resultados de um estudo anterior no qual se
propuseram pequenas alteraçãos, nas conclusões finais
destacaram-se algumas partes do processo de pesquisa.
Descreva quais são estes itens.

192. Ferramentas e aplicações da econometria
U4
190

193. Ferramentas e aplicações da econometria
U4
191
Referências
ANUÁRIO ESTATÍSTICO DO IBGE (1991-1997). Instituto Brasileiro de Geografia e
Estatatística. Rio de Janeiro: AEB, 1998.
BLUNDELL, R.; BOND, S. Initial conditions and moment restrictions in dynamic
panel data models. Journal of Econometrics, 87:115-143, 1998.
CAMERON, A. C.; TRIVEDI, P. K. Microeconometrics using Stata. Texas: Stata
Press, 2010.
CONJUNTURA ECONÔMICA. IBRE: Rio de Janeiro, 1998.
DI PIERRO, M.C; JOIA, O: RIBEIRO, V. M. Visões da educação de jovens e
adultos no Brasil. Cad. CEDES, Campinas, v. 21, n. 55, nov. 2001. Disponível em:
<http://www.scielo.br/scielo.php?pid=S0101-32622001000300005&script=sci_
arttext&tlng=es>. Acesso em: 20 nov. 2010.
DI PIERRO, Maria Clara. Notas sobre a redefinição da identidade e das políticas
públicas de educação de jovens e adultos no Brasil. Rev: Educ. Soc., Campinas, v.
26, n. 92, p. 1115-1139, Especial – Out. 2005. Disponível em: <http://www.scielo.br/
scielo.php?pid=S0101-32622001000300005&script=sci_arttext&tlng=es>. Acesso
em: 20 nov. 2010.
DIAS, J. Análise de dados em painéis. Notas de aula. UEM/PCE, Maringá, 18 nov.
2010.
FARRAR, D. E.; GLAUBER, R. R. Multicollinearity in regression analysis: The Problem
Revisited. The review of economics and statistics. 1967.
GREENE, W. H. Econometric analysis. 6. ed. New Jersey: Prentice Hall, 2008.
GUJARATI, D. N. Econometria básica. São Paulo: Pearson Makron Books, 2006.
HISTÓRIA DE EDUCAÇÃO NO BRASIL. Vitória, 1993. Disponível em: <http://www.
pedagogiaemfoco.pro.br/heb10a.htm>. Acesso em: 28 nov. 2010.
MENEZES, Ebenezer Takuno de; SANTOS, Thais Helena dos. INEP (Instituto
Nacional de Estudos e Pesquisas Educacionais - verbete). Dicionário Interativo
da Educação Brasileira. São Paulo: Midiamix, 2002. Disponível em:< http://www.
educabrasil.com.br/eb/dic/dicionario.asp?id=373>. Acesso em: 8 mai. 2015.

194. U4
192 Ferramentas e aplicações da econometria
KUME, Leonardo. Uma estimativa dos determinantes da taxa de criminalidade
brasileira: uma aplicação em painel dinâmico. In: Anais do XXXII Encontro
Nacional de Economia, João Pessoa. ANPEC. 2004. Disponível em: <http://www.
ppge.ufrgs.br/giacomo/arquivos/direito-penal/kume-2004.pdf>. Acesso: 25 maio
2015.
MARQUES, Luis D. Modelos dinâmicos com dados em painel: revisão de
literatura. Out. 2000. Disponível em: <http://www.fep.up.pt/investigacao/
workingpapers/wp100.pdf>. Acesso em: 25 maio 2015.
MATTOS, Orlnado Carneiro de. Econometria básica: teoria e aplicações. São
Paulo: Atlas, 1995.
PINDYCK, R. S.; RUBINFELD, D. L. Econometria: modelos e previsões. Rio de
Janeiro: Elsevier, 2004.
PRADO, Luiz T. S. A utilização do modelo de MDEE na avaliação da demanda de
energia no Brasil. Estudos Econômicos, São Paulo, USP, n. especial 7-22, p. 161-18,
set. 1981.
REYNA, O. T. Panel data analysis: fixed & random effects. Disponível em: <http://
dss.princeton.edu/training/Panel101.pdf>. Acesso em: 15 nov. 2010.
ROODMAN, D. An introduction to diference and system GMM in stata. Working
Paper 103, Center for Global Development, 2006.
SANTOS, Marcelo Justus. Dinâmica temporal da criminalidade: mais evidências
sobre o efeito inércia nas taxas de crimes letais nos estados brasileiros. Revista
Economia, jan./abr. 2009. Disponível em: <http://www.anpec.org.br/revista/vol10/
vol10n1p169_194.pdf>. Acesso em: 25 abr. 2015.
SANTOS, M. J.; KASSOUF, A. L. Estudos econômicos das causas da criminalidade
no Brasil: evidências e controvérsias. Revista Economia, maio/ago. 2008.
Disponível em: <http://www.anpec.org.br/revista/vol9/vol9n2p343_372.pdf>.
Acesso em: 25 abr. 2015.
TAXA de analfabetismo cai 1,8% em cinco anos no Brasil, mostra Pnad. G1.
08/09/2010. Disponível em: <http://g1.globo.com/vestibular-e-educacao/
noticia/2010/09/taxa-de-analfabetismo-cai-18-em-cinco-anos-no-brasil-mostra-
pnad.html>. Acesso em: 28 nov. 2010.
WOOLDRIDGE, J. M. Introdução à econometria: uma abordagem moderna. São
Paulo: Cengage Learning, 2006.