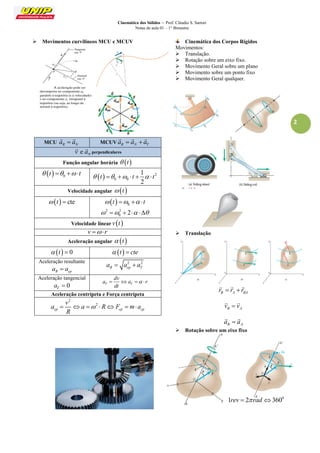
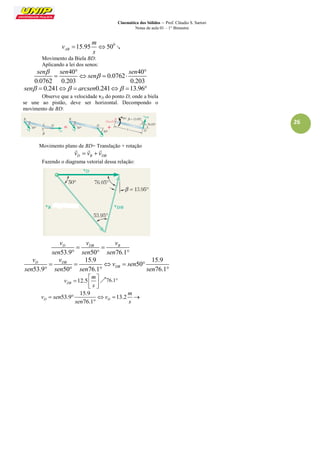
1. O documento apresenta as notas de aula sobre cinemática dos sólidos, abordando conceitos como vetor posição, velocidade e aceleração para partículas e sólidos. 2. São apresentados os objetivos gerais e específicos da disciplina, conteúdo programático, bibliografia e exemplos resolvidos sobre rotação com eixo fixo. 3. O resumo explica que durante rotação com eixo fixo, todos os pontos do sólido apresentam trajetórias circulares com a mesma vel

1. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
1
EMENTA
Desenvolvimento e aplicação das equações vetoriais que relacionam
as várias grandezas cinemáticas envolvidas no estudo dos
movimentos de sólidos. Classificação dos movimentos do sólido.
Aplicação dos princípios e equações cinemáticas nos movimentos de
dispositivos compostos por vários sólidos e vínculos.
OBJETIVOS GERAIS
 Desenvolver no aluno uma visão factível da mecânica,
criando no mesmo uma "intuição" correta dos fenômenos mecânicos.
 Capacitar o estudante de engenharia a entender e resolver
problemas que envolvam a cinemática dos sólidos e dispositivos, que
são comuns no exercício da profissão de engenheiro.
OBJETIVOS ESPECÍFICOS
 Estabelecer os conceitos básicos sobre Cinemática do
Sólido. Preparar os alunos para entender os dispositivos mecânicos
comuns à vida do Engenheiro.
 Fornecer ferramentas aos estudantes para entender e
acompanhar em bom nível as disciplinas específicas do curso, em
especial aquelas ligadas à cinemática de dispositivos, vibrações e
outras.
 CONTEÚDO PROGRAMÁTICO
1. Cinemática da Partícula;
(a) Vetor Posição;
(b) Vetor Velocidade;
(c) Vetor Aceleração;
i. aceleração tangencial;
ii. aceleração normal;
2. Cinemática do Sólido;
(a) Classificação dos Movimentos;
(b) Movimento de Translação;
i. equações vetoriais de velocidade e
aceleração;
(c) Movimento Plano;
(d) Rotação com Eixo Fixo;
i. equações vetoriais de velocidade e
aceleração;
(e) Movimento Plano em geral;
i. equações vetoriais de velocidade e
aceleração;
(f) Centro Instantâneo de Rotação;
(g) Movimento Geral;
 BIBLIOGRAFIA Básica
BEER, F. P.; JOHNSTON JUNIOR, E. R. Mecânica vetorial
para engenheiros: cinemática e dinâmica 5ª ed. 2v. São
Paulo: Makron, 1994.
HIBBELER, R. C. Dinâmica: Mecânica para Engenharia.
8.ed. Rio de Janeiro Prentice Hall Brasil, 2004.
KRAIGE,L.G.;MERIAN,J.L. Mecânica: dinâmica. Rio de
Janeiro: LTC,2004.
FRANÇA, L.N.F.;MATSUMURA,A.Z. Mecânica Geral.Edgar
Blucher, 2005.
GERE, J. Mecânica dos materiais. São Paulo: Pioneira Thomson
Learning, 2003
KAMINSKI, P.C. Mecânica geral para engenheiros. Edgar
Blucher, 2000.
SEARS,F.;YOUNG H. D. Física. vol.1, Mecânica. Addison Wesley,
2008.
Cinemática dos Sólidos,Unip, Versão 2, 2009.
 Vetor Posição: r  x iˆ  y  ˆj  z kˆ

 Vetor velocidade média m v

:
m
r
v
t





 Vetor Velocidade instantânea:
dr
v
dt



 Vetor aceleração média: m
v
a
t





 Vetor Aceleração instantânea:
dv
a
dt



 Aplicação: Lançamento Oblíquo:
 Eixo x: MU: 0 0x
x  x  v  t
 Eixo y: MUV:
2
0 0 2 y
t
y  y  v  t  g 
0y y v  v  g  t
 Decomposição da velocidade inicial 0 v

:
0 0 0 0 cos
x y
v  v   v  v  sen
 Tempo de subida:
0y
s
v
t
g

 Alcance:  
2
0 2 m
v
x sen
g
 
 Altura máxima:
0
2
2
y
v
h
g


2. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
2
 Movimentos curvilíneos MCU e MCUV
MCU R N a  a
 
MCUV R N T a  a  a
  
e N v a
 
perpendiculares
Função angular horária  t 
  0  t    t   2
0 0
1
2
 t    t    t
Velocidade angular  t 
 t   cte   0  t    t
2 2
0    2 
Velocidade linear v t 
v   r
Aceleração angular  t 
 t   0  t   cte
Aceleração resultante
R cp a  a
2 2
R cp T a  a  a
Aceleração tangencial
0 T a 
T T
dv
a a r
dt
   
Aceleração centrípeta e Força centrípeta
2
2
cp cp cp
v
a a R F m a
R
      
Cinemática dos Corpos Rígidos
Movimentos:
 Translação.
 Rotação sobre um eixo fixo.
 Movimento Geral sobre um plano
 Movimento sobre um ponto fixo
 Movimento Geral qualquer.
 Translação
B A BA r  r  r
  
B A v  v
 
B A a  a
 
 Rotação sobre um eixo fixo
0 1rev  2 rad 360

3. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
3
dr
v
dt



ds
v s BP BP r sen
dt
       
d
v r sen
dt

    v  r   sen
Velocidade angular:    kˆ
 
Como o ângulo entre r

e  
é , lembrando da
propriedade do módulo do produto vetorial:
 r  r   sen  r   sen  v
  
v  r
  
 
dv d d dr
a a r r
dt dt dt dt

        
  
     
d
a r v
dt

   

   
Aceleração angular:
d
dt

 


  kˆ  kˆ   kˆ
    
a  r   r 
     
 Rotação de uma placa em torno de um eixo fixo:
Sendo   kˆ
 ˆ v  r v  k r
    
Como kˆ  r v  r 

a  r   r 
     
a   kˆr   kˆ  kˆr 
  
  a   kˆr 2  kˆ kˆr
  
kˆkˆr 

u v w  u wv u v w
        
kˆkˆr   kˆ  r kˆ kˆ kˆr
  
kˆkˆr   r
 
a  kˆr 2  r
  
 Aceleração tangencial:
ˆ
T T a  k r a   r
 
 Aceleração normal
2 2
N N a    r a   r
 
Resumo: Rotação com eixo fixo:
1. Todos os pontos apresentam trajetórias circulares.
2. Todos os pontos apresentam a mesma velocidade
angular, e esta tem a direção do eixo de rotação:
ˆ ˆ
d
e e
dt

     
 
A direção do vetor velocidade angular é ortogonal ao
plano formadopelo movimento do ponto P, possui a direção
do eixo de rotação do sólido.
O sentido do vetor velocidade angular é dado pela regra
da mão direita: o ponto P, deslocando-se no sentido anti-horário,
acompanha-se o sentido do movimento de P ao longo
de sua trajetória circular, com os quatro dedos da mão direita;
com exceção do polegar que indicará seu sentido, apontando
para o ponto A.
3. Todos os pontos apresentam a mesma aceleração
angular, e esta tem a direção do eixo de rotação:
ˆ ˆ
d
e e
dt

     
 
4. O vetor velocidade instantânea no ponto P é dado por:
P
P P
dr
v v r r P A
dt
      

    
5. O vetor aceleração do ponto P é dado por:
dv
a v a
dt
   

     P P a  r    r
     
a  P A  P A
   
 Exemplos Resolvidos
1. Ache os vetores velocidade e a aceleração dos pontos
1.1 Os discos indicados para cada caso, em cada instante
de tempo. O disco parte do repouso em t = 0s.
(a) α = 2 rad/s2; =4rad/s, t = 3 s; Pontos A e B.
B

4. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
4
(b) α = 2 rad/s2; t = 3 s; ; Pontos A e B, C e D.
 Ponto B:
0.2 cos30 ˆ 0.2 30 ˆ B r    i   sen  j

0.173 ˆ 0.1 ˆ B r   i   j

2
2 ˆ
rad
k
s

 
   
 

0 0 2 3 6
rad
t
s
         
6 ˆ
rad
k
s

 
   
 

6 ˆ 0.173 ˆ 0.1 ˆ B B B v  r v   k   i   j
   
     
ˆ ˆ
6 0.173 ˆ ˆ 6 0.1 ˆ ˆ B
j i
v k i k j

       

0.6 ˆ 1.038 ˆ B
m
v i j
s
 
      
 

B BT BN a  a  a 
  
B B B a  r  v
    
BT B a  r
  
2 ˆ 0.173 ˆ 0.1 ˆ
BT a   k   i   j

     
ˆ ˆ
2 0.173 ˆ ˆ 2 0.1 ˆ ˆ
BT
j i
a k i k j

       

2
0.2 ˆ 0.346 ˆ
BT
m
a i j
s
 
      
 

BN B a  v
  
6 ˆ  0.6 ˆ 1.038 ˆ
BN a   k    i   j

      
ˆ ˆ
6 0.6 ˆ ˆ 6 1.038 ˆ ˆ
BT
j i
a k i k j

        

2
0.828 ˆ 3.6 ˆ
BN
m
a i j
s
 
      
 

0.2 ˆ 0.346 ˆ 0.828 ˆ 3.6 ˆ
BT BN
B
a a
a    i   j    i   j
 

 
2
1.028 ˆ 3.254 ˆ B
m
a i j
s
 
      
 

1.2 O sistema ilustrado, composto por placas soldadas a
um eixo fixo AB, gira em torno deste, com velocidade angular
 = 5 rad/s, que cresce a taxa de 4 rad/s2. No instante
ilustrado, o ponto E está descendo. Pedem-se:
(a) o vetor velocidade angular.
(b) o vetor aceleração angular.
(c) a velocidade do ponto D.
Pontos x y z (x,y,z)
A 0 0.203 0 (0,0.203,0)
B 0 0 0.152 (0,0,0.152)
D 0.178 0 0 (0.178,0,0)
BA  A BBA  0,0.203,00,0,0.152
 
BA  0,0.203,0.152

BA  0 iˆ  0.203 ˆj 0.152kˆ

 2 2 2 BA  0  0.203  0.152  BA  0.254
 
0 ˆ 0.203 ˆ 0.152 ˆ ˆ ˆ
0.254 0.254 0.254
BA
e e i j k
BA
    


eˆ  0 iˆ  0.8 ˆj 0.599 kˆ
  eˆ  5 0 iˆ  0.8 ˆj 0.599 kˆ
 
  0 iˆ  4 ˆj  2.977 kˆrad s

  eˆ  4 0 iˆ  0.8 ˆj 0.599 kˆ
 
  0 iˆ 3.202 ˆj  2.397 kˆ rad s2   

  0 iˆ  4 ˆj  2.977 kˆrad s

AD  D A AD  0.178,0,00,0.203,0
 
AD  0.178,0.203,0

AD  0.178 iˆ 0.203 ˆj 0 kˆ

v   AD
  
v  0 iˆ  4 ˆj  2.977 kˆ0.178 iˆ 0.203 ˆj  0 kˆ

ˆ ˆ ˆ ˆ ˆ
0 4 2.977 0 4
0.178 0.203 0 0.178 0.203
i j k i j
v 
 

0.608 ˆ 0.533 ˆ 0.712 ˆ
m
v i j k
s
 
        
 

z
x
y
B
A C
0.203 m
0.152 m
0.178 m
D
E
30°
B
C
D
45°
60°

5. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
5
  D a   D A  v
   
 
ˆ ˆ ˆ ˆ ˆ
0 3.202 2.397 0 3.202
0.178 0.203 0 0.178 0.203
i j k i j
  D A  
 

 D A  0.487 iˆ 0.427 ˆj 0570 kˆ

 
D
DA
v
D
r
  D A  v
 
     
 
 


    

ˆ ˆ ˆ ˆ ˆ
0 4.002 2.997 0 4.002
0.608 0.533 0.712 0.608 0.533
i j k i j
 v  
    
 
 v  4.447 iˆ 1.822 ˆj  2.433 kˆ
 
  D a   D A  v
   
0.487 ˆ 0.427 ˆ 0 570 ˆ
4.447 ˆ 1.822 ˆ 2.433 ˆ
a i j k
i j k
        
     

2
4.934 ˆ 1.395 ˆ 3.003 ˆ
m
a i j k
s
 
        
 

2. No problema anterior, determine a velocidade e a
aceleração no vértice D, supor que a velocidade angular é  =
5 rad/s e aumenta à razão de 20 rad/s2.
  0 iˆ  4 ˆj  2.977 kˆrad s

  eˆ  20 0 iˆ  0.8 ˆj 0.599 kˆ
 
  0 iˆ 16 ˆj 11.98 kˆ rad s2   

v  0 iˆ  4 ˆj  2.977 kˆ0.178 iˆ 0.203 ˆj  0 kˆ

ˆ ˆ ˆ ˆ ˆ
0 4 2.977 0 4
0.178 0.203 0 0.178 0.203
i j k i j
v 
 

0.608 ˆ 0.533 ˆ 0.712 ˆ
m
v i j k
s
 
        
 

AD  0.178 iˆ 0.203 ˆj 0 kˆ

v   AD
  
v  0 iˆ  4 ˆj  2.977 kˆ0.178 iˆ 0.203 ˆj  0 kˆ

ˆ ˆ ˆ ˆ ˆ
0 4 2.977 0 4
0.178 0.203 0 0.178 0.203
i j k i j
v 
 

0.608 ˆ 0.533 ˆ 0 712 ˆ
m
v i j k
s
 
         
 

  D D a   D A  v
   
 
ˆ ˆ ˆ ˆ ˆ
0 16 11.98 0 16
0.178 0.203 0 0.178 0.203
i j k i j
  D A  
 

 D A  2.4319 iˆ  2.13244 ˆj  2.848 kˆ

   D     D A  v
   
ˆ ˆ ˆ ˆ ˆ
0 4.002 2.997 0 4.002
0.608 0.533 0.712 0.608 0.533
i j k i j
 v  
    
 
 v  4.447 iˆ 1.822 ˆj  2.433 kˆ
 
  D a   D A  v
   
2.4319 ˆ 2.13244 ˆ 2.848 ˆ
4.447 ˆ 1.822 ˆ 2.433 ˆ
a i j k
i j k
       
     

2
6.8789 ˆ 0.31044 ˆ 0.415 ˆ
m
a i j k
s
 
        
 

3. A peça rígida mostrada na figura consiste de um
eixo ABC soldado a uma placa retangular DEFH. O conjunto
gira uniformemente a uma velocidade angular de 9 rad/s, em
torno do eixo ABC. Sabendo que o movimento quando visto
de C é anti-horário, determine a velocidade e a aceleração do
vértice F.
Pontos P x y z P(x,y,z)
A 0 0.1 0 (0,0.1,0)
B 0.175 0 0.1 (0.175,0,0.1)
C 0.35 -0.1 0.2 (0.35,-0.1,0.2)
D 0.35 0 0 (0.35,0,0)
F 0 0 0.2 (0,0,0.2)
AC  C  A AC  0.35,0.1,0.20,0.1,0
 
AC  0.35,0.2,0.2

AC  0.35 iˆ 0.2 ˆj  0.2 kˆ


6. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
6
 2 2 2 AC  0.35  0.2  0.2  AC  0.45
 
0.35 ˆ 0.2 ˆ 0.2 ˆ ˆ ˆ
0.45 0.45 0.45
AC
e e i j k
AC
    


eˆ  0.778 iˆ 0.444 ˆj  0.444kˆ
  eˆ  9 0.778 iˆ 0.444 ˆj  0.444 kˆ
 
  7.002 iˆ 3.996 ˆj 3.996 kˆrad s

AF  F  A AF  0,0,0.20,0.1,0
 
AF  0,0.1,0.2
 ˆ AF  0 iˆ 0.1 ˆj  0.2 k

F v   AF
  
v  7.002iˆ 3.996 ˆj 3.996 kˆ0 iˆ 0.1 ˆj  0.2 kˆ

ˆ ˆ ˆ ˆ ˆ
7.002 3.996 3.996 7.002 3.996
0 0.1 0.2 0 0.1
i j k i j
v   
 

0.3996 ˆ 1.4 ˆ 0 7 ˆ F
m
v i j k
s
 
         
 

  F a   F  A  v
   
  0
 
 F  A  0
 
   F     F  A  v
   
ˆ ˆ ˆ ˆ ˆ
7.002 3.996 3.996 7.002 3.996
0.3996 1.4 0.7 0.3996 1.4
F
i j k i j
 v   
    
 
8.39 ˆ 3.304 ˆ 11.399 ˆ F  v   i   j  k
 
 
0
F F a   F  A  v

   

2
8.39 ˆ 3.304 ˆ 11.399 ˆ
m
a i j k
s
 
       
 

4. No problema anterior, use  = 9 rad/s e decresce
à razão de 13.5 rad/s2, encontre a velocidade e aceleração do
vértice H.
5. Sabe-se que a força de atrito estática entre o
bloquinho B e a placa será vencida e o bloco deslizará quando
sua aceleração alcançar 3 m/s2. Se a placa parte do repouso em
t = 0 s e acelera uniformemente à razão de 4 rad/s2, determine
o instante t e a velocidade angular da placa quando o bloco
começar a escorregar; r = 200 mm.
2 2
2 3 R N T R
m
a a a a
s
   
2 4 0.2 0.8 T T T
m
a r a a
s
      
2 2 2 2
2 3 9 0.8 2.891 N T N N
m
a a a a
s
      
2 2.891
3.801
0.2
N
N
a rad
a r
r s
       
0     t
3.801
3.801 0 4 0.95
4
   t t  st  s
6. O bloquinho B repousa sobre a placa horizontal
que gira em torno de um eixo fixo. A placa parte do repouso
em t = 0 e acelera à razão constante de 0.5 rad/s2. Sabendo-se
que r = 200 mm, determinar o módulo da aceleração total do
bloco quando: (a) t = 0 s. (b) t = 1 s e (c) t = 2 s.
2 2
R N T a  a  a
2 0.5 0.2 0.1 T T T
m
a r a a
s
      
0   0rad s
2
0 0 0 N N t  a   ra 
2 0.1 R T R
m
a a a
s
  
t 1
0 0 0.5 1 0.5
rad
t
s
         
2 2
2 1 0.5 0.2 0.05 N N N
rad
t a r a a
s
        
2 0.1 T T
m
a r a
s
   
2 2 2 2
2 0.05 0.1 0.118 R R N T R R
m
a a a a a a
s
       
0 0.1
2 63.43
0.05
T
N
a
tg tg arctg
a
        
t  2 2 0.1 T T
m
a r a
s
   
0 0 0.5 2 1
rad
t
s
         
2 2
2 2 1 0.2 0.2 N N N
rad
t a r a a
s
        
B
A

α
N a

R a

T a



7. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
7
2 2 2 2
2 0.2 0.1 0.2236 R R N T R R
m
a a a a a a
s
       
0 0.1 1
26.56
0.2 2
T
N
a
tg tg arctg
a
   
 
       
 
7. A peça rígida mostrada na figura consiste de um
eixo AB soldado a uma placa retangular DEBC. O conjunto
gira uniformemente a uma velocidade angular constante de 10
rad/s, em torno do eixo AB. Sabendo que o movimento quando
visto de B é anti-horário, determine a velocidade e a
aceleração do vértice E.
Pontos P x y z P(x,y,z)
A 0 0.225 0 (0,0.225,0)
B 0.5 0 0.3 (0.5,0,0.3)
C 0 0 0.3 (0,0,0.3)
D 0 0 0 (0,0,0)
E 0.5 0 0 (0.5,0,0)
AB  B  A AB  0.5,0,0.30,0.225,0
 
AB  0.5,0.225,0.3

AB  0.5 iˆ 0.225 ˆj  0.3 kˆ

 2 2 2 AB  0.5  0.225  0.3  AB  0.625m
 
0.5 ˆ 0.225 ˆ 0.3 ˆ ˆ ˆ
0.625 0.625 0.625
AB
e e i j k
AB
    


eˆ  0.8 iˆ 0.36 ˆj  0.48kˆ
  eˆ 10 0.8 iˆ 0.36 ˆj  0.48 kˆ
 
  8 iˆ 3.6 ˆj  4.8 kˆrad s

BE  E  BBE  0.5,0,00.5,0,0.3
 
BE  0,0,0.3

BE  0 iˆ  0 ˆj 0.3kˆ

E v  BE
  
v  8iˆ 3.6 ˆj  4.8 kˆ0iˆ  0 ˆj 0.3 kˆ

ˆ ˆ ˆ ˆ ˆ
8 3.6 4.8 8 3.6
0 0 0.3 0 0
i j k i j
v   


1.08 ˆ 2.4 ˆ 0 ˆ E
m
v i j k
s
 
       
 

a  E  B  E  B
   
  0
 
 F  A  0
 
   E     E  B  v
   
ˆ ˆ ˆ ˆ ˆ
8 3.6 4.8 8 3.6
1.08 2.4 0 1.08 2.4
E
i j k i j
 v   
 
11.52 ˆ 5.184 ˆ 23.088 ˆ E  v   i   j   k
 
    
0 E
E
v
a   E  B     E  B
 
   
 
2
11.52 ˆ 5.184 ˆ 23.088 ˆ E
m
a i j k
s
 
        
 

8. Atividade 1: Encontre a velocidade e a aceleração
do ponto C considerando que a velocidade angular é 10 rad/s e
decresce a taxa de 20 rad/s2.
9. O rotor de um motor elétrico tem freqüência de
1800 rpm quando é desligado. O rotor pára após executar 625
voltas. Supondo movimento uniformemente retardado, pedem-se:
(a) a aceleração angular do rotor.
(b) o tempo total do movimento.
1800
1800 30
60
f  rpm f  Hz f  Hz
0 0 0 
188.5
2 2 30 60
rad
f
s
          
3926.99
  2 n  2 625 1250 rad
N a

R a

T a



8. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
8

2
2 2 0
0
0
2
2

    

       
 
 2 2
2
4.524
60 3600
1.44
2 1250 2500
rad
s
 
   
  

        
 

0
188.5
0 188.5 4.524 41.67
4.524
    t     t t  t  s
10. Atividade 1: Suponha que um rotor de um motor
execute 2400 rpm em 4 s quando ligado e quando o rotor é
desligado ele retorna ao repouso em 40 s. Assumindo que a
aceleração do movimento é uniforme, determine o número de
voltas dado pelo rotor:
(a) quando é ligado até atingir 2400 rpm.
(b) estando em 2400 rpm, até parar.
11. Na figura, o disco B inicialmente em repouso, é
posto em contato com o disco A que gira inicialmente no
sentido horário com freqüência 450 rpm. Após o contato,
ocorre escorregamento com as superfícies, durante 6 s e
durante os quais, os discos apresentam acelerações angulares
diferentes, mas ambas constantes. Ao término do
escorregamento, o disco A apresenta freqüência constante de
140 rpm. Pedem-se:
(a) as acelerações angulares de cada disco.
(b) a velocidade final do ponto de contato.
Determinando a freqüência angular inicial e final do
disco A:
0 0 0 0
450
2 2 47.12
60 A A A A
rad
f
s
         
140
2 2 14.66
60 Af Af Af Af
rad
f
s
         
Disco A: MCUVR: desacelera de 450 rpm a 140 rpm.
Depois fica com MCU a 140 rpm:
 MCUVR:
2
14.66 47.12
14.66 47.12 6 5.41
6 A A A
rad
s
  

       
 MCU:
14.66 0.08 1.17
PA Af A PA PA
m
v r v v
s
      
Disco B possui os movimentos:
1. Parte do repouso e acelera uniformemente por 6 s.
MCUVA.
2. Mantem movimento uniforme. MCU.
 MCU: Neste segundo movimento, as velocidades
tangenciais de B e A serão iguais:
1.17
PA PB PB
m
v v v
s
  
 MCUVA:
1.17
1.17 0.12
0.12 PB Bf B Bf Bf v   r     
9.75
Bf
rad
s
 
Ou seja, parte do repouso e atinge essa velocidade
angular
Bf  em 6 s:
0
0
f
f
B B
B B B B t
t
 
   

    
2
9.75 0
1.63
6 B B
rad
s
 

  
12. Na polia dupla, ligadas por fios inextensíveis,
suspensos pelos blocos A e B, os fios não escorregam sobre a
polia. O bloco A parte no instante t = 0 s, com aceleração
constante aA = 300 mm/s2 e velocidade inicial vA = 240 mm/s,
ambas de baixo para cima. Determine:
(a) o número de revoluções executadas pela polia em
t = 3 s.
(b) a velocidade e a posição de B em 3 s.
(c) a aceleração do ponto D da polia em t = 0.
 Polia menor:
0.3
0.12
A
A
T
T A A A A
A
a
a r
r
     
2 2.5 A
rad
s
 
0
0 0 0 0
0.24
0.12
A
A A A A A
A
v
v r
r
     
0 2.0
A
rad
s
 
2
0 0
1
2 A A     t    t
2
0 0
1
2 A A       t    t
A
120 mm
B
80 mm

9. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
9
2
0 0
1
2 A A       t    t
2 1
2 3 2.5 3
2
    

2.75
17.25
17.25
2
 rad  rev

    
 Polia maior:
0 0 2.0
A B
rad
s
  
2 2.5 A B
rad
s
  
0 2 2.5 3
B B B B     t   
9.5 B
rad
s
 
9.5 0.18 1.71 B B B B B
m
v r v v
s
       
2
0 0
1
2 B B       t    t
2 1
2 3 2.5 3 17.25
2
       rad
17.25 0.18 3.10571 B B B B s    r s   s  m
 Aceleração em D:
2 2.5
TD D B D A
rad
a r
s
    
2.5 0.18
TD D B TD a   r a    2 0.45
TD
m
a
s

2
0 2
ND D B D A
rad
a r
s
    
2
2 2 0.18 0.72
ND ND
m
a a
s
   
2 2
RD TD ND a  a  a
2 2
2 0.45 0.72 0.849
RD RD
m
a a
s
    
0.45
0.72
D
D
T
N
a
tg tg
a
    
  arctg0.625  32
13. O sistema ilustrado, composto por placas soldadas a
um eixo fixo AB, gira em torno deste, com velocidade angular
 = 5 rad/s, que cresce a taxa de 4 rad/s2. No instante
ilustrado, o ponto C está subindo. Pedem-se:
(a) a velocidade no ponto C.
(c) a aceleração do ponto C.
Pontos x y z (x,y,z)
A 0 0.56 0 (0,0.56,0)
B 0 0 0.8 (0,0,0.8)
C 0.56 0 0 (0.56,0,0)
BA  A BBA  0,0.56,00,0,0.8
 
BA  0,0.56,0.8

BA  0 iˆ  0.56 ˆj 0.8kˆ

 2 2 2 BA  0  0.56  0.8  BA  0.976
 
0 ˆ 0.56 ˆ 0.8 ˆ ˆ ˆ
0.976 0.976 0.976
BA
e e i j k
BA
    


eˆ  0 iˆ  0.573 ˆj 0.819kˆ
Como o ponto C está subindo (horário):
   eˆ  5 0 iˆ  0.573 ˆj 0.819 kˆ
 
  0 iˆ  2.865 ˆj  4.095 kˆrad s

  eˆ  4 0 iˆ  0.573 ˆj 0.819 kˆ
 
  0 iˆ  2.292 ˆj 3.276 kˆ rad s2   

AC  C  A AC  0.56,0,0 0,0.56,0
 
AC  0.56,0.56,0

AC  0.56 iˆ 0.56 ˆj  0 kˆ

C v   AC
  
0 ˆ 2.865 ˆ 4.095 ˆ 0.56 ˆ 0.56 ˆ 0 ˆ C v   i   j   k   i   j   k

ˆ ˆ ˆ ˆ ˆ
0 2.865 4.095 0 2.865
0.56 0.56 0 0.56 0.56
C
i j k i j
v   
 

TD a

ND a

D
RD a


z
x
y
B
A C
0.56 m
0.80 m
0.56 m
D
E

10. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
10
2.293 ˆ 2.2932 ˆ 1.599 ˆ C
m
v i j k
s
 
       
 

C C a   AC  v
    
ˆ ˆ ˆ ˆ ˆ
0 2.292 3.276 0 2.292
0.56 0.56 0 0.56 0.56
i j k i j
  AC   
 
 
  AC 1.8346 iˆ 1.8346 ˆj 1.2835kˆ
 
ˆ ˆ ˆ ˆ ˆ
0 2.865 4.095 0 2.865
2.293 2.293 1.599 2.293 2.293
C
i j k i j
 v   
 
13.97 ˆ 9.389 ˆ 6.569 ˆ C  v    i   j   k
 
C C a   AC  v
    
1.8346 ˆ 1.8346 ˆ 1.2835 ˆ
13.97 ˆ 9.389 ˆ 6.569 ˆ
C a i j k
i j k
      
     

2
12.1354 ˆ 11.2236 ˆ 7.8525 ˆ C
m
a i j k
s
 
        
 

14. O conjunto ilustrado é constituído por um disco
soldado a um eixo vertical e gira no sentido anti-horário a
partir do repouso. A aceleração angular é constante e de valor
α = 1 rad/s2. Um bloco apoia-se no disco a 0.35 m do eixo e
não escorregará em relação ao mesmo até que sua aceleração
total atinja 6.5 m/s2. Pedem-se:
(a) a aceleração 1.0 s após o início do movimento do disco.
(b) o instante que o bloco deslizará.
   ˆj 1 ˆj
 
0 1
0
  ˆj    t ˆj  1 t ˆj
 
            
 
 
  
r  0.35 iˆ

v  r
  
     
ˆ
1 ˆ 0.35 ˆ 1 0.35 ˆ ˆ
k
v t j i v t j i

         
 
v  0.35 t kˆ

 
aT aN
a  r  v
 
    
a  1 ˆj 0.35 iˆ1 t  ˆj 0.35 t  kˆ

   
ˆ ˆ
1 0.35 ˆ ˆ 0.35 ˆ ˆ
k i
a j i t t j k

       

a  0.35kˆ 0.35 t2  iˆa  0.35 t 2  iˆ0.35kˆ
 
  a t 1  0.3512  iˆ 0.35 kˆ

  2
1 0.35 ˆ 0.35 ˆ
m
a t i k
s
 
       
 

0.35 ˆ 0.35 2 ˆ 2 2 T N a    k   t  i a  a  a

   2 2 2 2 2 2 2 0.35 0.35 T N a  a  a a      t
2 4 6.5  0.12250.1225 t
4 42.250.1225  0.1225 t
4
4
42.1275
0.1225 42.1275
0.1225
 t  t 
4 t  343.897 t  4.31s
15. O sistema ilustrado é composto por duas rodas A
e B de raios iguais a 30 mm, que giram em torno de eixos
fixos e por um anel C, encaixado entre as mesmas. O anel tem
raio interno 72 mm e raio externo 76 mm (espessura 4 mm).
Não ocorre escorregamento entre as superfícies de contato. A
roda superior A, gira com freqüência constante f = 400 rpm no
sentido anti-horário. Pedem-se:
(a) a velocidade do anel C;
(b) a velocidade angular da roda inferior B.
(c) as acelerações dos pontos das rodas em contato
com o anel.
6.667
400
400 2 41.887
60 A A A A A
rad
f rpm f Hz f
s
        
ext ext
ext
A
A C A A C C C A
C
r
v v r r
r
       
30
41.887 16.534
76 C C
rad
s
     
int
int int
C
B C B B C C B C
B
r
v v r r
r
       
y
z
B
0.35 m
A
x
ˆj
kˆ
ˆi
B
A
C
x
y
z

11. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
11
72
16.534 39.682
30 B B
rad
s
    
2 ˆ 41.8872 0.03 ˆ
NA A A NA a   r  ja    j
 
2
0 52.635 ˆ
TA RA NA
m
a a a j
s
 
      
 
   
  2 ˆ 39.6822 0.03 ˆ
NB B B NB a   r   j a     j
 
2
0 47.239 ˆ
TB RB NB
m
a a a j
s
 
       
 
   
16. Na figura estão representaas duas engrenagens A
e B, com eixos fixos e com raios rA = 800 mm e rB = 384 mm,
respectivamente. A engrenagem A parte do repouso, acelera
uniformemente no sentido horário e atinge freqüência de
rotação 120 rpm em 5 s, que matém daí por diante. Pedem-se:
(a) a aceleração angular das engrenagens;
(b) a velocidade angular final da engrenagem B;
(c) a velocidade final do ponto pertencente à
engrenagem B, que faz contato com a engrenage, A.
(d) a aceleração do ponto citado no item anterior, nas
mesmas condições.

0
2
120
0 120
60 A A A    f  rpm f  Hz
 12.566
2 4
A A Af
rad
f
s
        
0 12.566 0
5
Af A
A A A t t
  
  
   
    
 
2 2.51 A
rad
s
    o negativo é devido ao sentido horário.
A
A B A A B B B A
B
r
v v r r
r
       
800
12.566 26.17
384 B B
rad
s
    
26.17 ˆ B
rad
k
s

 
   
 


0 26.17 0
5
Bf B
B B B t t
  
  
  
    
 
2 5.236 B
rad
s
  
26.17 0.384 10.049 B B B B B
m
v r v v
s
      
10.049 ˆ B
m
v j
s
 
   
 

0
BT BR BN a  a  a
   
2 2
2
10.049
262.98
0.384 N N N
B
B B B
B
v m
a a a
r s
    
2
262.98 ˆ
BN
m
a i
s
 
   
 

^
17. O sistema ilustrado é formado por uma plca de
dimensões 0.20 x 0. 40 m soldada ao eixo fixo AB; no instante
ilustrado, o sistema gira em torno do eixo fixo com velocidade
angular de 15 rad/s, que decresce a taxa de 7 rad/s2. Quando
obsevada de um ponto B, a placa gira no sentido anti-horário.
Para o instante ilustrado, pedem-se:
(a) a velocidade do ponto C;
(b) a aceleração do ponto C.
Pontos x y z (x,y,z)
A 0 0.1 0 (0,0.1,0)
B 0.4 -0.1 0.2 (0.4,-0.1,0.2)
C 0.4 0 0.2 (0.4,0,0.2)
AB  B  A AB  0.4,0.1,0.20,0.1,0
 
AB  0.4,0.2,0.2

AB  0.4 iˆ 0.2 ˆj  0.2 kˆ

 2 2 2 AB  0.4  0.2  0.2  AB  0.4899
 
0.4 ˆ 0.2 ˆ 0.2 ˆ ˆ ˆ
0.4899 0.4899 0.4899
AB
e e i j k
AB
       


eˆ  0.8165 iˆ 0.4082 ˆj 0.4082kˆ
Anti-horário:
y
x

12. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
12
   eˆ 15 0.8165 iˆ 0.4082 ˆj  0.4082 kˆ
 
 12.2475 iˆ 6.123 ˆj  6.123kˆrad s

  eˆ  7 12.2475 iˆ 6.123 ˆj  6.123 kˆ
 
  85.7325 iˆ  42.861 ˆj  42.861 kˆ rad s2   

AC  C  A AC  0.4,0,0.2 0,0.1,0
 
AC  0.4,0.1,0.2

AC  0.4 iˆ 0.1 ˆj  0.2 kˆ

C v   AC
  
12.2475 ˆ 6.123 ˆ 6.123 ˆ 0.4 ˆ 0.1 ˆ 0.2 ˆ C v  i   j   k   i   j   k

ˆ ˆ ˆ ˆ ˆ
12.2475 6.123 6.123 12.2475 6.123
0.4 0.1 0.2 0.4 0.1
C
i j k i j
v   
 

0.61232 ˆ 0 ˆ 1.225 ˆ C
m
v i j k
s
 
        
 

C C a   AC  v
    
ˆ ˆ ˆ ˆ ˆ
85.7325 42.861 42.861 85.7325 42.861
0.4 0.1 0.2 0.4 0.1
i j k i j
  AC    
 
 
  AC  4.2861 iˆ 0 ˆj 8.571 kˆ
 
ˆ ˆ ˆ ˆ ˆ
12.2475 6.123 6.123 12.2475 6.123
0.61232 0 1.225 0.61232 0
C
i j k i j
 v   
 
 
7.5 ˆ 18.7534 ˆ 3.7492 ˆ C  v    i   j  k
 
C C a   AC  v
    
4.2861 ˆ 0 ˆ 8.571 ˆ
7.5 ˆ 18.7534 ˆ 3.7492 ˆ
C a i j k
i j k
      
     

2
3.2139 ˆ 18.7534 ˆ 12.3202 ˆ C
m
a i j k
s
 
        
 

18. O sistema ilustrado, composto por placas soldadas a
um eixo fixo AB, gira em torno deste, com velocidade angular
constante de  = 5 rad/s. No instante considerado o ponto C
está descendo. Pedem-se:
(a) o vetor velocidade angular.
(b) a velocidade do ponto C na forma vetorial.
(c) a aceleração do ponto C na forma vetorial.
Pontos x y z (x,y,z)
A 0 0.203 0 (0,0.203,0)
B 0 0 0.152 (0,0,0.152)
C 0.178 0.203 0 (0.178,0.203,0)
D 0.178 0 0 (0.178,0,0)
BA  A BBA  0,0.203,00,0,0.152
 
BA  0,0.203,0.152

BA  0 iˆ  0.203 ˆj 0.152kˆ

 2 2 2 BA  0  0.203  0.152  BA  0.254
 
0 ˆ 0.203 ˆ 0.152 ˆ ˆ ˆ
0.254 0.254 0.254
BA
e e i j k
BA
    


eˆ  0 iˆ  0.8 ˆj 0.599 kˆ
  eˆ  5 0 iˆ  0.8 ˆj 0.599 kˆ
 
  0 iˆ  4 ˆj 3 kˆrad s

  eˆ  0
  
AC  C  A AC  0.178,0.203,00,0.203,0
 
AC  0.178,0,0

AD  0.178 iˆ  0 ˆj  0 kˆ

v   AD
  
v  0 iˆ  4 ˆj 3kˆ0.178 iˆ  0 ˆj  0 kˆ

ˆ ˆ ˆ ˆ ˆ
0 4 3 0 4
0.178 0 0 0.178 0
i j k i j
v 

z
x
y
B
A C
0.203 m
0.152 m
0.178 m
D
E

13. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
13
0 ˆ 0.53 ˆ 0.71 ˆ
m
v i j k
s
 
       
 

    C a   C  A    v
    
 C  A  0
 
ˆ ˆ ˆ ˆ ˆ
0 4.0 3 0 4.0
0 0.53 0.71 0 0.53
C
i j k i j
 v  
  
 
4.43 ˆ 0 ˆ 0 ˆ C  v    i   j  k
 
  C C a   C  A  v
   
0 ˆ 0 ˆ 0 ˆ
4.43 ˆ 0 ˆ 0 ˆ
a i j k
i j k
      
     

2
4.43 ˆ
m
a i
s
 
    
 

19. O sistema ilustrado, composto por placas soldadas a
um eixo fixo AB, gira em torno deste, com velocidade angular
constante de  = 5 rad/s. No instante ilustrado, o ponto C está
descendo. Pedem-se:
(a) o vetor velovidade angular.
(b) a velocidade do ponto E na forma vetorial.
(c) a aceleração do ponto E na forma vetorial.
Pontos x y z (x,y,z)
A 0 0.5 0 (0,0.5,0)
B 0 0 0.5 (0,0,0.5)
E 0.4 0.1 0 (0.4,0.1,0)
BA  A BBA  0,0.5,00,0,0.5
 
BA  0,0.5,0.5

BA  0 iˆ  0.5 ˆj 0.5 kˆ

 2 2 2 BA  0  0.5  0.5  BA  0.707
 
0 ˆ 0.5 ˆ 0.5 ˆ ˆ ˆ
0.707 0.707 0.707
BA
e e i j k
BA
    


eˆ  0 iˆ  0.707 ˆj 0.707 kˆ
  eˆ  5 0 iˆ  0.707 ˆj 0.707 kˆ
 
  0 iˆ 3.535 ˆj 3.535 kˆrad s

  eˆ  0
  
AE  E  A AE  0.4,0.1,0 0,0.5,0
 
AC  0.4,0.4,0

AE  0.4 iˆ 0.4 ˆj  0 kˆ

E v   AE
  
0 ˆ 3.535 ˆ 3.535 ˆ 0.4 ˆ 0.4 ˆ 0 ˆ E v   i   j   k   i   j   k

ˆ ˆ ˆ ˆ ˆ
0 3.535 3.535 0 3.535
0.4 0.4 0 0.4 0.4
E
i j k i j
v  
 

1.414 ˆ 1.414 ˆ 1.414 ˆ E
m
v i j k
s
 
        
 

  E E a   E  A  v
   
 E  A  0
 
ˆ ˆ ˆ ˆ ˆ
0 3.535 3.535 0 3.535
1.414 1.414 1.414 1.414 1.414
E
i j k i j
 v  
    
 
10 ˆ 5 ˆ 5 ˆ C  v    i   j   k
 
  E E a   E  A  v
   
0 ˆ 0 ˆ 0 ˆ
10 ˆ 5 ˆ 5 ˆ
E a i j k
i j k
      
     

2
10 ˆ 5 ˆ 5 ˆ E
m
a i j k
s
 
        
 

20. Uma pedra de esmeril, de formato cilíndrico, com
raio R = 0.45 m, gira com freqüência constante f0 = 1800 rpm;
quando se desliga o motor elétrico do esmeril, a pedra gasta 10
s até parar; considerando movimento uniformemente variado,
pedem-se:
(a) a aceleração angular α da pedra;
(b) a velocidade de um ponto P da borda da pedra
quando a freqüência é 1800 rpm;
(c) a aceleração de um ponto P da borda da pedra,
quando a freqüência é 1800 rpm.
z
x
y
B
A C
0.4 m
0.1 m
G D
0.1 m
0.4 m
0.2m
0.2m
D E
F

14. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
14
30
0 0
1800
1800 2 188.5
60
rad
f rpm f Hz f
s
        
0 0 188.5
t t 10
  
  
  
    
 
2 18.85
rad
s
   
188.5 0.45 84.82 P P P
m
v r v v
s
      
2 2
2 188.5 0.45 15989.1
PN PN PN
m
a r a a
s
      
0 é cte
PT a  
PR PN PT PR PN a  a  a a  a
    
21. Dois discos de raios RB = 45 mm e RA = 20 mm
estão em contato sem escorregar.
O disco A(inferior) parte do repouso e acelera de
forma uniforme com aceleração αA = 3 rad/s2. Para o instante
em que a velocidade angular do disco A atinge valor A = 20
rad/s, pedem-se:
(a) a aceleração angular do disco B.
(b) a velocidade angular do disco B.
(c) a velocidade de um ponto na borda do disco B.
(d) a aceleração de um ponto na borda do disco B.
Disco A: MCUVA:
A A0 A     t

6.67
20
20 0 3
3
   t t  s
Disco B:
A
A B A A B B B A
B
R
v v R R
R
       
20
20 8.89
45 B B
rad
s
    
B B0 B     t
 2
1.33
8.89
8.89 0 6.67
6.67 B B
rad
s
    
20 0.02 0.4 A A A A A B
m
v R v v v
s
       
2 1.33 0.045 0.05985
BT B B BT BT
m
a R a a
s
      
2 2
2
0.4
3.55
0.045 N N N
B
B B B
B
v m
a a a
R s
    
2 2
BR BN BT BR BN BT a  a  a a  a  a
  
2 2
2 3.55 0.05985 3.56
BR BR
m
a a
s
   
22. O disco de raio R = 80 mm parte do repouso e
acelera de maneira uniforme, atingindo a velocidade angular 
= 30 rad/s em 10 voltas. Pedem-se:
(a) a aceleração angular do disco;
(b) o tempo gasto nessas 10 voltas iniciais.
Disco: MCUVA:
2
0
1
2
   t    t

62.832
  2 10  20 rad
2 2 2 2
0    2  30  0  2 62.831
2
2
30
7.16
2 62.831
rad
s
   

0     t30  07.16 t
z
y
R
x
A
PB
B
PA
80 mm

15. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
15
30
4.19
7.16
t  t  s
22. A haste ABCD gira apoiada nas articulações A e
D; no instante ilustrado, a velocidade angular da barra é 95
rad/s, que decresce à taxa de 380 rad/s2. E o ponto C está
subindo. Pedem-se:
(a) a velocidade do ponto B, para o instante ilustrado;
(b) a aceleração do ponto B, no instante ilustrado.
Pontos x y z (x,y,z)
A 0 0.2 0.12 (0,0.2,0.12)
B 0.3 0.2 0.12 (0.3,0.2,0.12)
D 0.3 0 0 (0.3,0,0)
DA  ADDA  0,0.2,0.120.3,0,0
 
DA  0.3,0.2,0.12

DA  0.3 iˆ  0.2 ˆj  0.12 kˆ

 2 2 2 DA  0.3  0.2  0.12  DA  0.38
 
0.3 ˆ 0.2 ˆ 0.12 ˆ ˆ ˆ
0.38 0.38 0.38
DA
e e i j k
DA
        


eˆ  0.789 iˆ  0.5263 ˆj  0.3158 kˆ
Anti-horário:
   eˆ  95 0.789 iˆ  0.5263 ˆj  0.3158 kˆ
 
  75 iˆ 50 ˆj 30 kˆrad s

  eˆ  380 75 iˆ 50 ˆj 30 kˆ
 
  28500 iˆ 19000 ˆj 11400kˆ rad s2   

AB  B  A AB  0.3,0.2,0.120,0.2,0.12
 
AB  0.3,0,0

AB  0.3 iˆ  0 ˆj  0 kˆ

B v   AB
  
 75 ˆ 50 ˆ 30 ˆ 0.3 ˆ 0 ˆ 0 ˆ B v   i   j   k   i   j   k

ˆ ˆ ˆ ˆ ˆ
75 50 30 75 50
0.3 0 0 0.3 0
B
i j k i j
v  

0 ˆ 9 ˆ 15 ˆ B
m
v i j k
s
 
       
 

B B a   AB  v
    
ˆ ˆ ˆ ˆ ˆ
28500 19000 11400 28500 19000
0.3 0 0 0.3 0
i j k i j
  AB    
 
  AB  0 iˆ 3420 ˆj 5700kˆ
 
ˆ ˆ ˆ ˆ ˆ
75 50 30 75 50
0 9 15 0 9
B
i j k i j
 v   

 
1020 ˆ 1125 ˆ 675 ˆ B  v    i   j   k
 
B B a   AB  v
    
0 ˆ 3420 ˆ 5700 ˆ
1020 ˆ 1125 ˆ 675 ˆ
B a i j k
i j k
      
     

2
1020 ˆ 4545 ˆ 5025 ˆ B
m
a i j k
s
 
        
 

23. O sistema de engrenagens ilustrado, deve
suspender o bloco alçando-o por 6.10 m. A engrenagem A
parte do repouso e, mantendo aceleração angular constante,
atinge a freqüência de 120 rpm em 5 s, mantendo-se constante
após atingí-la. Pedem-se:
(a) o número de rotações da engrenagem;
(b) o tempo gasto na operação.
 Engrenagem A:
A
D
z
x
300 mm
200 mm
C 120 mm
B
76.2
381
76.2
457
Em mm
B A

16. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
16
0
120
0 2 2
60 A A A       f    
12.566 A
rad
s
 
2
12.566
2.513
5 A A A
rad
t s

  

    

A
A B A A B B B A
B
r
v v r r
r
       
0.0762
12.566 2.095
0.457 B B
rad
s
    
N o MUV o  de B percorrido em 5s será:
2 2
0 2 B B     
2 2 2 2
0 2.095 0
2 2 0.419 B
 
 

 
    
 
0
5.2375
B iB   rad s  r 
0 0
0.381 5.2375 2 B B s   s  m
6.1
0.381 i
i
B
B B B B B
B
s
s r
r
     
16.01 B   rad
2
2.095
0.419
5 B B B
rad
t s

  

    

Faltam:
0
6.1 6.1 2 4.1 B s    m
Nesses 4.1 m a engrenagem B percorre em
velocidade angular constante; o tempo gasto será de:
4.1
2.095 0.381
B B Bi
s
v r
t t


     
 
4.1
5.1365
2.095 0.381
t  t  s

A polia A gastará 5 s em MUVA e 5.1365 s em MU:
12.566 A
rad
s
 
12.566 5.1365 A A A   t  
64.546
AMU   rad
Em MUV:
0
2 1
2 AMUV A A    t    t
2 1
0 2.513 5 31.4125
2 AMUV AMUV   t     rad
64.546 31.4125
AMU AMUV    
95.9585
AMU AMUV     rad
95.9585
2 2
AMU AMUV rev
 
 
  

15.27
2
AMU AMUV rev
 

  

5 5.1365 T MUV MU t  t t    10.1365 T t 
24. A polia ilustrada na figura possui raio R = 0.32 m
e é acionada por um motor elétrico, com o intuito de
suspender o bloco A. Quando a polia apresenta freqüência de
rotação f0 = 120 rpm, o motor é desligado. Mesmo assim, o
bloco ainda sobe h = 0.80 , antes de parar. Pedem-se:
(a) a aceleração angular da polia;
(b) o tempo gasto até parar.
0 0 0
120
2 2 12.566
60
rad
f
s
         
0.8
2.5
0.32
h
h R rad
R
        
2 2
2 2 0
0 2
2
F
F
 
    


      
 
2 2
2
0 12.566
31.58
2 2.5
rad
s
 

   

0     t0 12.56631.58 t
12.566
0.397
31.58
t  t  s
25. A figura figura ilustra uma correia que move-se
entre duas polias A e B, de raios RA = 0.06 m e RB = 0.02 m,
respectivamente, sem que ocorra escorregamento entre as
superfícies em contato. A velocidade da correia aumenta
uniformemente, desde v1 = 0.8 m/s até v2 = 2.4 m/s, em 5 s.
Pedem-se: (a) a aceleração angular de cada polia; (b) o
número de voltas efetuadas por cada uma das polias, nos 5 s.
R A
RA

17. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
17
2.4 0.8
0.32
5 c c c
v m
a a a
t s
 
    

A
c A A A A A
A
a
a a a R
R
     
2
0.32
5.33
0.06 A A
rad
s
   
B
c B B B B B
B
a
a a a R
R
     
2
0.32
16
0.02 B B
rad
s
   
B
B B B B
B
v
v R
R
   
2.4
120
0.02 B B
rad
s
   
0
0 0 0
B
B B B B
B
v
v R
R
   
0 0
0.8
40
0.02 B B
rad
s
   
0
0
2 2
2 2 2
2
B B
B B B B B
B
 
    


       

2 2 120 40
400
2 16 B B   rad

    


63.7
400
2 B  rev

 
A
A A A A
A
v
v R
R
   
2.4
40
0.06 A A
rad
s
   
0
0 0 0
A
A A A A
A
v
v R
R
   
0 0
0.8
13.33
0.06 A A
rad
s
   
0
0
2 2
2 2 2
2
A A
A A A A A
A
 
    


       

2 2 40 13.33
133.42
2 5.33 A A   rad

    

21.2
133.42
2 A  rev

 

26. Uma polia dupla, de raios R1 = 1.5 m e R2 = 0.8
m, gira sob ação de dois blocos A e B, conforme ilustrado. O
bloco A apresenta aceleração aA = 4 m/s², com velocidade
inicial (em t = 0 s), vA0 = 5 m/s. Considerando o intervalo de
tempo de 2 s, pedem-se:
(a) o número de voltas da polia;
(b) as correspondentes velocidade e percurso do
bloco B;
(c) a aceleração centrípeta de um ponto da borda mais
externa da polia (R1 = 1.5 m).
0
5 4 2 13 A A A A A
m
v v a t v v
s
        
1
1
A
A A A
v
v R
R
   
13
8.667
1.5 A A
rad
s
   
0
0 0 1 0
1
A
A A A
v
v R
R
   
0 0
5
3.33
1.5 A A
rad
s
   
1
1
A
A A A
a
a R
R
   
2
4
2.67
1.5 A A
rad
s
   
0
0
2 2
2 2 2
2
A A
A A A A A
A
 
    


       

v
RB v
R2 R1

18. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
18
2 2 8.667 3.33
11.99
2 2.67 A A   rad

    

11.99
1.91
2 A A  rev  rev

    
2 8.667 0.8 B B B v  R v  
6.93 B
m
v
s

B0 B0 2 B0 B0 2 v  R v  R
0 0
3.33 0.8 2.664 B B
m
v v
s
   
2 2.67 0.8 B B B a  R a  
2 2.136 B
m
a
s

0
0
2 2
2 2 2
2
B B
B B B B B
B
v v
v v a s s
a

       

2 2 6.93 2.664
9.58
2 2.136 B B s s m

    

0
2 2
2
1
5
16.67
1.5 A A A
A
cp cp cp
v m
a a a
R s
    
27. As engrenagens ilustradas A, B e C, tem
respectivamente raios RA = 0.24 m, RB = 0.16 m e RC = 0.32 m
e apresentam eixos fixos. A engrenagem A gira com
velocidade angular constante A = 5 rad/s, no sentido horário.
Pedem-se:
(a) as velocidades angulares das engrenagens B e C;
(b) a aceleração de um ponto periférico da
engrenagem A.
2 7.50 3.75 ; 4.5 B C
rad rad m
a
s s s
    
 Exercícios
1. Uma polia está conectada por cabos inextensíveis
conforme mostra a figura. O movimento da polia é
controlado pelo cabo C o qual tem uma aceleração constante
de 9 in/s2 e uma velocidade inicial de 12 in/s, ambas para a
direita.Determine:
(a) o número de revoluções executados pela polia em 2 s.
(b) a velocidade e a mudança na posição do corpo B após
2s. (c) a aceleração do ponto D da polia interior no instante t
= 0s.
 Solução:
0 0 0 0 12 3 4 D v  r       rad s
2 9 3 3
t D a  r       rad s 
 
1
14 2.23 rev
2
rev
rad
 rad
 
  
 
0     t  432 10rad s
2 2
0
1 1
4 2 3 2 14
2 2
   t    t        rad
5 10 50 B B B v  r  v   v  in s
5 14 70 B B B y  r  y   y  in 
  2 9 D t C
a  a  in s 
 
      2 2 2
0 3 4 48 D n D D n D n
a  r   a    a  in s 
48 48
tan arctan 79.4
9 9
      
2
48
79.4 48 48.8
79.4 D D D
in
a sen a a
sen s
      

RB
RA
RC

19. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
19
2. O movimento de um corpo é dado por:
    3 2  t  t 9 t 15 t SI .
Determine a posição angular, a velocidade angular e
a aceleração angular nos instantes:
(a) t = 0 s (b) t =3s.
3. No problema anterior, determine a posição angular
e a aceleração nos instantes em que a velocidade angular se
anula.
4. A cinta conecta as rodas do auto. O eixo B possui
aceleração angular constante de 120 rad/s2 em sentido anti-horário,
Ela está inicialmente em repouso, Determine a
aceleração da cinta no ponto C, quando:
(a) t = 0.5 s (b) t = 2s.
5. Uma série de componentes pequenos estão
sendo movidos por um transportador. O cinto passa por
uma polia tensora de 6 in de raio. No instante mostrado,
a velocidade do ponto A é 15 in/s para a esquerda e sua
aceleração vale 9 in/s2 para a direita.
Determinar:
(a) a velocidade angular e aceleração angular
da polia,
(b) a aceleração total da máquina
componente em B.
15
2.5
6
B
B B B B
v rad
v r
r s
       
2
9
1.5
6
B
B
T
T
a rad
a r
r s
       
2 2
2
15
37.5
6 B B B
B
N N N
v in
a a a
r s
    
2 2
B NB TB a  a  a
2 2 37.5 9 B a  
2 38.6 B
in
a
s

37.5
tan tan
9
B
B
N
T
a
a
    
0 37.5
arctan 76.5
9
   
6. A vara dobrada ABCDE gira sobre uma linha que
une os pontos A e E com uma velocidade angular constante de
9 rad/s. Sabendo que a rotação observada do ponto E é no
sentido horário, determine a velocidade e a aceleração de C.
Obs.:
ˆ
AE
AC CE AE e
AE
   

  

  eˆ

  AC
    AC  AE CE
    
EC  CE
 
 
0 pois AE
AC AE EC AE EC

         
  

        

  AC  EC
   
Logo, tanto faz escolher o ponto A ou E!!!
A (0,0.4,0.2); C(0,0.15,0); E(0.4,0,0)
AC r  C  A

(0,0.15,0) (0,0.4,0.2) AC r  

0 ˆ 0.25 ˆ 0.2 ˆ AC r   i   j   k

ˆEA
EA
n
EA



EA  A EEA  0,0.4,0.20.4,0,0
 
AE  0.4 iˆ  0.4 ˆj  0.2kˆ

 2 2 2 AE  0.4  0.4  0.2  AE  0.6
 
0.4 ˆ 0.4 ˆ 0.2 ˆ ˆ
0.6 0.6 0.6 AE n    i   j   k

B
TB a

NB a


20. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
20
ˆEA   n

0.4 ˆ 0.4 ˆ 0.2 ˆ 9
0.6 0.6 0.6
 i j k
 
       
 

  6 iˆ  6 ˆj 3 kˆ

Cv  r
  
 6 ˆ 6 ˆ 3 ˆ 0 ˆ 0.25 ˆ 0.2 ˆ C v    i   j   k   i   j   k

ˆ ˆ ˆ ˆ ˆ
6 6 3 6 6
0 0.25 0.2 0 0.25
C
i j k i j
v   
  

6  0.2  0.25 3 ˆ 1.2 ˆ 6  0.25 ˆ C v        i   j     k

0.45 ˆ 1.2 ˆ 1.5 ˆ  C v    i   j   k m s

C C a  v
  
ˆ ˆ ˆ ˆ ˆ
6 6 3 6 6
0.45 1.2 1.5 0.45 1.2
C
i j k i j
a   
   

12.6 ˆ 7.65 ˆ 9.9 ˆ 2 C a   i   j   k m s 

7. A aceleração angular de um disco oscilando é
definida pela relação:
  k 
Determine:
(a) o valor de k para o qual  = 8 rad/s quando  = 0
e  = 4 rad quando  = 0.
(b) a velocidade angular do disco quando  = 3 rad.
(a) 4 s-2 (b) 5.29 rad/s
8. Resolva o problema 2 encontrando a posição
angular e a aceleração angular quando a velocidade angular
for nula.
9. No problema 6, determine a velocidade e a
aceleração do ponto B. Assuma que a velocidade angular é 9
rad/s e aumenta a uma taxa de 45 rad/s2.
10. A Terra faz uma volta completa a cada 23h e 56
min. Sabendo que o seu raio é 3960 mi, determine a
velocidade linear e a aceleração linear em um ponto sobre o
equador.
11. O anel C possui raio interno de 55 mm e raio
externo de 60 mm e está posicionado entre duas rodas A e B,
cada uma de raio externo de 24 mm. Sabendo que a roda A
gira com freqüência 300 rpm e que não ocorre deslizamento,
determine:
(a) a velocidade angular do anel C e da roda B.
(b) a aceleração dos pontos A e B que estão em
contato com C.
A A A v   r
A Cext C Cext v  v   r
2 2
A A C Cext A A C Cext   r   r    f  r    f  r
300 24
120 rpm
60
ext
A A
C C C
C
f r
f f f
r
 
    
int int
2 2 B B C C B B C C   r   r    f  r    f  r
int 120 55
275 rpm
24
C C
B B B
B
f r
f f f
r
 
    
2
2 A
A A A A
A
v
a r a
r
   
300
2 2 0.024
60 A A A A v    f  r v    
0.754 A
m
v
s

2
2
0.754
23.7
0.024 A A
m
a a
s
   
275
2 2 0.024
60 B B B B v    f  r v    
0.6911 B
m
v
s

2
2 B
B B B B
B
v
a r a
r
   
2
2
0.6911
19.9
0.024 B B
m
a a
s
   
12. Um cilindro A está se movendo para baixo a uma
velocidade de 9 ft/s quando um breque é aplicado
repentinamente no tambor. Sabendo que o cilindro se move 18
ft para baixo antes de parar, e, assumindo movimento com
aceleração uniforme, determine:
(a) a aceleração angular da roda.
(b) o tempo que leva para o cilindro parar.

21. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
21
9
12
0.75
A
A A A A A A
A
v rad
v r
r s
       
2 2
0    2 
18
24 rad
0.75
s
s r
r
       
2
2 2
2
12
0 12 2 24 3
48
rad
s
        
2
0 0
1
2
    t    t
2 1
24 0 12 3
2
   t   t
2 2 3 t 24t  48  0t 8 t 16  0
2 4 8 64 64
4
2 2
b b a c
t t t s
a
      
    

13. Uma polia e dois pesos são conectados por uma
corda inextensível. O peso A tem uma aceleração constante de
300 mm/s2 e uma velocidade inicial de 240 mm/s, ambos
dirigidos para cima. Determine:
(a) o número de revoluçõe executados pela polia em 3 s.
(b) a velocidade e a posição do peso B após 3s.
(c) a aceleração do ponto D na borda da polia, em t = 0s.
14. Uma chapa circular está inicialmente em repouso.
Sabendo que r = 200 mm e que a placa possui aceleração
angular constante de 0.3 rad/s2, determine a magnitude da
aceleração total no ponto B quando:
(a) t = 0, (b) t = 2 s, (c) t = 4 s.
15. O anel B tem um raio interno r2 e externo r3. A
barra A de raio r1 gira com velocidade angular constante A.
Não há escorregamento entre as superfícies. Determine as
relações entre os raios r1, r2, r3 e A para: (a) a velocidade
angular do anel B; (b) a aceleração dos pontos entre a barra A
e o anel B que estão em contato.
16. Um disco circular de raio r = 0.16 m gira em
relação a um eixo fixo O com velocidade angular  = 2 rad/s e
aceleração angular  = 3 rad/s2 com sentidos indicados na
figura. Determine os valores instantâneos da velocidade e da
aceleração no ponto A da figura.
A
O  x
y
4
r
r

22. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
22
cos ˆ ˆ A r OA  r    i  r  sen  j
 
2 1
cos 1 cos
4
  sen   
2
1
1
4
sen
 
   
 
15
0.968
4
sen  sen 
0.25 ˆ 0.968 ˆ A r  r   i  r   j

0.16 0.25 ˆ 0.16 0.968 ˆ A r    i    j

0.04 ˆ 0.15488 ˆ A r   i   j

  kˆ  2kˆ
 
A A v  r
  
2 ˆ 0.04 ˆ 0.15488 ˆ A v    k   i   j

   
   
ˆ ˆ
2 0.04 ˆ ˆ 2 0.15488 ˆ ˆ A
j i
v k i k j

          


0.08 ˆ 0.30976 ˆ 0.30976 ˆ 0.08 ˆ A A v    j   i v    i   j
 
  kˆ  3 kˆ
 

A A A a  r  v
    
3 ˆ 0.04 ˆ 0.15488 ˆ A a   k   i   j

2 kˆ0.30976 iˆ 0.08 ˆj 
0.12 ˆ ˆ 0.4646 ˆ ˆ A a   k i   k  j

ˆ ˆ ˆ ˆ 0.6194 k i  0.16 k  j
0.12 ˆ 0.4646  ˆ A a   j   i

0.6194 ˆj  0.16 iˆ
0.12 ˆ 0.4646 ˆ A a   j   i

ˆ ˆ 0.6194 j 0.16 i
0.3046 ˆ 0.739 ˆ A a   i   j

17. Para testar a resistência de um adesivo, é
colocado um bloco de massa m = 0.3 kg em um disco que gira
a partir do repouso em t = 0 s com aceleração angular
uniforme  = 2 rad/s2. Se a fita se solta depois de 3 s do
movimento do disco, quantas voltas o disco execuitará?
18. A correia acoplada ao conjunto de polias faz girar
o sistema aumentando sua velocidade angular. Num certo
instante, a velocidade da correia é 1.5 m/s e a aceleração total
do ponto A é 75 m/s2.Para esse instante, determine:
(a) a velocidade angular e a aceleração angular da
polia B. (b) a aceleração total do ponto B.
(c) a aceleração do ponto C.
19. O ponto A da polia está na posição angular  = 0
em t = 0s. O disco tem velocidade angular inicial 0 = 0.1
rad/s em t = 0 e é acelerado com uma aceleração angular
constante  = 2 rad/s2. Determine a velocidade e a aceleração
do ponto A, no instante t = 1 s, em função dos vetores
unitários ˆi e ˆj
.
20. Uma fita magnética utilizada para gravar dados
em um computador consiste no sistema indicado.
Se a velocidade v da fita é constante e a magnitude da
aceleração do ponto A é 4/3 a aceleração do ponto B,
determine o raio de A.
21. As características de um sistema de engrenagens
é ilustrado a seguir:

23. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
23
A engrenagem B está girando no sentido horário, com 300 rev/min, quando um torque é aplicado na engrenagem A, em t = 2 s, forçando-a a girar no sentido anti-horário com uma aceleração angular  que varia com o tempo conforme o gráfico indicado, durante 4 s. Determine a velocidade da polia B, quando t = 6 s.
23. A potência de um motor elétrico quando ligado o faz girar a 3300 rpm em 6 s, e quando é desligado ele retorna ao repouso em 80 s. Assumindo aceleração uniforme, determine o número de revoluções dado pelo motor quando:
(a) é ligado e atinge a máxima rotação;
(b) é desligado a partir da máxima rotação até atingir o repouso.
24. Assumindo que a Terra gira em torno de seu eixo em 23h e 56 min e seu raio é aproximadamente 6400 km, determine a velocidade de rotação sobre um ponto da superfície do Equador. E num ponto na latitude de 400 N?
25. No sistema de polias abaixo, o disco B está em repouso quando é colocado em contato com o disco A que está girando no sentido horário a 450 rpm. Após 6 s de deslizamento, cada disco tem uma aceleração angular constante e o disco A possui uma freqüência de 140 rpm no sentido horário. Determine a aceleração angular de cada disco durante o período de deslizamento.
 Movimento Plano Geral
Um movimento plano geral pode ser considerado como a soma de uma translação e de uma rotação:
Movimento geral = Translação + Rotação

24. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
24
Movimento de um corpo decomposto em uma
translação e uma rotação:
 Velocidade absoluta e relativa:
B A B/A v  v  v
  
: B v

velocidade absoluta do ponto B.
: A v

translação da placa com A.
/ : B A v

velocidade relativa associada à rotação da
placa ao redor do ponto A, medida em relação a eixos com
origem em A e de orientações fixas. Denotando por :
/ : B A r

vetor de posição de B em relação a A:
B/A r  B  A

  kˆ : velocidade angular em relação aos eixos de
orientações fixas.
/ /
ˆ
B A B A v   k r
 
/
ˆ
B A B A v  v  k r
  
Movimento plano = Translação com A + Rotação em torno de A.
Observe que:
/
/
B A
B A B A
v
v v tg v l
l
       
/
/
cos
cos
A A
B A
B A
v v
v
v


  
cos
A v
l




Chega-se ao mesmo resultado escolhendo B como
pono de referência. Decompondo-se o movimento dado em
uma translação com B e uma rotação ao redor de B (vide
figura), teremos:
Movimento plano = Translação com B + Rotação em torno de B.
A B A/B v  v  v
  
Observe que:
A/B B/A A/B B/A v  v  v  v  l 
   
O sentido da velocidade relativa deponde do ponto de
referência escolhido e deverá ser cuidadosamente determinada
a partir dos diagramas ilustrados. Finalmente, observemos que
a velocidade angular  da barra em sua rotação ao redor de B
é a mesma que em sua rotação ao redor de A. Em ambos os
casos é medida pela derivada temporal do ângulo :
d
dt

   
Este resultado é geral; assim, sempre a velocidade
angular  de um corpo rígido animado de movimento
plano é independente do ponto de referência.
A maior parte dos mecanismos mecânicos constam
não de um, mas de vários elementos em movimento. Quando
tais elementos se encontram articulados, pode-se estudá-los
considerando cada um como um corpo rígido, sem, contudo,
esquecer que os pontos de articulação de dois deles devem ter
a mesma velocidade absoluta. Um estudo semelhante pode ser
feito quando se trata de engrenagens, já que os dentes em
constato devem ter a mesma velocidade absoluta. Entretanto,
se os elementos de um mecanismo possuem um deslizamento
relativo entre si, deve-se levar em consideraçãoa velocidade
relativa das partes em contato.

25. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
25
 Exemplos resolvidos
1. A engrenagem dupla mostrada na figura rola sobre
a cremalheira inferior estacionária; a velocidade do seu centro
A é de 1.2 m/s para a direita. Determinar:
(a) a velocidade angular da engrenagem,
(b) as velocidades da cremalheira superior R e do
ponto D da engrenagem.
Como a engrenagem rola sobre a cremalheira
inferior, seu centro A percorrerá uma distância igualao
comprimento da circunferência exterior, 2r1, para cada
rotação completa da engrenagem. Como 1 ver = 2 rade,
quando A rola para a direita, (xA > 0), a engrenagem gira em
sentido horário ( < 0), escrevemos:
A 1 x  r 
1 1
A
A
dx d
r v r
dt dt

      
1
1.2
8
0.150
A v rad
r s
        
ˆ 8 ˆ
rad
k k
s
      
 
O rolamento é decomposto em dois movimentos: um
de translação do centro A e outro de rotação ao redor deste
centro. Na translação, todos os pontos da engrenagem
deslocam-se com a mesma velocidade va. Na rotaça, cada
ponto P da engrenagem se desloca ao redor de A com
velocidade:
P AP v  r
  
AP r  P  A

Aqui PA r

é o vetor de posição de P em relação a A.
Assim, a velocidade da cremalheira superior é a
velocidade do ponto B:
R B B A AB v  v v  v v
    
B A AB v  v  r
   
1.2 ˆ  8 ˆ 0.1 ˆ B v   i    k   j

ˆ
1.2 ˆ 0.8 ˆ ˆ
i
B v i k j

    

1.2 ˆ 0.8 ˆ 2.0 ˆ B B
m
v i i v i
s
 
        
 
 
Velocidade do ponto D:
D A AD v  v  r
   
1.2 ˆ  8 ˆ  0.15 ˆ D v   i    k    i

 
ˆ
1.2 ˆ 8 0.15 ˆ ˆ
j
D v   i    k i

1.2 ˆ 1.2 ˆ D
m
v i j
s
 
     
 

2 2 1.2 1.2 2.88 1.7 D D
m
v v
s
 
      
 
 
tan 1  45
1.2 ˆ 1.2 ˆ 1.7 45 D D
m m
v i j v
s s
   
         
   
 
2. No sistema esboçado, a manivela AB possui uma
velocidade angular constante de 2000 rpm (freqüência f) no
sentido horário. Determinar para a posição da manivela
indicada na figura:
(a) a velocidade angular da biela BD.
(b) a velocidade do pistão P.
1 100
2000 2000
60 3
f  rpm f  Hz f  Hz
200
2 209.45
3
rad rad
f
s s

      
0.0762 209.45 AB AB AB v  r  v  

26. Cinemática dos Sólidos – Prof. Cláudio S. Sartori
Notas de aula 01 – 1° Bimestre
26
0 15.95 50 AB
m
v
s
  
Movimento da Biela BD:
Aplicando a lei dos senos:
40 40
0.0762
0.0762 0.203 0.203
sen sen sen
sen


 
   
sen  0.241  arcsen0.241 13.96
Observe que a velocidade vD do ponto D, onde a biela
se une ao pistão, deve ser horizontal. Decompondo o
movimento de BD:
Movimento plano de BD= Translação + rotação
D B DB v  v  v
  
Fazendo o diagrama vetorial dessa relação:
53.9 50 76.1
D DB B v v v
sen sen sen
 
  
15.9 15.9
50
53.9 50 76.1 76.1
D DB
DB
v v
v sen
sen sen sen sen
    
   
12.5 DB
m
v
s
 
  
 
76.1°
15.9
53.9 13.2
76.1 D D
m
v sen v
sen s
    
