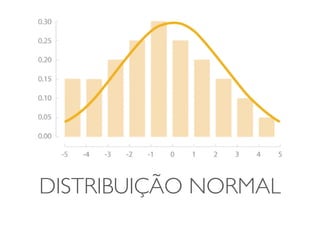
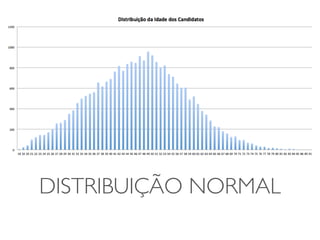
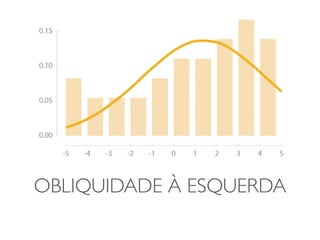
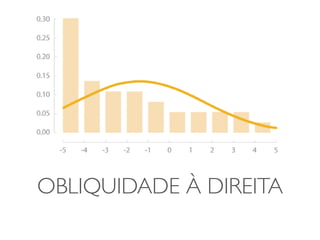
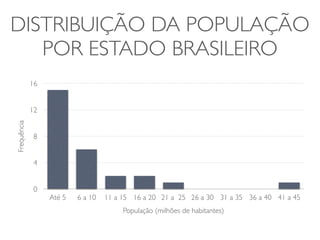
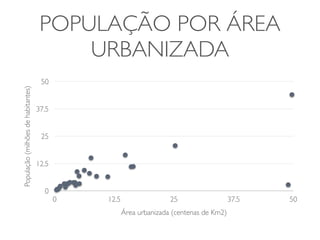
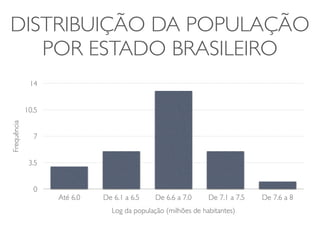
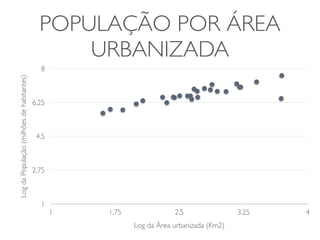
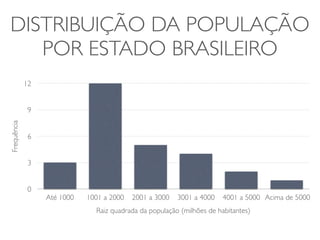
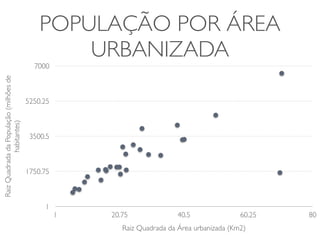
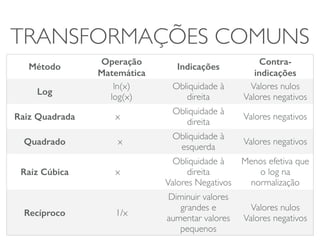
O documento discute transformações de dados para corrigir imperfeições e tornar os dados mais adequados para análises estatísticas. Ele explica que transformações como logaritmo, raiz quadrada e quadrado podem ser usadas para ajustar a distribuição dos dados e torná-los mais simétricos. O documento fornece exemplos dessas transformações em conjuntos de dados reais e alerta sobre os cuidados necessários na interpretação dos resultados transformados.

1. TRANSFORMAÇÃO DE DADOS
Alexandre Duarte - http://alexandre.ci.ufpb.br/ensino/iad

2. TRANSFORMAÇÃO DE
DADOS
• Quando tiramos uma foto muitas vezes o resultado não é o esperado
• As cores podem estar muito escuras ou muito claras
• O foco pode estar errado
• Objetos podem estar muito pequenos
• Nestes casos, utilizamos ferramentas para aplicar filtros e transformar
a foto em algo mais próximo do que desejamos
• Muitas vezes o mesmo ocorrer com os dados

3. TRANSFORMAÇÃO DE
DADOS
• Muitas vezes obtemos um conjunto de dados que quando
visualizado apresenta imperfeições ou objetivos difíceis de ver
• Além disso, se você pretende analisar estatisticamente seus
dados provavelmente precisar considerar a forma como os
dados estão distribuídos
• Transformações são utilizadas para tratar destes dois
problemas

4. TRANSFORMAÇÃO DE
DADOS
• Transformações são conjuntos de procedimentos
de manipulação que podem revelar fatos não
observáveis em sua forma original.
• Podemos, por exemplo, ajustar a distribuição dos
dados para torná-los mais fáceis de exibir e
adequadas para certos testes estatísticos

5. ALERTA
• Jamais realize operações de transformação em
seus dados originais!
• Você deve criar uma nova coluna para armazenar
os novos valores para as variáveis sendo
transformadas ou criar uma cópia inteira do seu
conjunto de dados!

6. DISTRIBUIÇÃO NORMAL
• Uma das suposições mais frequentemente utilizadas nos testes
estatísticos é que os dados são normalmente distribuídos
• Os dados se distribuem de foram simétrica ao redor de um
valor central
• “Curva do sino”
• Alguns dados que são geralmente geralmente distribuídos de
forma normal são medições humanas como altura, peso,
expectativa de vida e resultados em testes de QI

7. DISTRIBUIÇÃO NORMAL

8. DISTRIBUIÇÃO NORMAL

9. OBLIQUIDADE
• Dados oblíquos, diferentemente de dados normais, não se
distribuem de forma simétrica em relação a um valor central.
• Estes conjuntos tendem a ter mais observações à direita ou
à esquerda deste valor
• Se você observar que seus dados apresentam esta
característica talvez seja necessário realizar algum tipo de
transformação

10. OBLIQUIDADE À ESQUERDA

11. OBLIQUIDADE À DIREITA

12. EXEMPLO

13. DISTRIBUIÇÃO DA POPULAÇÃO
POR ESTADO BRASILEIRO
Frequência
16
12
8
4
0
Até 5 6 a 10 11 a 15 16 a 20 21 a 25 26 a 30 31 a 35 36 a 40 41 a 45
População (milhões de habitantes)

14. POPULAÇÃO POR ÁREA
URBANIZADA
População (milhões de habitantes)
50
37.5
25
12.5
0
0 12.5 25 37.5 50
Área urbanizada (centenas de Km2)

15. TRANSFORMAÇÃO
LOGARÍTMICA

16. DISTRIBUIÇÃO DA POPULAÇÃO
POR ESTADO BRASILEIRO
Frequência
14
10.5
7
3.5
0
Até 6.0 De 6.1 a 6.5 De 6.6 a 7.0 De 7.1 a 7.5 De 7.6 a 8
Log da população (milhões de habitantes)

17. POPULAÇÃO POR ÁREA
URBANIZADA
Log da População (milhões de habitantes)
8
6.25
4.5
2.75
1
1 1.75 2.5 3.25 4
Log da Área urbanizada (Km2)

18. TRANSFORMAÇÃO PELA RAÍZ
QUADRADA

19. DISTRIBUIÇÃO DA POPULAÇÃO
POR ESTADO BRASILEIRO
Frequência
12
9
6
3
0
Até 1000 1001 a 2000 2001 a 3000 3001 a 4000 4001 a 5000 Acima de 5000
Raiz quadrada da população (milhões de habitantes)

20. POPULAÇÃO POR ÁREA
URBANIZADA
Raiz Quadrada da População (milhões de
habitantes)
7000
5250.25
3500.5
1750.75
1
1 20.75 40.5 60.25 80
Raiz Quadrada da Área urbanizada (Km2)

21. ESCOLHENDO A
TRANSFORMAÇÃO CORRETA
• A medida que você começa a entender melhor os efeitos de
diferentes transformações começará a se perguntar como
escolher a transformação adequada
• Não é simples responder esta pergunta!
• Apesar de existirem métodos estatísticos para essa escolha, a
resposta geralmente envolve tentativa e erro
• Uma estratégia geral é aplicar algumas das transformações mais
utilizadas, observar os resultados e escolher a mais adequada

22. TRANSFORMAÇÕES COMUNS
Método Operação
Matemática
Indicações Contra-indicações
Log ln(x)
log(x)
Obliquidade à
direita
Valores nulos
Valores negativos
Raiz Quadrada x Obliquidade à
direita Valores negativos
Quadrado x Obliquidade à
esquerda Valores negativos
Raíz Cúbica x
Obliquidade à
direita
Valores Negativos
Menos efetiva que
o log na
normalização
Recíproco 1/x
Diminuir valores
grandes e
aumentar valores
pequenos
Valores nulos
Valores negativos

23. ARMADILHAS
• Uma vez que os métodos de transformação envolvem a
aplicação de uma função matemática aos dados, você precisa
tomar cuidado na hora de interpretar e apresentar os
resultados por conta da mudança na unidade
• Por exemplo, ao apresentar a transformação logarítmica nos
exemplos passamos a tratar do log da população e não mais
da população.
• Isso precisa ficar bem claro nos gráficos