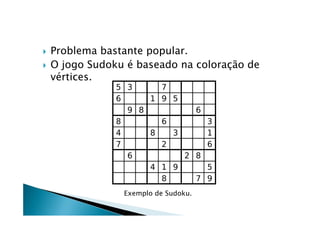
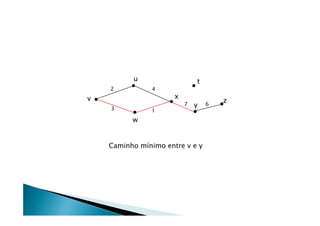
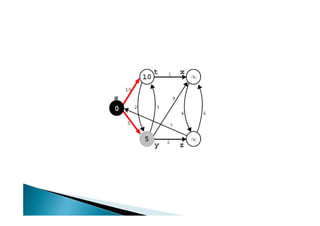
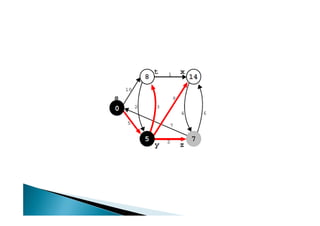
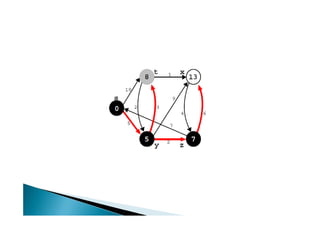
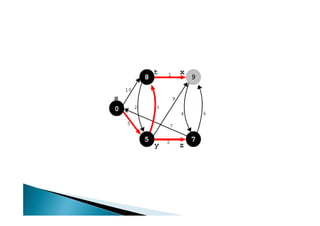
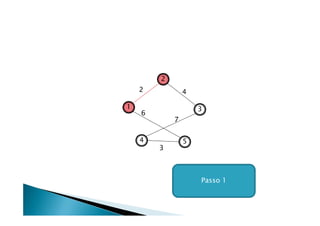
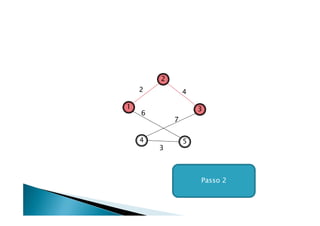
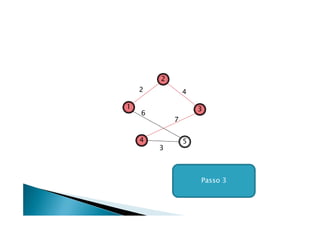
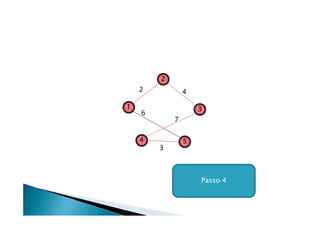
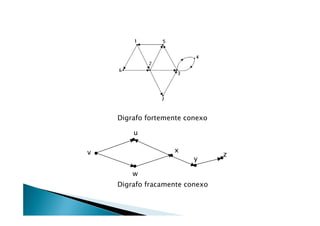
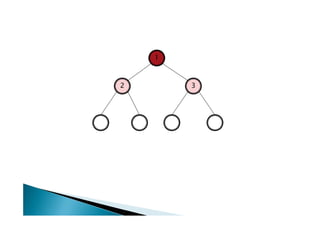
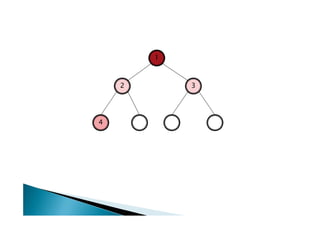
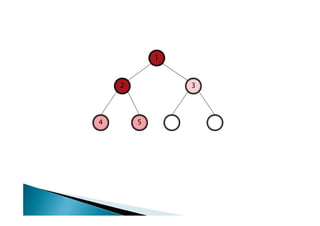
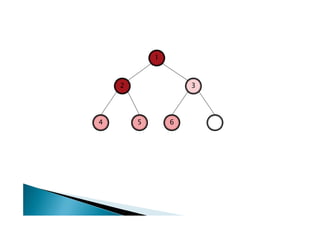
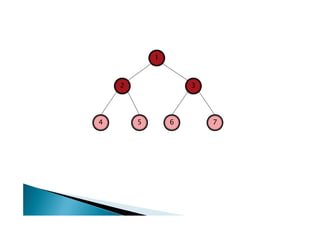
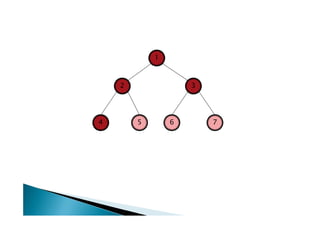
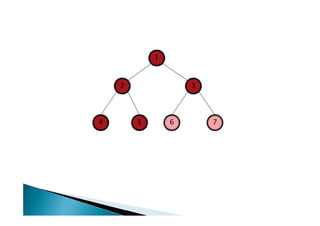
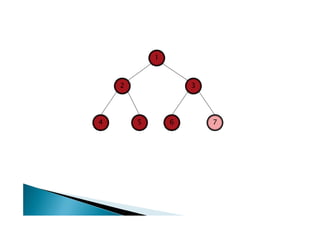
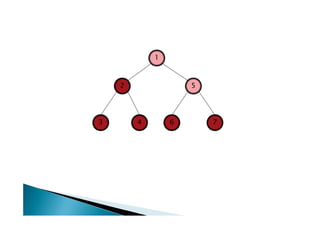
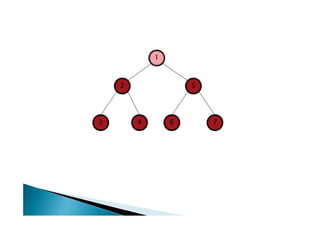
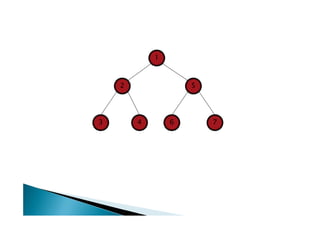
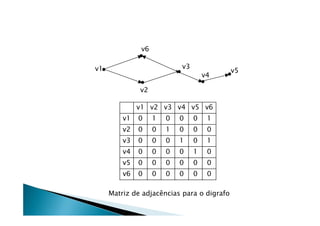
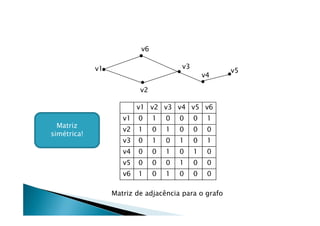
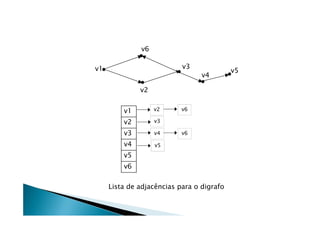
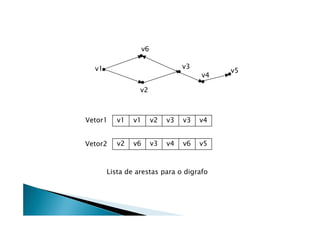
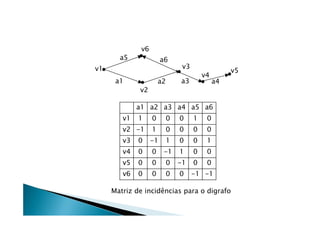
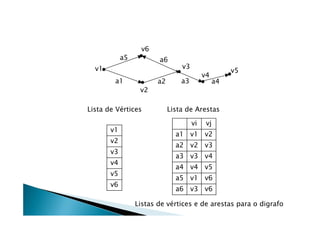
O documento discute grafos e suas propriedades. Em três frases: Discutiu os conceitos básicos de grafos incluindo vértices, arestas e graus. Apresentou exemplos de grafos simples e direcionados e discutiu representações computacionais como matriz de adjacências e lista de adjacências. Também abordou problemas clássicos em grafos como busca em largura, busca em profundidade e conectividade.

1. Bianca de Almeida Dantas

2.  Introdução
 Terminologia
 Exemplos de Grafos
 Digrafos
 Percursos em Grafos
 Representação Computacional
 Problemas em Grafos
 Conclusões
 Bibliografia

3.  Ramo da matemática que se utiliza de
modelos (os grafos) para estudar as relações
entre os objetos de um conjunto.

4. Figura 1 – Grafo com 4 vértices e 6 arestas.

5.  Diversos problemas podem ser representados
por grafos:
◦ Trajetos entre cidades
◦ Roteamento de veículos
◦ Mapa de páginas de um site
◦ Redes de computadores
◦ Representação de máquinas de estados finitos
 A obtenção de estruturas de dados e de
algoritmos eficientes para manipulação de
grafos é uma área de grande interesse da
ciência da computação.

6.  Um grafo é um par ordenado (V, A), onde V é
um conjunto qualquer e A é um subconjunto
de V(2) , o conjunto de todos os pares não-
ordenados de V. Chamamos os elementos de
V de vértices e os elementos de A de arestas.
 Considere dois vértices u e v e uma aresta
que os conecta, denotada por uv ou vu.
Dizemos que a aresta uv incide em u e em v
ou, ainda, que u e v são pontas da aresta uv.

7.  Quando dois vértices são pontas de uma
mesma aresta, eles são ditos vizinhos ou
adjacentes.
 Em algumas situações, é interessante dar
nome a um grafo, por exemplo, G. Neste
caso, o conjunto de vértices e de arestas são
denotados por V(G) e A(G), respectivamente.
 O número de vértices, |V(G)|, de G é
denotado por n e o número de arestas, |A(G)|,
é denotado por m.

8. Vértices: t, u, v, w, x, y, z
Arestas: xu, uv, vw, wx, xy, yz
n=7
m=6

9.  O grau de um vértice é definido como o
número de arestas incidentes em tal vértice.
2 0
2 3 1
2
2

10.  Um grafo regular é aquele em que todos os
vértices possuem o mesmo grau.
 Um grafo regular com vértices de grau k é
chamado de k-regular.
0-regular 1-regular 2-regular 3-regular

11.  Um grafo completo G é aquele que possui
arestas conectando todos os pares de vértices,
ou seja, G(V, V(2)). Usualmente, são nomeados
usando a letra K.
Também é um
grafo 5-regular
Grafo completo com 6 vértices (K6)

12.  O complemento de um grafo (V, A) é definido
como (V, V(2) A).
u z u z
u z
y v y
v y v
w x w x
w x
Grafo Grafo completo Complemento

13.  Um caminho entre dois vértices v1 e v2 de um
grafo é a sequência de arestas do trajeto
saindo de v1 em direção a v2. Os vértices v1 e
v2 são ditos extremos do caminho.
 O comprimento de um caminho é o seu
número de arestas.
 Um caminho que começa e termina no mesmo
vértice é chamado de ciclo ou circuito.
 Um ciclo de comprimento 1 é chamado de
laço.

14. u t
v x
z
y
w
Qual é o caminho de v a y?

15. u t
v x
z
y
w
Alternativa 1
Comprimento: 3

16. u t
v x
z
y
w
Alternativa 2
Comprimento: 3

17. Ciclo a partir do vértice u
u t
v x
z
y
w

18. u
t
v x
z
y
w
Um laço no
vértice t

19.  Em um grafo simples não existem laços e há
no máximo uma aresta entre quaisquer par
de vértices, ou seja, não existem arestas
paralelas.
 Um grafo G(V, A) é conexo se existe um
caminho entre todos os pares de vértices de
V.

20.  Grafos podem ter pesos associados a suas
arestas, representado por um número
rotulando cada aresta.
 Neste caso, o comprimento do caminho entre
dois vértices (ou peso do caminho)
corresponde à soma dos pesos das arestas
que compõem o caminho.

21. Dizemos que o caminho vermelho é um caminho
mínimo entre v e y, pois tem o menor peso entre
os caminhos possíveis.
u t
2 4
v x
z
3
7 y 6
1
w
Caminhos entre v e y?
Alternativa 1 (verde):Peso = 13
Alternativa 2 (vermelho):Peso = 11

22.  O grafo dos estados do Brasil é definido
assim: cada vértice é um dos estados da
República Federativa do Brasil; dois estados
são adjacentes se têm uma fronteira comum.

23. Grafo que representa as adjacências entre os estados do Brasil

24.  Tipos especiais de grafos nos quais todas as
arestas são direcionadas.
 Caminhos em digrafos devem levar em
consideração a direção das arestas.
 Dois tipos de graus de vértices:
◦ Grau de entrada: número de arestas que “chegam”
no vértice;
◦ Grau de saída: números de arestas que “saem” do
vértice.

25. u t
v x
z
y
w
Caminho de v até y? E de y até
v?

26. Quais os graus
de entrada (E) e
saída (S)?
E: 0
E: 2 S: 0
u t
S: 0
v x
z
y
E: 0 E: 1 E: 1
S: 2 w S: 2 E: 1 S: 0
E: 1 S: 1
S: 1
Única alternativa de v até y!
De y até v não existe
caminho.

27.  Um digrafo D(V, A) é dito fortemente conexo
se, para todos os pares de vértices (u, v)
existe caminho de u para v e de v para u.
 Um digrafo é fracamente conexo se sua
“versão não-direcionada” for conexa.

28. Digrafo fortemente conexo
u
v x
z
y
w
Digrafo fracamente conexo

29.  Existem duas formas de percorrer todos os
vértices de um grafo, geralmente chamadas
de buscas:
◦ Busca em Largura ou BFS (Breadth-First Search);
◦ Busca em Profundidades ou DFS (Depth-First
Search).

30.  Nesse percurso, partimos de um vértice
inicial e percorremos todos os seus vizinhos,
um a um, e então percorremos os vizinhos de
cada um de seus vizinhos, na ordem em que
foram visitados no passo anterior.

32. 1

33. 1
2

34. 1
2 3

35. 1
2 3
4

36. 1
2 3
4 5

37. 1
2 3
4 5 6

38. 1
2 3
4 5 6 7

39. 1
2 3
4 5 6 7

40. 1
2 3
4 5 6 7

41. 1
2 3
4 5 6 7

42. 1
2 3
4 5 6 7
Grafos com essa estrutura
são chamados de árvores.

43.  Partindo de um vértice inicial, esse algoritmo
visita os vértices um a um até o “filho mais
profundo” que pode ser alcançado e, após
descer na hierarquia, passa para o próximo
“filho”.

44. 1

45. 1
2

46. 1
2
3

47. 1
2
3

48. 1
2
3 4

49. 1
2
3 4

50. 1
2
3 4

51. 1
2 5
3 4

52. 1
2 5
3 4 6

53. 1
2 5
3 4 6

54. 1
2 5
3 4 6 7

55. 1
2 5
3 4 6 7

56. 1
2 5
3 4 6 7

57. 1
2 5
3 4 6 7

58.  Existem diversas estruturas que podem ser
utilizadas para armazenar as informações de
um grafo ou digrafo. Pode-se citar:
◦ Matriz de adjacências;
◦ Lista de adjacências;
◦ Lista de arestas;
◦ Matriz de incidências;
◦ Listas de vértices e arestas

59.  A matriz de adjacências para um grafo
(digrafo) G (V, A) é uma matriz M de
dimensão |V|x|V| na qual o elemento Mi,j será
igual a 1 se existe uma aresta de i para j ou
0, caso contrário.

60. v6
v1 v3
v5
v4
v2
v1 v2 v3 v4 v5 v6
v1 0 1 0 0 0 1
v2 0 0 1 0 0 0
v3 0 0 0 1 0 1
v4 0 0 0 0 1 0
v5 0 0 0 0 0 0
v6 0 0 0 0 0 0
Matriz de adjacências para o digrafo

61. v6
v1 v3
v5
v4
v2
v1 v2 v3 v4 v5 v6
v1 0 1 0 0 0 1
Matriz
v2 1 0 1 0 0 0
simétrica!
v3 0 1 0 1 0 1
v4 0 0 1 0 1 0
v5 0 0 0 1 0 0
v6 1 0 1 0 0 0
Matriz de adjacência para o grafo

62.  Uma lista de adjacências para um grafo
(digrafo) G (V, A) armazena para cada vértice
u de V uma lista de todos os vértices v para
os quais existe uma aresta uv.

63. v6
v1 v3
v5
v4
v2
v1 v2 v6
v2 v3
v3 v4 v6
v4 v5
v5
v6
Lista de adjacências para o digrafo

64.  A representação de um grafo (digrafo) G(V,A)
por lista de arestas utiliza dois vetores com
|A| elementos para armazenar os extremos
das arestas pertencentes a A.

65. v6
v1 v3
v5
v4
v2
Vetor1 v1 v1 v2 v3 v3 v4
Vetor2 v2 v6 v3 v4 v6 v5
Lista de arestas para o digrafo

66.  Uma matriz de incidências para um digrafo
G(V,A) é uma matriz M de dimensão |V|x|A|
em que cada elemento segue a equação:
 1, se v i for o vértice inicial de a j

mij   1, se v i for o vértice final de a j

 0, caso contrário
 No caso de grafos não-direcionais, temos
que mij será 1 se vi for extremo de aj ou 0
caso contrário.

67. v6
a5 a6
v1 v3
v5
v4
a1 a2 a3 a4
v2
a1 a2 a3 a4 a5 a6
v1 1 0 0 0 1 0
v2 -1 1 0 0 0 0
v3 0 -1 1 0 0 1
v4 0 0 -1 1 0 0
v5 0 0 0 -1 0 0
v6 0 0 0 0 -1 -1
Matriz de incidências para o digrafo

68.  As listas de vértices e de arestas são a forma
mais simples de representação de um grafo
(digrafo) G(V,A). São mantidas duas listas
uma com todos os vértices de G e outra com
todas as arestas e seus extremos.

69. v6
a5 a6
v1 v3
v5
v4
a1 a2 a3 a4
v2
Lista de Vértices Lista de Arestas
vi vj
v1
a1 v1 v2
v2
a2 v2 v3
v3
a3 v3 v4
v4
a4 v4 v5
v5
a5 v1 v6
v6
a6 v3 v6
Listas de vértices e de arestas para o digrafo

70.  Fecho transitivo
 Problema do caminho mínimo
 Caixeiro viajante
 Carteiro chinês
 Coloração de vértices

71.  O fecho transitivo Dt de um digrafo D é
obtido adicionando uma aresta dirigida entre
todos os pares de vértices vi e vj entre os
quais exista um caminho que saia de vi em
direção a vj.
Digrafo Dt de D

72.  Ou seja, o fecho transitivo representa a
inserção de uma nova aresta entre os vértices
conectados indiretamente por um caminho.
 Diversos algoritmos foram propostos para
solução.
 Muitas soluções se baseiam na matriz de
adjacências.

73. 1 2 3 4 5
1 2 1 0 0 1 0 0
2 0 0 1 1 0
3 4 3 0 0 0 0 1
4 0 0 0 0 1
5
5 0 0 0 0 0

74. 1 2 3 4 5
1 2 1 0 0 1 0 1
2 0 0 1 1 1
3 4 3 0 0 0 0 1
4 0 0 0 0 1
5
5 0 0 0 0 0

75.  Complexidade θ(n3)
 Baseia-se na premissa de que, se existe uma
aresta de vi para vk e uma aresta de vk para vj,
então, deve existir uma aresta de vi para vj.
 Sua estrutura permite fácil paralelização.

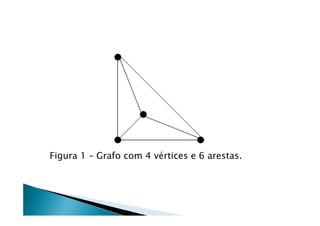
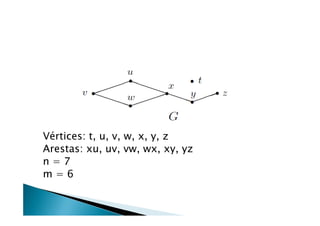
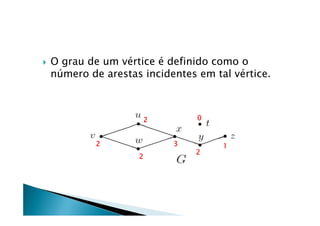
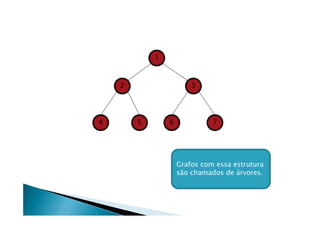
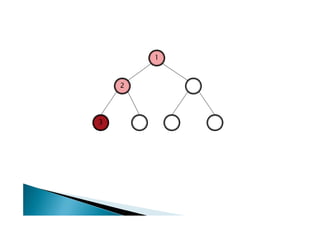
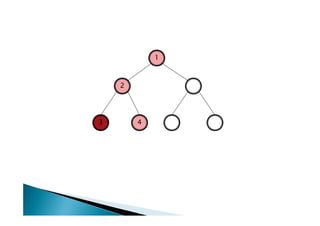
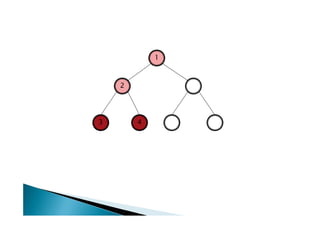
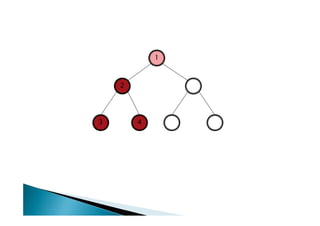
76. Algoritmo
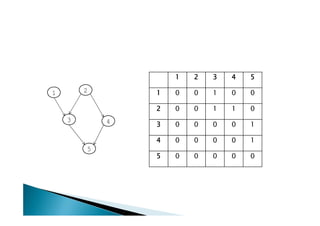
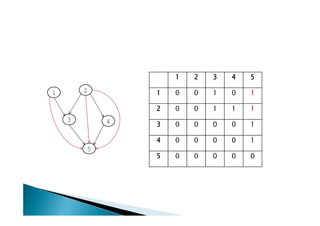
Entrada: M – matriz de adjacências
Saída: Mt – matriz de adjacências do
fecho
inicio
n <- |V|
Mt <- M
para k de 1 ate n faca
para i de 1 ate n faca
para j de 1 ate n faca
se Mt[i,k]=1 e Mt[k,j]=1 entao
Mt[i,j] <- 1
fimse
fimpara
fimpara
fimpara
fimalgoritmo

77.  O problema do caminho mínimo consiste na
minimização do custo de travessia de
um grafo entre dois ou mais vértices, levando
em consideração o peso de cada aresta
percorrida.
 Caso os pesos sejam omitidos, considere-os
iguais a um.

78. u t
2 4
v x
z
3
7 y 6
1
w
Caminho mínimo entre v e y

79.  Computa os caminhos mínimos a partir de
um vértice inicial v a todos os demais
vértices.
 Ele utiliza uma estratégia gulosa baseada na
busca em largura.
 Funciona apenas para grafos com pesos
positivos.

88.  Bellman-Ford: permite que as arestas tenham
peso negativo.
 A*: heurística que também permite arestas
negativas.
 Floyd-Warshall: distância entre todos os
pares de vértices do grafo.
 Johnson: realiza a mesma tarefa do anterior,
podendo ser mais eficiente em grafos
esparsos.

89.  Conhecido pela sigla TSP (Travelling Salesman
Problem), consiste em encontrar o menor
circuito a partir de um vértice fonte v e que
passe por todos os demais vértices
exatamente uma vez.
 Também é um problema de otimização .

90. 2
2 4
1 3
3
6
7
3
3
4 5
3
Qual rota o caixeiro
deve seguir a partir
de 1?

91. 2
2 4
1 3
3
6
7
3
3
4 5
3
Passo 1

92. 2
2 4
1 3
3
6
7
3
3
4 5
3
Passo 2

93. 2
2 4
1 3
3
6
7
3
3
4 5
3
Passo 3

94. 2
2 4
1 3
3
6
7
3
3
4 5
3
Passo 4

95. . Essa é a única
solução????
2
2 4
1 3
3
6
7
3
3
4 5
3
Fim

96.  Achar a melhor solução é um problema
bastante difícil, envolvendo a exploração de
todas as possibilidades.
 Problema NP-completo!
 A complexidade do problema cresce de
acordo com o tamanho do gráfico.
 Utiliza heurísticas para encontrar uma
aproximação para o problema, por exemplo,
colônia de formigas.

97.  O problema do carteiro chinês, ou problema
da inspeção de rotas, consiste em encontrar
um ciclo em um grafo conexo e não
direcionado que passe por todas as suas
arestas exatamente uma única vez.

98. 2
2 4
1 3
6
7
4 5
3
Qual rota o carteiro
deve seguir a partir
de 1?

99. 2
2 4
1 3
6
7
4 5
3
Passo 1

100. 2
2 4
1 3
6
7
4 5
3
Passo 2

101. 2
2 4
1 3
6
7
4 5
3
Passo 3

102. 2
2 4
1 3
6
7
4 5
3
Passo 4

103. Novamente um problema difícil
de otimizar.
2
2 4
1 3
6
7
4 5
3
Final.

104.  O problema da coloração de grafos consiste
em rotular componentes do grafo (vértices,
arestas ou faces) com uma determinada cor
de forma que não haja dois elementos
adjacentes da mesma cor.
 No caso de vértices, dois vértices vizinhos
precisam ser coloridos de cores diferentes.

105.  No caso de vértices, dois vértices vizinhos
precisam ser coloridos de cores diferentes.
Coloração de vértices.

106.  No caso de arestas, arestas adjacentes ao
mesmo vértice devem ter cores diferentes.
Coloração de arestas.

107.  No caso de faces, as faces que compartilham
fronteiras não devem ter a mesma cor.
Coloração de faces.

108.  Problema bastante popular.
 O jogo Sudoku é baseado na coloração de
vértices.
Exemplo de Sudoku.

109.  Problemas em grafos podem:
◦ Ser bastante custosos para resolver;
◦ Demandar capacidade de processamento elevada;
◦ Exigir grande quantidade de espaço de
armazenamento.
 Busca por alternativas à computação
sequencial tradicional.
 Desenvolvimento de novas heurísticas e
utilização de múltiplos núcleos de
processamento.

110.  Cáceres, E.N.; Song, S.W.; Szwarcfiter, J.L. A
Parallel Algorithm for Transitive Closure.
 Cormen. Thomas (2000); Leiserson, Charles.;
Rivest, Ronald. Introduction to Algorithms,
McGraw-Hill.
 http://www.ime.usp.br/~pf/teoriadosgrafos/
 http://professor.ufabc.edu.br/~leticia.bueno/cla
sses/teoriagrafos/materiais/caminhominimo.pdf
 http://www.prp.unicamp.br/pibic/congressos/xv
icongresso/paineis/043171.pdf
 http://www.icmc.sc.usp.br/~sandra/2/cor.htm
 http://pt.wikipedia.org