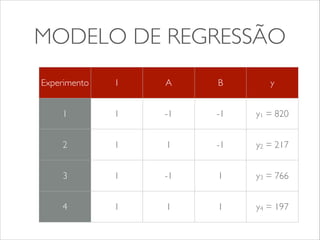
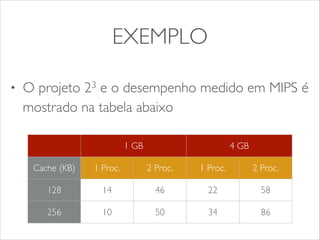
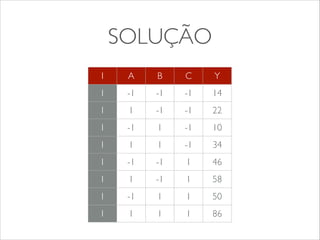
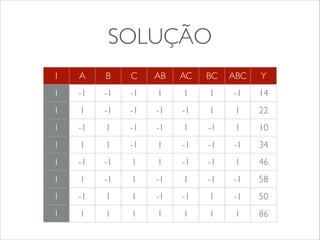
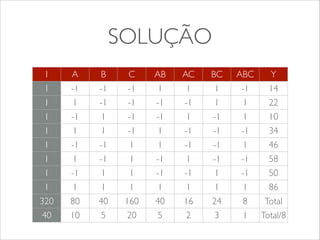
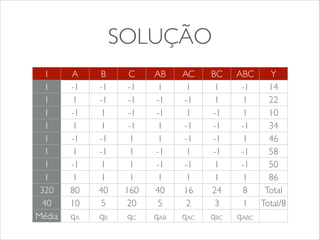
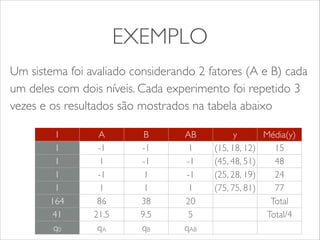
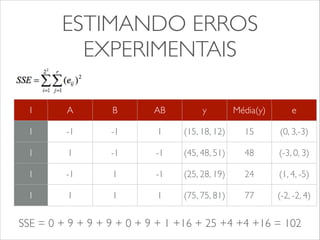
O documento apresenta os conceitos e tipos de projetos de experimentos, descrevendo como eles podem ser usados para comparar sistemas e algoritmos de forma quantitativa. Explica termos como fatores, níveis e replicação. Detalha os objetivos de um projeto de experimento e como ele pode ser usado para obter informações sobre o objeto de estudo com menor esforço. Apresenta exemplos de projetos fatoriais 22 e 23 para ilustrar a construção e análise de experimentos.

1. PROJETO DE EXPERIMENTOS
Alexandre Duarte - http://alexandre.ci.ufpb.br/ensino/iad

2. OBJETIVOS
• Apresentar a terminologia básica de um projeto
de experimento
• Descrever o processo de elaboração de um
projeto de experimentos
• Apresentar os tipos mais comuns de projetos de
experimento

3. PRA QUE SERVE UM PROJETO
DE EXPERIMENTO?
• Comparar quantitativamente
• Sistemas
• Algoritmos
• Protótipos
• Modelos
• etc

4. TERMINOLOGIA
• Replicação: significa (re-)executar o experimento
com uma configuração específica de níveis para cada
um dos fatores
• Ajuda a identificar o impacto de erros
experimentais
• Interação: ocorre quando o efeito de um fator
depende do nível de um outro fator

5. TERMINOLOGIA
• Variável resposta: o que se desejar medir
• Fatores: variáveis de entrada do experimento
• O que pode ser controlado pelo experimentador
• Níveis: valores específicos que podem ser atribuídos a
cada fator
• Contínuos, discretos ou categóricos

6. PERGUNTAS BÁSICAS
• Você conhece as métricas?
• Você conhece os fatores?
• Você conhece os níveis?

7. VOCÊ SABE COMO PROJETAR UM
EXPERIMENTO QUE COMPROVE OU
REFUTE AS SUAS HIPÓTESES DE
PESQUISA?

8. OBJETIVOS DE UM PROJETO
DE EXPERIMENTO
• Obter a maior quantidade possível de informação sobre o objeto em
estudo
• Reduzir o trabalho/esforço de experimentação
• Tipicamente significa rodar o menor número de experimentos
possível
• Realizar mais experimentos não é bom (gasta-se tempo e recursos)
principalmente se for você o responsável por realizá-lo
• Facilitar a análise dos dados coletados

9. REPLICAÇÕES EXPERIMENTAIS
• O objeto em estudo será avaliado utilizando vários
níveis de diferentes fatores
• Um execução com uma configuração particular de
níveis recebe o nome de replicação
• Em geral, é necessário executar uma mesma replicarão
várias vezes para permitir a validação e verificação
estatística dos resultados

10. INTERAÇÃO ENTRE FATORES
• Alguns fatores têm efeitos completamente independentes um do
outro
• Exemplo: Duplique o nível de um fator e reduzirá o valor da
variável resposta à metade, independente dos demais fatores
• Mas os efeitos de alguns fatores dependem de outros fatores
• Fatores inter-atuantes
• A presença de fatores inter-atuantes complica o projeto experimental

11. ERROS COMUNS
• Ignorar o erro experimental
• Existência de parâmetros não controlados (não são fatores)
• Não isolamento dos efeitos de diferentes fatores
• Ignorar as interações entre os fatores
• Projetos que requerem um número excessivo de experimentos
• O que é um número excessivo ?

12. TIPOS DE PROJETOS DE
EXPERIMENTO
• Projeto simples
• Projeto fatorial completo
• Projeto fatorial fracionado

13. PROJETO SIMPLES
• Varie um fator de cada vez
• Assume que os fatores não interagem
• Usualmente requer mais esforço do que se pensa
• Tente evitar este tipo de projeto

14. PROJETO FATORIAL
COMPLETO
• Testa todas as combinações possíveis para os níveis dos
fatores
• Captura informação completa sobre a interação entre os
fatores
• É, no entanto, um trabalho enorme!!!
• Principalmente quando envolve fatores com muitos
níveis diferentes.

15. REDUZINDO O TRABALHO COM
UM PROJETO FATORIAL COMPLETO
• Reduza o número de níveis por fator
• Geralmente é uma boa opção
• Especialmente quando se sabe quais são os fatores mais importantes
• Usar mais níveis para fatores mais relevantes
• Reduza o número de fatores
• Simplifica o modelo experimental
• Cuidado para não remover fatores importantes

16. PROJETO FATORIAL
FRACIONADO
• Mede apenas uma combinação de níveis de fatores
• O projeto precisa ser cuidadosamente planejado para
capturar melhor qualquer interação que possa existir
• Menos trabalho porém pode apresentar maior imprecisão
• Muito útil quando se sabe a priori que alguns fatores não
interagem

17. PROJETO FATORIAL 2K
• Usado para determinar os efeitos de K fatores com 2 níveis
cada
• Em geral, este tipo de projeto é utilizado de maneira preliminar,
antes de um estudo mais detalhado
• Cada fator é representado por seus níveis máximo e mínimo
• Pode oferecer “insights" sobre as interações entre os vários
fatores

18. EFEITOS UNIDIRECIONAIS
• Efeitos que variam em uma única direção a medida
que variamos o nível de um fator
• Se essa característica é conhecia a priori, um projeto
fatorai 2k nos níveis máximo e mínimo pode ser ainda
mais útil
• Pode demonstrar claramente quando um fator tem
efeito significativo no experimento

19. PROJETO FATORIAL 22
• Dois fatores com dois níveis cada um
• Tipo mais simples de projeto de experimento
fatorial
• Exemplo para ilustrar a construção de um
experimento 2k

20. EXEMPLO
• Queremos avaliar o desempenho de uma máquina
de busca composta por N servidores;
• Podemos utilizar vários algoritmos de
escalonamento para distribuir as consultas
• O objetivo é completar as consultas no menor
tempo possível

21. FATORES E NÍVEIS
• Primeiro fator: número de núcleos de processamento
• Varia entre 8 e 64
• Segundo fator: algoritmos de escalonamento
• Varia entre aleatório e round-robin
• Outros fatores existem mas serão ignorados neste
exemplo

22. DEFININDO AS VARIÁVEIS
XA = -1 se 8 servidores
1 se 64 servidores
XB = -1 se escalonamento aleatório
1 se round-robin

23. DADOS AMOSTRAIS
• Execução única de uma mesma carga de consultas
nas duas configurações resultado nos seguintes
tempos de execução
8 serv. (-1) 64 serv. (1)
Aleatório (-1) 820 217
Round Robin
(1) 776 197

24. MODELO DE REGRESSÃO
Experimento I A B y
1 1 -1 -1 y1 = 820
2 1 1 -1 y2 = 217
3 1 -1 1 y3 = 766
4 1 1 1 y4 = 197

25. MODELO DE REGRESSÃO
• y = q0 + qAxA + qBxB + qABxAxB
• 820 = q0 - qA - qB + qAB
• 217 = q0 + qA - qB - qAB
• 776 = q0 - qA + qB - qAB
• 197 = q0 + qA + qB + qAB

26. SOLUCIONANDO PARA OS
QI'S
• q0 = (y1 + y2 + y3 + y4) / 4
• qA = (-y1 + y2 - y3 + y4) / 4
• qB = (-y1 - y2 + y3 + y4) / 4
• qAB = (y1 - y2 - y3 + y4) / 4

27. SOLUÇÃO DAS EQUAÇÕES
• q0 = (820 + 217 + 776 + 197) / 4 = 502.5
• qA = (-820 + 217 - 776 + 197) / 4 = -295.5
• qB = (-820 - 217 + 776 + 197) / 4 = -16
• qAB = (820 - 217 - 776 + 197) / 4
• Assim, y = 502.5 - 295.5xA - 16xB + 6xAxB

28. SOLUÇÃO DAS EQUAÇÕES
• y = 502.5 - 295.5xA - 16xB + 6xAxB
• O número de servidores (A) tem maior impacto
no tempo de resposta, e faz uma diferença de
+-295.5

29. CALCULANDO A VARIAÇÃO
• Calcule a variância amostral de y
• Numerador é o SST (variação total)
• Outra fórmula, SST = 22qA2 + 22qB2 + 22qAB2
• Podemos utilizar isso para entender as causas da
variação

30. TERMOS NO SST
• 22qA2 é parte da variação explicada pelo efeito de
A (SSA)
• 22qB2 é parte da variação explicada pelo efeito de
B (SSB)
• 22qAB2 é parte da variação explicada pelo efeito da
interação de A e B (SSAB)

31. CALCULANDO A VARIAÇÃO
• SSA = 349281
• SSB = 1024
• SSAB = 144
• SST = 350449
• Podemos agora calcular a fração da variação total devida
a cata fator

32. FRAÇÕES DA VARIAÇÃO
• Fração explicada por A: 99.67%
• Fração explicada por B: 0.29%
• Fração explica pela interação entre A e B: 0.04%
• Quase toda a variação no resultado é consequência
do número de servidores. O escalonamento tem um
efeito desprezível na performance do sistema.

33. PROJETO FATORIAL 2K
• Usado para analisar os efeitos de k fatores, cada
um com 2 níveis
• Projetos 22 são um caso especial

34. EXEMPLO
• No projeto de um sistema, os três fatores de
maior impacto e que precisam ser estudados são :
tamanho do cache, tamanho da memória, e se 1
ou 2 processadores serão usados.
Fator Nível -1 Nível I
A: Tamanho da memória 1 GB 4 GB
B: Tamanho do Cache 128 KB 256 KB
C: # Processadores 1 2

35. EXEMPLO
• O projeto 23 e o desempenho medido em MIPS é
mostrado na tabela abaixo
1 GB 4 GB
Cache (KB) 1 Proc. 2 Proc. 1 Proc. 2 Proc.
128 14 46 22 58
256 10 50 34 86

36. SOLUÇÃO
I A B C Y
1 -1 -1 -1 14
1 1 -1 -1 22
1 -1 1 -1 10
1 1 1 -1 34
1 -1 -1 1 46
1 1 -1 1 58
1 -1 1 1 50
1 1 1 1 86

37. SOLUÇÃO
I A B C AB AC BC ABC Y
1 -1 -1 -1 1 1 1 -1 14
1 1 -1 -1 -1 -1 1 1 22
1 -1 1 -1 -1 1 -1 1 10
1 1 1 -1 1 -1 -1 -1 34
1 -1 -1 1 1 -1 -1 1 46
1 1 -1 1 -1 1 -1 -1 58
1 -1 1 1 -1 -1 1 -1 50
1 1 1 1 1 1 1 1 86

38. SOLUÇÃO
I A B C AB AC BC ABC Y
1 -1 -1 -1 1 1 1 -1 14
1 1 -1 -1 -1 -1 1 1 22
1 -1 1 -1 -1 1 -1 1 10
1 1 1 -1 1 -1 -1 -1 34
1 -1 -1 1 1 -1 -1 1 46
1 1 -1 1 -1 1 -1 -1 58
1 -1 1 1 -1 -1 1 -1 50
1 1 1 1 1 1 1 1 86
320 80 40 160 40 16 24 8 Total
40 10 5 20 5 2 3 1 Total/8

39. SOLUÇÃO
I A B C AB AC BC ABC Y
1 -1 -1 -1 1 1 1 -1 14
1 1 -1 -1 -1 -1 1 1 22
1 -1 1 -1 -1 1 -1 1 10
1 1 1 -1 1 -1 -1 -1 34
1 -1 -1 1 1 -1 -1 1 46
1 1 -1 1 -1 1 -1 -1 58
1 -1 1 1 -1 -1 1 -1 50
1 1 1 1 1 1 1 1 86
320 80 40 160 40 16 24 8 Total
40 10 5 20 5 2 3 1 Total/8
Média qA qB qC qAB qAC qBC qABC

40. SOLUÇÃO
40 10 5 20 5 2 3 1 Total/8
Média qA qB qC qAB qAC qBC qABC
SST = 23 (qA2+qB2+qC2+qAB2+qAC2+qBC2+qABC2)
SST = 8(102+52+202+52+22+32+12)
SST = 800 + 200 + 3200 + 200 +32 + 72 + 8 = 4512

41. SOLUÇÃO
• A porção de variação explicada por cada fator e suas internações são:
• A: 800/4512 = 18%
• B: 200/4512 = 4%
• C: 3200/4512 = 71%
• AB: 200/4512 = 4%
• AC: 32/4512 = 1%
• BC: 72/4512 = 2%
• ABC: 8/4515 = 0% (pode ser ignorado)

42. PROJETOS FATORIAIS 2KR
• Projetos fatoriais 2k não permitem estimar os erros
experimentais já que nenhum experimento é repetido
• Se cada um dos 2k experimentos forem repetidos r vezes,
teremos 2kr observações
• Poderemos estimar erros experimentais
• Nos permite calcular o % da variação devido aos erros
experimentais

43. PROJETOS FATORIAIS 22R
• Assume o modelo genérico:
• y = q0 + qAxA + qBxB + qABxAxB + e
• Computar os efeitos (coeficientes) de forma similar
aos projetos 2k

44. EXEMPLO
Um sistema foi avaliado considerando 2 fatores (A e B) cada
um deles com dois níveis. Cada experimento foi repetido 3
vezes e os resultados são mostrados na tabela abaixo
I A B AB y Média(y)
1 -1 -1 1 (15, 18, 12) 15
1 1 -1 -1 (45, 48, 51) 48
1 -1 1 -1 (25, 28, 19) 24
1 1 1 1 (75, 75, 81) 77
164 86 38 20 Total
41 21.5 9.5 5 Total/4
q0 qA qB qAB

45. ESTIMANDO ERROS
EXPERIMENTAIS
I A B AB y Média(y) e
1 -1 -1 1 (15, 18, 12) 15 (0, 3,-3)
1 1 -1 -1 (45, 48, 51) 48 (-3, 0, 3)
1 -1 1 -1 (25, 28, 19) 24 (1, 4, -5)
1 1 1 1 (75, 75, 81) 77 (-2, -2, 4)
SSE = 0 + 9 + 9 + 9 + 0 + 9 + 1 +16 + 25 +4 +4 +16 = 102

46. EXPLICANDO A VARIAÇÃO
• SST = SSA + SSB + SSAB + SSE
• SSA = 22rqA2
• SSB = 22rqB2
• SSAB = 22rqAB2

47. EXPLICANDO A VARIAÇÃO
• SSA = 22rqA2 = 4*3*(21.5)2 = 5547
• SSB = 22rqB2 = 4*4*(9.5)2 = 1083
• SSAB = 22rqAB2 = 4*3*(5)2 = 300
• SST =5547 + 1083 + 300 + 102 = 7032

48. EXPLICANDO A VARIAÇÃO
• O fator A explica 5547/7032 = 78.9% da variação
• O fator B explica 1083/7032 = 15.4%
• A interação entre A e B explica 300/7032 = 4.3%
• Os demais 1.4% são inexplicados e atribuídos a
erros experimentais