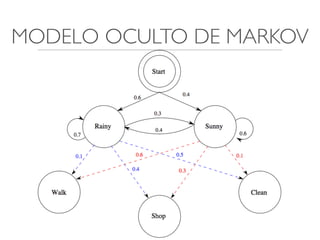
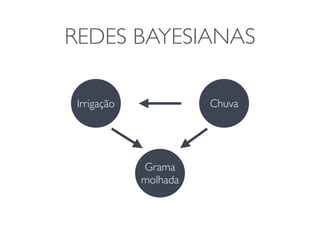
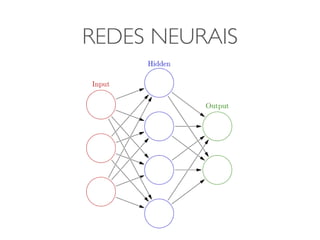
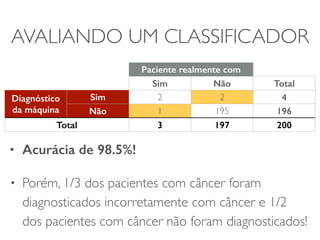
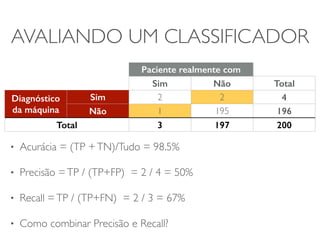
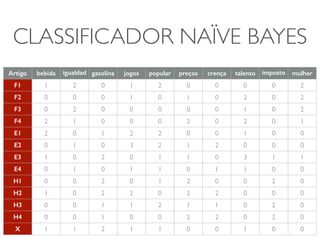
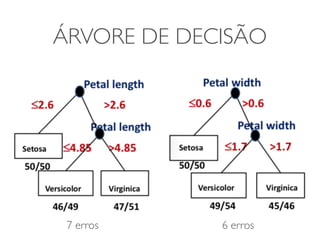
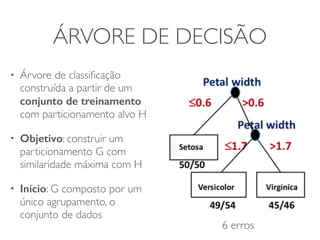
O documento discute diferentes estruturas de correlação e classificadores, incluindo: 1) Modelos ocultos de Markov, redes bayesianas e redes neurais como formas de encontrar regras para prever uma variável alvo a partir de variáveis de entrada. 2) O classificador Naive Bayes, que usa a probabilidade condicional de características dados os rótulos de classe para fazer predições de classe. 3) Árvores de decisão, que constroem particionamentos recursivos dos dados para predição de classe.

1. CORRELAÇÃO E CLASSIFICAÇÃO
Alexandre Duarte - http://alexandre.ci.ufpb.br/ensino/iad

2. AGENDA
• Estruturas de correlação
• Classificador Naive Bayes
• Árvores de Decisão
• Avaliando um Classificador

3. ESTRUTURAS DE CORRELAÇÃO
• Tipicamente, dividimos as variáveis em duas partes para podermos analisar
de diferentes formas os relacionamentos entre elas
• Variável de entrada: X
• Variável alvo: U
• Procuramos encontrar uma regra F para estabelecer uma relação entre a
variável de entrada e a variável alvo
• U = F(X)
• Isto nos permitiria prever U a partir de X.

4. ESTRUTURAS DE CORRELAÇÃO
• A regra U=F(X) pode ser utilizada para prever U a
partir de X
• Devido a sua grande importância prática, este
problema tem recebido grande atenção de
pesquisadores
• O resultado são várias formas diferentes para
encontrar estas regras

5. MODELO OCULTO DE MARKOV
• Considere dois amigos (Alice e Bob) que moram distantes um do outro e
que se falam diariamente ao telefone sobre o que fizeram durante o dia
• Bob só se interessa por três tipos de atividade: caminhadas, compras e
limpeza do apartamento
• A escolha sobre o que fazer é determinada exclusivamente pelo clima do dia
• Alice não tem dados específicos sobre o clima da cidade onde Bob mora, mas
tem uma noção sobre a tendência de chuva ou de sol.
• Baseado no que Bob diz que fez, Alice ela tenta adivinhar como estava o clima
na cidade de Bob

6. MODELO OCULTO DE MARKOV

7. MODELO OCULTO DE MARKOV
• Usa estados observáveis para prever estados não-observáveis
• As transições entre os estados não observáveis
seguem um processo de Cadeia de Markov
• Propriedade: Os estados anteriores são irrelevantes
para a predição dos estados seguintes, desde que o
estado atual seja conhecido

8. REDES BAYESIANAS
• Uma rede bayesiana é um modelo probabilístico que representa um conjunto de
variáveis aleatórias e as dependências condicionais entre elas através de um grafo
acíclico dirigido (DAG).
• Os nós representam as variáveis aleatórias no sentido Bayesiano (quantidades
observáveis, parâmetros desconhecidos ou hipóteses)
• Os vértices representam dependências condicionais, nós não conectados
representam variáveis condicionalmente independentes umas das outras
• Por exemplo, uma rede bayesiana pode ser utilizada para representar os
relacionamentos entre sintomas e doenças.
• Dado um conjunto de sintomas, a rede poderia ser utilizada para calcular a
probabilidade da presença de diferentes doenças

9. REDES BAYESIANAS
Irrigação Chuva
Grama
molhada

10. REDES NEURAIS
• Modelos computacionais inspirados pelo sistema nervoso central
• Atualmente têm evoluído para uma abordagem mais prática, baseada
em estatística e processamento de sinais
• Utilizados para estimar ou aproximar funções que dependem de um
grande número de entradas que são geralmente desconhecidas
• Representadas por neurônios, capazes de computar valores a partir de
entradas e conexões (sinapses) entre estes neurônios
• Muito utilizadas para reconhecimento de padrões

11. REDES NEURAIS

12. ÁRVORES DE DECISÃO
• Uma árvore
mostrando a chance
de sobrevivência
dos passageiros do
Titanic
• Folhas representam
as probabilidades

13. ESTRUTURAS DE CORRELAÇÃO
• Entre as diferentes formas para as regras U = F(X),
destacam-se
• Modelo Oculto de Markov (Hidden Markov Model)
• Redes Bayesianas
• Redes Neurais
• Árvores de Decisão

14. CLASSIFICADOR NAÏVE BAYES
Artigo bebida igualdad
e
gasolina jogos popular preços crença talento imposto
s
mulher
F1 1 2 0 1 2 0 0 0 0 2
F2 0 0 0 1 0 1 0 2 0 2
F3 0 2 0 0 0 0 0 1 0 2
F4 2 1 0 0 0 2 0 2 0 1
E1 2 0 1 2 2 0 0 1 0 0
E2 0 1 0 3 2 1 2 0 0 0
E3 1 0 2 0 1 1 0 3 1 1
E4 0 1 0 1 1 0 1 1 0 0
H1 0 0 2 0 1 2 0 0 2 0
H2 1 0 2 2 0 2 2 0 0 0
H3 0 0 1 1 2 1 1 0 2 0
H4 0 0 1 0 0 2 2 0 2 0
X 1 1 2 1 1 0 0 1 0 0

15. CLASSIFICADOR NAÏVE BAYES
• Pensamento Bayesiano: considere a situação
anterior, de acordo com os 12 artigos
• Três classes F, E, e H, com probabilidades p(F) =
1/3, p(E) = 1/3 e p(H) = 1/3
• Cada classe é responsável por 4 dos 12 itens

16. CLASSIFICADOR NAÏVE BAYES
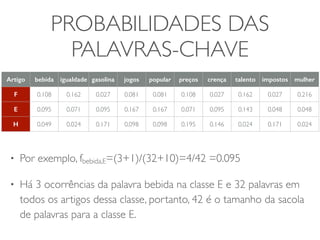
• p(F) = 1/3, p(E) = 1/3 e p(H) = 1/3
• Assuma que podemos derivar as probabilidades para o artigo x pertencer a
cada uma dessas classes [p(x|F), p(x|E), p(x|H)] a partir dos dados da tabela
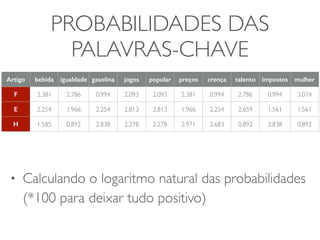
• Sendo assim, as probabilidades posteriores das classes seriam proporcionais
aos produtos (Teorema de Bayes):
• p(F|x) = p(x|F)p(F)
• p(E|x) = p(x|E)p(E)
• p(H|x)=p(x|H)p(H)

17. CLASSIFICADOR NAÏVE BAYES
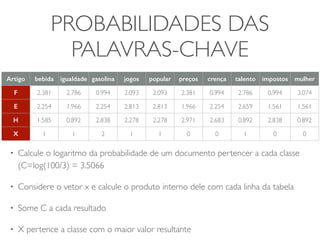
• x pertence a classe com a maior probabilidade a posterior
• p(F|x) = p(x|F)p(F)
• p(E|x) = p(x|E)p(E)
• p(H|x)=p(x|H)p(H)
• Problema: Como derivar as probabilidades de x pertencer a
cada uma das categorias [p(x|F), p(x|E), p(x|H)] a partir da tabela
?

18. CLASSIFICADOR NAÏVE BAYES
• Problema: Como derivar as probabilidades de x
pertencer a cada uma das categorias [p(x|F), p(x|E),
p(x|H)] a partir da tabela ?
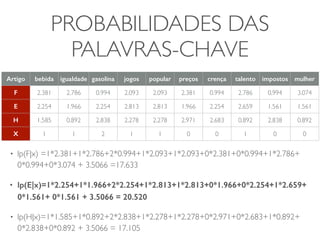
• Principio Naïve Bayes: assuma que as variáveis são
independentes em cada classe F, E e H
• Depois, calcular o produto das probabilidades f1, f2,
…,f10 de cada palavra chave em cada classe

19. CLASSIFICADOR NAÏVE BAYES
• Depois, calcular o produto das probabilidades f1, f2,…,f10 de cada
palavra chave em cada classe
• Dois problemas aqui:
• produto de muitos números bem menores que zero tende a 0
• se alguma das probabilidades for 0, o produto será 0
• Solução: substituir o produto por uma soma de logaritmos!

20. ALGORITMO NAÏVE BAYES
1. Calcule as probabilidades anteriores p(k), k=1, 2,…,K
2. Calcule as probabilidades de cada uma das m palavras
chaves em cada uma das k classes fk1, fk2,…, fkm
3. Calcule o logarítimo de p(x|k), lp(x|k) = x1log(fk1) +
x2log(fk2) + … + xmlog(fkm)
4. Calcule as somas lp(k|x) = log(p(k)) + lp(x|k) e atribua x
a classe k com lp(k|x) máximo

21. PROBABILIDADES DA
PALAVRAS-CHAVE
Artigo bebida igualdad
e
gasolina jogos popular preços crença talento imposto
s
mulher
F1 1 2 0 1 2 0 0 0 0 2
F2 0 0 0 1 0 1 0 2 0 2
F3 0 2 0 0 0 0 0 1 0 2
F4 2 1 0 0 0 2 0 2 0 1
• Primeira questão: como tratar as palavras gasolina, crença
e imposto ?
• Segunda questão: que probabilidade atribuir a palavra
mulher? Como considerar múltiplas ocorrência ?

22. PROBABILIDADES DA
PALAVRAS-CHAVE
Artigo bebida igualdad
e
gasolina jogos popular preços crença talento imposto
s
mulher
F1 1 2 0 1 2 0 0 0 0 2
F2 0 0 0 1 0 1 0 2 0 2
F3 0 2 0 0 0 0 0 1 0 2
F4 2 1 0 0 0 2 0 2 0 1
• Modelo da sacola de palavras: por todas as palavras em um saco.
• Somar as ocorrências de todas as palavras na classe
(3+5+0+2+2+3+0+5+0+7 = 27) com o total de palavras (10) = 37
• A probabilidade de uma palavra em uma é a sua quantidade de ocorrências
+ 1 dividida pelo total de palavras da classe.

23. PROBABILIDADES DAS
PALAVRAS-CHAVE
Artigo bebida igualdade gasolina jogos popular preços crença talento impostos mulher
F 0.108 0.162 0.027 0.081 0.081 0.108 0.027 0.162 0.027 0.216
E 0.095 0.071 0.095 0.167 0.167 0.071 0.095 0.143 0.048 0.048
H 0.049 0.024 0.171 0.098 0.098 0.195 0.146 0.024 0.171 0.024
• Por exemplo, fbebida,E=(3+1)/(32+10)=4/42 =0.095
• Há 3 ocorrências da palavra bebida na classe E e 32 palavras em
todos os artigos dessa classe, portanto, 42 é o tamanho da sacola
de palavras para a classe E.

24. PROBABILIDADES DAS
PALAVRAS-CHAVE
Artigo bebida igualdade gasolina jogos popular preços crença talento impostos mulher
F 2.381 2.786 0.994 2.093 2.093 2.381 0.994 2.786 0.994 3.074
E 2.254 1.966 2.254 2.813 2.813 1.966 2.254 2.659 1.561 1.561
H 1.585 0.892 2.838 2.278 2.278 2.971 2.683 0.892 2.838 0.892
• Calculando o logaritmo natural das probabilidades
(*100 para deixar tudo positivo)

25. PROBABILIDADES DAS
PALAVRAS-CHAVE
Artigo bebida igualdade gasolina jogos popular preços crença talento impostos mulher
F 2.381 2.786 0.994 2.093 2.093 2.381 0.994 2.786 0.994 3.074
E 2.254 1.966 2.254 2.813 2.813 1.966 2.254 2.659 1.561 1.561
H 1.585 0.892 2.838 2.278 2.278 2.971 2.683 0.892 2.838 0.892
X 1 1 2 1 1 0 0 1 0 0
• Calcule o logaritmo da probabilidade de um documento pertencer a cada classe
(C=log(100/3) = 3.5066
• Considere o vetor x e calcule o produto interno dele com cada linha da tabela
• Some C a cada resultado
• X pertence a classe com o maior valor resultante

26. PROBABILIDADES DAS
PALAVRAS-CHAVE
Artigo bebida igualdade gasolina jogos popular preços crença talento impostos mulher
F 2.381 2.786 0.994 2.093 2.093 2.381 0.994 2.786 0.994 3.074
E 2.254 1.966 2.254 2.813 2.813 1.966 2.254 2.659 1.561 1.561
H 1.585 0.892 2.838 2.278 2.278 2.971 2.683 0.892 2.838 0.892
X 1 1 2 1 1 0 0 1 0 0
• lp(F|x) =1*2.381+1*2.786+2*0.994+1*2.093+1*2.093+0*2.381+0*0.994+1*2.786+
0*0.994+0*3.074 + 3.5066 =17.633
• lp(E|x)=1*2.254+1*1.966+2*2.254+1*2.813+1*2.813+0*1.966+0*2.254+1*2.659+
0*1.561+ 0*1.561 + 3.5066 = 20.520
• lp(H|x)=1*1.585+1*0.892+2*2.838+1*2.278+1*2.278+0*2.971+0*2.683+1*0.892+
0*2.838+0*0.892 + 3.5066 = 17.105

27. ÁRVORE DE DECISÃO
7 erros 6 erros

28. ÁRVORE DE DECISÃO
• Árvore de classificação
construída a partir de um
conjunto de treinamento
com particionamento alvo H
• Objetivo: construir um
particionamento G com
similaridade máxima com H
• Início: G composto por um
único agrupamento, o
conjunto de dados
6 erros

29. ÁRVORE DE DECISÃO
• Um particionamento é
escolhido como o melhor
dentre todos os
particionamentos possíveis
• Um função de score avalia a
similaridade entre a partição
alvo H e a partição G em
construção
6 erros

30. EXEMPLO DE CONSTRUÇÃO
DE UMA ÁRVORE DE
DECISÃO PARA A IRIS

31. AVALIANDO UM CLASSIFICADOR
• Considere a seguinte tabela de resultados de um
aparelho capaz de diagnosticar cancer de pulmão
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim 94 7 101
Não 1 98 99
Total 95 105 200
• Acurácia de 96%!
• E daí?

32. AVALIANDO UM CLASSIFICADOR
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim 2 2 4
Não 1 195 196
Total 3 197 200
• Existem dois tipos de erros: 7 falsos positivos e 1
falso negativo.
• Ambos são igualmente graves ?

33. AVALIANDO UM CLASSIFICADOR
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim 2 2 4
Não 1 195 196
Total 3 197 200
• Podem haver diferenças entre os casos
identificados corretamente quando a amostra é
desbalanceada

34. AVALIANDO UM CLASSIFICADOR
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim 2 2 4
Não 1 195 196
Total 3 197 200
• Acurácia de 98.5%!
• Porém, 1/3 dos pacientes com câncer foram
diagnosticados incorretamente com câncer e 1/2
dos pacientes com câncer não foram diagnosticados!

35. AVALIANDO UM CLASSIFICADOR
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim TP FP TP + FP
Não FN TN FP + TN
Total TP + FN FN + TN Tudo
• Acurácia = (TP + TN)/Tudo
• Precisão = TP / (TP+FP) - Classificador
• Recall = TP / (TP+FN) - Classificação

36. AVALIANDO UM CLASSIFICADOR
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim 2 2 4
Não 1 195 196
Total 3 197 200
• Acurácia = (TP + TN)/Tudo = 98.5%
• Precisão = TP / (TP+FP) = 2 / 4 = 50%
• Recall = TP / (TP+FN) = 2 / 3 = 67%
• Como combinar Precisão e Recall?

37. AVALIANDO UM CLASSIFICADOR
Paciente realmente com
Sim câncer Não Total
Diagnóstico
da máquina
Sim 2 2 4
Não 1 195 196
Total 3 197 200
• Acurácia = (TP + TN)/Tudo = 98.5%
• Precisão = TP / (TP+FP) = 2 / 4 = 50%
• Recall = TP / (TP+FN) = 2 / 3 = 67%
• F = 2 /((1/Precisão) + (1/Recall)) = 2 / ( ( 1/0.5) + (1/0.67)) = 0.57

38. AVALIANDO UM CLASSIFICADOR
EXEMPLO: AVALIANDO
NOSSO CLASSIFICADOR DE
IRIS