Estatística

ESTATÍSTICA
Edite Manuela da G.P. Fernandes
Universidade do Minho, Braga, 1999

ESTATÍSTICA
com a colaboração de
A. Ismael F. Vaz
na realização dos gráﬁcos
Universidade do Minho, Braga, 1999

Título: Estatística
Autor: Edite Manuela da G.P. Fernandes
Composição: Texto preparado em LATEX por A. Ismael F. Vaz
Impressão da capa, fotocópias e montagem: Serviços de Reprograﬁa e Publicações da
Universidade do Minho
Capa: A. Ismael F. Vaz
TEX é uma marca registada da American Mathematical Society.
100 exemplares em Janeiro de 1999

Conteúdo
Prefácio iv
I Estatística descritiva 1
1 Introdução 2
1.1 O que é a Estatística . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Aplicações . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.3 População e Amostras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.4 Tipos de Estatística . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2 Descrição numérica dos dados 6
3 Descrição gráﬁca dos dados 12
4 ”Estatísticas” descritivas 21
4.1 Medidas de tendência central . . . . . . . . . . . . . . . . . . . . . . . . . 21
4.2 Medidas de dispersão . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
4.3 Medidas de associação . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
5 Distribuição normal 31
6 Análise de Regressão 34
6.1 Regressão Linear e Simples . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
6.2 Regressão não linear . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
II Séries cronológicas 36
7 Componentes do estudo 37
7.1 Representação gráﬁca de uma série cronológica . . . . . . . . . . . . . . . . 37
7.2 Estudo de uma série cronológica . . . . . . . . . . . . . . . . . . . . . . . . 37
8 Decomposição 39
i

CONTEÚDO ii
9 Estudo da tendência 40
9.1 Métodos para estudo da tendência . . . . . . . . . . . . . . . . . . . . . . . 40
9.1.1 Método das médias móveis . . . . . . . . . . . . . . . . . . . . . . . 41
9.1.2 Método analítico . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
10 Movimento sazonal 46
10.1 Método para determinar as flutuações sazonais . . . . . . . . . . . . . . . . 47
10.1.1 Método das médias mensais . . . . . . . . . . . . . . . . . . . . . . 47
III Estatística demográfica 49
11 Estruturas populacionais 50
11.1 Taxas de crescimento . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
11.2 Cálculo das densidades populacionais . . . . . . . . . . . . . . . . . . . . . 54
11.3 Estruturas demográficas . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
11.3.1 Pirâmides de idades . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
11.3.2 Grupos funcionais . . . . . . . . . . . . . . . . . . . . . . . . . . . . 58
12 Qualidade dos dados 60
12.1 Relação de masculinidade . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
12.2 Índice de Whipple . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
12.3 Índice de irregularidade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 62
12.4 Índice combinado das Nações Unidas . . . . . . . . . . . . . . . . . . . . . 62
12.5 A equação da concordância . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
13 Análise da mortalidade 65
13.1 Taxa bruta de mortalidade . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
13.2 Tipos particulares de mortalidade . . . . . . . . . . . . . . . . . . . . . . . 67
13.3 Tábua de mortalidade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
14 Análise da natalidade e da fecundidade 74
15 Análise da nupcialidade 79
15.1 Taxas de nupcialidade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
15.2 Tábua de nupcialidade . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
16 Análise dos movimentos migratórios 85
16.1 Métodos directos de análise . . . . . . . . . . . . . . . . . . . . . . . . . . 85
16.2 Métodos indirectos de análise . . . . . . . . . . . . . . . . . . . . . . . . . 86

CONTEÚDO iii
IV Exercícios 88
Tabela de números aleatórios 105

Prefácio
Este trabalho está dividido em quatro partes e tem como objectivo servir de apoio às aulas
teóricas e teórico-práticas da disciplina anual de Estatística do mestrado em História das
Populações.
A primeira parte faz uma breve introdução à Estatística descritiva. Além de serem in-
troduzidos conceitos relacionados com a descrição gráfica de dados, é também apresentado
um capítulo sobre as medidas mais importantes de tendência central, de dispersão e de
associação entre dados.
Na segunda parte são introduzidos e estudados alguns aspectos importantes das séries
cronológicas, designadamente a tendência e a sazonalidade.
A terceira parte trata da Estatística demográfica. Não só são referidas medidas ele-
mentares para a análise da Qualidade dos dados, como também são apresentadas taxas
e outras medidas de análise das variáveis microdemográficas mais importantes, nomeada-
mente a mortalidade, natalidade, fecundidade e nupcialidade.
Na última parte são incluídos enunciados de trabalhos práticos de apoio às aulas teórico-
práticas.
Braga, Outubro de 1998
iv

Parte I
Estatística descritiva
1

Capítulo 1
Introdução
Embora a palavra estatística ainda não existisse no ano 3 000 A.C. há indícios de que nessa
altura já se faziam censos na Babilónia e no Egipto. A palavra censo deriva de "censere",
que em latim significa taxar. Na era romana o imperador César Augusto ordenou que se
fizesse um censo em todo o império.
A palavra estatística deriva de ”status”, que em latim significa estado. Sob esta palavra
os Estados têm acumulado dados relativos ao seu povo. A estatística nas mãos dos governos
tem sido uma ferramenta essencial para a definição das suas políticas.
1.1 O que é a Estatística
O termo estatística tem várias interpretações.
Para a maioria das pessoas estatística emprega-se para designar informação em termos
de números. Não usaremos o termo estatística com este significado. A estas quantidades
numéricas daremos o nome de observações ou dados.
O termo estatística tem ainda outros significados. A Estatística é um ramo da área da
matemática aplicada com os seus próprios simbolismos, terminologia, conteúdo, teoremas
e técnicas. Quando estudamos Estatística estamos a tentar conhecer e dominar as suas
técnicas. Assim, podemos definir a Estatística como uma ciência matemática que agrega
um conjunto de técnicas apropriadas para a recolha, a classificação, a apresentação e a
interpretação de dados numéricos.
Um outro significado para a palavra é o da ”estatística” que está relacionada com
quantidades que forem calculadas a partir de dados amostrais. Neste caso é costume
colocar a palavra entre aspas. Por exemplo, se os dados obtidos forem: 12, 12, 14, 15, 12
e 13, a quantidade 12+12+14+15+12+13
6
, conhecida por média aritmética, é uma ”estatística”.
1.2 Aplicações
As aplicações das técnicas estatísticas estão já tão difundidas e a sua influência tem sido
tão marcante, que a importância da Estatística é já hoje em dia reconhecida em todos os
2

CAPÍTULO 1. INTRODUÇÃO 3
domínios da investigação científica e do desenvolvimento tecnológico.
Uma das áreas onde a Estatística começou a ser aplicada mais cedo foi no planeamento
e na análise de experiências realizadas na agricultura. A metodologia da Estatística tem
sido muito usada na investigação realizada pelas indústrias farmacêutica e médica. As
próprias instituições governamentais usam a Estatística para estudar a situação económica
do País e alterar as políticas de cobrança de impostos, de assistência social, de obras
públicas, etc. A teoria das probabilidades juntamente com a Estatística, isto é, a teoria
da decisão estatística, é usada como um meio para a tomada de decisões importantes ao
mais alto nível. Usamos as técnicas estatísticas na indústria para o controlo da qualidade
dos produtos, no ’marketing’, no estudo dos efeitos da publicidade, e também em todas as
áreas onde é preciso tomar decisões tendo como base informação incompleta, tal como na
Biologia, Geologia, Psicologia e Sociologia. Nas políticas educacionais a Estatística é uma
ferramenta muito importante para ajudar a definir pedagogias e métodos de ensino.
1.3 População e Amostras
Dois dos termos mais usados em Estatística são: população e amostra.
População designa um conjunto de unidades com qualquer característica comum. Por
exemplo, o conjunto das idades das crianças da Escola Preparatória XXX da cidade YYY
constitui uma população; o conjunto de todas as classificações obtidas, na disciplina de
Matemática, pelas crianças do 5o
¯
ano de escolaridade das Escolas Preparatórias do País
constitui uma população.
A Estatística ocupa-se fundamentalmente das propriedades das populações susceptíveis
de representação numérica.
A população pode ser finita ou infinita, consoante seja finito ou infinito o número
de elementos que a compõem. Para conhecer bem as propriedades da população temos
de analisar todos os elementos dessa população. Contudo, nem sempre é possível analisar
todos os elementos. Esta impossibilidade pode dever-se ao facto de a população ser infinita.
O estudo incidirá, assim, sobre um subconjunto finito de elementos que seja representativo
da população. Este subconjunto chama-se amostra.
A representatividade da amostra é uma das questões mais importante relacionada com
a teoria da amostragem. A amostra deve conter qualitativa e quantitativamente em pro-
porção tudo o que a população possui.
A amostra tem de ser também imparcial, isto é, todos os elementos da população devem
ter igual oportunidade de serem escolhidos para fazerem parte da amostra.
Mesmo quando a população é finita podem surgir outras razões que levem à utilização
de amostras para o estudo da população. Existem razões económicas - pode tornar-se
caro a observação do comportamento de um número muito grande de elementos; razões
de tempo - a observação de todos os elementos pode demorar tanto tempo que quando os
resultados estiverem prontos para divulgação já se encontrem desactualizados.
Existem, ainda, outras razões que nos levam a preferir recolher uma amostra em vez de
usar a população. Nalguns casos, as unidades que constituem a amostra para inspecção,

são destruídas. Noutros casos, em virtude da escassez de pessoas treinadas (sem forma-
ção específica) para recolher amostras, é mais seguro confiar num número reduzido de
informação. Haveria uma menor ocorrência de erros humanos.
Parece, assim, ser mais vantajoso recolher amostras e basear o nosso estudo na análise
dessas amostras. Este processo parece ser bastante simples, no entanto, pode dar origem
a enganos.
A selecção de elementos da população que são mais facilmente acessíveis ao experimen-
tador, origina uma amostra conveniente. Este tipo de amostra não é representativa da
população e pode levar a conclusões erradas sobre as propriedades da população.
Uma alternativa à amostra conveniente, que é muitas vezes parcial, é a amostra ale-
atória simples.
A ideia principal consiste em dar a cada elemento da população a mesma oportunidade
de ser escolhido para fazer parte da amostra. Para abreviar usaremos, daqui para a frente,
a.a.s. para designar amostra aleatória simples.
Uma a.a.s. é obtida através de um método que dá a qualquer possível amostra de
tamanho n (com n elementos) a mesma oportunidade de ser a amostra escolhida.
Dos métodos existentes, o mais usado e simples para a obtenção de uma a.a.s. consiste
em:
• usar uma tabela de números aleatórios como a que está representada na tabela da
figura 1.1. (ou um gerador de números aleatórios como têm algumas máquinas de
calcular, normalmente designado pela função RND). Uma tabela de números alea-
tórios é uma lista dos 10 dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 que satisfaz as seguintes
propriedades:
1. Um dígito em qualquer posição da lista tem a mesma oportunidade de ser o 0,
1, 2, 3, 4, 5, 6, 7, 8 ou 9.
2. Os dígitos nas diferentes posições são independentes no sentido de que o valor
de um deles não influencia o valor de qualquer outro.
A tabela apresenta uma divisão dos números por grupos de 5 dígitos e tem as linhas
numeradas, com o objectivo de facilitar a consulta. Para usar a tabela devemos ter em
atenção o seguinte:
1. Qualquer par de dígitos da tabela tem a mesma oportunidade de ser (qualquer) um
dos 100 possíveis pares 00, 01, 02, 03, ..., 97, 98, 99.
2. Qualquer trio de dígitos na tabela tem a mesma oportunidade de ser um dos 1000
possíveis trios 000, 001, 002, 003, ..., 997, 998, 999.
3. E assim por adiante, para grupos de 4 ou mais dígitos da tabela. Os grupos de 4
dígitos seriam os seguintes: 0000, 0001, 0002, ..., 0997, 0998, ..., 9997, 9998, 9999.
Para a selecção de uma a.a.s. usamos o seguinte processo:

linha
101 19223 95034 05756 28713 96409 12531 42544 82853
102 73676 47150 99400 01927 27754 42648 82425 36290
103 45467 71709 77558 00095 32863 29485 82226 90056
104 52711 38889 93074 60227 40011 85848 48767 52573
105 95592 94007 69971 91481 60779 53791 17297 59335
Figura 1.1: Parte da tabela de números aleatórios (ver Anexo)
1. enumerar os elementos da população a partir do 0 (se existirem até 10 elementos
na população), do 00 ( se existirem até 100 elementos na população), do 000 (se
existirem até 1000 elementos na população) ou ..., até esgotar todos os elementos;
2. seleccionar o tamanho da amostra;
3. retirar da tabela da figura 1.1, a partir de qualquer linha, grupos de 1, 2, 3 ou ...
dígitos (consoante o número de elementos da população), todos seguidos. Cada grupo
selecciona o elemento da população com aquele número.
Nota 1.3.1 :
• Sempre que aparecerem grupos de 1, 2, 3 ou ... (conforme o caso) dígitos repetidos,
devemos ignorá-los.
• Sempre que aparecerem grupos de 1, 2, 3 ou ... dígitos que sejam quantidades maiores
ou iguais que o número de elementos da amostra, devemos ignorá-los.
1.4 Tipos de Estatística
Podemos dividir a Estatística em dois grupos: a Estatística Descritiva e a Estatística
Inferencial.
A primeira toma indistintamente a população e a amostra com o objectivo de as des-
crever. Esta descrição das observações pode ser feita gráfica ou numericamente. Será uma
descrição gráfica se for feita a representação gráfica de certas quantidades calculadas a
partir das observações. A descrição diz-se numérica se forem calculadas quantidades que
dão informação, embora sumária, do comportamento das observações. A análise estatística
feita no século passado e no príncipio deste século foi na maior parte do tipo descritivo.
A Estatística tem sido definida como a ciência para a tomada de decisões baseadas
em incertezas, isto é, baseadas num conjunto de informações incompletas. Para tomarmos
decisões sobre a população, seleccionamos uma amostra aleatória simples retirada da po-
pulação. Baseando-nos na informação obtida da amostra inferimos sobre as características
da população. A Estatística Inferencial baseia-se no estudo das amostras para podermos
tirar conclusões sobre a população donde retirámos essas amostras.

Capítulo 2
Descrição numérica dos dados
A ideia que muitas pessoas têm da Estatística é a de que ela está associada a tabelas
enormes de números, por vezes documentadas com alguns gráficos à mistura! As tabelas
repletas de informação são muitas vezes cansativas de ler, difíceis de interpretar e de se tirar
conclusões e alguns gráficos mal dimensionados e legendados podem originar interpretações
erradas.
Mesmo assim, as tabelas são um dos meios mais usados para organizar e resumir um
conjunto vasto e desordenado de dados (ou observações). É mais vantajoso contruir uma
tabela pequena com algumas quantidades especiais ("estatísticas"da amostra ou parâme-
tros da população) que caracterizam e resumem a distribuição (o comportamento) dessas
observações, do que uma tabela com um conjunto enorme de números. Os gráficos têm
como objectivo dar uma visão resumida e rápida do comportamento dos dados.
Consideremos o seguinte ficheiro de dados da Escola Preparatória XXX da cidade YYY.
Para cada aluno, foram registados os seguintes valores das variáveis: SEXO (feminino ou
masculino), IDADE (10, 11, 12, 13, 14 ou 15 anos), ALTURA (de 129 cm. a 145 cm.),
PESO (de 27 kg. a 45 kg.), ANO (5o
ou 6o
ano de escolaridade) e TURMA (1, 2, 3, 4
ou 5). A maior parte das tabelas e gráficos apresentados nesta parte I dizem respeito aos
valores deste ficheiro.
Dado um conjunto de observações, é costume, em primeiro lugar, contar quantas vezes
aparece cada valor, isto é, o número de ocorrências desse valor. Dos 318 alunos presente-
mente a frequentar a Escola Preparatória XXX da cidade YYY,
• quantos são do sexo feminino?
• quantos são do sexo masculino?
• quantos frequentam, neste ano lectivo, o 5o
ano de escolaridade?
• quantos estão inscritos no 6o
ano de escolaridade?
• quantos alunos do 5o
ano têm ainda 10 anos?
• quantos alunos frequentam o 6o
ano com 15 anos de idade?
6

CAPÍTULO 2. DESCRIÇÃO NUMÉRICA DOS DADOS 7
Depois de observados todos os registos e contadas as ocorrências dos seis acontecimentos
descritos, obtivemos os seguintes valores, conhecidos por frequências absolutas : 124
alunos do sexo feminino, 194 do sexo masculino, 147 do 5o
ano, 171 do 6o
ano, como se
SEXO Frequências Percentagens F.Acumulada
feminino 124 38.99 38.99
masculino 194 61.01 100.00
Total 318 100.00
ANO Frequências Percentagens F.Acumulada
5o
ano 147 46.23 46.23
6o
ano 171 53.77 100.00
Total 318 100.00
Figura 2.1: Tabelas de frequências do SEXO e do ANO de escolaridade
pode ver na coluna indicada por ’Frequências’ da tabela da figura 2.1; 73 alunos estão
no 5o
com 10 anos e 9 no 6o
com 15 anos. Confirme estes valores com os assinalados
da coluna ’Frequências’ da tabela da figura 2.2. Verificando-se que 124 + 194 = 318 ou
147 + 171 = 318 conclui-se que foram consideradas todas as observações (consistência
interna).
A frequência absoluta de qualquer valor de uma variável é o número de vezes que
esse valor ocorre nos dados. Isto é, esta frequência corresponde a uma contagem.
Observando apenas o número 124 de alunos do sexo feminino e 194 do sexo masculino
podemos dizer que há mais rapazes do que raparigas, no entanto, não se vê logo quantos
mais. Se compararmos estes números com o número total de alunos, calculando o quociente
entre o número total de alunos do sexo feminino (ou do sexo masculino) e o número total
de alunos da escola, a que chamaremos frequência relativa, então já podemos dizer que
124
318
= 0.39 (ou 194
318
= 0.61) são do sexo feminino (ou masculino) o que é nitidamente menos
(ou mais) do que metade dos alunos.
A frequência relativa de qualquer valor é a proporção ou fracção de todas as observa-
ções que têm aquele valor. Esta frequência pode ser expressa em termos de percentagem,
multiplicando a fracção resultante por 100 e atribuindo o sinal de %. Das fracções an-
teriores tiramos 39% de alunos do sexo feminino e 61% do sexo masculino. A soma das
frequências relativas deve ser igual a 1 (ou das percentagens igual a 100%).
Veja as percentagens de alunos dos dois sexos na coluna indicada por ’Percentagens’
da tabela da figura 2.1.
As frequências acumuladas absolutas (ou relativas) representam o número (ou a
fracção/percentagem) de observações que são menores ou iguais a um valor especificado.
Assim o número (ou fracção/percentagem) de alunos com idade inferior a 12, do 5o
ano de
escolaridade é de 118 (ou 0.8027/80.27%) e o número (ou fracção/percentagem) de alunos
do 6o
ano com idade igual ou inferior a 14 anos é de 162 (ou 0.9474/94.74%), como se pode
confirmar pela coluna ’F.Acumuladas’ da tabela da figura 2.2.

ANO=5o
IDADE Frequências Percentagens F.Acumuladas
10 73 49.66 49.66
11 45 30.61 80.27
12 22 14.97 95.24
13 4 2.72 97.96
14 3 2.04 100.00
Total 147 100.00
ANO=6o
11 91 53.22 53.22
12 46 26.90 80.12
13 20 11.70 91.81
14 5 2.92 94.74
15 9 5.26 100.00
Total 171 100.00
Figura 2.2: Tabela de frequências da IDADE, por ANO de escolaridade
Da coluna ’F.Acumuladas’ da tabela da figura 2.3 podemos verificar que o número de
alunos do 6o
ano que têm um peso igual ou inferior a 40 Kg. é de 161, o que corresponde
a 94.15% dos alunos desse ano.
Da coluna ’F.Acumuladas’ da tabela da figura 2.4 podemos concluir que a percentagem
de alunos do sexo feminino com altura igual ou inferior a 140 cm. é aproximadamente de
91%.
As frequências absolutas e as relativas são um meio muito usado para classificar os
dados quando a escala usada para medir as variáveis é nominal, isto é, a medição da
variável apenas define a classe a que o elemento pertence. Por exemplo, a variável SEXO
é nominal, uma vez que ela é definida pelas duas classes: feminino e masculino; a variável
ANO de escolaridade é nominal e as classes definidas são o 5o
e o 6o
ano de escolaridade;
a variável TURMA é também nominal, definida pelas classes 1, 2, 3, 4 e 5 para o 5o
ano
de escolaridade e 1, 2, 3, 4 e 5 para o 6o
ano.
Certas variáveis são medidas de acordo com uma escala ordinal. Neste caso a medição
define classes e ordena-as de acordo com os valores atribuídos. Como exemplo, temos as
pontuações (1, 2, 3, ... e 10) que hoje se usam para definirmos a nossa preferência relativa
a qualquer acontecimento. A diferença entre o 2 e o 1 é a de que o 2 significa ter preferência
em relação ao 1 mas não se sabe quanto.
Mesmo quando a escala de medição da variável é intervalar/proporcional e a variável
pode tomar uma quantidade enorme de valores, podemos classificar (resumir) os dados
calculando as frequências de grupos de valores, chamados classes ou intervalos. Quando a
medida de uma variável nos diz quanto ela é diferente da medida de outra, então a variável

ANO=5o
Classes
de pesos Frequências Percentagens F.Acumuladas
peso <=30 34 23.13 23.13
30 a 35 74 50.34 73.47
35 a 40 33 22.45 95.92
40 a 45 6 4.08 100.00
Total 147 100.00
ANO=6o
Classes
de pesos Frequências Percentagens F.Acumuladas
peso <=30 46 26.90 26.90
30 a 35 77 45.03 71.93
35 a 40 38 22.22 94.15
40 a 45 10 5.85 100.00
Total 171 100.00
Figura 2.3: Tabela de frequências dos PESOS, por ANO de escolaridade
foi medida numa escala intervalar. Por exemplo, uma avaliação baseada na escala de 0 a
20 é intervalar; uma classificação de 14.4 valores é nitidamente superior a uma de 7.2, no
entanto, 14.4 não significa um desempenho duas vezes melhor do que o 7.2. A medição
duma variável numa escala proporcional diz-nos quanto ela tem a mais em relação a outra.
Por exemplo, a ALTURA e o PESO dos alunos são exemplos de variáveis proporcionais.
Um peso de 46 Kg. é duas vezes superior ao peso de 23 Kg.
Quando temos este tipo de variáveis devemos decidir quantas classes/intervalos quere-
mos formar. Quando temos poucas observações devemos definir um número pequeno de
classes, 4, 5 ou 6. No entanto, quando o número de observações é elevado menos do que 10
classes origina uma perda significativa de informação. Tudo depende também da variação
dos valores que a variável pode tomar. Assim como o número de intervalos e a amplitude
desses intervalos são arbitrários, também o são os pontos que definem o início, limite
inferior, e o fim, limite superior, de cada intervalo. Estes limites separam os intervalos
uns dos outros. Eles devem ser escolhidos por forma a que, para cada observação, fique
bem claro a que intervalo ela pertence. Por exemplo, relativamente à variável ALTURA,
podemos usar um dos dois seguintes processos:
1. o primeiro intervalo, para a variável ALTURA, compreende os valores que vão desde
125 a 130 cm. inclusivé ( isto é, 125 < ALTURA ≤ 130); o segundo intervalo terá
observações desde 130 cm. até 135 cm. inclusivé (130 < ALTURA ≤ 135), ....,
até ao último intervalo que engloba ALTURAS que vão desde os 145 aos 150 cm.
(145 < ALTURA ≤ 150);

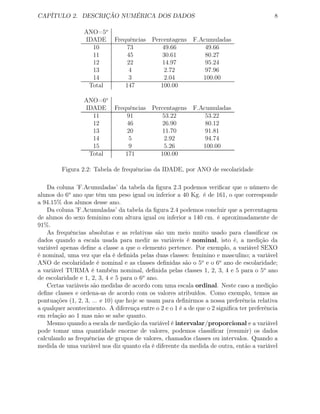
SEXO=feminino
Classes
de alturas Frequências Percentagens F.Acumuladas
altura<=130 5 4.03 4.03
130 a 135 42 33.87 37.90
135 a 140 66 53.23 91.13
140 a 145 10 8.06 99.19
altura>145 1 0.31 100.00
Total 124 100.00
SEXO=masculino
Classes
de alturas Frequências Percentagens F.Acumuladas
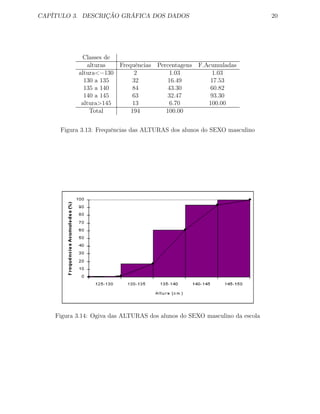
altura<=130 2 1.03 1.03
130 a 135 32 16.49 17.53
135 a 140 84 43.30 60.82
140 a 145 63 32.47 93.30
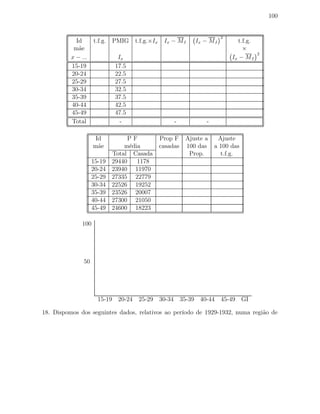
altura>145 13 6.70 100.00
Total 194 100.00
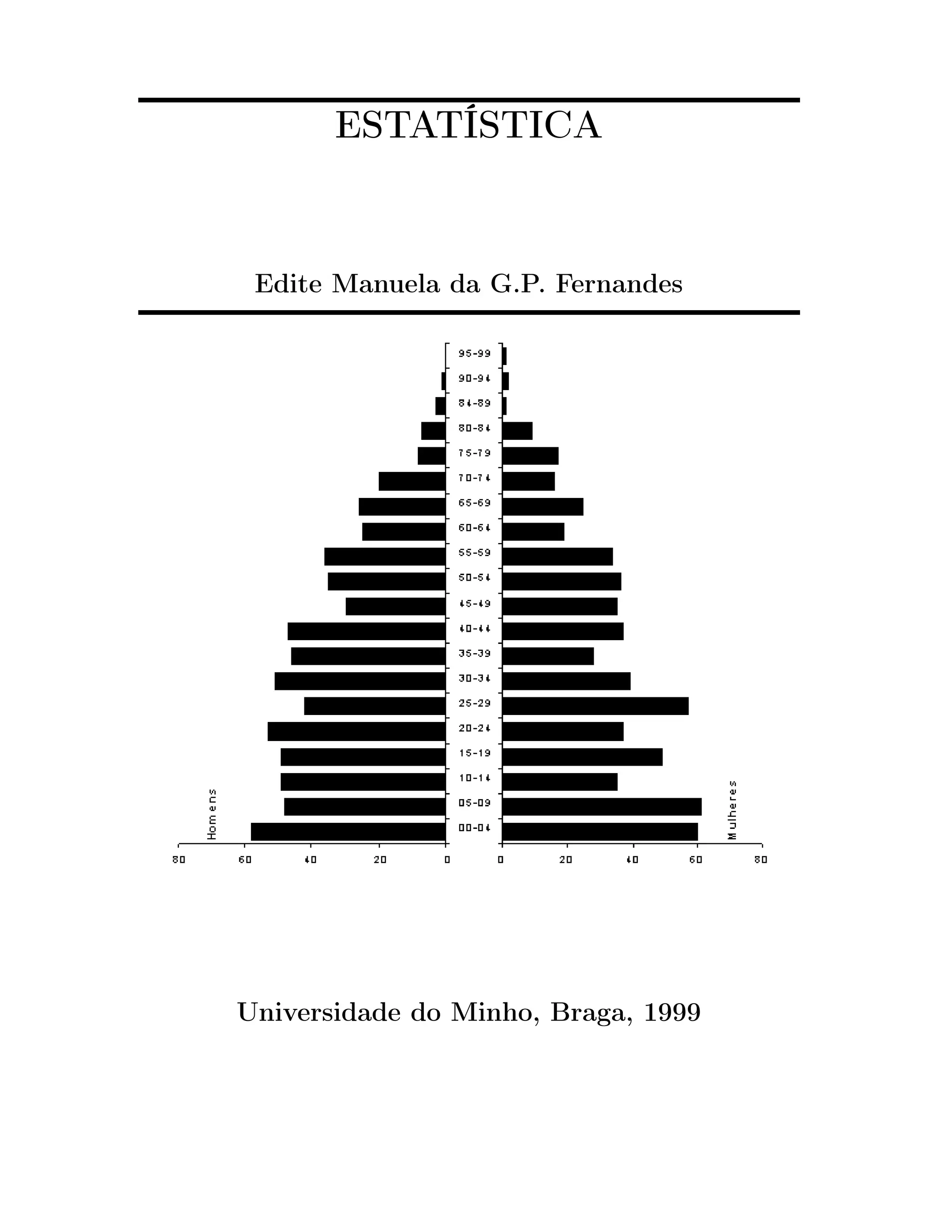
Figura 2.4: Tabela das frequências das ALTURAS, por SEXO do aluno
2. (e como, para esta variável, todas as observações são quantidades inteiras) os limi-
tes dos intervalos são definidos usando valores com casas decimais, 0.5 unidades
inferiores ao valor, para o limite inferior, e 0.5 unidades superiores ao valor, para o
limite superior, de cada intervalo. Neste caso, ficamos com os seguintes intervalos
fechados nos dois extremos: [124.5, 130.5], [130.5, 135.5], [135.5, 140.5], [140.5, 145.5]
e [145.5, 150.5].
É também comum considerar os intervalos dos extremos como ’totalmente’ abertos, o
primeiro à esquerda, e o último à direita, isto é, o primeiro intervalo pode ser do tipo
≤ 130cm. e o último do tipo > 145cm. Verifique o processo utilizado na definição dos
intervalos para a variável ALTURA, na tabela da figura 2.4 e para a variável PESO na
tabela da figura 2.3.
A amplitude destas classes/intervalos é a diferença entre o limite superior e o inferior.
Para a variável ALTURA a amplitude dos intervalos é de 5 cm. e para o PESO é de 5 Kg.
Confirme estes valores nas tabelas das figura 2.4 e 2.3 respectivamente.
Como estes intervalos são definidos por um conjunto, por vezes, vasto de valores, há
necessidade de ter um valor que represente cada intervalo. Este valor é o ponto médio e
calcula-se como a semi-soma dos limites superior e inferior do intervalo. No caso da variável
ALTURA os pontos médios dos intervalos são respectivamente 127.5, 132.5, 137.5, 142.5 e
147.5 e para a classificação da variável PESO temos como pontos médios os valores: 27.5,

32.5, 37.5, 42.5. Repare que os intervalos dos extremos foram considerados como tendo
amplitudes iguais aos restantes.
O número de observações que pertencem a cada classe/intervalo é a sua frequência
absoluta. Tudo o que já foi dito relativamente às frequências relativas e acumuladas é
válido para estas classes/intervalos.

Capítulo 3
Descrição gráfica dos dados
Um gráfico serve para dar uma visão resumida dos dados. Um gráfico bem construído pode
revelar factos (características) sobre os dados que, a retirar de uma tabela necessitariam
de uma análise mais cuidada.
1. O gráfico de barras serve para comparar a frequência de ocorrência de certas
observações.
Na maior parte dos exemplos, os valores comparados são frequências absolutas ou
relativas, em termos de percentagem, de variáveis medidas de acordo com as escalas
nominal e ordinal. A figura 3.1 apresenta um gráfico de barras respeitante aos dados
Gráfico de barras
0
20
40
60
80
100
120
140
10 11 12 13 14 15
IDADE
Frequência
Figura 3.1: Gráfico de barras das frequências das IDADES dos alunos
12

CAPÍTULO 3. DESCRIÇÃO GRÁFICA DOS DADOS 13
10 73 22.96 22.96
11 136 42.77 64.72
12 68 21.38 87.11
13 24 7.55 94.65
14 8 2.52 97.17
15 9 2.83 100.00
Total 318 100.00
Figura 3.2: Tabela de frequências das IDADES dos alunos da Escola
As barras aparecem normalmente verticais, separadas e devem ter todas a mesma
largura. A altura da barra varia com a frequência, o que significa que a área do
rectângulo também varia. A nossa percepção da quantidade representada, corres-
ponde precisamente à área da barra.
Um gráfico de barras pode ser representado através de figuras a que se pode dar o
nome de gráfico ilustrativo ou pictograma. No entanto, essas figuras devem defi-
nir imagens todas com a mesma largura, variando a altura com o valor da frequência.
Nas figuras 3.3 e 3.4 estam representados dois exemplos de gráficos de barras utili-
zando figuras. O primeiro não está correcto, pois pode levar a falsas interpretações
em termos relativos; o segundo, que é tão atraente como o primeiro, está correcto. As
áreas das figuras visualizam correctamente as proporções relativas entre as variáveis.
Figura 3.3: Pictograma (errado) da variável SEXO (ver tabela da figura 2.1)

Figura 3.4: Pictograma da variável SEXO (ver tabela da figura 2.1)
2. O gráfico de sectores ou circular serve para representar várias variáveis. O tama-
nho de cada sector é proporcional ao valor da variável, que representa, em relação à
soma dos valores das variáveis lá representadas.
Assim e tendo em conta os alunos do 5o
ano de escolaridade, verificamos que há
números diferentes de alunos dos sexos feminino e masculino nas diferentes turmas,
como se pode ver na tabela da figura 3.5 e os gráficos de sectores correspondentes
seriam os representados nas figuras 3.6 e 3.7.
3. Existe ainda outro gráfico de barras, para representar várias variáveis, só que desta
vez elas apresentam-se sobrepostas. Dos mesmos valores da tabela da figura 3.5, o
gráfico de barras sobrepostas é o que está representado na figura 3.8.
4. O gráfico de linha serve para representar os valores de uma variável e mostra a
tendência (comportamento) dessa variável normalmente em relação ao tempo. Por
exemplo, se fosse conhecido o número de alunos inscritos na Escola XXX durante
os útimos dez anos, poderíamos representar esses valores ao longo do eixo vertical e
ao longo do eixo horizontal, representaríamos o tempo de acordo com o que está na
figura 3.9.
As escalas podem ser iniciadas em qualquer valor, em vez de 0. Para chamar a
atenção da omissão do 0, é frequente utilizar uma linha em ziguezague sobre o eixo.
5. Um gráfico de pontos serve para representar dados relativos a duas variáveis,
quando elas são medidas em escalas intervalar/proporcional ou ordinal. Cada variável

ANO=5o
Turma
SEXO 1 2 3 4 5 Total
feminino 10 7 12 7 14 50
masculino 24 22 14 21 16 97
Total 34 29 26 28 30 147
ANO=6o
Turma
SEXO 1 2 3 4 5 Total
feminino 17 16 15 11 15 74
masculino 20 18 18 24 17 97
Total 37 34 33 35 32 171
Figura 3.5: Frequências dos alunos do 5o
ano por TURMA
é representada num eixo. Cada ponto do gráfico corresponde a um par de valores
(x, y); x diz respeito ao valor da 1a
variável ( sobre o eixo das abcissas) e y diz respeito
ao correspondente valor da 2a
variável (sobre o eixo das ordenadas). Por exemplo,
se quiséssemos representar os PESOS e as ALTURAS dos alunos do SEXO feminino
da TURMA 2 do 5o
ANO da Escola XXX teríamos o gráfico que está representado
na figura 3.10.
6. O histograma das frequências é o gráfico mais importante na Estatística Inferen-
cial.
Quando os dados são valores de uma variável medida numa escala intervalar/proporcional,
uma tabela de frequências para cada uma das classes mostra a distribuição de valo-
res dessa variável. Considere o exemplo apresentado na tabela da figura 2.4 relativo
às ALTURAS dos alunos da Escola XXX, distribuídos por SEXO. Esta distribuição
pode ser representada graficamente num histograma. Este gráfico é desenhado tendo
como base um par de eixos coordenados, com a medida da variável que foi observada
colocada ao longo do eixo horizontal e o número ou a proporção de observações me-
didos ao longo do eixo vertical. O eixo vertical começa normalmente em 0 e o eixo
horizontal pode começar num valor qualquer, desde que seja conveniente.
A figura 3.11 mostra o exemplo em que as ALTURAS estão divididas por classes,
também chamadas intervalos de amplitudes iguais a 5 cm. Cada barra representa
uma dessas classes e a altura corresponde à frequência absoluta (número de valores
que pertencem à classe). Também se usam as frequências relativas ou proporções na
definição de histogramas.
Os histogramas têm as barras verticais, umas a seguir às outras e devem ser todas
da mesma largura. Assim, ao agrupar um conjunto de dados por classes para repre-

fe m inino
20
14
24
14
29
1
2
3
4
5
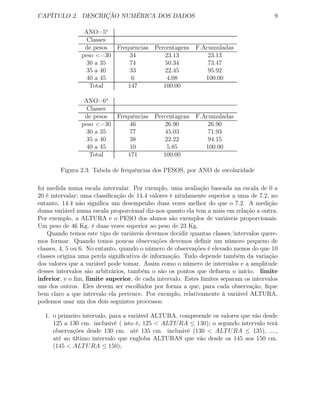
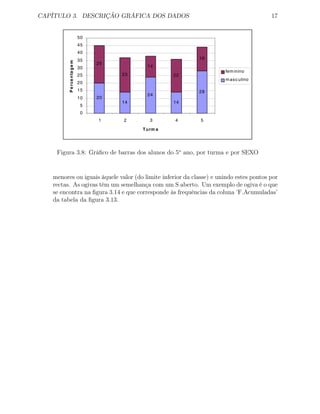
Figura 3.6: Gráfico de sectores dos alunos do 5o
ano do sexo feminino, por TURMA
]../pictures/sectoresm.eps
Figura 3.7: Gráfico de sectores dos alunos do 5o
ano do sexo masculino, por TURMA
sentar um histograma, devemos escolher intervalos (classes) com amplitudes iguais.
Não existe nenhum valor ideal para a amplitude da classe (intervalo). O objectivo
é conseguir obter uma distribuição de frequências equilibrada. Assim, tenta-se evi-
tar colocar todos os valores num número muito reduzido de classes de amplitudes
enormes ou distribuir poucos valores por muitas classes de amplitudes pequenas. As
classes devem ser definidas de tal forma que não haja ambiguidades sobre a classe
(ou intervalo) a que pertence cada observação.
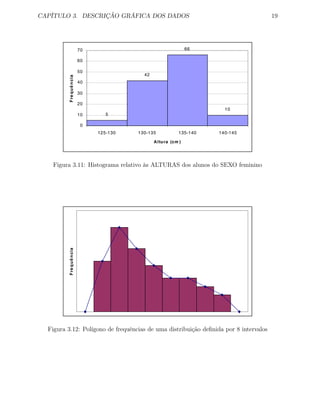
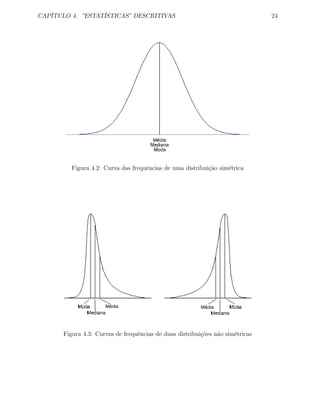
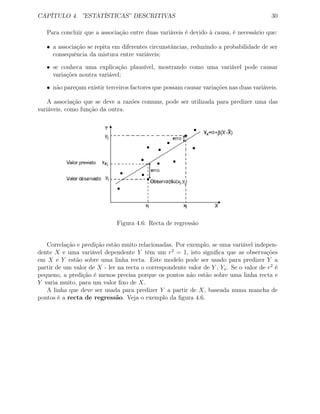
7. A forma da distribuição de frequências de um conjunto de dados pode ser analisada
através do histograma das frequências. A figura 3.12 mostra uma distribuição não
simétrica e descaída para a direita. Por vezes, a análise é facilitada pelo polígono que
se obtém unindo, por linhas, os pontos médios dos topos das barras no histograma,
como se vê na figura 3.12. O polígono é terminado para a esquerda e para a direita,
unindo os pontos que se colocam no eixo horizontal distanciados de metade da am-
plitude para a esquerda do primeiro intervalo e para a direita do último intervalo.
Este polígono é conhecido por polígono de frequências.
8. Ao gráfico das frequências acumuladas chama-se ogiva. Este gráfico obtém-se co-
locando pontos na vertical dos limites inferiores das classes (ou intervalos) a uma
distância do eixo horizontal que corresponde à percentagem das observações que são

20
14
24
14
28
25
23
14
22
16
0
5
10
15
20
25
30
35
40
45
50
1 2 3 4 5
Turm a
Percentagem feminino
m asculino
Figura 3.8: Gráﬁco de barras dos alunos do 5o
ano, por turma e por SEXO
menores ou iguais àquele valor (do limite inferior da classe) e unindo estes pontos por
rectas. As ogivas têm um semelhança com um S aberto. Um exemplo de ogiva é o que
se encontra na ﬁgura 3.14 e que corresponde às frequências da coluna ’F.Acumuladas’

220
240
250
265
270
280
295
309
315 318
200
220
240
260
280
300
320
83/84 84/85 85/86 86/87 87/88 88/89 89/90 90/91 91/92 92/93
te m po (a no le ctivo)
Númerodealunosinscritos
Figura 3.9: Gráﬁco relativo ao número de alunos da Escola, nos últimos dez anos
132
134
136
138
140
142
144
25 30 35 40 45
P e so (kg)
Altura(cm)
Figura 3.10: Gráﬁco relativo aos PESOS e ALTURAS dos 7 alunos da TURMA 2 (5o
ANO)

5
42
66
10
0
10
20
30
40
50
60
70
125-130 130-135 135-140 140-145
Altura (cm )
Frequência
Figura 3.11: Histograma relativo às ALTURAS dos alunos do SEXO feminino
Frequência
Figura 3.12: Polígono de frequências de uma distribuição deﬁnida por 8 intervalos

Classes de
alturas Frequências Percentagens F.Acumuladas
altura<=130 2 1.03 1.03
130 a 135 32 16.49 17.53
135 a 140 84 43.30 60.82
140 a 145 63 32.47 93.30
altura>145 13 6.70 100.00
Total 194 100.00
Figura 3.13: Frequências das ALTURAS dos alunos do SEXO masculino
Figura 3.14: Ogiva das ALTURAS dos alunos do SEXO masculino da escola

Capítulo 4
”Estatísticas” descritivas
Além das tabelas e dos gráﬁcos, que têm com objectivo organizar e dar uma imagem visual
dos dados, existem certas características de uma distribuição de valores, como o valor
central e a sua dispersão, que podem ser resumidas por meio de certas quantidades.
Exemplos destas quantidades, conhecidas por "estatísticas"descritivas, são: o ponto
médio, a mediana, a moda, a média, a amplitude, o desvio padrão e a variância.
4.1 Medidas de tendência central
1. o ponto médio é o valor que se encontra a meio caminho entre a menor e a maior
das observações de uma lista. Por deﬁnição
Xm =
menor obs. + maior obs.
2
.
Considerando a tabela 4.1 relativa às ”estatísticas” das IDADES dos alunos da Escola
XXX, o Xm é igual a 10+15
2
= 12.5.
2. A média (aritmética) de um conjunto de n observações obtém-se somando todas
as observações e dividindo depois pelo seu número.
Se X1, X2, X3, ..., Xn forem as n observações, então a média deste conjunto é
¯X =
n
i=1 Xi
n
.
Quando os dados estão agrupados por classes numa tabela de frequências, a soma de
observações idênticas é equivalente a multiplicar o valor dessa observação, Xi, pela
sua frequência fi. Assim, a média pode ser calculada através de
¯X =
k
i=1 fiXi
n
,
21

CAPÍTULO 4. ”ESTATÍSTICAS” DESCRITIVAS 22
IDADE
Percentis Menores
1% 10 10
5% 10 10
10% 10 10 Observações 313
25% 11 10 Soma dos pesos 313
50% 11 Média 11.3239
Maiores Desvio padrão 1.150557
75% 12 15
90% 13 15 Variância 1.32378
95% 14 15 Assimetria 1.162583
99% 15 15 Kurtose 4.48434
Figura 4.1: ”Estatísticas” das IDADES dos alunos da Escola
em que n = k
i=1 fi e k é o número de classes distintas. Quando cada classe é
representada por um intervalo de valores, o Xi é o valor que representa esse intervalo
e que anteriormente chamámos o ponto médio do intervalo. Se os intervalos dos
extremos são caracterizados por ≤ e >, os pontos médios são calculados do mesmo
modo, supondo que esses intervalos têm amplitudes iguais aos restantes. Da tabela
da ﬁgura 4.1, vemos que a média das IDADES dos 318 alunos da Escola XXX é de
11.3239.
3. A mediana é o valor típico, isto é, é o ponto central das observações quando elas
não estão agrupadas e já se encontram colocadas por ordem crescente.
Quando o número de observações é impar, o valor do meio é a mediana; quando o
número de observações é par, existe um par de valores no centro e a mediana passa
a ser a média aritmética desse par. Para o cálculo da mediana de um conjunto de
observações não agrupadas por classes ou intervalos, podemos usar a seguinte regra:
Se n for o número de observações, calcule a quantidade (n + 1)/2. Coloque as
observações por ordem crescente e conte a partir do início (n + 1)/2 observações. Se
n for impar a última contabilizada será a mediana da lista; se n for par, a quantidade
(n + 1)/2 não é inteira, e tomamos a semi-soma das duas observações contíguas a
esta quantidade (a anterior e a posterior) da lista.
Quando os n dados estão agrupados por k classes/intervalos, podemos usar o seguinte
processo para o cálculo da mediana:
• calcular n
2
,
• calcular as frequências absolutas acumuladas das classes,

• determinar o intervalo que contém a mediana. Seja M o número desse intervalo
(M é um inteiro de 1 a k). A frequência acumulada dos intervalos anteriores ao
do da mediana é FM−1. A frequência absoluta do intervalo da mediana é fM e
a acumulada é FM , e FM−1 < n
2
< FM ,
• calcular o número de observações que devemos tomar do intervalo da mediana
e que é igual a n
2
− FM−1,
• como existem fM observações no intervalo da mediana e considerando-as unifor-
memente distribuídas, o valor da mediana está a n/2−FM−1
fM
de distância do início
do intervalo da mediana que tem amplitude igual a A e cujo limite inferior é
liM . Assim,
mediana = liM +
n
2
− FM−1
fM
A.
Como num histograma as áreas dos rectângulos são proporcionais às frequências
dos respectivos intervalos, a linha vertical traçada no valor da mediana divide o
histograma em duas áreas iguais.
4. A moda é o valor mais frequente, isto é, o valor com maior frequência entre as
observações de uma lista. Para o cálculo da moda convém colocar as observações
por ordem crescente para se ver qual delas ocorre mais vezes. Essa observação é a
moda. A lista, neste caso, diz-se unimodal. Pode até haver mais do que uma moda.
Se duas ou mais observações ocorrem o mesmo número de vezes, então a lista diz-se
respectivamente bimodal ou multimodal.
Quando os dados se apresentam agrupados, a classe com maior frequência define a
classe da moda. Se cada classe for definida por um só valor, esse é a moda; se a classe
é definida por um intervalo de valores, o ponto que representa a classe, o ponto médio
dessa classe, é a moda. Tal como foi dito no parágrafo anterior podemos também
aqui ter mais do que uma moda ou mesmo não ter nenhuma.
Destas medidas centrais, a média e a mediana são as mais usadas. A mediana utiliza
informação relativa à ordem, não usando os valores numéricos das observações. A média,
por sua vez, usa esses valores numéricos, sendo por isso a mais usada.
As diferentes localizações da média, da mediana e da moda são mais facilmente visíveis
usando a curva das frequências desse conjunto de dados, o polígono de frequências. A moda
é o valor onde a curva é mais alta. A mediana é o valor que divide a área, compreendida
entre o eixo e a curva, em duas partes iguais; metade fica à esquerda da mediana e a outra
metade à direita. A média é o ponto central de uma distribuição simétrica.
Numa distribuição simétrica a moda coincide com a mediana e também com a média.
Veja a figura 4.2.
A figura 4.3 apresenta dois exemplos de distribuições não simétricas. A primeira é
assimétrica positiva e a segunda é assimétrica negativa. Repare na sequência de localização
das três medidas: moda, mediana e média.

Figura 4.2: Curva das frequências de uma distribuição simétrica
Figura 4.3: Curvas de frequências de duas distribuições não simétricas

Dos valores da tabela 4.1 podemos retirar a mediana, que é o percentil de ordem 50, e
é igual a 11 e de acordo com a tabela que foi apresentada na figura 3.1, a moda é também
11, uma vez que é o valor que tem maior frequência (136). Assim, esta distribuição das
IDADES dos alunos da Escola XXX da cidade YYY é assimétrica positiva. Confirme este
facto com o gráfico de barras já anteriormente apresentado na figura 3.1. Da tabela da
figura 4.1 o valor do parâmetro ’Assimetria’=1.162583, porque é positivo, significa que a
distribuição é assimétrica positiva. Se este valor fosse negativo, teríamos uma distribuição
assimétrica negativa.
4.2 Medidas de dispersão
As medidas centrais são importantes mas não fornecem a informação completa sobre o
conjunto das observações. Falta, pois, indicação sobre a dispersão desses valores.
Quando se usa a mediana para medir o centro de uma distribuição, é conveniente
fornecer elementos sobre a variação ou dispersão da distribuição, através dos percentis.
As medidas de dispersão mais usadas são: a variância e o desvio padrão. Devem
ser usadas quando a medida de tendência central usada for a média, pois elas medem a
dispersão em relação à média, como centro da distribuição.
1. O percentil de ordem p de um conjunto de valores (observações de uma variável)
é o valor abaixo do qual estão p por cento dos valores, estando os restantes acima
dele.
A mediana é o percentil de ordem 50, também conhecido por segundo quartil.
O percentil de ordem 25 chama-se primeiro quartil.
O percentil de ordem 75 chama-se terceiro quartil.
Um quarto das observações são menores do que o 1o
quartil, metade são menores do
que o 2o
e um quarto são maiores do que o 3o
quartil.
2. A amplitude de um conjunto de valores é definida como a diferença entre a maior
e a menor das observações e mede a dispersão total dos valores do conjunto.
3. A variância é a média aritmética dos quadrados dos desvios das observações em
relação à média.
Assim, se X1, X2, X3, ..., Xn forem n observações e se ¯X for a sua média, a variância
é calculada a partir de
s2
=
n
i=1(Xi − ¯X)2
n
.
Quando os dados estão agrupados por k intervalos, a variância é definida por
s2
=
k
i=1(fiX2
i )
n
− ¯X2

em que n = k
i=1 fi, k é o número de classes (ou intervalos), fi é a frequência da
classe i e Xi o valor que representa a classe i.
Quando as observações formam uma amostra aleatória simples de tamanho n, reti-
rada de uma população, a variância da amostra deve ser calculada usando n − 1 no
denominador do primeiro termo da expressão, em vez de n, e deve-se multiplicar o
segundo termo por n
(n−1)
.
Existem razões para esta escolha e têm a ver com o facto de esta ’estatística’ poder
ser usada para estimar a variância da população.
4. O desvio padrão é a raiz quadrada da variância. Utiliza-se s para designar o desvio
padrão.
A variância e o desvio padrão das IDADES são, retirados directamente da tabela da
ﬁgura 4.1, respectivamente ’Variância’= 1.32378 e ’Desvio padrão’= 1.150557.
Alguns comentários em relação a estas medidas:
(i) A variância é uma quantidade positiva ou nula. Será nula se todos os desvios forem
nulos e isto acontece quando todos os Xi forem iguais a ¯X (sendo todos iguais). Neste
caso, não existe dispersão.
(ii) Se as observações estão dispersas e existem de um e de outro lado da média, os desvios
das observações à esquerda da média são negativos e os desvios das observações à
direita são positivos. Estes desvios serão tanto maiores, em valor absoluto, quanto
mais afastadas as observações estiverem da média. Os quadrados dos desvios são
quantidades positivas e tanto maiores quanto maiores forem os desvios. Assim, se
os valores estão juntos, a variância é pequena; se eles estão dispersos, a variância é
grande.
(iii) Quando as observações são medidas numa unidade (por exemplo, centímetros, segun-
dos, gramas, ...), a variância vem nessa medida ao quadrado. No entanto, o desvio
padrão vem medido na mesma unidade das observações.
4.3 Medidas de associação
As medidas centrais e de dispersão fornecem informação básica relativa a dados univariados,
embora não completa. No entanto, se tivermos duas variáveis, as medidas referidas atrás.
não são suﬁcientes para as descrever. Normalmente estamos interessados numa possível
ligação entre as variáveis: - os valores das variáveis aumentam simultaneamente, como a
altura e o peso das pessoas, ou variam em sentidos opostos, como o número de cigarros
fumados por dia e a esperança de vida do fumador!
Diz-se que duas variáveis estão associadas se existe uma ligação directa entre as suas
variações,

• quando o aumento de uma variável tende a acompanhar o aumento de outra variável,
diz-se que a associação é positiva;
• quando o aumento de uma variável tende a acompanhar a diminuição de outra va-
riável, então as variáveis dizem-se associadas negativamente.
A associação é medida em termos médios. A associação faz sentido para variáveis
medidas em qualquer tipo de escala. Associação positiva ou negativa já só faz sentido
quando as variáveis forem medidas numa escala ordinal ou intervalar/proporcional.
1. Uma das medidas de associação é o coeficiente de correlação. Dadas n observa-
ções bivariadas nas variáveis X e Y , X1, X2, ..., Xn e Y1, Y2, ..., Yn, o coeficiente de
correlação r é definido por
r =
1
n
n
i=1(Xi − ¯X)(Yi − ¯Y )
sXsY
em que ¯X e ¯Y são as médias dos valores de X e de Y respectivamente e sX e sY os
desvios padrões das mesmas variáveis.
O numerador da expressão é a média dos produtos dos desvios de X e de Y , em
relação às correspondentes médias. O denominador é o produto dos desvios padrões
de X e de Y .
Interpretação de r:
• o coeficiente de correlação r mede a associação entre duas variáveis; é positivo
quando a associação é positiva e negativo quando a associação for negativa (o
valor de r é tanto maior quanto mais forte for a associação);
• o coeficiente de correlação toma sempre valores entre -1 e +1 (os desvios padrão
no denominador estandardizam o r, as unidades no numerador e denominador
são as mesmas, o que significa que r é adimensional);
• os valores extremos r = −1 e r = 1 indicam uma associação perfeita (r = −1
significa que os pontos pertencem a uma linha recta de declive negativo, isto é,
quando x aumenta, y diminui; r = 1 significa que os pontos pertencem a uma
linha recta com declive positivo, isto é, quando x aumenta, y também aumenta;
• o coeficiente de correlação mede a proximidade da mancha de pontos em relação
a uma linha recta (r mede uma associação linear).
A figura 4.4 mostra cinco casos com diferentes valores de r. O último caso refere-se a
uma situação onde não existe uma relação linear, embora exista outro tipo de relação.
2. Existe uma maneira de medir a associação linear através de uma quantidade r2
,
chamada coeficiente de determinação. Este coeficiente é a proporção da variância
de uma variável, que pode ser explicada pela dependência linear na outra variável.

Figura 4.4: Cinco casos de associação

Para compreender melhor o seu significado, considere os dois gráficos da figura 4.5.
No primeiro, existe uma associação perfeita linear com r = −1. A variável Y está
totalmente ligada à variável X; quando X varia, Y também varia e o ponto (X, Y )
move-se ao longo da linha. O conjunto dos 8 valores de Y tem uma grande variância;
mas esta variância é devida (explicada) à ocorrência dos diferentes valores de X,
levando consigo os valores de Y . A dependência linear em X explica toda a variação
em Y e r2
= 1.
Figura 4.5: Duas associações diferentes entre duas variáveis
No segundo gráfico, o conjunto dos 21 valores de Y também tem uma grande variância.
Alguma desta variância pode ser explicada pelo facto de a variação em X levar consigo
uma variação (em média) em Y .
O gráfico apresenta esta situação, mostrando os diferentes valores de Y que acompa-
nham os dois valores de X. Neste caso, r2
= +1 pois a associação entre X e Y explica
apenas parte da variação em Y . Esta parte é a fracção r2
da variância dos valores de Y
Neste exemplo, r2
= 0.49 e diz-se que 49 por cento da variância de Y é explicada pela
dependência linear de Y em relação a X.
O coeficiente r2
mede apenas a intensidade da associação e não nos diz nada sobre se
ela é positiva ou negativa.
A associação entre duas variáveis pode ser devida a três factores:
• ao factor causa, isto é, uma das variáveis origina (causa) variações na outra;
• à existência de outra(s) variável(eis) que origina(m) o aparecimento das duas (ou,
cuja variação causa variações nas duas) variáveis em estudo;
• a uma terceira variável, que não se encontra em estudo, mas que, juntamente com
uma das variáveis causa variações na outra.

Para concluir que a associação entre duas variáveis é devido à causa, é necessário que:
• a associação se repita em diferentes circunstâncias, reduzindo a probabilidade de ser
consequência da mistura entre variáveis;
• se conheca uma explicação plausível, mostrando como uma variável pode causar
variações noutra variável;
• não pareçam existir terceiros factores que possam causar variações nas duas variáveis.
A associação que se deve a razões comuns, pode ser utilizada para predizer uma das
variáveis, como função da outra.
Figura 4.6: Recta de regressão
Correlação e predição estão muito relacionadas. Por exemplo, se uma variável indepen-
dente X e uma variável dependente Y têm um r2
= 1, isto significa que as observações
em X e Y estão sobre uma linha recta. Este modelo pode ser usado para predizer Y a
partir de um valor de X - ler na recta o correspondente valor de Y , Yx. Se o valor de r2
é
pequeno, a predição é menos precisa porque os pontos não estão sobre uma linha recta e
Y varia muito, para um valor fixo de X.
A linha que deve ser usada para predizer Y a partir de X, baseada numa mancha de
pontos é a recta de regressão. Veja o exemplo da figura 4.6.

Capítulo 5
Distribuição normal
Quando um conjunto de dados tem uma distribuição descrita por uma das curvas normais,
a média é facilmente detectada. Esta distribuição é simétrica, a média coincide com a
mediana e também com a moda. É o valor que corresponde ao pico. Veja o gráfico da
figura 4.2.
O desvio padrão também é facilmente detectável da curva normal. Os pontos onde a
curvatura muda, de ambos os lados em relação ao centro, estão localizados a um desvio
padrão de cada lado da média. O gráfico da figura 5.1. apresenta três exemplos de
distribuições normais com a mesma média mas com diferentes desvios padrão.
Figura 5.1: Distribuições normais com diferentes desvios
A média fixa o centro da curva, enquanto que o desvio padrão determina a forma.
Alterando a média de uma distribuição normal não altera a forma, apenas altera a sua
localização nos eixos. No entanto, alterando o desvio padrão, a forma da curva é alterada.
31

CAPÍTULO 5. DISTRIBUIÇÃO NORMAL 32
Em todos os casos, temos a curva normal das frequências com uma amplitude igual a
seis desvios padrão.
Considere a ﬁgura 5.2. Em qualquer distribuição normal,
Figura 5.2: Distribuição normal
1. metade das observações são menores do que a média e a outra metade maiores;
2. 68 por cento das observações pertencem ao intervalo limitado por um desvio padrão
para cada lado da média; destas, metade (34 por cento) estão entre a média e um
desvio padrão para além da média;
3. 95 por cento das observações pertencem ao intervalo limitado por dois desvios para
cada lado da média;
4. 99.7 por cento das observações pertencem ao intervalo limitado por três desvios em
relação à média.
Em qualquer distribuição normal, o percentil de ordem 84 de uma distribuição normal
está localizado a um desvio padrão acima da média. Do mesmo modo o percentil de ordem
16 é o ponto localizado a menos um desvio padrão em relação à média.
As observações retiradas de diferentes distribuições normais podem ser comparadas,
colocando-as em unidades de desvio padrão acima ou abaixo da média. Observações ex-
pressas em unidades de desvio padrão em relação à média, chamam-se pontuações es-
tandardizadas (’standard’). Esta pontuação é calculada da seguinte maneira:
pontuação estandardizada =
observação − média
desvio padrão
.

CAPÍTULO 5. DISTRIBUIÇÃO NORMAL 33
Por exemplo, uma pontuação de 24 unidades num teste, cuja média foi de 18 e o desvio
padrão de 6, é equivalente a (24−18
6
=)1 unidade de pontuação estandardizada. Uma
pontuação estandardizada de 1 corresponde sempre ao percentil de ordem 84, qualquer
que seja a distribuição normal original.

Capítulo 6
Análise de Regressão
Seja Y uma variável aleatória dependente cuja variação é afectada pela variação da variável
independente X.
Sejam X1, X2, ..., Xn os valores escolhidos arbitrariamente para X e Yi(i = 1, ..., n) os
correspondentes valores de Y .
6.1 Regressão Linear e Simples
A partir dos valores observados, podemos estimar a recta de regressão linear e simples
(com uma só variável independente). A forma da recta é:
Yx = α + β(X − X)
em que X é a média aritmética dos n valores de X, X1, X2,... ,Xn e α e β são calculados
através de
α =
n
i=1 Yi
n
β =
n
i=1(Xi − X)(Yi − Y )
n
i=1(Xi − X)2
=
n
i=1(Xi − X)Yi
n
i=1(Xi − X)2
.
Embora seja possível fazer interpolação, isto é, calcular o valor de Y que corres-
ponde a um dado valor de X = X0, se este pertencer ao intervalo definido pelos valores
X1, X2, ..., Xn usados nos cálculos, a extrapolação deve ser implementada com cuidado
pois,
1. embora existindo uma relação linear entre X e Y (esta pode ser adequada na região
definida pelo conjunto de valores usados), o modelo pode deixar de ser válido fora da
região definida por esse conjunto,
2. quanto mais afastado X0 estiver de X, maior será o erro de extrapolação.
34

CAPÍTULO 6. ANÁLISE DE REGRESSÃO 35
6.2 Regressão não linear
Além do modelo de regressão linear, existem outros modelos que podem descrever a de-
pendência de Y em relação a X. Mesmo assim, a análise de regressão já definida pode ser
aplicada, desde que seja possível para isso redefinir as variáveis ou transformar a equação,
de modo a conseguir-se um modelo linear nos parâmetros.
Como primeiro exemplo, considere o caso em que
Y = α + βX2
.
A equação é já linear nos parâmetros α e β e a única não linearidade está na variável
independente X.
No segundo exemplo,
Yx = Xβ
,
mais complicado, a não linearidade envolve directamente o parâmetro β a ser calculado.
Esta equação exige uma transformação de variáveis que a torne linear em β.
Para o primeiro caso, o modelo matemático, no caso geral, é
Yx = α + βw + γw2
com w = W − W. Se fizermos x = w e z = w2
, este modelo reduz-se a um modelo linear
e múltiplo.
Para o segundo caso, se aplicarmos logaritmos, obtemos o modelo
ln Yx = β ln X ou yx = βx
que já é linear no parâmetro β, sendo, neste caso, x = ln X e y = ln Y . Este modelo é
agora linear e simples, sem constante α.

Parte II
Séries cronológicas
36

Capítulo 7
Componentes do estudo
Comecemos pela definição:
Definição 7.0.1 Uma série cronológica é um conjunto de observações feitas em períodos
sucessivos de tempo, durante um certo intervalo.
Exemplo 7.0.1 Valores da taxa bruta de natalidade, em anos sucessivos.
Exemplo 7.0.2 Percentagem da população com idade inferior a 7 anos, em anos suces-
sivos.
Vamos designar o conjunto dessas observações por X1, X2, ..., Xn e vamos supor que
foram feitas nos períodos de tempo t1, t2, ..., tn contados a partir de uma origem fixada.
As observações são normalmente feitas em períodos de tempo igualmente espaçados.
7.1 Representação gráfica de uma série cronológica
Para iniciar a análise de uma série cronológica deve representar-se graficamente as ob-
servações. Esta representação gráfica chama-se cronograma. Nos eixos das ordenadas
marca-se o valor da série. No eixo das abcissas marca-se o tempo (ver figura 7.1)
7.2 Estudo de uma série cronológica
Duas das questões mais importantes a ter em conta no estudo de uma série cronológica
são:
• A comparação entre valores da série se o intervalo entre tempos não é constante.
Pode ser ultrapassada fazendo uma correcção aos valores da série.
• A variação da população a que se refere o fenómeno. As variações sofridas ao longo
do tempo que sejam devidas à variação no número de elementos da população não
interessam. A análise das variações deve ser feita em termos relativos.
37

CAPÍTULO 7. COMPONENTES DO ESTUDO 38
0
1
2
3
4
5
6
t1 t2 t3 t4 t5 t6 t7 t8
tem po
valordasérie
cronogram a
Figura 7.1: Gráfico de uma série cronológica
Constata-se que na maior parte das séries cronológicas as sucessivas observações não
são independentes. Por exemplo, o valor da observação no instante t3 depende dos valores
nos instantes t1 e t2.
Quando se verifica dependência é possível prever valores futuros tendo como base valores
da série já observados.
O estudo de uma série cronológica consiste na descrição, na explicação, na previsão e
no controlo dessa série. Assim,
• a descrição consiste na caracterização do comportamento através da identificação
de pontos altos e baixos, distância entre eles, valores aberrantes e pontos de viragem;
• a explicação compreende a formulação de hipóteses e a tentativa de construir um
modelo matemático que permita descrever o comportamento da série até ao presente;
• a previsão estabelece uma relação entre o comportamento observado da série e o
comportamento futuro;
• o controlo é um fenómeno que tenta modificar o comportamento futuro da série.

Capítulo 8
Decomposição
Algumas séries cronológicas são influenciadas por uma ou duas causas dominantes. Outras
são influenciadas por uma infinidade de causas.
É conveniente decompor as séries cronológicas em componentes que se agrupam em:
movimentos sistemáticos



tendência (’trend’)
movimento sazonal
movimento oscilatório
movimentos não sistemáticos movimento aleatório
• A tendência é a variação em média, ao longo do tempo (compreende os movimen-
tos que se manifestam suave e consistentemente ao longo de um período grande de
tempo).
• Os movimentos sazonais são variações em relação à tendência que ocorrem, em
geral, dentro de um ano.
Os movimentos sazonais podem ter causas naturais e causas sociais.
– As causa naturais estão associadas (quase sempre) com as estações do ano.
– As causa sociais estão associadas com usos, costumes e tradições sociais.
• Os movimentos oscilatórios ocorrem mais em séries económicas e associam-se a
ciclos económicos de expansão e depressão. Não apresentam periodicidade definida.
Estes são difíceis de separar da tendência.
• Os movimentos aleatórios são de carácter fortuito, irregulares e de origem desco-
nhecida.
Exemplos: guerras, epidemias, greves, secas, ...
Para o estudo da série é aconcelhável identificar e limitar primeiro a tendência, depois
os movimentos sazonais e finalmente as oscilações.
39

Capítulo 9
Estudo da tendência
A tendência é um movimento suave e consistente ao longo de um período grande de tempo
(o termo grande é relativo pois o que é grande para uma série pode ser pequeno para
outra). O número de anos em que se deve considerar a tendência varia de série para série.
Algumas causas da presença da tendência numa série cronológica são:
• causas relacionadas com variações na população;
• causas relacionadas com idade, saúde, educação, constituição, conhecimentos teóricos
da população;
• causas relacionadas com a qualidade e quantidade de recursos.
Estas causas estão relacionadas entre si.
Os objectivos a atingir com a determinação da tendência são:
1. Estudá-la para extrapolar como forma de prever o comportamento da série no futuro;
2. Eliminá-la para estudar as outras componentes (sazonalidade, oscilação e aleatorie-
dade).
Quando se elimina a tendência, a série diz-se estacionária.
9.1 Métodos para estudo da tendência
Os dois métodos mais importantes para estudar a tendência são:
1. Método das médias móveis
2. Método analítico
40

CAPÍTULO 9. ESTUDO DA TENDÊNCIA 41
9.1.1 Método das médias móveis
O método das médias móveis consiste em calcular a média aritmética de observações
contidas em escalões, tomando-a como estimativa do valor local da tendência. Assim, as
etapas a seguir são:
1. começa-se por dividir a série em escalões, com igual número de termos sobrepostos;
• o número de observações em cada escalão chama-se período da média móvel,
(ver ﬁgura 9.1)
x x x x x x x x x x
Figura 9.1: Escalões de período igual a 3
• Se tem k observações em cada escalão, existem k − 1 observações em comum
com os escalões seguintes (e anteriores).
2. Calculam-se as estimativas locais da tendência;
• Se k é impar (k = 2m + 1):
as estimativas da tendência são (exemplo com k = 3, m = 1)
t2 =
X1 + X2 + X3
3
t3 =
X2 + X3 + X4
3
t4 =
X3 + X4 + X5
3
...
tn−1 =
Xn−2 + Xn−1 + Xn
3
e a tendência não é estimada para os primeiros e últimos m pontos do tempo.
• Se k é par (k = 2m)

i) as estimativas da tendência calculam-se em pontos médios de um intervalo
(exemplo com k = 4, m = 2)
ponto médio de [2, 3] =
X1 + X2 + X3 + X4
4
X2 + X3 + X4 + X5
4
X3 + X4 + X5 + X6
4
...
ii) para centrar estas médias, calcula-se uma 2a
média móvel de período 2
[2, 3] = X1+X2+X3+X4
4
[3, 4] = X2+X3+X4+X5
4
⇒
t3 =
X1+X2+X3+X4
4
+ X2+X3+X4+X5
4
2
.
Do mesmo modo
t4 =
X2+X3+X4+X5
4
+ X3+X4+X5+X6
4
2
, ...
O método das médias móveis é um caso particular dos filtros lineares, filtros esses que
transformam uma série X noutra Y , por meio de uma operação linear.
9.1.2 Método analítico
Com o método analítico a determinação da tendência é feita ajustando uma função da
variável tempo (t) ao cronograma da série cronológica.
Este ajuste é feito, em geral, pelo método dos mínimos quadrados.
De acordo com o tipo de função assim podemos ter tendências lineares, parabólicas,
exponenciais, ...
A função vai traduzir uma lei matemática que se admite ser seguida pela tendência.
A escolha do tipo de função a ajustar não é fácil e este processo deve ser iniciado com
a representação gráfica da série e inspecção cuidada do cronograma.
Tendência linear
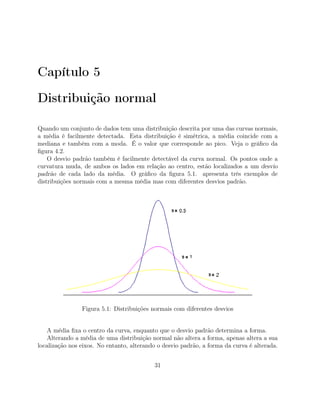
O modelo mais simples que é possível representar é o modelo linear com a seguinte
forma:
Xt = α + βt. (9.1)
Como
Xt = α + β(t − t) = α + βt − βt = α − βt + βt,

tem-se
α = α − βt (9.2)
em que t é a média aritmética dos tempos, t1, t2, ..., tn, e os valores de α e β são calculados
da seguinte maneira:
α =
X1 + X2 + ... + Xn
n
(9.3)
e
β =
(t1 − t)X1 + (t2 − t)X2 + ... + (tn − t)Xn
(t1 − t)2 + (t2 − t)2 + ... + (tn − t)2
. (9.4)
O valor de α da equação Xt = α + βt chama-se ordenada na origem, isto é, quando
t = 0, Xt = α, e β representa o declive da recta. Este declive dá a variação verificada
em Xt quando t varia de um período de tempo (constante).
O quadrado do coeficiente de correlação das duas variáveis X e t, r2
(coeficiente de
determinação) dá a percentagem da variação da série original explicada pela tendência
linear. A diferença 100% − r2
% é a variação explicada pelos outros movimentos.
Além da tendência linear, descrita por um polinómio linear, existem outros tipos, tais
como: tendências quadráticas (polinómio quadrático), tendências cúbicas (polinómio cú-
bico), exponenciais, etc.
Exemplo 9.1.1 Considere a seguinte tabela de valores [2]:
Ano t X desvios:X − Xt
1973 1 233 41.258
1974 2 250.3 39.884
1975 3 158 -71.09
1976 4 178.3 -69.464
1977 5 293.5 27.062
1978 6 309.5 24.388
1979 7 279 -24.786
1980 8 355.2 32.74
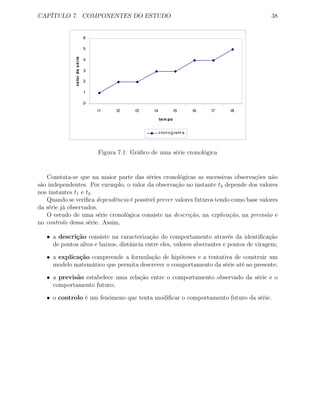
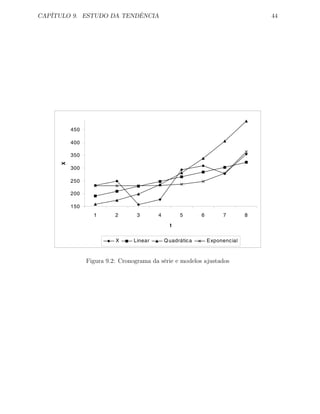
O cronograma está representado na figura 9.2.
No ajuste de uma tendência linear, usando as equações (9.3), (9.4), (9.2) e finalmente
(9.1), obtêm-se
Xt = 173.068 + 18.674 t.
A representação desta recta está na figura 9.2. A interpretação é a seguinte - A partir
de uma valor de 173.068 verificado para t = 0 (1972), a tendência (Xt) aumenta (β > 0),
em média, por ano (ver 1a
coluna da tabela) 18.67.
Se calcularmos o coeficiente de determinação, r2
, teremos r2
= 0.475, ou seja, 47.5%
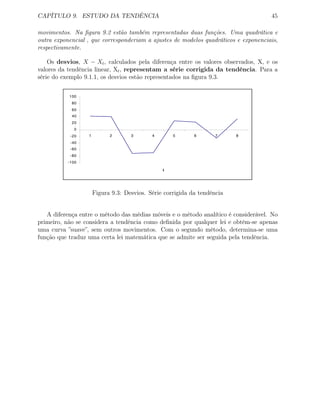
da variação da série original é explicada pela tendência, ficando 52.5% à conta dos outros

150
200
250
300
350
400
450
1 2 3 4 5 6 7 8
t
X
X Linear Quadrática Exponencial
Figura 9.2: Cronograma da série e modelos ajustados

movimentos. Na figura 9.2 estão também representadas duas funções. Uma quadrática e
outra exponencial , que corresponderiam a ajustes de modelos quadráticos e exponenciais,
respectivamente.
Os desvios, X − Xt, calculados pela diferença entre os valores observados, X, e os
valores da tendência linear, Xt, representam a série corrigida da tendência. Para a
série do exemplo 9.1.1, os desvios estão representados na figura 9.3.
-100
-80
-60
-40
-20
0
20
40
60
80
100
1 2 3 4 5 6 7 8
t
Figura 9.3: Desvios. Série corrigida da tendência
A diferença entre o método das médias móveis e o método analítico é considerável. No
primeiro, não se considera a tendência como definida por qualquer lei e obtém-se apenas
uma curva ”suave”, sem outros movimentos. Com o segundo método, determina-se uma
função que traduz uma certa lei matemática que se admite ser seguida pela tendência.

Capítulo 10
Movimento sazonal
Os movimentos sazonais são variações que ocorrem dentro de um ano e de acordo com
um certo modelo (mais ou menos rígido) que se repete de ano para ano.
São todos os movimentos periódicos de período igual ou inferior a um ano.
Exemplo 10.0.2 Sazonalidade de casamentos[1] (índices)
Paróquias
Mês Sul do Pico Transmontanas Guimarães
Jan 122 126 117
Fev 164 172 160
Mar 29 91 64
Abr 52 111 118
Mai 140 131 127
Jun 105 98 111
Jul 73 64 64
Ago 69 68 76
Set 93 83 78
Out 154 75 96
Nov 161 78 110
Dez 39 104 94
Deste exemplo é visível que a marcação de casamentos, nalgumas regiões, é afectada
por:
• razões sociais: respeito pelas interdições da Quaresma, Advento
• razões económicas: fainas agrícolas, preparação das vinhas (ﬁm de inverno), vindi-
mas, pastagens no verão.
46

CAPÍTULO 10. MOVIMENTO SAZONAL 47
10.1 Método para determinar as ﬂutuações sazonais
10.1.1 Método das médias mensais
O termo mensal está relacionado com o facto do período sazonal ser de um ano e estar
dividido em meses. Neste caso deve-se trabalhar com médias mensais.
Se o ciclo for outro, por exemplo, o ano dividido em trimestre deve-se trabalhar com
médias trimestrais.
O método das médias mensais só deve aplicar-se a uma série quando os dados não
apresentarem tendência ou quando esta não for muito pronunciada. Existindo tendência,
esta viciará os índices. Assim, o método das médias mensais só deve ser aplicado depois
de se ter eliminado a tendência.
Se a tendência foi estimada através do ajuste de uma recta, Xt = α + βt (ver (9.1)), os
desvios em relação à tendência traduzem a série corrigida da tendência e é a partir destes
valores corrigidos que se calculam os índices sazonais.
As etapas do método são as seguintes:
1. Dispôr as observações num quadro da seguinte maneira:
mêsano 1900 1901 1902 ... Total Média Índice
Jan ...
Fev ...
Mar ...
Abr ...
Mai ...
Jun ...
Jul ...
Ago ...
Set ...
Out ...
Nov ...
Dez ...
Total ...
(este exemplo refere-se a um período dividido em meses)
2. Calcular os totais (somas) referentes aos meses e colocá-los na coluna referenciada
com Total;
3. Calcular as médias para cada mês e colocá-las na coluna referenciada por Média;
4. Calcular a média das médias (média geral) e colocá-la na última célula da coluna
”Média”;

CAPÍTULO 10. MOVIMENTO SAZONAL 48
5. Os índices sazonais são calculados como a percentagem da média de cada mês em
relação à média geral.
Nota 10.1.1 A soma dos índices é 1200.
Nota 10.1.2 O nível que traduz ausência de sazonalidade é igual a 100.
Assim, os índices são interpretados da seguinte maneira:
• Um valor menor que 100 indica que nesse mês a ﬂutuação sazonal se traduz numa
quebra em relação ao nível ’normal’ (100);
• Um valor maior que 100 indica um aumento em relação ao nível normal.
Nota 10.1.3 Também existe o método das médias móveis para estudar a sazonalidade [2].

Parte III
Estatística demográﬁca
49

Capítulo 11
Estruturas populacionais
Iremos estudar alguns dos aspectos globais da população através do seu volume, ritmo de
crescimento e densidade.
11.1 Taxas de crescimento
Quando temos, ao longo do tempo, informação variada sobre o volume de uma população
queremos numa primeira análise calcular o ritmo de crescimento. O valor do ritmo de
crescimento deve corresponder a um resultado anual médio para ser possível fazer compa-
rações em períodos de amplitudes diferentes. O ritmo de crescimento de uma população
pode ser
i) Contínuo:
com
Pn = P0ean
(11.1)
onde:
e = 2.718282 (exponencial)
Pn =população num momento n
P0 =população num momento 0
a =taxa de crescimento.
Aplicando logaritmos neperianos (ln) a (11.1) temos
ln Pn = ln P0 + ln ean
ln Pn − ln P0 = an
ln
Pn
P0
= an
50

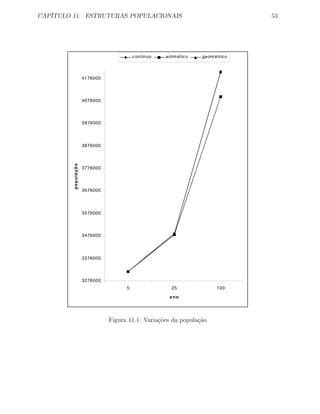
CAPÍTULO 11. ESTRUTURAS POPULACIONAIS 51
e
a =
ln Pn
P0
n
(11.2)
onde a corresponde à taxa de crescimento contínuo.
ii) Aritmético:
com
Pn = P0(1 + an)
ou seja
Pn = P0 + P0an
Pn − P0 = P0an
e
a =
Pn − P0
P0n
(11.3)
onde a corresponde à taxa de crescimento aritmético.
iii) Geométrico:
com
Pn = P0(1 + a)n
(11.4)
ou seja
Pn
P0
= (1 + a)n
(11.5)
e aplicando logaritmo na base 10 a (11.5) temos
log
Pn
P0
= n log(1 + a)
log(1 + a) =
log Pn
P0
n
,
ou seja
1 + a = 10
log
Pn
P0
n
e
a = 10
log Pn
P0
n − 1 (11.6)
onde a corresponde à taxa de crescimento geométrico.
Exemplo 11.1.1 Se em 1821 a população de uma região era de 3276203 habitantes, e se
a taxa de crescimento, a, é de 0.25%, qual a população ao ﬁm de 5, 25 e 100 anos?

i) Se for crescimento contínuo
P5 = 3276203e0.0025×5
= 3317412
P25 = 3276203e0.0025×25
= 3487500
P100 = 3276203e0.0025×100
= 4206728
ii) Se for crescimento aritmético
P5 = 3276203(1 + 0.0025 × 5) = 3317156
P25 = 3276203(1 + 0.0025 × 25) = 3480966
P100 = 3276203(1 + 0.0025 × 100) = 4095254
iii) Se for crescimento geométrico
P5 = 3276203(1 + 0.0025)5
= 3317361
P25 = 3276203(1 + 0.0025)25
= 3487228
P100 = 3276203(1 + 0.0025)100
= 4205416
(ver figura 11.1)
Exemplo 11.1.2 Análise prospectiva:
Se a taxa de crescimento geométrico for a = 0.0021 (0.21%), ao fim de quantos anos
(n?) duplicará a população?
Crescimento geométrico:
Pn = P0(1 + a)n
2P0 = P0(1 + a)n
2P0
P0
= (1 + a)n
2 = (1 + a)n
.
Aplicando logaritmos,
log 2 = n log(1 + a)
0.30103 = n log(1.0021)
0.30103 = n × 0.0009111
n =
0.30103
0.0009111
e
n = 330, 4...
R: ao fim de 330 anos

3276000
3376000
3476000
3576000
3676000
3776000
3876000
3976000
4076000
4176000
5 25 100
a no
população
contínuo aritmético geom étrico
Figura 11.1: Variações da população

Exemplo 11.1.3 Análise regressiva:
A população em 1821 era de 3276203 habitantes. Se admitirmos que o ritmo de cres-
cimento na primeira metade do sec XIX era de 0.0021 (a = 0.21%) qual teria sido a
população em 1801?
Sabe-se que em 1821, n = 20, Pn = P20 = 3276203. Considerando 1801 como o ano 0,
queremos saber P0 (com crescimento geométrico).
Pn = P0(1 + a)n
3276203 = P0(1 + 0.0021)20
3276203
P0
= (1 + 0.0021)20
.
Aplicando logaritmos,
log
3276203
P0
= 20 log(1.0021)
log
3276203
P0
= 0.01822.
Aplicando agora a função inversa, potência de 10,
3276203
P0
= 100.01822
3276203
P0
= 1.04285
e
P0 =
3276203
1.04285
= 3141586.
11.2 Cálculo das densidades populacionais
Para calcular a densidade populacional de uma certa região usa-se:
dens. pop.=
Total de habitantes existentes nessa região
superﬁcie (em km2) dessa região
Exemplo 11.2.1 Se a superfície de um lugar é de 9 milhares de km2
e a população desse
lugar é de 414 milhares de habitantes, a densidade populacional é:
dens. pop. =
414 milhares de habitantes
9 milhares por km2
= 46 habitantes por km2

11.3 Estruturas demográficas
A análise de alguns aspectos globais da população também compreende o conhecimento
das estruturas demográficas.
Uma estrutura demográfica consiste na subdivisão da população em grupos homo-
géneos a partir de determinadas características.
Existem diversos tipos de estruturas: por sexos e idades, por estado civil, por actividade
económica, por níveis de instrução, ...
Exemplo 11.3.1 Analisemos a repartição por sexos e idades:
a) a repartição por sexos justifica-se pelo facto das populações masculina e feminina
desempenharem funções diferentes na sociedade, com incidências demográficas devido
a um complexo de factores biológicos, sociais e culturais.
b) a repartição por idades justifica-se pela necessidade:
• de se analisar os efeitos específicos de cada idade (com o aumento da idade os
comportamentos e as capacidades vão-se modificando)1
;
• de se comparar determinados aspectos das fases da vida (início da socialização,
instrução primária, primeiro casamento,...) em pessoas com diferentes idades2
.
11.3.1 Pirâmides de idades
A pirâmide de idades é uma representação gráfica da distribuição de uma população por
sexos e idades, que permite ter uma visão de conjunto das estruturas de idades de uma
população.
• As idades são representadas num eixo vertical. Os efectivos (população existente) são
representados em dois semi-eixos horizontais; o da esquerda é reservado aos efectivos
masculinos; o da direita aos femininos.
As figuras 11.2 e 11.3 apresentam dois exemplos de pirâmides de idades.
• Podemos construir pirâmides por idades e por grupos de idades.
• Representando os efectivos em números absolutos, a população em cada idade (ou
grupo de idades) é representada por rectângulos, cuja área é proporcional ao efectivo
(a ’largura’ é constante e o ’comprimento’ é proporcional ao efectivo ou volume da
população (número de habitantes)).
1
Efeito idade
2
Efeito geração

Figura 11.2: Exemplo de pirâmide de idade [1]

Figura 11.3: Exemplo de pirâmide de idade [1]

• A escala utilizada deve ser tal que a pirâmide terá uma altura igual (≈) a 2
3
da largura
total.
• Podem aparecer vários tipos de pirâmides, embora a mais vulgar seja a ’triangular’.
Assim, existem as pirâmides com forma de
1. acento circunflexo que é típica dos países não desenvolvidos com mortalidade e
natalidade muito elevadas e caracteriza-se por ter uma base larga e topo muito
reduzido;
2. urna que é típica dos países desenvolvidos com baixos níveis de mortalidade e
natalidade e tem uma base muito reduzida e um topo bastante empolado;
3. ás de espadas, típica dos países desenvolvidos com aumento de fecundidade num
certo período de tempo.
• Quando trabalhamos com grupos de idades, a largura do rectângulo é proporcional
ao número de anos existentes em cada grupo. Se os grupos forem quinquerais (muito
vulgar) basta fixar uma largura, que será constante.
O comprimento é proporcional ao total dos efectivos das diversas idades (que com-
põem o grupo) dividido pelo número de anos do grupo (quinquenal→5).
• Se interessar fazer comparações no tempo ou no espaço, é mais conveniente represen-
tar os efectivos relativos. A comparação passa a ser feita em termos de percentagens
entre os diferentes grupos de idades.
11.3.2 Grupos funcionais
Quando temos que comparar muitas estruturas populacionais, ao longo do tempo, para
verificar a sua evolução, ou comparar estruturas de um número vasto de localidades, surgem
vulgarmente muitos gráficos a partir dos quais é difícil tirar conclusões. Para uma visão
mais rápida da evolução ou da diversidade de estruturas é mais conveniente compactar
a informação disponível, de acordo com determinados critérios. O mais importante é a
idade. É possível concentrar a análise num número reduzido de subgrupos, chamados
grupos funcionais.
Por exemplo, dividir a população em três grandes grupos: 0-14 anos que define a
população jovem, 15-64 anos que define a população activa e 65 e +anos que define a
população velha. Uma outra divisão consiste nos seguintes grupos: 0-19, 20-59 e 60 e +
anos.
É possível ainda pegar num destes grupos e dividi-lo. Por exemplo, o grupo 20-59 pode
dividir-se em 20-39, população activa jovem, e 40-59, população activa velha.
Se o critério para a definição de grupos funcionais for o da escolaridade, teríamos os
seguintes grupos: 0-5 (população em idade pré-escolar), 5-18 (população em idade escolar)
e 18-24 (população em idade universitária).

Deﬁnidos os grupos funcionais deve proceder-se à manipulação dos dados, transformando-
os em índices-resumos que se constroem a partir dos grupos funcionais.
Os índices-resumos mais importantes são:
• percentagem de jovens
população com 0-14 (ou 0-19) anos
população total
× 100%
• percentagem de activos
população com 15-64 (ou 20-59) anos
população total
× 100%
• percentagem de velhos
população com 65 e + (ou 60 e +) anos
população total
× 100%
• índice de vitalidade (’racio’ entre velhos e jovens)
população com 65 e + anos
população com 0-14
× 100%
• ’racio’ de dependência dos jovens
× 100%
• ’racio’ de dependência dos velhos
população com 65 e + anos
× 100%
• ’racio’ de dependência total
população com 0-14 e 65 e + anos
× 100%

Capítulo 12
Qualidade dos dados
12.1 Relação de masculinidade
As pirâmides de idades nunca são simétricas pois nascem mais rapazes do que raparigas.
Por cada 100 raparigas nascem 105 rapazes. No entanto a mortalidade (factor fundamental
na análise da redução dos diversos efectivos) é mais intensa nos homens do que nas mu-
lheres. Factores como as migrações, guerras, ... podem modificar ainda mais a assimetria
’natural’.
A relação de masculinidade é dada pelo quociente, para cada idade (ou grupo de
idades),
efectivos masculinos
efectivos femininos
× 100.
Como a relação de masculinidade dos nascimentos ronda os 105, a relação de masculi-
nidade do primeiro grupo de idades é muito próxima de 105.
À medida que se avança na idade, devido ao facto de que a mortalidade masculina é
superior à mortalidade feminina, as relações de masculinidade diminuem. É o efeito idade.
O índice, relação de masculinidade dos nascimentos, é frequentemente utilizado para
apreciar a qualidade do registo de nascimentos, por sexos. Normalmente existem
omissões mais acentuadas num sexo do que noutro.
Quando o número de nascimentos não é suficientemente grande, alguns desvios podem
ser consequência directa de flutuações aleatórias mesmo estando em presença de observa-
ções perfeitas. No entanto, é possível calcular um intervalo de variação deste erro, em
função do número de nascimentos observados:
1. Para uma relação de masculinidade de 105, em 1000 nascimentos teríamos 512 mas-
culinos e 488 femininos. A proporção de rapazes é de 0.512 = 512
1000
. A proporção de
raparigas é então de 0.488.
2. Os limites do intervalo de confiança a 95% (0.95 de probabilidade de conter o valor)
para a proporção são
60

CAPÍTULO 12. QUALIDADE DOS DADOS 61



0.512 − 1.96
0.512 × 0.488
n
i
,
0.512 + 1.96
0.512 × 0.488
n
s



em que n representa o número total de nascimentos.
3. Os limites de confiança da relação de masculinidade são
i
1 − i
× 100,
s
1 − s
× 100
em que i e s são respectivamente os limites inferior e superior do intervalo do passo
anterior.
4. Se o valor da relação de masculinidade observado está fora do intervalo (do passo
anterior) é de admitir uma má qualidade no registo dos nascimentos. Se for superior
existe provavelmente um sobre-registo dos nascimentos masculinos (menos provável)
ou um sub-registo dos femininos (mais provável).
12.2 Índice de Whipple
O método baseado no cálculo da relação de masculinidade dos nascimentos e, quando o
número de nascimentos é pequeno, do intervalo de variação (limites de confiança da relação
de masculinidade) serve para analisar a qualidade dos dados das estatísticas demográficas.
O método baseado no índice de Whipple serve para analisar determinado tipo de
distorção existente nos recenseamentos.
O tipo de distorção referida é a atracção pelos números (idades) terminados em 0 e 5.
Sabe-se que em demografia e em países não desenvolvidos e há muitos anos atrás as
pessoas tinham dificuldade em declarar com exactidão a sua idade. Por exemplo, pessoas
com 48, 49, 51 e 52 anos de idade tinham a tendência em declarar que tinham 50 anos.
Esta idade aparecia com muitos registos e os valores adjacentes tinham poucos efectivos.
O índice de Whipple constrói-se da seguinte maneira:
1. calcula-se o número de pessoas entre 23 e 62 anos (inclusivé);
2. calcula-se o número de pessoas que, no intervalo de idades de 23 a 62 anos, têm
idades registadas que terminam em 0 e 5;
3. calcula-se o índice
IW =
no
de pessoas na alínea 2 × 5
no
de pessoas na alínea 1
× 100.

O IW pode variar entre 100 (ausência de concentração) e 500 (caso limite em que todas
as pessoas declaram idades terminadas em 0 e 5)
Para facilitar a análise usa-se a escala de valores do anuário demográﬁco das Nações
Unidas de 1963. Assim
se pode concluir-se que
IW < 105 dados muito exactos
105 ≤ IW < 110 dados relativamente exactos
110 ≤ IW < 125 dados aproximados
125 ≤ IW ≤ 175 dados grosseiros
IW > 175 dados muito grosseiros
12.3 Índice de irregularidade
Este índice serve para medir qualquer tipo de atracção, por exemplo, pelos números pares
e impares, pelo número 0, pelo número 5, pelos números terminados em 1,2,3, ...
O índice de irregularidade constrói-se da seguinte forma:
1. calcula-se o número de pessoas com a idade cuja atracção se pretende medir;
2. calcula-se a média aritmética do número de pessoas com as 5 idades que enquadram
a idade que se pretende analisar;
II =
no
de pessoas da alínea 1
no
de pessoas da alínea 2
× 100
Quanto mais o II se afasta de 100 mais demonstra a força da atracção.
12.4 Índice combinado das Nações Unidas
Este índice serve para medir a qualidade global de um recenseamento.
Este índice combina três indicadores:



indicador de regularidade das idades das pessoas do sexo masculino
indicador de regularidade das idades das pessoas do sexo feminino
indicador de masculinidade
O índice combinado das Nações Unidas calcula-se da seguinte maneira:
1. calcula-se o índice de regularidade dos sexos (i.r.s.) da seguinte forma:

i.r.s. = média aritmética das diferenças, em valor absoluto, entre as
relações de masculinidade dos grupos sucessivos
2. calcula-se o índice de regularidade das idades do sexo masculino
(i.r.i.(M)) e do sexo feminino (i.r.i.(F)) da seguinte maneira:
i.r.i.(M) = média aritmética das diferenças, em valor absoluto,
entre as relações de regularidade (r.r.) e o 100
com
r.r.=
efectivos do grupo
média aritmética dos efectivos dos 2 grupos adjacentes
× 100
(com fórmulas idênticas para o i.r.i.(F))
ICNU=3 × (i.r.s.)+i.r.i.(M)+i.r.i(F)
Para faciliar a interpretação existe uma grelha (das Nações Unidas) classificativa:
se pode concluir-se que
ICNU < 20 a validade do recenseamento é boa
20 ≤ ICNU < 40 a qualidade é má
ICNU ≥ 40 a qualidade é muito má
12.5 A equação da concordância
A equação da concordância tem como objectivo verificar se existe ou não uma con-
cordância entre os diversos dados disponíveis. Estes dados estão relacionados com os dois
tipos de movimentos:
natural
migratório
que se verificam num determinado período de tempo.
Considerem-se dois instantes x e x + n (n anos após o instante x), i.e., dois períodos
com n anos de diferença.
Se conhecermos a população nos dois instantes:

Px ← população no momento x
Px+n ← população no momento x + n
e se
N é o número de nascimentos veriﬁcados naquele período,
O, o número de óbitos ocorridos naquele período,
E, o número de emigrantes naquele período,
e I, o número de imigrantes no mesmo período,
então a equação da concordância (se todos os elementos nela intervenientes tiverem sido
correctamente apurados) é:
Px+n = Px + N − O + I − E
em que N − O representa o crescimento natural e I − E representa o crescimento
migratório.
A Px + N − O + I − E chama-se população esperada.
Quando a população esperada não coincide com a população recenseada, Px+n, deve-se
tentar explicar essa diferença. Três hipóteses podem ser formuladas:
1. as parcelas N e I (+) estão subavaliadas;
2. as parcelas O e E (-) estão sobreavaliadas;
3. os recenseamentos não são de boa qualidade.
Face à realidade do país em estudo (na época em estudo) assim se podem tirar as
conclusões mais acertadas.
Algumas recomendações:
1. Face à diferença observada entre população esperada e população recenseada ter em
atenção o sinal dessa diferença;
2. Veriﬁcar a qualidade dos dados pelos índices de irregularidade e Whipple e ICNU e
pela relação de masculinidade dos nascimentos. Se a qualidade for boa, afasta-se a
hipótese de recenseamento de má qualidade.
3. Resta uma análise dos movimentos migratórios;
4. Resta ainda uma análise dos registos de nascimento e dos óbitos.
Nos registos de nascimento, a relação de masculinidade dos nascimentos ajuda a
concluir sobre o subregisto (ou sobreregisto).
5. Notar que é mais frequente um subregisto do que um sobreregisto.

Capítulo 13
Análise da mortalidade
O estudo da mortalidade, enquanto fenómeno social, gira em torno das três vertentes:
1. caracterização do declínio observado na época em estudo;
2. estudo dos factores responsáveis por esse declínio;
3. estudo das diferenças observadas entre determinados grupos (mortalidade diferencial)
13.1 Taxa bruta de mortalidade
A taxa bruta enquanto medida elementar de análise da mortalidade geral é dada por
t.b.m.=
total de óbitos num período
população média existente nesse período
× 1000
t.b.m. signiﬁca taxa bruta de mortalidade.
A taxa bruta de mortalidade pode ser calculada como resultante da interacção entre o
modelo do fenómeno e a estrutura por idades.
A t.b.m. é a soma dos produtos das estruturas relativas em cada idade (ou grupo de
idades) pelas taxas nessas idades (ou grupo de idades):
x=0
Pxtx
em que Px representa a estrutura relativa em cada grupo de idades (proporção) e é igual a
população do grupo de idades
população total
e tx é a taxa de mortalidade do grupo que é igual a
total de óbitos no grupo
população no grupo
× 1000.
Ao conjunto de taxas por idades (ou grupo de idades) chama-se modelo do fenómeno.
65

CAPÍTULO 13. ANÁLISE DA MORTALIDADE 66
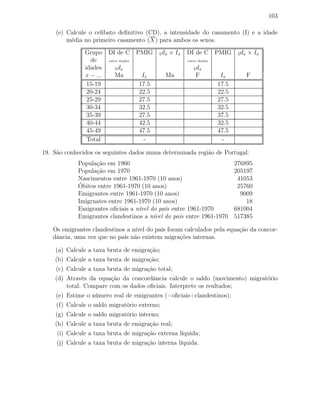
Exemplo 13.1.1 [3] Completar e
Grupos de idades total de óbitos população tx × 1000 Px Pxtx
1 1848 46514 39,73 0,0326 1,30
1-4 1087 184916 5,88 0,1295 0,76
5-9 318 215461 1,48 0,1509 0,22
10-14 171 173563 0,99 0,1215 0,12
15-19 198 145227 1,36 0,1017 0,14
20-24 197 125339 1,57 0,0878 0,14
25-29 185 101699
30-34 182 82518
35-39 200 73395
40-44 247 60945
45-49 251 53330
50-54 346 46561
55-59 398 37816
60-64 483 27889
65-69 502 20397
70+ 2463 32502
Total 9076 1428082 1,0000 6,37
• calcular a taxa bruta de mortalidade (geral);
• calcular a taxa bruta de mortalidade como resultante da interacção entre modelo e
estrutura.
Por este processo ficam visíveis os factores intervenientes - o modelo e as estruturas.
Quando surgem diferenças nos valores da t.b.m., elas podem vir dos tx (modelos) ou
dos Px (estruturas) e têm significados diferentes:
• Variações entre modelos (tx) significam a existência de diferentes riscos de mortali-
dade (diferenças nas condições gerais de saúde e higiene);
• Variações entre estruturas (Px; maior ou menor envelhecimento) são alheias ao fenó-
meno em análise.
As taxas brutas são muito sensíveis aos efeitos da estrutura. Basta as proporções da
população serem diferentes nos grupos em que a mortalidade é mais intensa para termos
importantes efeitos de estrutura que nos impossibilitam a comparação entre países, regiões
ou épocas.
A validade de uma análise feita através das taxas brutas é tanto menor quanto mais di-
versificadas forem as estruturas das regiões ou épocas que se querem comparar. A validade
aumenta com a homogeneização das estruturas populacionais.

13.2 Tipos particulares de mortalidade
1. A taxa de mortalidade por idades e por grupos de idades é dada por
total de óbitos entre as idades exactas
população média existente entre essas idades
× 1000
2. A taxa de mortalidade infantil (t.m.i) calcula-se da seguinte maneira:
total de óbitos entre 0 e 1 anos exactos
população média existente entre 0 e 1 anos exactos
× 1000
Exemplo 13.2.1 Se numa região houve 11751 nascimentos em 1961, 11730 em
1962, 385 óbitos com menos de 1 ano de vida em 1962, então a t.m.i. em 1962 é:
t.m.i. =
385
11740.5
× 1000 = 32.8 por mil
3. A taxa de mortalidade infantil clássica (t.m.i.c.) é dada por
total de óbitos com menos de 1 ano
total de nascimentos nesse ano
× 1000.
Tradicionalmente esta medida da taxa de mortalidade infantil relacionava o número
de óbitos com menos de um ano e o efectivo dos nascimentos nesse ano (noção de
quociente - proporção).
Exemplo 13.2.2 Tomando os valores do exemplo 13.2.1:
t.m.i.c.=
385
11730
× 1000 = 32.8 por mil
Esta deﬁnição não é totalmente satisfatória pois os óbitos ocorridos num ano não
resultam apenas de nascimentos desse ano. Sem informação relativa ao ano de nas-
cimento do óbito ocorrido num certo ano, podemos imputar os óbitos a uma média
ponderada dos dois efectivos de nascimentos em causa (do ano em questão e do ante-
rior). Este novo processo para calcular a mortalidade infantil chama-se método da
média ponderada (m.m.p.).
Os coeﬁcientes de ponderação que se devem usar são os da tabela:

Ponderação da mortalidade infantil
(método de Shryock e Siegel)
t.m.i.c. k k
200 0.6 0.4
150 0.67 0.33
100 0.75 0.25
50 0.8 0.2
25 0.85 0.15
15 0.95 0.05
Os coeficientes de ponderação a usar têm em conta os seis tipos de população, de
acordo com o nível de mortalidade infantil esperado e que é determinado pela taxa
de mortalidade infantil clássica. Assim
t.m.i.(m.m.p.)=
total de óbitos com menos de 1 ano
k N0 + k N1
× 1000
sendo N0 o total de nascimentos do ano anterior, N1 o total de nascimentos daquele
ano e k e k os coeficientes da tabela que correspondem à t.m.i.c. calculada.
Exemplo 13.2.3 Do exemplo 13.2.1:
t.m.i.(m.m.p.) =
385
0.15(11751) + 0.85(11730)
× 1000 = 32.8 por mil
uma vez que a t.m.i.c.=32.8 e da tabela, o valor mais próximo, corresponde à 2a
linha
a contar do fim.
4. Taxas de mortalidade endógena e exógena
As causas que originam a mortalidade infantil são endógenas e exógenas.
As endógenas são consequência de deformações congénitas, doenças hereditárias ou
traumatismos causados pelo parto. Estes óbitos ocorrem normalmente durante o
primeiro mês (menos de 28 dias).
Os óbitos exógenos estão relacionados com doenças infecciosas, alimentação e cuida-
dos hospitalares insuficientes ou acidentes. Estes óbitos ocorrem nos restantes meses
(de 28 dias até 11 meses).
Não havendo registo de óbitos por causas de morte pode usar-se um método (J.
Bourgeois-Pichat) que não exige senão o conhecimento dos óbitos por dias e idades.
Assim, para se calcular o total de óbitos exógenos, soma-se ao total de óbitos
observados no intervalo 28-365 dias, 22.8% destes (ou 25% para uma divisão de 31 a

365 dias). O total de óbitos endógenos é então a diferença entre o total dos óbitos
registados e os óbitos exógenos calculados.
A taxa de mortalidade infantil clássica é igual à taxa de mortalidade endógena
(t.m.end.) mais a taxa de mortalidade exógena (t.m.exo.) sendo
t.m.end.=
total de óbitos endógenos
total de nascimentos do ano
× 1000
t.m.exo.=
total de óbitos exógenos
total de nascimentos do ano
× 1000.
13.3 Tábua de mortalidade
É possível fazer uma análise da mortalidade de uma população calculando outros índices.
O princípio da estandardização [3], que separa o impacte das estruturas do das frequências
(modelos), tem como objectivo manter o efeito das estruturas constante, calculando os
índices comparativos. Não é contudo o método mais usado.
É comum usar o princípio da translação. Com este princípio procura-se estimar a inten-
sidade e o calendário a partir das frequências calculadas em transversal. Aplica-se, assim,
o método da coorte ﬁctícia que consiste em transpôr os fenómenos que se observam num
determinado momento do tempo, para uma coorte imaginária. No caso da mortalidade, a
intensidade mede o número médio de acontecimentos por pessoa e o calendário mede a
sua repartição no tempo. O calendário, ao ser resumido pelo índice da tendência central,
a média, dá-nos a possibilidade de conhecer a duração de vida média das pessoas.
No cômputo dos efectivos de uma população podem surgir efectivos de idade ignorada.
Havendo um número signiﬁcativo de pessoas de idade ignorada, pode usar-se um critério
de repartição dessas pessoas. Calcula-se o factor (Coale e Demeny) de correcção:
população total
população total - população de idade desconhecida
e os efectivos de cada idade (ou grupo de idades) são multiplicados por este factor.
Existem tábuas de mortalidade por idades que se chamam completas, e tábuas de
mortalidade por grupos de idades, chamadas tábuas abreviadas.
Nota 13.3.1 No caso da tábua de mortalidade abreviada, as diversas funções são calcu-
ladas por grupos de idades quinquenais (n=5), excepto no primeiro grupo, que devido à
importância da mortalidade infantil, se divide em dois grupos:
• menos de 1 ano (n=1)
• 1-4 anos completos (n=4).
As diversas funções que integram uma tábua de mortalidade são:

1. Taxa de mortalidade entre a idade exacta x e a idade exacta x + n:
nmx =
total de óbitos com idade entre x e x + n
habitantes com idade entre x e x + n
2. Quociente de mortalidade que é equivalente à probabilidade de morrer entre a
idade (exacta) x e a idade (exacta) x + n:
nqx =
2n nmx
2 + n nmx
.
Os casos mais usados são:
• n = 1
1qx =
2 1mx
2 + 1mx
• n = 4
4qx =
8 4mx
2 + 4 4mx
• n = 5
5qx =
10 5mx
2 + 5 5mx
Nota 13.3.2 1q0 é a taxa de mortalidade infantil e nqx do último grupo de idades
=1 (todas as pessoas terão de desaparecer)
3. Probabilidade de sobrevivência entre as idades (exactas) x e x + n:
npx = 1 −n qx
Nota 13.3.3 No último grupo de idades npx = 0 (ninguém irá sobreviver)
4. Sobreviventes em cada idade exacta x:
Para tornar possível as comparações temporais e espaciais, aplica-se a um mesmo
efectivo à nascença - a raiz da tábua, s0 = 100000 - a lei da mortalidade de-
ﬁnida pelos nqx (quociente de mortalidade) ou da sobrevivência deﬁnida pelos npx
(probabilidade de sobrevivência).
Os sobreviventes em cada idade x + n:

sx+n = sx npx
ou
sx+n = sx(1 −n qx) = sx − sx nqx
5. Distribuição dos óbitos (tendo em conta o efectivo inicial de 100000) por idades
ou grupos de idade
ndx = sx − sx+n
ou
ndx = sx nqx
6. Número de anos vividos pelos sobreviventes sx entre as idades x e x + n:
[O número de anos vividos obtém-se multiplicando a média dos efectivos entre idades
exactas pelo número de anos]
(a) numa tábua de mortalidade completa
Nx =
1
2
(sx + sx+1)
(b) numa tábua de mortalidade abreviada
nNx =
n
2
(sx + sx+n)
Nota 13.3.4 Devido à não linearidade da função de sobrevivência nos primeiros
anos de vida, é mais conveniente (aproximação mais exacta) usar:
1N0 = k s0 + k s1
4N1 = 4 k s1 + k s5
em que k e k são os coeﬁcientes de ponderação usados no cálculo da mortalidade
infantil (pelo método das médias ponderadas), em 13.2.
Nota 13.3.5 Para o último grupo (70 e + anos) tem-se:
Nk+ = Tk ↔ N70+ = T70+ (ver nota 13.3.8)
7. Probabilidade de sobrevivência entre dois anos completos ou entre dois grupos
de anos completos:

(a) numa tábua de mortalidade completa
Px =
Nx+1
Nx
nPx =
nNx+n
nNx
Nota 13.3.6 No primeiro grupo de idades, tem-se
P0 =
5N0
5s0
=
1N0 +4 N1
500000
5P1 =
5N5
1N0 +4 N1
.
Nota 13.3.7 O último nPx calcula-se dividindo o último Tx pelo penúltimo (ver nota
13.3.8).
8. Total de anos vividos pela coorte depois da idade x:
Como nNx é o número de anos vividos entre as idades x e x + n, o total de anos
vividos pela coorte obtém-se somando os nNx. Assim,
(a) numa tábua de mortalidade completa:
Tx =
w
x
Nx
Tx =
w
x
nNx.
Nota 13.3.8 O último Tx (ou Tk), que é igual a Nk+,é:
Tk =
sk
mk+
com mk+ a mortalidade do último grupo de idades.

9. Esperança de vida na idade x, i.e., o número médio de anos que resta para viver
às pessoas que atingiram a idade x.
Quando x = 0, é a esperança de vida à nascença (é o número total de anos vividos
desde o nascimento dividido pelo efectivo inicial)
e0 =
T0
s0
,
ou seja, o número médio de anos vividos desde o nascimento (ou o calendário). Do
mesmo modo,
ex =
Tx
sx
.
.

Capítulo 14
Análise da natalidade e da fecundidade
A característica principal da natalidade no século XX é o declínio (embora posterior ao da
mortalidade).
Em muitos países não desenvolvidos esse declínio ainda não começou ou está no início.
Existe uma grande diversidade de situações no tempo e no espaço.
Os estudos sobre a natalidade giram à volta de três eixos fundamentais:
1. caracterização do declínio observado na época contemporânea;
2. estudo dos factores responsáveis por esse declínio;
3. estudo das diferenças observadas entre determinados grupos.
Relativamente à caracterização do declínio, passou-se de valores entre os 30 por mil e os
40 por mil, no início do século, para os 10 por mil ou 15 por mil, nos países desenvolvidos.
A diversidade de situações é maior na natalidade do que na mortalidade. Esta diversidade
levou à procura das causas do declínio da natalidade. Algumas dessas causas são: factores
biológicos, relações sexuais, leis e costumes, divórcios, viuvez e abstinência, contracepção e
aborto, que por sua vez estão dependentes de diversos factores económios, sociais e culturais
(demograﬁa histórica e social).
As taxas brutas como medidas elementares da análise da natalidade e fecundidade são
as seguintes:
1. a taxa bruta de natalidade:
t.b.n.=
total de nascimentos num período
população média existente no mesmo período
× 1000.
O período usado é normalmente de um ano.
Embora seja um instrumento de análise muito grosseiro (que isola os efeitos de
estrutura) é possível introduzir uma correcção. Esta correcção relaciona os nasci-
mentos directamente com a parte da população onde eles ocorrem, ou seja, com a
população feminina no período fértil (por convenção, dos 15 aos 50 anos). Assim,
74

CAPÍTULO 14. ANÁLISE DA NATALIDADE E DA FECUNDIDADE 75
2. taxa de fecundidade geral:
t.f.g.=
total de nascimentos num período
população feminina no período fértil no mesmo período
× 1000
3. taxa de fecundidade geral como resultante da interacção entre o modelo do fenómeno
e a estrutura por idades.
É possivel decompor a t.b.n. nos seus elementos constitutivos, mas como não ocorrem
nascimentos em todos os grupos populacionais, é mais interessante analisar a t.f.g.
A t.f.g. é a soma dos produtos das estruturas relativas em cada idade (ou grupo de
idades), do período fértil das mulheres, pelas taxas nessas mesmas idades (ou grupo
de idades),
t.f.g.=
50
x=15
pxtx
com
px =
população feminina do grupo de idades
população feminina do período fértil
e
tx =
total de nascimentos no grupo de idades
população feminina no grupo
× 1000
Apesar das diferenças existentes entre as curvas de fecundidade dos diversos países,
estas têm um modelo único: partem do 0 no grupo 0-15 anos; a partir dos 15 anos a
fecundidade é crescente até atingir um máximo entre os 20 e os 30 anos; a partir deste
máximo a fecundidade diminui até atingir de novo 0 por volta dos 50 anos.
Tipos particulares de natalidade e de fecundidade:
1. A fecundidade por idades ou por grupos de idades:
Como os nascimentos ocorrem numa determinada parte da população, não é vulgar
calcular taxas de natalidades por idades ou grupos, mas sim taxas de fecundidade
por idades ou grupos.
2. A fecundidade legítima
Relaciona os nascimentos legítimos com as mulheres casadas no período fértil.
t.f.l.=
total de nascimentos legítimos
mulheres casadas 15-49 anos
× 1000
A fecundidade legítima também pode ser medida por idades ou por grupos de idades.
Neste caso aplicam-se as regras já referidas nos casos anteriores.

3. A fecundidade ilegítima
Relaciona os nascimentos ilegítimos com as mulheres não casadas no período fértil
t.f.i.=
total de nascimentos ilegítimos
mulheres não casadas 15-49 anos
× 1000
4. Descendência média
O fenómeno em análise é a intensidade da fecundidade e é dada por
d.m.=amplitude do intervalo ×
49
x=15
taxas de fecundidade geral
em que as taxas de fecundidade geral são calculadas por idades ou grupos de idades.
5. Taxa bruta de reprodução
Esta correponde à descendência média feminina por mulher na ausência de mortali-
dade e calcula-se a partir de:
t.b.r.=descendência média × 0.488
em que o valor 0.488 resulta da aplicação da relação de masculinidade no nascimento:
100
100+105
.
6. Taxa líquida de reprodução
Esta taxa tem em conta a mortalidade. Assim, multiplicando a amplitude do inter-
valo por 0.488 e pelo somatório dos produtos das taxas de fecundidade geral pelas
probabilidades de sobrevivência (npx = sx+n
sx
)(por idades ou grupos de idades), obtém-
se
t.l.r.=amplitude do intervalo × 0.488 ×
49
x=15
t.f.g. npx
7. Idade média da fecundidade
É a idade média da população feminina no período fértil considerando a taxa de
fecundidade geral como ’frequência relativa’ de cada grupo de idades:
MI =
49
x=15 t.f.g.Ix
49
x=15 t.f.g.
.
Os somatórios são relativos aos 7 grupos de idades de amplitudes iguais a 5, do
período fértil, se as taxas de fecundidade geral forem calculadas por grupos de idade.
A taxa de fecundidade geral de cada grupo de idades, t.f.g., é dada por

t.f.g. =
total de nascimentos no grupo x
população feminina (no período fértil) no grupo x
.
O Ix é o ponto médio, do grupo x, das idades. Por exemplo, no grupo 15-19, I15 =
17.5; no grupo 20-24, I20 = 22.5; no grupo 25-29, I25 = 27.5; no grupo 30-34,
I30 = 32.5; no grupo 35-39, I35 = 37.5; no grupo 40-44, I40 = 42.5; e no grupo 45-49,
I45 = 47.5.
Nota 14.0.9 O valor de MI de referência no mundo varia entre os 26 e 33 anos.
8. Variância da fecundidade
σ2
=
49
x=15 t.f.g.(Ix − MI)2
49
x=15 t.f.g.
e o desvio padrão σ é
√
σ2.
Nota 14.0.10 Um valor baixo de MI pode ser consequência de um casamento pre-
coce. Observando a curva das proporções de mulheres casadas, poder-se-á concluir se
se trata de casamento precoce ou se o valor baixo é devido à contracepção (curva de
fecundidade geral desce rapidamente depois de uma certa idade).
Exemplo 14.0.1 No exemplo da ﬁgura 14.1, o casamento é relativamente tardio.
Um casamento tardio associado à contracepção origina uma variância baixa. As duas
curvas foram ajustadas a 100. As colunas 3 e 5 da tabela da ﬁgura 14.2 apresentam
os valores já ajustados.

C urvas de proporções de m ulheres casadas e
fecundidade
0
50
100
15-19 20-24 25-29 30-34 35-39 40-44 45-49
Casadas Fecundidade
Figura 14.1: Gráﬁco das curvas
Grupo de taxa de ajuste a proporção ajuste a
idades fecundidade 100 de mulheres 100
geral casadas
15-19 0.02197 12 0.0406 5
20-24 0.16807 93 0.4739 55
25-29 0.18008 100 0.7891 92
30-34 0.10730 60 0.8511 100
35-39 0.05341 30 0.8550 100
40-44 0.01880 10 0.8359 98
45-49 0.00119 1 0.7973 90
Figura 14.2: Tabela das taxas de fecundidade geral [3]

Capítulo 15
Análise da nupcialidade
A nupcialidade não é considerada uma variável microdemográfica autêntica, uma vez que a
sua variação - aumento ou diminuição - não afecta directamente a dinâmica populacional.
Intervém na dinâmica populacional através da natalidade.
Muitos autores consideram a nupcialidade como um aspecto particular do estudo da
natalidade.
A evolução verificada, a partir do fim da segunda guerra mundial, na nupcialidade
dos países desenvolvidos é caracterizada por uma diminuição das taxas brutas e por um
aumento do divórcio.
15.1 Taxas de nupcialidade
As taxas brutas enquanto medidas elementares de análise são as seguintes:
1. Taxa bruta de nupcialidade
Esta taxa mede o nível de nupcialidade e é dada por
t.b.nup.=
total de casamentos observados num período
população média desse período
× 1000
O período normalmente usado é de um ano.
A taxa bruta de nupcialidade também pode ser considerada (tal como a mortalidade
e a natalidade) como o resultado da interacção entre o modelo do fenómeno e a estru-
tura por idades. No entanto, aqui haveria que distinguir entre primeiro casamento,
segundo casamento, casamento de solteiros, de viúvos e divorciados... A análise seria
muito complexa!
Tomemos em consideração apenas o seguinte:
(a) o modelo da nupcialidade é muito semlhante ao da fecundidade - parte de 0 por
volta dos 15 anos, atinge um máximo por volta dos 30 anos e diminui a partir
daí.
79

CAPÍTULO 15. ANÁLISE DA NUPCIALIDADE 80
A grande diferença em relação à fecundidade é que não se reduz a 0 por volta
dos 50 anos.
(b) utilizando a lógica das taxas é possível calcular outros indicadores mais soﬁsti-
cados.
2. Taxa de nupcialidade geral
Esta taxa de nupcialidade geral relaciona os casamentos com as pessoas ”casáveis” e
é dada por
t.n.g.=
número de casamentos
população com + de 15 anos
× 1000.
3. Taxa de nupcialidade geral dos solteiros
Esta taxa relaciona os casamentos com as pessoas ”casáveis”, excluindo os viúvos e
divorciados.
Nota 15.1.1 Pode ser calculada por sexos.
4. Taxas de nupcialidade por idades ou grupo de idades, e por sexos.
Nota 15.1.2 Relaciona o casamento numa determinada idade (ou grupo de idades)
com a população dessa idade (ou desse grupo de idades).
Exemplo 15.1.1 A taxa de nupcialidade do sexo masculino no grupo 25-29 é:
t.n.grupo(masc.)=
número de casamentos (25-29) masc.
população (25-29) masc.
× 1000.
5. Taxa de nupcialidade por ordem
Tem em conta a ordem do casamento. Assim,
(a) Taxa do primeiro casamento
t.p.c.=
número de casamentos de ordem 1
solteiros com + de 15 anos
× 1000
Nota 15.1.3 É vulgar calcular esta taxa por grupos de idades e sexos separados.
Exemplo 15.1.2 A taxa do primeiro casamento no grupo 20-24 é
número de casamentos de ordem 1 no grupo 20-24
solteiros no grupo 20-24
× 1000;

(b) Taxa do segundo casamento
t.s.c.=
número de casamentos de ordem 2
viúvos + divorciados
× 1000.
6. Taxa bruta de divórcio
Esta taxa relaciona o número de divórcios com o total da população,
t.b.div.=
número de divórcios
total da população
× 1000
(a) Taxa de divórcio geral
t.d.geral=
população com + 15 anos
× 1000
Nota 15.1.4 É vulgar calcular esta taxa por sexos.
(b) Taxa de divórcio dos casados
t.d.casados=
população casada
× 1000
(c) Taxa de divórcio por idades ou grupo de idades
Exemplo 15.1.3 A taxa de divórcio do grupo de 20-24 é
t.d.(20-24)=
número de divórcios no grupo 20-24
população no grupo 20-24
× 1000
(d) Taxa de divórcio por duração de casamento
Exemplo 15.1.4 A taxa de divórcio com 10 anos de duração é dada por
t.d.(10 anos)=
número de divórcios com 10 anos
população casada há 10 anos
× 1000
7. Taxa bruta de viuvez
Esta taxa relaciona o número de viúvos com o total da população e é dada por
t.b.viuvez=
número de viúvos
população
× 1000.

15.2 Tábua de nupcialidade
A partir de uma tábua de nupcialidade, é possível estimar a intensidade e o calendário do
fenómeno em análise.
Para a construir teremos de ter informação relativa aos casamentos por grupos de idades
e às estruturas populacionais por estado civil.
Raciocinando em termos do primeiro casamento e aplicando o princípio da coorte fictí-
cia, tudo se passa como na mortalidade, em que imaginamos uma geração que ao percorrer
as idades da vida, é submetida em cada idade às condições reais de mortalidade observadas
num determinado momento.
No caso do fenómeno da nupcialidade, temos uma geração de solteiros que a partir dos
15 anos (idade minimamente significativa) e até aos 50 anos (idade a partir da qual o
primeiro casamento é estatisticamente pouco relevante) irá ser ’submetida’ ao casamento.
Assim,
• os óbitos de uma tábua de mortalidade passam a ser os primeiros casamentos de uma
tábua de nupcialidade;
• os sobreviventes de uma tábua de mortalidade passam a ser os celibatários de uma
tábua de nupcialidade.
Nota 15.2.1 A diferença principal reside no facto de que na mortalidade, no fim da ge-
ração ninguém sobrevive (intensidade =1), enquanto que no caso da nupcialidade existem
sempre ’sobreviventes’ ao casamento e que são os celibatários definitivos.
Temos, assim:
5nx = taxa de nupcialidade dos solteiros por grupos de
idades quinquenais;
5qx = probabilidade do ’primeiro casamento’ quinquenal
com
5qx =
10 5nx
2 + 5 5nx
;
5px = probabilidade de sobreviver ao primeiro casamento
com
5px = 1 − 5qx
ou
5px =
Cx+5
Cx
,
em que Cx são os celibatários na idade x e Cx+5 os celibatários na idade x + 5;
5dx = (distribuição de) casamentos entre idades exactas

com
5dx = Cx 5qx
ou
5dx = Cx − Cx+5;
Cx = (sobreviventes) celibatários na idade exacta x
com
Cx+n = Cx − ndx
= Cx − Cx nqx
= Cx(1 −n qx)
Cx+n = Cx npx
e
C15 = 100000.
A intensidade I é dada por
I =
C15 − C50
C15
= 1 −
C50
C15
e I × 100% é a percentagem da população que casa entre os 15 e os 50 anos.
O celibato definitivo é dado por:
CD =
C50
C15
ou
CD = 1 − I
e CD × 100% é a percentagem da população que fica celibatária.
A idade média, X, no primeiro casamento:
X =
I15 5d15 + I20 5d20 + I25 5d25 + ... + I45 5d45
5d15 + 5d20 + 5d25 + ... + 5d45
com I15 = 17.5, I20 = 22.5, ..., I45 = 47.5
Quando não existe informação relativa ao estado civil, é possível estimar a idade média
no primeiro casamento, X, a intensidade, I, e o celibato definitivo, CD, utilizando apenas
as estruturas da população - só será preciso o estado civil das pessoas, por sexos e grupos
de idades. Assim,

1. o celibato deﬁnitivo é estimado por:
CD = T50 =
5T45 +5 T50
2
em que 5Tx é a proporção de celibatários no grupo x - x + 5;
2. a intensidade é estimada por:
I = 1 − T50;
3. A idade média no casamento é estimada por:
X = 15 +
5 45
x=15 5Tx − 35 T50
1 − T50
em que o somatório é calculado de grupo em grupo.

Capítulo 16
Análise dos movimentos migratórios
Além dos movimentos naturais existem outros movimentos de natureza diferente, conheci-
dos por movimentos migratórios e que abrangem as três situações seguintes:



a emigração
a imigração
as migrações internas
A variação destes movimentos no tempo e no espaço depende de factores socio-económicos
complexos internos e externos.
Existem métodos directos e indirectos para analisar os movimentos migratórios.
16.1 Métodos directos de análise
Os métodos directos são aqueles que utilizam directamente os dados disponíveis e são
baseados no cálculo das seguintes taxas:
1. Taxa bruta de emigração:
t.b.emig.=
número de emigrantes oficiais
população
× 1000;
2. Taxa bruta de imigração:
t.b.imig.=
número de imigrantes oficiais
população
× 1000;
3. Taxa bruta de migração total:
t.b.mig.total=
emigrantes oficiais + imigrantes oficiais
população
× 1000.
O cálculo destas taxas é baseado normalmente no período de um ano. A população
refere-se à população média num determinado período (ano).
85

CAPÍTULO 16. ANÁLISE DOS MOVIMENTOS MIGRATÓRIOS 86
16.2 Métodos indirectos de análise
Os métodos indirectos são baseados na equação da concordância (ver no Capítulo 12 sobre
a Qualidade dos dados).
Só através da equação de concordância é possível conhecer valores (aproximados) das
migrações internas e da emigração clandestina. Como
Px+n = Px + N − O + I − E,
tem-se
Px+n − Px = N − O + I − E
onde o Px+n − Px representa o crescimento entre recenseamentos, N − O o cresci-
mentos natural e I − E o crescimentos (saldo) migratório total.
Assim,
crescimento migratório total = crescimento entre recenseamentos –
- crescimento natural.
Nota 16.2.1 Quando o movimento (crescimento) migratório total é muito superior (em
termos absolutos) ao valor obtido pela diferença (imigrantes oficiais - emigrantes oficiais)
estamos perante valores elevados de migração interna e clandestinidade.
Para estimar o peso da clandestinidade é usual usar uma ponderação (que se aplica às
diversas regiões num determinado período) que se calcula a nível do país, num determinado
período. O período normalmente considerado é de 10 anos. O peso da clandestinidade varia
mais no tempo do que no espaço. Assim,
ponderação (a nível do país)=
emigrantes clandestinos num período
emigrantes oficiais no mesmo período
Calcula-se então o número de emigrantes clandestinos multiplicando o número de emi-
grantes oficiais pela ponderação.
O número real de emigrantes é:
n.r.emig. = número de emigrantes oficiais + número de emigrantes
clandestinos.
Finalmente, o saldo migratório interno é:
s.m.inter.=saldo migratório total - saldo migratório externo
em que o saldo migratório total é obtido pela equação da concordância, e o saldo migra-
tório externo pode ser visto como o número de imigrantes oficiais menos o número real
de emigrantes.
A partir do número real de emigrantes calcula-se

CAPÍTULO 16. ANÁLISE DOS MOVIMENTOS MIGRATÓRIOS 87
i) a taxa bruta de emigração real
t.b.emig.(real)=
número real de emigrantes
população
× 1000
ii) a taxa bruta de migração externa líquida
t.b.mig.ext.liq.=t.b.imig. - t.b.emi.(real)
com
t.b.imig. =
número de imigrantes oﬁciais
população
× 1000
iii) a taxa bruta de migração interna líquida
t.b.mig.int.liq.=
saldo migratório interno
população
× 1000
iv) a taxa bruta de migração total líquida
t.b.mig.total liq.=t.b.mig.ext.liq. - t.b.mig.int.liq

89
Abreviações
Ao longo dos próximos exercícios foram usadas as seguintes abreviações:
GI Grupo de Idades
EM Efectivos Masculinos
EF Efectivos Femininos
CF Casados Femininos
FM Falecidos Masculinos
FF Falecidos Femininos
NM Nascimentos Masculinos
NF Nascimentos Femininos
IME Idade Média dos Efectivos
N Nascimentos
O Óbitos
I Imigrantes
Ef Efectivos
Id Idade
P População
V Vivos
M Mortalidade
PMIG Ponto Médio da Idade dos Grupos
C Casamentos
R Recenseamentos
NU Nupcialidade
Prob Probabilidade
DI Distribuição
F Femininos
Ma Masculinos
Prop Proporções
r.m. Relação de Masculinidade
r.r. Relação de Regularidade

90
1. A ﬁgura que se segue representa um mapa da freguesia do Forno da cidade de Âncora.
Use a tabela de números aleatórios para seleccionar uma amostra aleatória de 10 blo-
cos habitacionais desta freguesia. (Nota: cada bloco tem um número de identiﬁcação
no mapa).

91
2. A seguinte tabela apresenta o número de casamentos ocorridos numa dada freguesia,
ao longo de cinco anos
1900 1901 1902 1903 1904
Jan 64 64 62 66 54
Fev 62 70 65 72 68
Mar 50 51 45 50 41
Abr 54 50 48 45 40
Mai 84 82 80 89 75
Jun 90 85 95 84 80
Jul 42 40 38 35 40
Ago 35 30 31 32 40
Set 30 25 35 30 25
Out 71 75 80 70 71
Nov 75 80 71 75 70
Dez 40 42 45 40 35
Calcule os índices sazonais pelo método das médias mensais. Interprete o resultado.
3. Os nascimentos registados numa freguesia de Trás-os-Montes, ao longo de quatro
anos consecutivos foram os seguintes:
1990 1991 1992 1993
Janeiro 7 8 6 7
Fevereiro 17 15 17 14
Março 11 10 12 10
Abril 10 9 8 7
Maio 19 20 17 15
Junho 15 12 11 10
Julho 8 6 6 5
Agosto 5 5 4 5
Setembro 6 7 7 5
Outubro 6 6 7 7
Novembro 7 8 7 8
Dezembro 8 7 9 9
Calcule os índices sazonais e interprete o movimento sazonal nos anos de 1990 a 1993.
4. Foram registados os valores das taxas brutas de mortalidade infantil de uma freguesia

92
ao longo de vinte décadas (1800 a 1990):
1800-09 72 1850-59 41 1900-09 52 1950-59 45
1810-19 77 1860-69 54 1910-19 46 1960-69 15
1820-29 71 1870-79 47 1920-29 55 1970-79 11
1830-39 59 1880-89 50 1930-39 47 1980-89 9
1840-49 62 1890-99 67 1940-49 40 1990-97 5
Estudar a tendência, usando o método das médias móveis baseado num período de
cinco décadas.
5. As taxas brutas de mortalidade infantil masculina ao longo de seis décadas (1770 a
1820) de uma região do Alentejo são as seguintes:
1770-79 1780-89 1790-99 1800-09 1810-19 1820-29
73 81 75 61 70 35
Estudar a tendência usando o método analítico.
Qual terá sido a taxa de mortalidade infantil masculina na década de 1760-1769?
6. Em meados do século XX, foram registados os seguintes valores da região da cidade
de Marinhas:
Freguesias Maró S. Pedro Luz Nora Cruz Velha
EM 31 40 35 51 36
EF 45 51 41 42 52
NM 7 8 7 10 9
NF 7 6 8 8 9
IME 30 31 33 31 35
(a) Calcule a idade média dos habitantes da cidade
(b) Calcule a relação de masculinidade dos habitantes da cidade
(c) Calcule a relação de masculinidade dos nascimentos. Aprecie a qualidade do
registo dos nascimentos, calculando o intervalo (de variação) de conﬁança a
95% de probabilidade.

93
7. Numa freguesia da Beira Alta foram registados, em 1910, os seguintes efectivos
GI EM EF CF FM FF
0 91 95 5 3
1-4 64 67 1 1
5-9 57 59 1 1
10-14 54 56 0 1
15-19 40 44 8 0 0
20-24 39 42 35 2 0
25-29 38 44 36 1 1
30-34 46 40 38 1 0
35-39 34 37 33 0 0
40-44 23 34 29 1 1
45-49 22 39 30 1 0
50-54 19 29 23 0 0
55-59 9 17 12 0 0
60-64 8 15 10 1 0
65-69 7 12 9 1 0
70-74 5 9 5 0 1
75-79 3 6 3 0 1
80-84 2 3 1 1 0
85-89 1 1 0 1 0
(a) Calcular a percentagem de mulheres não casadas com 40 ou mais anos.
(b) Comparar a percentagem da alínea anterior com a percentagem de mulheres não
casadas da freguesia.
(c) Calcular a mediana das idades dos efectivos da freguesia. Interpretar.
(d) Calcular a média das idades de todos os efectivos.
(e) Qual é o tipo da distribuição das idades, relativamente à sua simetria?
(f) Calcule a taxa de crescimento da população da freguesia, pressupondo um cres-
cimento contínuo e sabendo que em 1990 havia 1553 efectivos.
(g) Considerando a mesma taxa da alínea anterior qual terá sido a população da
freguesia em 1810.
(h) Considerando, agora, os seguintes grupos funcionais 0-14, 15-64 e 65 e + anos,
calcule a percentagem de activos do sexo masculino da freguesia em 1910 e o
índice de vitalidade masculina.
(i) Considerando os mesmos grupos da alínea anterior calcule o racio de depen-
dência total dos efectivos do sexo masculino e o ratio de dependência total dos
efectivos do sexo feminino. Interprete.

94
(j) Calcule a taxa bruta de mortalidade geral.
(k) Calcule a taxa bruta de mortalidade como resultante da interacção entre o mo-
delo e a estrutura.
(l) Aprecie a qualidade dos dados, calculando o índice combinado das Nações Uni-
das.
(m) Calcule a taxa de mortalidade infantil clássica.
(n) Do total de óbitos com menos de um ano, 4 ocorreram antes dos 28 dias. Calcule
as taxas de mortalidade infantil endógena e exógena.
(o) Calcule a taxa de fecundidade geral.
8. A população de um distrito era em 1900 de 723012 habitantes. Em 1990 foram
recenseados 731050 habitantes. Qual é a taxa de crescimento verificada neste período
de 90 anos, supondo um crescimento geométrico?
Supondo que o ritmo de crescimento verificado no século XIX foi igual ao do século
XX, qual teria sido a populaçao em 1850?
9. Observe os seguintes dados respeitantes aos nascimentos:
Distrito 1930 1949 1960
H M H M H M
Porto 13510 12881 16623 15453 18145 17082
Lisboa 10931 10392 10720 9500 12890 12095
Horta 581 546 643 606 475 432
Considerando os três distritos separadamente, e por anos, aprecie a qualidade dos
dados através da relação de masculinidade, calculando também quando necessário
intervalos de confiança.

95
10. No período de 1910 a 1990 numa certa região, veriﬁcaram-se movimentos naturais e
migratórios, dos quais só existem os seguintes registos:
1910 1920 1930 1940 1950 1960 1970 1980 1990
N 46 35 40 51 60 53 42 35 25
O 20 40 35 50 40 33 25 20 15
I 2 4 3 4 1 3 2 4 10
Ef 941 930 935 920 942 944 946 948 950
(a) Veriﬁque se existe alguma correlação entre os nascimentos e os óbitos naquela
região e ao longo do período registado. Se existe, de que tipo é?
(b) Usando a equação da concordância estime o número de emigrantes desse período
de 80 anos.
11. Aprecie a qualidade dos dados relativamente à atracção por valores terminados em 0
e 5 no registo das idades dos efectivos da freguesias de Botafogo, calculando o índice
de Whipple.
Id Id Id Id Id Id
0 e 1 30 14 16 27 15 40 15 53 5 66 4
2 26 15 12 28 19 41 7 54 8 67 3
3 25 16 12 29 13 42 8 55 9 68 4
4 23 17 14 30 20 43 7 56 4 69 3
5 15 18 16 31 9 44 6 57 3 70 5
6 20 19 18 32 8 45 16 58 7 71 2
7 13 20 23 33 13 46 8 59 8 72 2
8 15 21 19 34 11 47 6 60 12 73 4
9 16 22 15 35 17 48 5 61 5 74 1
10 22 23 13 36 11 49 6 62 4 75 e + 10
11 23 24 12 37 10 50 10 63 9
12 17 25 25 38 14 51 5 64 4
13 18 26 13 39 14 52 4 65 7

96
12. A repartição da população de um distrito por idade e por sexo é a seguinte:
Id H M Id H M Id H M Id H M
0 e 1 60 41 21 7 14 41 4 6 61 1 1
2 33 19 22 23 16 42 13 11 62 3 4
3 20 19 23 10 11 43 6 6 63 2 -
4 14 14 24 23 27 44 8 10 64 1 1
5 28 14 25 14 15 45 12 10 65 6 1
6 24 23 26 25 15 46 26 9 66 2 6
7 23 27 27 11 5 47 - 6 67 2 2
8 28 26 28 19 16 48 20 13 68 2 2
9 23 18 29 2 5 49 5 4 69 1 -
10 25 24 30 45 53 50 46 43 70 e + 17 22
11 18 18 31 6 7 51 - -
12 32 33 32 12 15 52 4 3
13 20 16 33 12 12 53 1 3
14 27 21 34 10 17 54 2 8
15 22 18 35 13 13 55 4 9
16 23 33 36 26 16 56 6 4
17 16 14 37 4 4 57 2 4
18 26 27 38 12 12 58 5 4
19 13 18 39 7 3 59 2 1
20 30 50 40 66 59 60 42 41 Total: 1097 1042
(a) Construa a pirâmide de idades usando grupos quinquenais.
(b) Aprecie a qualidade dos dados relativamente à atracção por valores terminados
em 0 e 5 nestes registos, calculando os índices de Whipple por sexo.
(c) Estude a atracção por valores terminados em 0 usando o índice de irregularidade.
13. Num determinado recenseamento a população masculina de 23 a 62 anos é de 1774524
e a feminina é de 2024972.
A população registada com 25, 30, 35, 40, 45, 50, 55 e 60 anos é de 364498 para a
população masculina e de 412637 para a população feminina.
Calcule os índices de Whipple para os dois sexos e conclua sobre a qualidade dos
dados.

97
14. Considere os seguintes dados por grupos de idades:
GI EM EF r.m. |Dif.Suc.| r.r. |r.r.-100| r.r. |r.r.-100|
×100
Ma Ma F F
0-4 388898 380729 – – – – –
5-9 387764 374444
10-14 329901 316366
15-19 338290 344489
20-24 303461 322174
25-29 247252 287879
30-34 202688 239092
35-39 189979 220078
40-44 172401 204964
45-49 150846 181026
50-54 143997 173833
55-59 117213 141652
60-64 101940 128179
65-69 71878 94306 – – – – –
70 e + 109368 160796 – – – – – –
Total 3255876 3570007
/12
Calcule o índice combinado das Nações Unidas. Que conclusões tira sobre a qualidade
dos dados?
15. No período 1951-1960, no nosso país, houve 2075500 nascimentos, 948705 óbitos,
353534 emigrantes oﬁciais e 15448 imigrantes. De França veio a seguinte informação:
9870 emigrantes clandestinos.
A população em 1950 era de 8441312 e em 1960 de 8889392.
Também se registou um saldo migratório com as colónias de I − E = −112482.
Conclua sobre a qualidade dos dados através da equação da concordância.
16. Construa a tábua de mortalidade a partir da repartição da população indicada na
ﬁgura 16.1, por grupos de idades.

98
PopulaçãoÓbitosTaxadeQuocientedeProbabilidadeSobreviventesDistribuiçãoNúmerodeProbabilidadeTotaldeanosEsperançade
mortalidademortalidadedenaidadexdosóbitosanosvividosdedepoisdaidadexvida
nmxnqxsobrevivênciasx+nndxnNxsobrevivênciaTxex
npxnPx
017485519277
1-47148599426
5-97986781528
10-14799693928
15-198109641551
20-247617032279
25-296812862256
30-345410991905
35-395673332301
40-445247372721
45-494600413148
50-543905663628
55-593317774412
60-642944395985
65-692299767408
70e+35653934162
Figura 16.1: Tábua de mortalidade

99
17. São conhecidos os seguintes dados, relativos a 1960, numa região da Europa:
Id N V P F O Taxa
mãe média F M
5mx
Total Legítimos Total Casada
15-19 736 564 29440 1178 490
20-24 4788 4750 23940 11970 414
25-29 5467 5356 27335 22779 498
30-34 3218 3101 22526 19252 435
35-39 1307 1290 23526 20007 485
40-44 546 540 27300 21050 607
45-49 123 119 24600 18223 601
Total 16185 15720 178667 114459
A população média é de 720025.
(a) Calcule a taxa bruta de natalidade;
(b) Calcule a taxa de fecundidade geral;
(c) Calcule a taxa de fecundidade legítima;
(d) Calcule a taxa de fecundidade ilegítima;
(e) Veriﬁque se foram correctamente calculadas as taxas das duas primeiras alíneas;
(f) Calcule as taxas de fecundidade geral e as taxas de fecundidade legítima por
grupos de idades;
(g) Calcule a descendência média e as taxas bruta e líquida de reprodução. Inter-
prete os resultados obtidos;
Id t.f.g. t.f.l. Quociente Prob. t.f.g.×
mãe M (5qx) sobrevivência 5px
5px
15-19
20-24
25-29
30-34
35-39
40-44
45-49
Total
(h) Calcule a idade média da fecundidade, Mx, a variância, σ2
, e as proporções
de mulheres casadas. Ajuste estas proporções a 100 bem como as taxas de
fecundidade geral. Represente graﬁcamente e comente os resultados.

100
Id t.f.g. PMIG t.f.g.×Ix Ix − MI Ix − MI
2
t.f.g.
mãe ×
x − ... Ix Ix − MI
2
15-19 17.5
20-24 22.5
25-29 27.5
30-34 32.5
35-39 37.5
40-44 42.5
45-49 47.5
Total - - -
Id P F Prop F Ajuste a Ajuste
mãe média casadas 100 das a 100 das
Total Casada Prop. t.f.g.
15-19 29440 1178
20-24 23940 11970
25-29 27335 22779
30-34 22526 19252
35-39 23526 20007
40-44 27300 21050
45-49 24600 18223
100
50
15-19 20-24 25-29 30-34 35-39 40-44 45-49 GI
18. Dispomos dos seguintes dados, relativos ao período de 1929-1932, numa região de

101
Portugal:
GI C solteiros R solteiros Taxas NU Taxas NU
1929-1932 de 1930 Ma F
Ma F Ma F 5nx 5nx
15-19 149 797 32880 32530
20-24 1967 2050 25308 22667
25-29 1391 878 10872 11305
30-34 384 249 4848 6451
35-39 128 97 3136 4576
40-44 69 47 2135 3599
45-49 31 21 1667 3091
50 e + 37 17 5343 10871
Total
A população masculina total é de 326579.
A população feminina total é de 357001.
(a) Calcule a taxa bruta de nupcialidade;
(b) Calcule a taxa de nupcialidade geral (dos solteiros);
(c) Calcule as taxas de nupcialidade por grupos de idades e por sexos;
(d) Calcule as tábuas de nupcialidade para ambos os sexos;
GI Prob Prob Sobreviventes DI de C
Ma do 1o
C sobreviver na idade x entre idades
ao 1o
C
5qx 5px Cx 5dx
15-19 100000
20-24
25-29
30-34
35-39
40-44
45-59
50 e +

102
GI Prob Prob Sobreviventes DI de C
F do 1o
C sobrevivier na idade x entre idades
ao 1o
C
5qx 5px Cx 5dx
15-19 100000
20-24
25-29
30-34
35-39
40-44
45-59
50 e +

103
(e) Calcule o celibato definitivo (CD), a intensidade do casamento (I) e a idade
média no primeiro casamento (X) para ambos os sexos.
Grupo DI de C PMIG 5dx × Ix DI de C PMIG 5dx × Ix
de entre idades entre idades
idades 5dx 5dx
x − ... Ma Ix Ma F Ix F
15-19 17.5 17.5
20-24 22.5 22.5
25-29 27.5 27.5
30-34 32.5 32.5
35-39 27.5 37.5
40-44 42.5 32.5
45-49 47.5 47.5
Total - -
19. São conhecidos os seguintes dados numa determinada região de Portugal:
População em 1960 276895
População em 1970 205197
Nascimentos entre 1961-1970 (10 anos) 41053
Óbitos entre 1961-1970 (10 anos) 25760
Emigrantes entre 1961-1970 (10 anos) 9009
Imigrnates entre 1961-1970 (10 anos) 18
Emigrantes oficiais a nível do país entre 1961-1970 681004
Emigrantes clandestinos a nível do país entre 1961-1970 517385
Os emigrantes clandestinos a nível do país foram calculados pela equação da concor-
dância, uma vez que no país não existem migrações internas.
(a) Calcule a taxa bruta de emigração;
(b) Calcule a taxa bruta de imigração;
(c) Calcule a taxa bruta de migração total;
(d) Através da equação da concordância calcule o saldo (movimento) migratório
total. Compare com os dados oficiais. Interprete os reultados;
(e) Estime o número real de emigrantes (=oficiais+clandestinos);
(f) Calcule o saldo migratório externo;
(g) Calcule o saldo migratório interno;
(h) Calcule a taxa bruta de emigração real;
(i) Calcule a taxa bruta de migração externa líquida;
(j) Calcule a taxa bruta de migração interna líquida.

Tabela de números aleatórios
Linha
101 19223 95034 05756 28713 96409 12531 42544 82853
102 73676 47150 99400 01927 27754 42648 82425 36290
103 45467 71709 77558 00095 32863 29485 82226 90056
104 52711 38889 93074 60227 40011 85848 48767 52573
105 95592 94007 69971 91481 60779 53791 17297 59335
106 68417 35013 15529 72765 85089 57067 50211 47487
107 82739 57890 20807 47511 81676 55300 94383 14893
108 60940 72024 17868 24943 61790 90656 87964 18883
109 36009 19365 15412 39638 85453 46816 83485 41979
110 38448 48789 18338 24697 39364 42006 76688 08708
111 81486 69487 60513 09297 00412 71238 27649 39950
112 59636 88804 04634 71197 19352 73089 84898 45785
113 62568 70206 40325 03699 71080 22553 11486 11776
114 45149 32992 75730 66280 03819 56202 02938 70915
115 61041 77684 94322 24709 73698 14526 31893 32592
116 14459 26056 31424 80371 65103 62253 50490 61181
117 38167 98532 62183 70632 23417 26185 41448 75532
118 73190 32533 04470 29669 84407 90785 65956 86382
119 95857 07118 87664 92099 58806 66979 98624 84826
120 35476 55972 39421 65850 04266 35435 43742 11937
105

TABELA DE NÚMEROS ALEATÓRIOS 106
Linha
121 71487 09984 29077 14863 61683 47052 62224 51025
122 13873 81598 95052 90908 73592 75186 87136 95761
123 54580 81507 27102 56027 55892 33063 41842 81868
124 71035 09001 43367 49497 72719 96758 27611 91596
125 96746 12149 37823 71868 18442 35119 62103 39244
126 96927 19931 36089 74192 77567 88741 48409 41903
127 43909 99477 25330 64359 40085 16925 85117 36071
128 15689 14227 06565 14374 13352 49367 81982 87209
129 36759 58984 68288 22913 18638 54303 00795 08727
130 69051 64817 87174 09517 84534 06489 87201 97245
131 05007 16632 81194 14873 04197 85576 45195 96565
132 68732 55259 84292 08796 43165 93739 31685 97150
133 45740 41807 65561 33302 07051 93623 18132 09547
134 27816 78416 18329 21337 35213 37741 04312 68508
135 66925 55658 39100 78458 11206 19876 87151 31260
136 08421 44753 77377 28744 75592 08563 79140 92454
137 53645 66812 61421 47836 12609 15373 98481 14592
138 66831 68908 40772 21558 47781 33586 79177 06928
139 55588 99404 70708 41098 43563 56934 48394 51719
140 12975 13258 13048 45144 72321 81940 00360 02428
141 96767 35964 23822 96012 94591 65194 50842 53372
142 72829 50232 97892 63408 77919 44575 14870 04178
143 88565 42628 17797 49376 61762 16953 88604 12724
144 62964 88145 83083 69453 46109 59505 69680 00900
145 19687 12633 57857 95806 09931 02150 43163 58636
146 37609 59057 66967 83401 60705 02384 90597 93600
147 54873 86278 88737 74351 47500 84552 19909 67181
148 00694 05977 19664 65441 20903 62371 22725 53340
149 71546 05233 53946 68743 72460 27601 45403 88692
150 07511 88915 41267 16853 84569 79367 32337 03316
151 0380. 29341 29264 80198 12371 13121 54969 43912
152 77320 35030 77519 41109 98296 18984 60869 12349
153 07886 56866 39648 69290 03600 05376 58958 22720
154 87065 74133 21117 70595 22791 67306 28420 52067
155 42090 09628 54035 93879 98441 04606 27381 82637
156 55494 67690 88131 81800 11188 28552 25752 21953
157 16698 30406 96587 65985 07165 50148 16201 86792
158 16297 07626 68683 45335 34377 72941 41764 77038
159 22897 17467 17638 70043 36243 13008 83993 22869
160 98163 45944 34210 64158 76971 27689 82926 75957

TABELA DE NÚMEROS ALEATÓRIOS 107
Linha
161 43400 25831 06283 22138 16043 15706 73345 26238
162 97341 46254 88153 62336 21112 35574 99271 45297
163 64578 67197 28310 90341 37531 63890 52630 76315
164 11022 79124 49525 63078 17229 32165 01343 21394
165 81232 43939 23840 05995 84589 06788 76358 26622
166 36843 84798 51167 44728 20554 55538 27647 32708
167 84329 80081 69516 78934 14293 92478 16479 26974
168 27788 85789 41592 74472 96773 27090 24954 41474
169 99224 00850 43737 75202 44753 63236 14260 73686
170 38075 73239 52555 46342 13365 02182 30443 53229
171 87368 49451 53771 48343 51236 18522 73670 23212
172 40512 00681 44282 47178 08139 78693 34715 75606
173 81636 57578 54286 27216 58758 80358 84115 84568
174 26411 94292 06340 97762 37033 85968 94165 46514
175 80011 09937 57195 33906 94831 10056 42211 65491
176 92813 87503 63494 71379 76550 45984 05481 50830
177 70348 72871 63419 57363 29685 43090 18763 31714
178 24005 52114 26224 39078 80798 15220 43186 00976
179 85063 55810 10470 08029 30025 29734 61181 72090
180 11532 73186 92541 06915 72954 10167 12142 26492
181 59618 03914 05208 84088 20426 39004 84582 87317
182 92965 50837 39921 84661 82514 81899 24565 60874
183 85116 27684 14597 85747 01596 25889 41998 15635
184 15106 10411 90221 49377 44569 28185 80959 76355
185 03638 31589 07871 25792 85823 55400 56026 12193
186 97971 48932 45792 63993 95635 28753 46069 84635
187 49345 18305 76213 82390 77412 97401 50650 71755
188 87370 88099 89695 87633 76987 85503 26257 51736
189 88296 95670 74932 65317 93848 43988 47597 83044
190 79485 92200 99401 54473 34336 82796 05457 60343
191 40830 24979 23333 37619 56227 95941 59494 86539
192 32006 76302 81221 00693 95197 75044 46596 11628
193 37569 85187 44692 50706 53161 69027 88389 60313
194 56680 79003 23361 67094 15019 63261 24543 52884
195 05172 08100 22316 54495 60005 29532 18433 18057
196 74782 27005 03894 98038 20627 40307 47317 92759
197 85228 93264 61409 03404 09649 55937 60843 66167
198 68309 12060 14762 58002 03716 81968 57934 32624
199 26461 88346 52430 60906 74216 96263 69296 90107
200 42672 67680 42376 95023 82744 03971 96560 55148

Bibliografia
[1] M. N. Amorim. Evolução Demográfica de 3 Paróquias no Sul do Pico 1680-1980, vo-
lume 35. ICS, U.M., 1992.
[2] B. J. F. Murteira e G. H. J. Black. Estatística Descritiva. Editora McGraw-Hill, 1983.
[3] J. M. Nazareth. Princípios e Métodos de Análise da Demografia Portuguesa. Editorial
Presença, 1988.
108

Estatística

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Estatística

Mais de Universidade Federal Fluminense

Último

Estatística