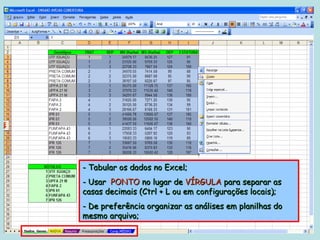
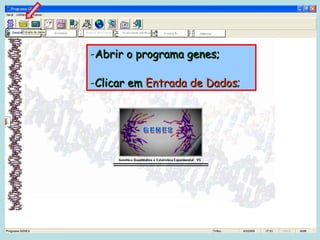
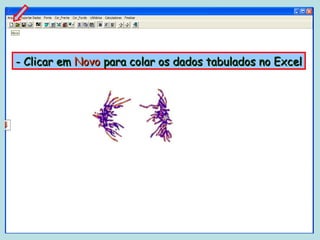
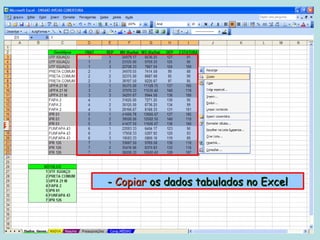
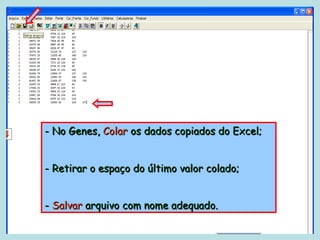
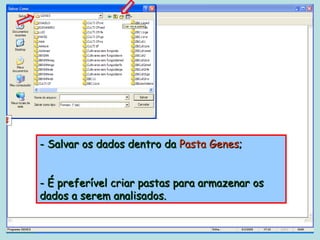
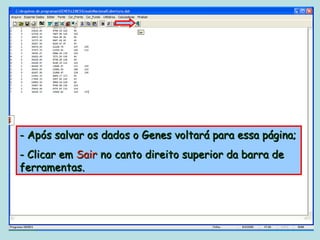
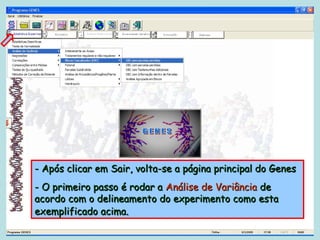
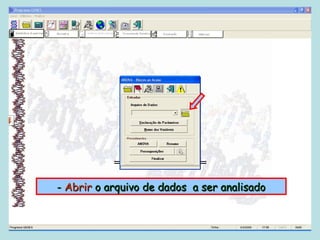
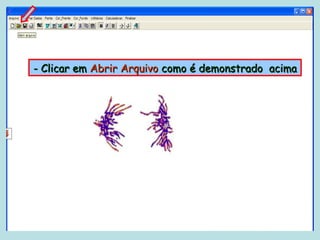
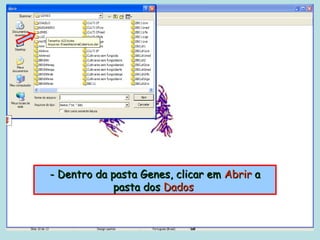
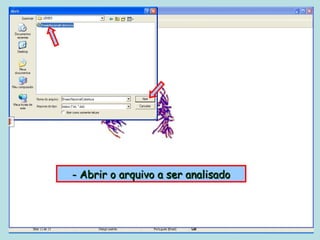
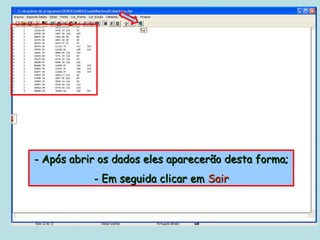
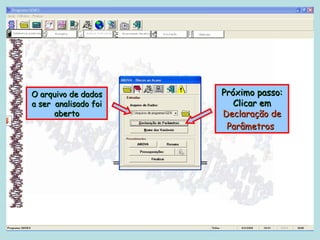
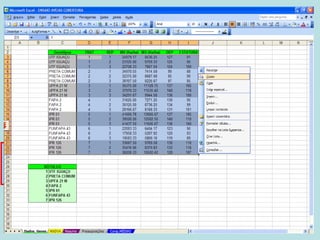
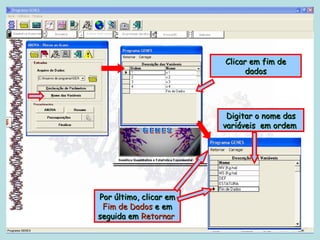
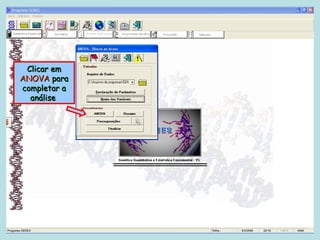
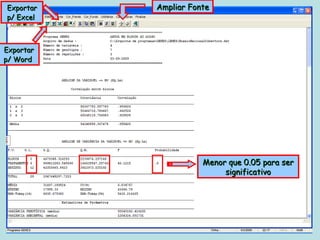
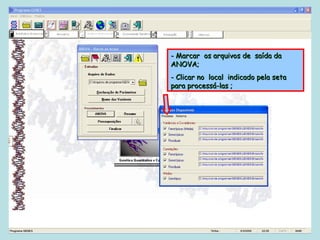
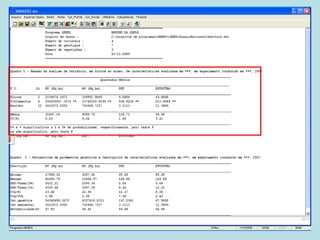
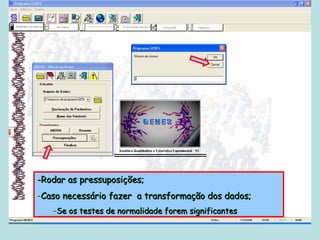
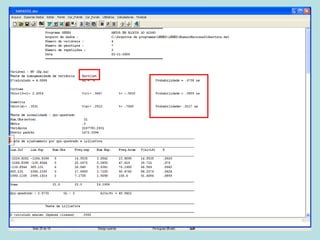
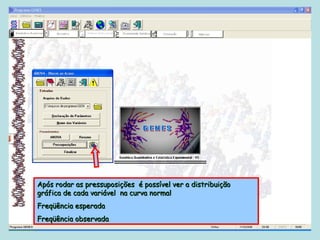
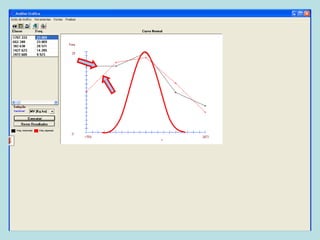
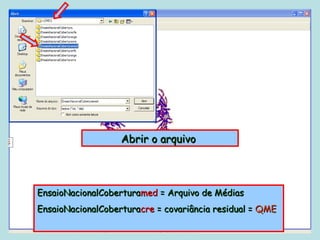
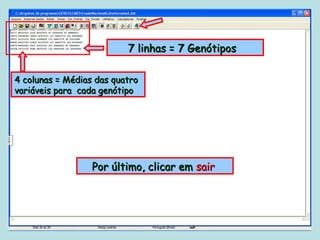
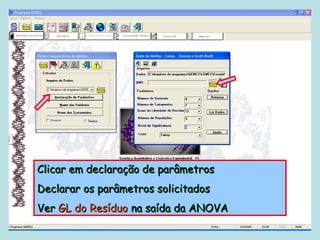
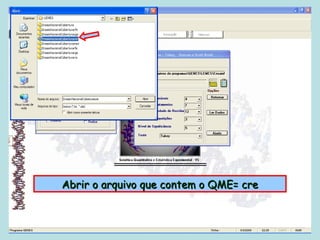
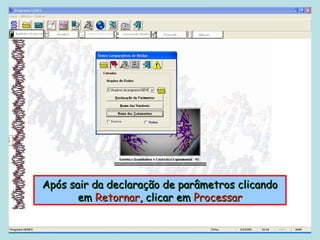
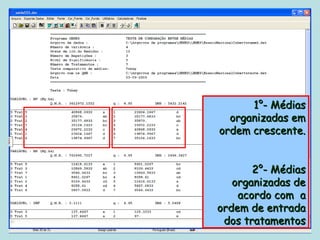
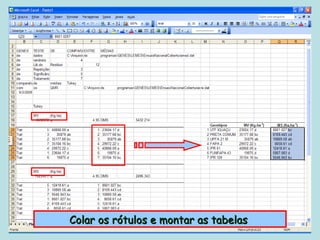
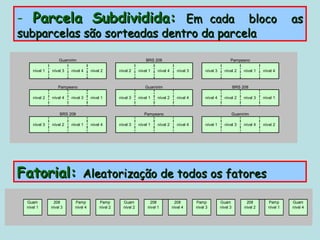
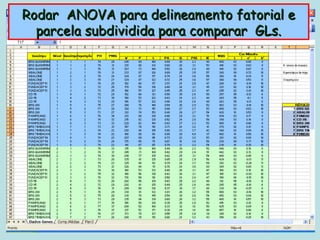
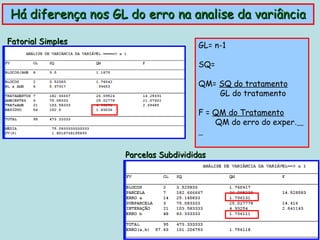
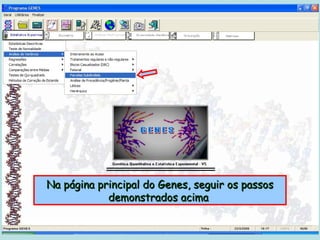
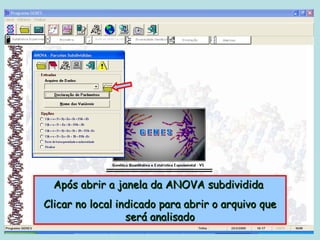
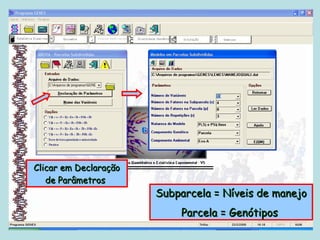
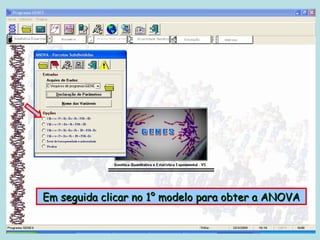
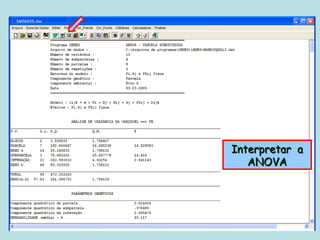
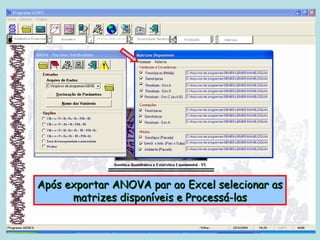
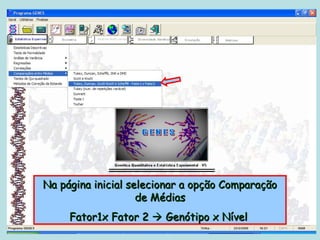
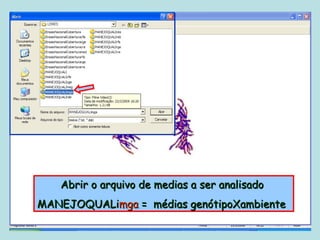
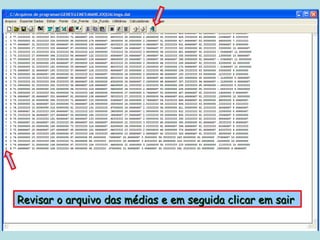
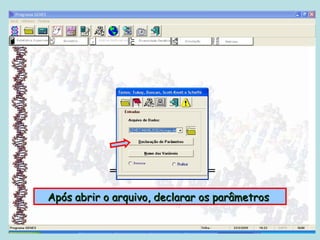
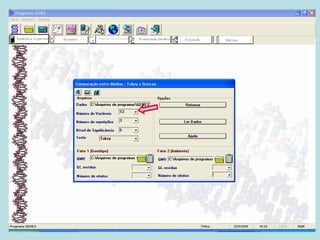
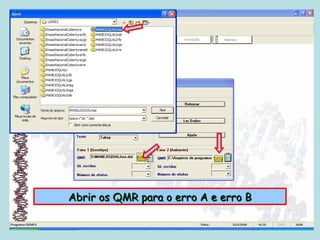
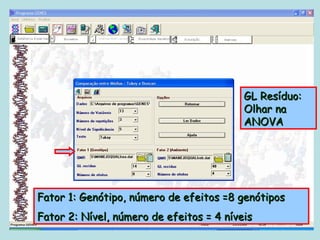
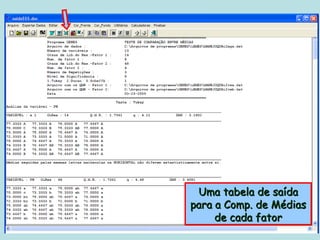
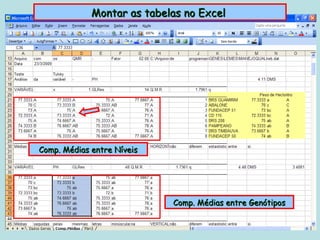
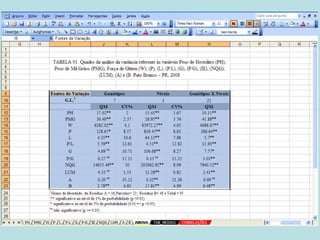
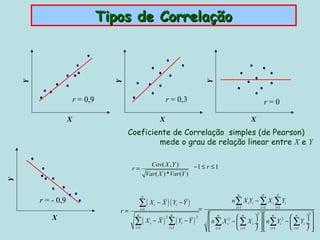
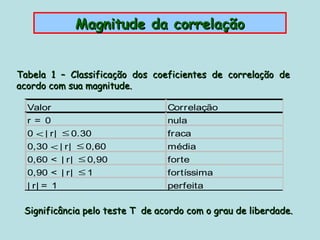
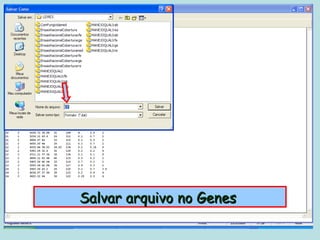
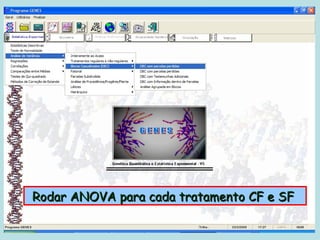
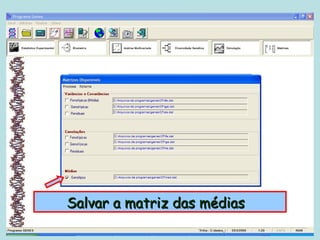
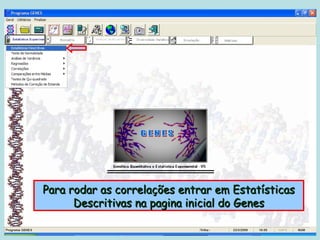
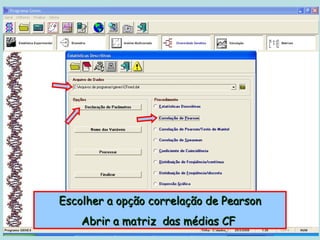
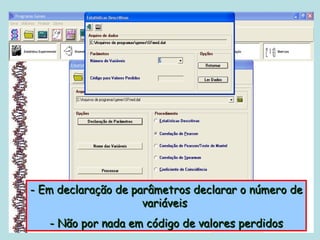
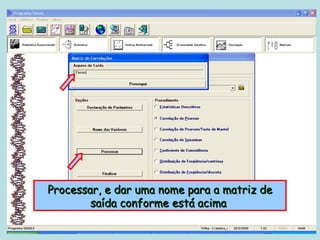
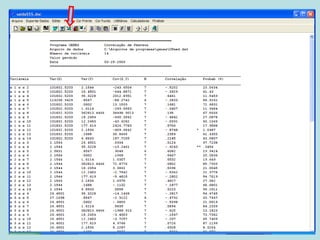
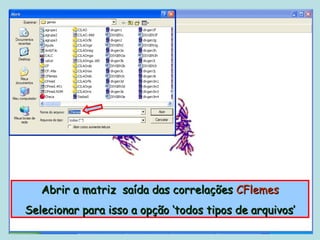
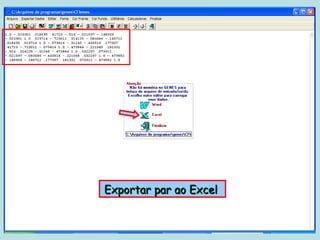
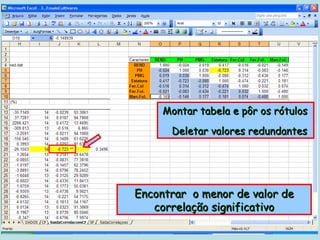
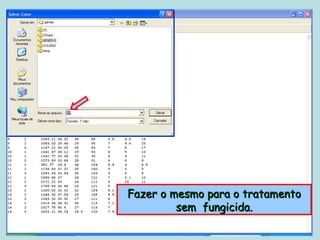
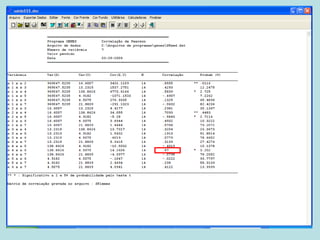
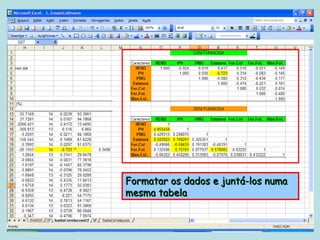
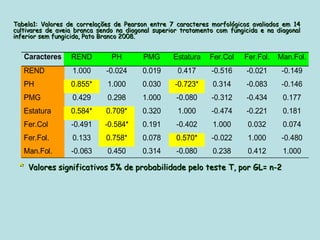
Este documento fornece instruções sobre como realizar análises estatísticas usando o programa Genes. Ele explica como carregar e salvar dados, declarar parâmetros, rodar análises de variância, comparações de médias, correlações e exportar resultados para o Excel.

1. Genes
Cristiano Lemes

2. Análises
• Análise de Variância
• Comparação de Médias
• Parcelas Subdivididas
• Experimentos Fatoriais
• Correlações

3. Análise de Variância
O objetivo da análise de variância é avaliar se as diferenças
observadas entre as médias das amostras são estatisticamente
significantes.
Teste F
Aceitar ou rejeitar H0

4. - Tabular os dados no Excel;
- Usar PONTO no lugar de VÍRGULA para separar as
casas decimais (Ctrl + L ou em configurações locais);
- De preferência organizar as análises em planilhas do
mesmo arquivo;

5. -Abrir o programa genes;
-Clicar em Entrada de Dados;

6. - Clicar em Novo para colar os dados tabulados no Excel

7. - Copiar os dados tabulados no Excel

8. - No Genes, Colar os dados copiados do Excel;
- Retirar o espaço do último valor colado;
- Salvar arquivo com nome adequado.

9. - Salvar os dados dentro da Pasta Genes;
- É preferível criar pastas para armazenar os
dados a serem analisados.

10. - Após salvar os dados o Genes voltará para essa página;
- Clicar em Sair no canto direito superior da barra de
ferramentas.

11. - Após clicar em Sair, volta-se a página principal do Genes
- O primeiro passo é rodar a Análise de Variância de
acordo com o delineamento do experimento como esta
exemplificado acima.

12. - Abrir o arquivo de dados a ser analisado

13. - Clicar em Abrir Arquivo como é demonstrado acima

14. - Dentro da pasta Genes, clicar em Abrir a
pasta dos Dados

15. - Abrir o arquivo a ser analisado

16. - Após abrir os dados eles aparecerão desta forma;
- Em seguida clicar em Sair

17. O arquivo de dados Próximo passo:
a ser analisado foi Clicar em
aberto Declaração de
Parâmetros

18. Ver o arquivo do Excel para declarar quantas
variáveis estarão sendo analisadas
Por fim, clicar em
Número de genótipos ou Retornar
tratamentos
correspondem a 1a coluna
do arquivo de dados Número de blocos ou
repetições
correspondem a 2a

19. Clicar em fim de
dados
Digitar o nome das
variáveis em ordem
Por último, clicar em
Fim de Dados e em
seguida em Retornar

20. Clicar em
ANOVA para
completar a
análise

21. Exportar Ampliar Fonte
p/ Excel
Exportar
p/ Word
Menor que 0.05 para ser
significativo

22. - Marcar os arquivos de saída da
ANOVA;
- Clicar no local indicado pela seta
para processá-las ;

24. -Rodar as pressuposições;
-Caso necessário fazer a transformação dos dados;
-Se os testes de normalidade forem significantes

26. Após rodar as pressuposições é possível ver a distribuição
gráfica de cada variável na curva normal
Freqüência esperada
Freqüência observada

29. Comparação de Médias
- Serve como um complemento para o estudo da análise de variância
-Fazendo apenas o teste de “f” (teste que mostra se existe diferença
entre as médias dos tratamentos) não podemos indicar qual o melhor
tratamento.
-Neste caso, é necessário aplicar um teste de comparação de médias
dos tratamentos, daí então podendo concluir qual o melhor
tratamento.

30. - Página principal do Genes
Estatística experimentaisComparações entre Médias  Tukey, Ducan,
SNK, Dunnet, Teste T entre outros.

31. Procurar o arquivo de Médias a ser analisado

32. Clicar no local indicado pela seta acima para
encontrar o arquivo das médias

33. Abrir o arquivo
EnsaioNacionalCoberturamed = Arquivo de Médias
EnsaioNacionalCoberturacre = covariância residual = QME

34. 7 linhas = 7 Genótipos
4 colunas = Médias das quatro
variáveis para cada genótipo
Por último, clicar em sair

35. Clicar em declaração de parâmetros
Declarar os parâmetros solicitados
Ver GL do Resíduo na saída da ANOVA

36. Abrir o arquivo que contem o QME= cre

37. Após sair da declaração de parâmetros clicando
em Retornar, clicar em Processar

38. 1°- Médias
organizadas em
ordem crescente.
2°- Médias
organizadas de
acordo com a
ordem de entrada
dos tratamentos

39. Colar os rótulos e montar as tabelas

40. Parcelas Subdivididas
X
Fatorial
Quando usar um ou o outro delineamenento?
Quais são as diferenças ?

41. - Parcela Subdividida: Em cada bloco as
subparcelas são sorteadas dentro da parcela
Guamirim BRS 208 Pampeano
nível 1 nível 3 nível 4 nível 2 nível 2 nível 1 nível 4 nível 3 nível 3 nível 2 nível 1 nível 4
Pampeano Guamirim BRS 208
nível 2 nível 4 nível 3 nível 1 nível 3 nível 1 nível 2 nível 4 nível 4 nível 2 nível 3 nível 1
BRS 208 Pampeano Guamirim
nível 3 nível 2 nível 1 nível 4 nível 3 nível 1 nível 2 nível 4 nível 1 nível 3 nível 4 nível 2
Fatorial: Aleatorização de todos os fatores
Guam 208 Pamp Pamp Guam 208 208 Pamp Guam 208 Pamp Guam
nível 1 nível 3 nível 4 nível 2 nível 2 nível 1 nível 4 nível 3 nível 3 nível 2 nível 1 nível 4

42. Rodar ANOVA para delineamento fatorial e
parcela subdividida para comparar GLs.

43. Há diferença nos GL do erro na analise da variância
Fatorial Simples GL= n-1
SQ=
QM= SQ do tratamento
GL do tratamento
F = QM do Tratamento
QM do erro do exper.
Parcelas Subdivididas

44. Copiar os dados do Excel para o Genes

45. Não esquecer de retirar o último espaço

46. Salvar o arquivo

47. Na página principal do Genes, seguir os passos
demonstrados acima

48. Após abrir a janela da ANOVA subdividida
Clicar no local indicado para abrir o arquivo que
será analisado

49. Clicar em Declaração
de Parâmetros
Subparcela = Níveis de manejo
Parcela = Genótipos

50. Em seguida clicar no 1° modelo para obter a ANOVA

51. Interpretar a
ANOVA

52. Após exportar ANOVA par ao Excel selecionar as
matrizes disponíveis e Processá-las

53. Na página inicial selecionar a opção Comparação
de Médias
Fator1x Fator 2  Genótipo x Nível

54. Abrir o arquivo de medias a ser analisado
MANEJOQUALimga = médias genótipoXambiente

55. Revisar o arquivo das médias e em seguida clicar em sair

56. Após abrir o arquivo, declarar os parâmetros

58. Abrir os QMR para o erro A e erro B

59. GL Resíduo:
Olhar na
ANOVA
Fator 1: Genótipo, número de efeitos =8 genótipos
Fator 2: Nível, número de efeitos = 4 níveis

60. Uma tabela de saída
para a Comp. de Médias
de cada fator

61. Montar as tabelas no Excel
Comp. Médias entre Níveis
Comp. Médias entre Genótipos

64. Correlação
- Existe correlação entre duas variáveis quando a
alteração sofrida por uma delas é acompanhada por
modificações na outra.
- Seleção indireta no melhoramento de plantas
- caracteres de dificuldade medição ou identificação
Definir estratégias de seleção para as gerações seguintes;
Verificar se os caracteres tendem a permanecer associados
durante os sucessivos ciclos de seleção.

65. Tipos de Correlação
Y
Y
Y
r = 0,9 r = 0,3 r=0
X X X
Coeficiente de Correlação simples (de Pearson)
mede o grau de relação linear entre X e Y
Cov ( X , Y ) −1 ≤ r ≤ 1
r=
Var ( X ) *Var (Y )
Y
n n n
n ∑ X iYi − ∑ X i ∑ Yi
n
r = - 0,9 ∑( X i − X ) ( Yi − Y )
r= i =1 = i =1 i =1 i =1
X
n n  n 2  n   n 2  n  
2 2
∑( X −X) ∑( Y − Y )  n ∑ X i −  ∑ X i ÷   n ∑Yi −  ∑Yi ÷ 
2 2
i i
i =1 i =1  i =1
  i =1    i =1
  i =1  

66. Magnitude da correlação
Tabela 1 – Classificação dos coeficientes de correlação de
acordo com sua magnitude.
Valor Correlação
r = 0 nula
0 < | r| ≤ 0.30 fraca
0,30 < | r| ≤ 0,60 média
0,60 < | r| ≤ 0,90 forte
0,90 < | r| ≤ 1 fortíssima
| r| = 1 perfeita
Significância pelo teste T de acordo com o grau de liberdade.

68. Salvar arquivo no Genes

69. Rodar ANOVA para cada tratamento CF e SF

70. Salvar a matriz das médias

71. Para rodar as correlações entrar em Estatísticas
Descritivas na pagina inicial do Genes

72. Escolher a opção correlação de Pearson
Abrir a matriz das médias CF

73. - Em declaração de parâmetros declarar o número de
variáveis
- Não por nada em código de valores perdidos

74. Processar, e dar uma nome para a matriz de
saída conforme está acima

76. Abrir a matriz saída das correlações CFlemes
Selecionar para isso a opção ‘todos tipos de arquivos’

77. Exportar par ao Excel

78. Montar tabela e pôr os rótulos
Deletar valores redundantes
Encontrar o menor de valor de
correlação significativo

79. Fazer o mesmo para o tratamento
sem fungicida.

81. Abrir a matriz saída das correlações SFlemes
Exportar isso para o Excel e fazer as formatações
necessárias.

82. Formatar os dados e juntá-los numa
mesma tabela

83. Tabela1: Valores de correlações de Pearson entre 7 caracteres morfológicos avaliados em 14
cultivares de aveia branca sendo na diagonal superior tratamento com fungicida e na diagonal
inferior sem fungicida, Pato Branco 2008.
Caracteres REND PH PMG Estatura Fer.Col Fer.Fol. Man.Fol.
REND 1.000 -0.024 0.019 0.417 -0.516 -0.021 -0.149
PH 0.855* 1.000 0.030 -0.723* 0.314 -0.083 -0.146
PMG 0.429 0.298 1.000 -0.080 -0.312 -0.434 0.177
Estatura 0.584* 0.709* 0.320 1.000 -0.474 -0.221 0.181
Fer.Col -0.491 -0.584* 0.191 -0.402 1.000 0.032 0.074
Fer.Fol. 0.133 0.758* 0.078 0.570* -0.022 1.000 -0.480
Man.Fol. -0.063 0.450 0.314 -0.080 0.238 0.412 1.000
* Valores significativos 5% de probabilidade pelo teste T, por GL= n-2

84. OBRIGADO!
cristianolemes.utfpr@gmail.com