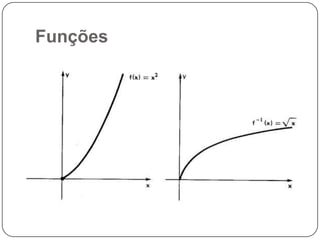
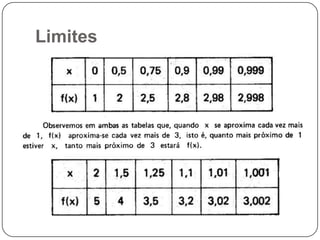
O documento discute derivadas e integrais. Introduz derivadas como uma forma de analisar variações em dados numéricos e define derivadas matematicamente. Também apresenta regras básicas para derivadas de soma, subtração, multiplicação e divisão. Integrais são definidas como a operação inversa da derivada para recuperar a função original a partir de sua derivada. Regras básicas para integrais de soma, constante e variável com expoente são fornecidas.

1. Derivadas e Integrais
Isis Vasconcelos de Brito
isis@if.usp.br
FATEC/SP – Física Aplicada I

2. Funções

3. Funções

4. Limites

5. Limites

6. Derivadas

Derivação = um processo destinado a
analisar as variações no comportamento
de um conjunto de dados numéricos.
Forma de analisar vários problemas sob a
ótica infinitesimal (das pequenas
variações).

7. Derivadas
 Definimos como coeficiente angular de
uma reta:
 Considerando a função f(x), teríamos
sobre o seu gráfico os pontos:

8. Derivadas
 Podemos, a partir desta equação,
encontrar os valores de m e verificar
qual a inclinação aproximada da
curva para cada ponto;
 Quando
diminuímos o módulo
de Δx a equação se torna mais
precisa, no sentido de fornecer uma
melhor
aproximação
para
o coeficiente angular de um
pequeno trecho da curva.

9. Derivadas
 Uma maneira de tornar a inclinação da
reta mais próxima da inclinação da
função é diminuir a distância entre os
pontos até o limite de sua aproximação:

10. Derivadas
 O artifício de criar uma função que nos dá a
declividade de uma outra função em cada
ponto é chamado de derivação, uma vez
que criamos uma função que é
a derivada da primeira.

11. Derivadas - Regras
 Soma e Subtração:
 Multiplicação:

12. Derivadas - Regras
 Divisão:

13. Derivadas básicas
 Constante:
 Fator Constante:

14. Derivadas básicas
 Variável com expoente constante:

15. Integrais
Se é possível criar uma função a partir
de outra utilizando a diferenciação, o que
teríamos se fizéssemos a operação
inversa?
 Artifício para recuperar a função original
a partir da sua derivada.
 O valor numérico de uma integral definida
exatamente
em
um
intervalo
é
correspondente ao valor da área do
desenho delimitado pela curva da função


16. Integrais
 Ao
operar
a
inversa
da
derivada, podemos fazer a análise com
as diferenciais, ou seja, considere a
função y = f(x) + C

17. Integrais
 Esta operação é chamada de
antidiferencial e é simbolizada por:
Onde (f) é a função e (d) é a
diferencial da variável independente

18. Integrais básicas
 Diferencial dx:
 Constante:

19. Integrais básicas
 Adição:
 Variável com expoente constante:

20. Integral Definida
Suponha que você conheça a taxa f(x)
= dF/dx, na qual uma certa grandeza F
está variando e deseje encontrar a
quantidade pela qual a grandeza F
variará entre x = a e x = b. Você pode
primeiro
encontrar
F
por
antidiferenciação, e então calcular a
diferença:

números a e b são denominados limites de integração

21. Integral Definida

22. Integral Definida
 Teorema fundamental do Cálculo: