Cálculo Numérico - Integração Numérica

Aula 16
Integração Numérica

Aula 16 – Integração Numérica
Cálculo Numérico 3/41
Integração
Numérica

¨  Em determinadas situações, integrais são difíceis, ou
mesmo impossíveis de se resolver analiticamente.
¨  Em alguns casos, o valor de f (x) é conhecido apenas em
alguns pontos, num intervalo [a, b]. Como não se conhece a
expressão analítica de f (x), não é possível calcular:
∫
b
a
dxxf )(

¨ 
¨  Substituição da função f (x) por um polinômio que a aproxime
razoavelmente no intervalo [a, b].

¨  As fórmulas terão a expressão:
f (x)dx
a
b
∫ ≈ A0 f (x0 )+ A1 f (x1)+...+ An f (xn ),
xi ∈ [a,b],i = 0,1,...,n
∑=
=
n
i
iin xfAfI
0
)()(

¨  Fórmulas de Newton-Cotes Fechadas
¤  Regra dos Trapézios, x0 = a e xn = b.
¤  Regra 1/3 de Simpson.
¨  Fórmulas de Newton-Cotes Abertas
¤  os xi têm de pertencer ao intervalo aberto de a até b.

Fórmulas de Newton-Cotes
¨  A ideia de polinômio que aproxime f (x) razoavelmente, é
que este polinômio interpole f (x) em pontos de [a, b]
igualmente espaçados.
¨  Considere a partição do intervalo [a, b] em subintervalos, de
comprimento h, [xi, xi+1], i = 0, 1, ..., n – 1. Assim:
xi+1 − xi = h =
b− a( )
n

¨  Desta forma, as fórmulas de Newton-Cotes são
fórmulas de integração do tipo:
sendo os coeficientes Ai determinados de acordo com o grau do
polinômio aproximador.
x0 = a, xn = b
f (x)dx
a
b
∫ = f (x)dx
x0
xn
∫ ≈ Ai f (xi )
i=0
n
∑

¨  Diferença entre as fórmulas de Newton-Cotes fechadas (a) e
abertas (b).

¨  Utilizando a interpolação polinomial na Forma de Lagrange:
1º Polinômio de LagrangeREGRA DOS
TRAPÉZIOS
2º Polinômio de LagrangeREGRA 1/3
DE SIMPSON

Regra dos Trapézios

¨  Usaremos a para expressar P1 (x) que
interpola f (x) em x0 e x1:
¨  Então:
P1 x( )= f x0( )
x − x1
x0 − x1
+ f x1( )
x − x0
x1 − x0
f x( )dx =
a
b
∫ P1 x( )
x0
x1
∫ dx = f x0( )
x − x1
x0 − x1
+ f x1( )
x − x0
x1 − x0
#
$
%
&
'
(
x0
x1
∫ dx

¨  Resolvendo a integração:
ou seja:
( ) ( ) ( )[ ]10
01
2
xfxf
xx
IT
+
−
=
( ) ( )[ ]10
2
xfxf
h
IT
+=

¤  Consiste em considerar um polinômio de primeiro grau que
aproxima uma função f (x), ou seja, n = 1.
¤  Este polinômio terá a forma y = α0 + α1x e trata-se da equação
que une dois pontos: a = x0 e b = x1.
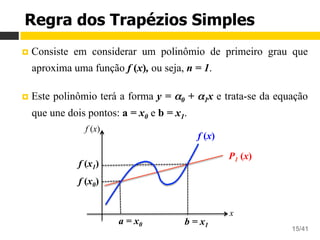
Regra dos Trapézios Simples
f (x1)
f (x0)
a = x0 b = x1
f (x)
P1 (x)
x
f (x)

f (x)dx ≈
h
2
f (x0 )+ f (x1)[ ]
x0
x1
∫
T = f (x1)
t = f (x0)
a = x0 b = x1
f (x)
P1 (x)
x
f (x)
h
f (x0)
f (x1)
Área do trapézio: A = h (T + t) / 2
De acordo com a figura:
¤  b – a = x1 – x0= h
¤  f (b) = f (x1) = T
¤  f (a) = f (x0) = t
¤  h - altura do trapézio
¤  t - base menor
¤  T - base maior
Logo,

¨ 
¤  Aproximação do valor da integral é aceitável.
¨ 
¤  Aproximação não indicada.

x1
¨  Intervalo [a, b] de grande amplitude.
¨  Soma da área de n trapézios, cada qual definido pelo seu
sub-intervalo.
Regra dos Trapézios Repetida (Composta)
x0 xn x
f (x)
x1 xn-1. . .

¨ 
¤  Aproximação do valor da integral é aceitável.
¨ 
¤  Aproximação não indicada.
¤  Uso da Regra dos Trapézios Repetida (Composta): soma da área
de n trapézios, cada qual definido pelo seu sub-intervalo.
¤  A amplitude dos sub-intervalos será h = (b - a) / n.
¤  A integral no intervalo é dada pela soma das integrais definidas
pelos sub-intervalos.

¨  Fórmula:
¨  Só os termos f (x0) e f (xn) não se repetem, assim, esta
fórmula pode ser simplificada em:
f (x)dx ≈
h
2
f (x0 )+ f (x1)[ ]+
x0
xn
∫
h
2
f (x1)+ f (x2 )[ ]
+...+
h
2
f (xn−1)+ f (xn )[ ]
f (x)dx ≈
h
2
f (x0 )+ 2 f (x1)+ f (x2 )+...+ f (xn−1)[ ]+ f (xn ){ }
x0
xn
∫
Regra dos Trapézios Repetida

¨  Regra dos Trapézios Simples - 1 subintervalo
I ≈ 2,48508
¨  Regra dos Trapézios Repetida - 2 subintervalos
I ≈ 2,1369
¨  Regra dos Trapézios Repetida – 8 subintervalos
I ≈ 2,0936
x y = (1 + x²)-1/2
0,0 1,00000
0,5 0,89445
1,0 0,70711
1,5 0,55475
2,0 0,44722
2,5 0,37138
3,0 0,31623
3,5 0,27473
4,0 0,24254
A aproximação para 8 subintervalos é
melhor, dado que o .
Estimar o valor de
EXEMPLO 1
∫
−
+
4
0
212
1 dxx /
)(

¨  Suponha x0 < x1 < ... < xn, (n + 1) pontos distintos em [x0, xn]
e que . Então, para cada x em [x0, xn], existe
um número ξ (x) (geralmente desconhecido) em ] x0, xn[, tal
que:
f ∈ Cn+1
a,b[ ]
R x( )= f x( )− Pn x( )=
f
n+1( )
ξ x( )( )
n +1( )!
x − x0( ) x − x1( )! x − xn( )
Erro da Regra dos Trapézios

¨  Erro da Regra dos Trapézios simples
¤  Da interpolação polinomial, temos que:
¤  Logo:
f x( )= p1 x( )+ x − x0( ) x − x1( )
f " ξx( )
2
, ξx ∈ x0, x1] [
f x( )dx
x0
x1
∫ = IT + x − x0( )
x0
x1
∫ x − x1( )
f " ξx( )
2
dx

¨  Então, temos que:
ET = x − x0( )
x0
x1
∫ x − x1( )
f " ξx( )
2
dx

¨  Já que (x – x0)(x - x1) não muda de sinal em [x0 , x1], o
Teorema do Valor Médio com Peso para Integrais pode
ser aplicado ao termo de erro, para algum :
¤  Então:
x − x0( )
x0
x1
∫ x − x1( ) f " ξx( )dx = f " c( ) x − x0( )
x0
x1
∫ x − x1( )dx
c ∈ x0, x1] [
ET =
f " c( )
2
x − x0( )
x0
x1
∫ x − x1( )dx

¨ 
¨  Como não podemos determinar exatamente c, temos:
ET = −
h3
12
f " c( ), c ∈ x0, x1] [
ET ≤
h3
12
M2
onde: M2 = máx
x∈[a,b]
f " x( )

¨ 
¤  O erro para cada um dos trapézios é dado por:
¤  Logo o erro da Regra dos Trapézios Repetida será a soma:
ET = −
h3
12
f " c( ), c ∈ x0, x1] [
ETR = −
h3
12
f " ci( )
i=0
n−1
∑ , ci ∈ xi, xi+1] [

¨ 
¨  Como estamos supondo f”(x) contínua em [a, b], uma
generalização do Teorema do Valor Intermediário nos
garante que existe tal que:
¨  Então:
ξ ∈ a,b] [
f " ci( )
i=0
n−1
∑ = n f " ξ( )
ETR = −
nh3
f " ξ( )
12
, ξ ∈ a,b] [

¨  Da mesma forma que na Interpolação Polinomial, não
podemos calcular exatamente f”(ξ), visto que não
conhecemos o ponto ξ. Quando possível, calculamos um
.
ETR ≤
nh3
12
M2
onde:
M2 = máx
x∈[a,b]
f " x( ) e h =
b− a
n

¨  Seja:
Calcule uma aproximação para I usando 10 subintervalos para
Regra dos Trapézios Composta. Estime o erro cometido.
EXEMPLO 2
∫=
1
0
dxeI x
[0,1] subdivididos em 10 subintervalos com h = 0,1
I = ex
dx
0
1
∫ ≈1,719713
f (x)dx ≈
h
2
f (x0 )+ 2 f (x1)+ f (x2 )+...+ f (xn−1)[ ]+ f (xn ){ }
x0
xn
∫

EXEMPLO 2
¨  O erro pela Regra dos Trapézios Repetida é:
¨  Portanto:
ETR ≤
nh3
12
máx
x∈[0,1]
ex
ETR ≤
0,01
12
máx
x∈[0,1]
ex
≈ 0,00227
e1

Regra
1/3 de Simpson

Regra 1/3 de Simpson
¨  Novamente podemos usar a para
estabelecer a fórmula de integração resultante da
aproximação de f (x) por um .

P2 x( )=
x − x1( ) x − x2( )
x0 − x1( ) x0 − x2( )
f x0( )+
x − x0( ) x − x2( )
x1 − x0( ) x1 − x2( )
f x1( )
+
x − x0( ) x − x1( )
x2 − x0( ) x2 − x1( )
f x2( )
IS = P2 x( )
x0
x2
∫ =
f x0( )
2h2
x − x1( ) x − x2( )dx
x0
x2
∫
−
f x1( )
h2
x − x0( ) x − x2( )dx
x0
x2
∫
+
f x2( )
2h2
x − x0( ) x − x1( )dx
x0
x2
∫

¨  As integrais podem ser resolvidas usando a mudança de
variáveis: x – x0 = zh. Assim: dx = h dz; x = x0 + zh;
¨  x – x1 = (z – 1) h; x – x2 = (z – 2) h.
¨  Fazendo esta mudança e resolvendo as integrais, obtemos a
:
f (x)dx ≈ IS =
h
3
f (x0 )+ 4 f (x1)+ f (x2 )[ ]
x0
x2
∫

Regra 1/3 de Simpson Repetida
¨  Da mesma forma que a Regra dos Trapézios Repetida,
aplicaremos a regra de Simpson repetidas vezes no intervalo
[a, b] = [x0 , xn].
¨  Então vamos supor subintervalos igualmente espaçados.

¨  Para cada teremos:
com k = 1, ..., n/2, sendo n um .
f (x)dx ≈ IS =
h
3
f (x2k−2 )+ 4 f (x2k−1)+ f (x2k )[ ]
x2k−2
x2k
∫

¨  Assim, a integral obtida pela regra de aproximação de
Simpson Repetida será dada por:
f (x)dx{ }
x0
xn
∫ ≈ ISR = h
3
f (x0 )+ f (xn )[ ]+{
+4 f (x1)+ f (x3)+!+ f (xn−1)[ ]+
+2 f (x2 )+ f (x4 )+!+ f (xn−2 )[ ]}
f (x)dx
x0
xn
∫ ≈ ISR =
h
3
f x0( )+ 2 f x2 j( )
j=1
n
2
−1
∑ + 4 f x2 j−1( )+ f xn( )
j=1
n
2
∑
%
&
'
'
'
(
)
*
*
*

¨  Supondo f (iv) (x) contínua em [x0 , x2]:
¨  O será:
ES = −
h5
90
f
iv( )
ξ( ), ξ ∈ x0, x2] [

¨  e o
¤  Calcularemos um para o erro:
onde:
M4 = máx
x∈[x0,xn ]
f
iv( )
x( ) e h =
b− a
n
ESR = −
n
2
h5
90
f
iv( )
ξ( ), ξ ∈ x0, xn] [
ESR ≤
nh5
180
M4

¨  Seja
Calcule uma aproximação para I usando a regra 1/3 de Simpson
com n = 10. Estime o erro cometido.
EXEMPLO 3
I = ex
dx
0
1
∫
[0,1] subdivididos em 10 subintervalos com h = 0,1
I = ex
dx
0
1
∫ ≈1,71828278
f (x)dx
x0
xn
∫ ≈ ISR =
h
3
f x0( )+ 2 f x2 j( )
j=1
n
2
−1
∑ + 4 f x2 j−1( )+ f xn( )
j=1
n
2
∑
%
&
'
'
'
(
)
*
*
*

Estimativa do erro cometido:
Exemplo 3
ESR = 5
0,1( )
5
90
eξ
, ξ ∈ ]0,1[
Portanto:
ESR ≤ 5,555×10−7
× máx
x∈[0,1]
ex
≈1,51016×10−6
e1

Comparação Exemplo 2 e 3
¨  Vamos comparar os resultados obtidos pela Regra dos
Trapézios e pela Regra 1/3 de Simpson.
¤  Regra dos Trapézios Repetida (n = 10):
¤  Regra 1/3 de Simpson Repetida (n = 10):
ex
dx
0
1
∫ ≈1,719713 ETR ≤ 2,27×10−3
ex
dx
0
1
∫ ≈1,71828278 ESR ≤1,51×10−6

Exemplo 4
¨  Considerando a integral dos exemplos 2 e 3.
a) Para quantas subdivisões do intervalo de integração (n)
teríamos erro inferior a 10-3 usando a Regra dos Trapézios?
b) E para a Regra 1/3 de Simpson?

Exemplo 4
a) Precisaremos de no mínimo 16 subdivisões do intervalo de
integração.
b) Precisaremos de no mínimo 2 subdivisões do intervalo de
integração.

Referências
¨  BURDEN, Richard L.; FAIRES, J. Douglas. Análise numérica.
São Paulo, SP: Cengage Learning, 2008. xiii, 721 p. ISBN
8522106010.
¨  RUGGIERO, Marcia A. Gomes; LOPES, Vera Lucia da Rocha.
Cálculo numérico: aspectos teóricos e computacionais. 2. ed. São
Paulo, SP: Makron, c1997. xvi, 406 p. ISBN 8534602042.
¨  CHAPRA, Steven C.; CANALE, Raymond P. Métodos numéricos
para engenharia. 5. ed. São Paulo: McGraw-Hill, 2008. 809 p.
ISBN 978-85-86804-87-8.

Cálculo Numérico - Integração Numérica

Recomendados

Recomendados

Mais conteúdo relacionado

Mais procurados

Mais procurados (20)

Semelhante a Cálculo Numérico - Integração Numérica

Semelhante a Cálculo Numérico - Integração Numérica (20)

Mais de Eder Ribeiro

Mais de Eder Ribeiro (10)

Cálculo Numérico - Integração Numérica